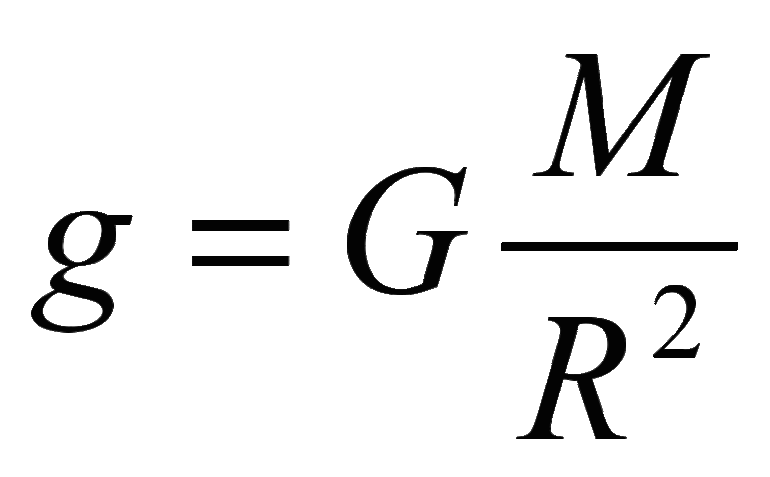Как пишется ускорение свободного падения в физике

Что такое свободное падение? Это падение тел на Землю при отсутствии сопротивления воздуха. Иначе говоря — падение в пустоте. Конечно, отсутствие сопротивления воздуха — это вакуум, который нельзя встретить на Земле в нормальных условиях. Поэтому мы не будем брать силу сопротивления воздуха во внимание, считая ее настолько малой, что ей можно пренебречь.

Ускорение свободного падения

Проводя свои знаменитые опыты на Пизанской башне Галилео Галилей выяснил, что все тела, независимо от их массы, падают на Землю одинаково. То есть, для всех тел ускорение свободного падения одинаково. По легенде, ученый тогда сбрасывал с башни шары разной массы.

Свободное падение тела

Рассмотрим простой пример свободного падения. Пусть некоторое тело падает с высоты h с нулевой начальной скоростью. Допустим мы подняли рояль на высоту h и спокойно отпустили его. 

Свободное падение — прямолинейное движение с постоянным ускорением. Направим ось координат от точки начального положения тела к Земле. Применяя формулы кинематики для прямолинейного равноускоренного движения, можно записать.

h=v0+gt22.

Так как начальна скорость равна нулю, перепишем:

h=gt22.

Отсюда находится выражение для времени падения тела с высоты h:

t=2hg.

Принимая во внимание, что v=gt, найдем скорость тела в момент падения, то есть максимальную скорость:

v=2hg·g=2hg.

Движение тела, брошенного вертикально вверх

Аналогично можно рассмотреть движение тела, брошенного вертикально вверх с определенной начальной скоростью. Например, мы бросаем вверх мячик.

Пусть ось координат направлена вертикально вверх из точки бросания тела. На сей раз тело движется равнозамедленно, теряя скорость. В наивысшей точки скорость тела равна нулю. Применяя формулы кинематики, можно записать:

v=v0-gt.

Подставив v=0, найдем время подъема тела на максимальную высоту:

t=v0g.

Время падения совпадает со временем подъема, и тело вернется на Землю через t=2v0g.

 Максимальная высота подъема тела, брошенного вертикально:

h=v022g.

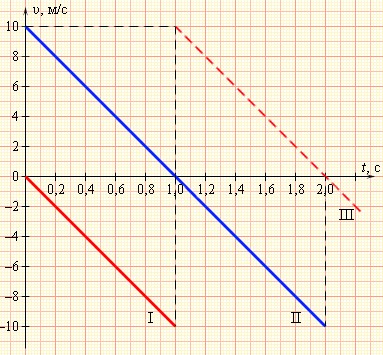
Взглянем на рисунок ниже. На нем приведены графики скоростей тел для трех случаев движения с ускорением a=-g. Рассмотрим каждый из них, предварительно уточнив, что в данном примере все числа округлены, а ускорение свободного падения принято равным 10мс2.

Первый график — это падение тела с некоторой высоты без начальной скорости. Время падения tп=1с. Из формул и из графика легко получить, что высота, с которой падало тело, равна h=5м.

Второй график — движение тела, брошенного вертикально вверх с начальной скоростью v0=10 мс. Максимальная высота подъема h=5м. Время подъема и время падения tп=1с.

Третий график является продолжением первого. Падающее тело отскакивает от поверхности и его скорость резко меняет знак на противоположный. Дальнейшее движение тела можно рассматривать по второму графику.

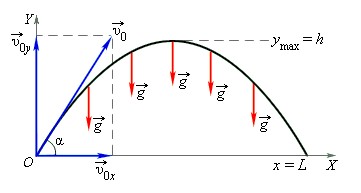
Движение тела, брошенного под углом к горизонту

С задачей о свободном падении тела тесно связана задача о движении тела, брошенного под определенным углом к горизонту. Так, движение по параболической траектории можно представить как сумму двух независимых движений относительно вертикальной и горизонтальной осей.

Вдоль оси OY тело движется равноускоренно с ускорением g, начальная скорость этого движения — v0y. Движение вдоль оси OX — равномерное и прямолинейное, с начальной скоростью v0x.

Условия для движения вдоль оси ОХ:

x0=0; v0x=v0cosα; ax=0.

Условия для движения вдоль оси OY:

y0=0; v0y=v0sinα; ay=-g.

Приведем формулы для движения тела, брошенного под углом к горизонту.

Время полета тела:

t=2v0sinαg.

Дальность полета тела:

L=v02sin2αg.

Максимальная дальность полета достигается при угле α=45°.

Lmax=v02g.

Максимальная высота подъема:

h=v02sin2α2g.

Отметим, что в реальных условиях движение тела, брошенного под углом к горизонту, может проходить по траектории, отличной от параболической вследствие сопротивления воздуха и ветра. Изучением движения тел, брошенных в пространстве, занимается специальная наука — баллистика.

Ускорение свободного падения

Ускорение свободного падения — движение объекта, который получает ускорение из-за действующей на него силы тяжести; обозначается буквой g и измеряется в м/с². На поверхности Земли ускорение свободного падения примерно равно 9,81 м/с².

На полюсах (Южном и Северном) ускорение свободного падения будет больше, а на экваторе — меньше. Это происходит из-за двух фактов:

• Земля — не идеальный круг, а приплюснутый шар и её радиус на полюсах меньше, чем на экваторе (ускорение зависит от радиуса),
• центробежные силы (при вращении Земли) минимально компенсируют гравитацию больше на экваторе, чем на полюсах.

В вакууме тела падают с одинаковой скоростью потому, что ускорение свободного падения не зависит от массы.

Таблица ускорения свободного падения небесных тел

Небесное тело	g (в м/с²)
Луна	1,62
Солнце	274
Меркурий	3,72
Венера	8,87
Земля	9,81
Марс	3,711
Юпитер	24,79
Сатурн	10,44
Уран	8,87
Нептун	11,15

От чего зависит ускорение свободного падения?

Ускорение свободного падения зависит от массы планеты и радиуса планеты — чем она тяжелее, тем сильнее притягивает тела (т.е. масса тела не влияет на ускорение).

Возможно для будущих вычислений нужны будут эти данные:

1. Масса Земли = 5,98 × (10^24) кг (или 5,972E24 кг)
2. Радиус Земли = 6 371 км = 6,37×(10^6) м.

Как найти ускорение свободного падения?

Формула ускорения свободного падения

Гравитационная постоянная («G», не путайте с «g») — это фундаментальная физическая константа, которая примерно равна

и связывает силы гравитационного притяжения между двумя телами (G) с их массами (m1 и m2) и расстоянием между ними (R) в формуле:

Пример расчёта ускорения свободного падения (для Земли):

Вспомним формулу:

Как узнать время падения тела?

Формула времени свободного падения (когда тело падает вертикально):

t = V / g = √(2h/g)

Где:

• t — время
• V — скорость тела
• g — ускорение ≈ 9,8 м/с²
• h — расстояние

Пример:

Высота (h) = 20 м

Нужно найти скорость и время падения.

Решение:

Формула скорости:

V0 = 0

g ≈ 9,8 м/с²

h = 20 м

V² = 0² + 2 × 9,8 м/с² × 20 м ⇔ V = √392 м/с ≈ 19,8 м/с

Зная скорость, применяем эту формулу:

t = V / g = (19,8 м/с) / (9,8 м/с²) ≈ 2,02 с

Либо используя только высоту и ускорение:

t = √(2h/g) = √(2 × 20 м / 9,8 м/с²) ≈ 2,02 с

Где нужны знания о свободном падении?

Они могут понадобиться:

• в авиации,
• в космонавтике,
• при поиске полезных ископаемых (там, где есть залежи тяжёлых ископаемых, g меняется),
• при разработке новых лыжных трамплинов и полос приземления,
• при разработке новых автомобилей (рассчитываются наилучшие показатели для экономии топлива).

Узнайте также про Закон сохранения энергии, Силу Архимеда, Законы Ньютона и Космологию.

Выберем тело, например, камень. Расположим его не некотором расстоянии от поверхности земли. Расстояние от центра Земли до камня равно ( R = left( r + h right) ), как представлено на рисунке 1.

Пусть на камень действует только сила, с которой Земля притягивает его, а других сил нет (нет, например, силы сопротивления воздуха).

Свободное падение – это движение тела под действием только одной силы — силы притяжения.

Из законов Ньютона известно: если на тело действует сила, то тело получает ускорение.

Ускорение свободного падения – это ускорение, с которым движется тело, когда на него действует только сила тяжести.

Формула для расчета ускорения свободного падения

Ускорение свободного падения можно посчитать по формуле:

[ large boxed { g = G cdot frac{M}{left( r + h right)^{2}} }]

( g left( frac{text{м}}{c^{2}} right) ) (метры, деленные на секунду в квадрате) – ускорение свободного падения

( M left( text{кг} right) ) (килограммы) — масса планеты, которая притягивает

( r left( text{м} right) ) (метры) – радиус планеты

( h left( text{м} right) ) (метры) — расстояние от поверхности планеты до тела

(G = 6{,}67 cdot 10^{-11} left( text{Н} cdot frac{text{м}^2}{text{кг}^2} right)) — гравитационная постоянная

Интересные факты

У разных планет ускорение свободного падения различается.

• чем больше масса планеты (или звезды), тем больше будет ускорение свободного падения рядом с такой планетой (или звездой);
• чем дальше от планеты, тем меньше ускорение свободного падения;
• на полюсах ускорение свободного падения больше, чем на экваторе планеты;

Важно!

Все тела под действием силы тяжести падают с одинаковым ускорением! Это ускорение не зависит от массы тела.

Из житейского опыта мы знаем: чем больше площадь тела, тем больше времени ему нужно, чтобы упасть с какой-либо высоты. При своем падении тело опирается на воздух, поэтому, к примеру, лист бумаги будет падать дольше, чем шарик из пластилина, или гирька.

В безвоздушном пространстве опираться не на что. Поэтому гирька, лист бумаги, птичье перо и пластилиновый шарик, стартовав с одной и той же высоты одновременно, упадут на поверхность планеты тоже одновременно.

Ускорение свободного падения у поверхности некоторых небесных тел

• у поверхности Земли  ( g = 9{,}8 left( frac{text{м}}{c^{2}} right) )
• у поверхности Луны  ( g = 1{,}68 left( frac{text{м}}{c^{2}} right) )
• у поверхности Марса  ( g = 3{,}86 left( frac{text{м}}{c^{2}} right) )
• у поверхности Солнца  ( g = 273{,}1 left( frac{text{м}}{c^{2}} right) )
• у поверхности Юпитера  ( g = 23{,}95 left( frac{text{м}}{c^{2}} right) )

Как вывести формулу ускорения свободного падения

Рассмотрим камень, находящийся на некотором расстоянии от Земли.

Земля и камень притягиваются, запишем закон притяжения между планетой и камнем

[  F = G cdot frac{mcdot M}{left( r + h right)^{2}} ]

С другой стороны, у камня есть вес, так как на него действует сила тяжести.

[  F_{text{тяж}} = m cdot g ]

Мы можем записать эти уравнения в виде системы.

[  begin{cases} displaystyle F = G cdot frac{mcdot M}{( r + h)^{2}} \ displaystyle  F_{text{тяж}} = m cdot g  end{cases} ]

Земля и камень притягиваются, благодаря этому на камень действует сила тяжести. На языке математики это запишется так:

[  F = F_{text{тяж}} ]

А если равны левые части уравнений, то будут равны и правые:

[  G cdot frac{mcdot M}{left( r + h right)^{2}} = m cdot g ]

Масса ( m ) камня встречается в обеих частях уравнения. Поделим обе части уравнения на массу камня.

[  G cdot frac{M}{ left( r + h right)^{2}} = g ]

Все)

Вам будет интересно почитать:

Закон всемирного тяготения

Законы Ньютона

Первая космическая скорость

Вторая космическая скорость

История открытия

Учёные Древней Греции разделяли любое движение на два типа: естественное и принудительное. Перемещение тела под воздействием гравитации считалось естественным, так как не имело видимой причины и происходило само собой.

Аристотель считал, что скорость падения напрямую зависит от массы. Это ошибочное утверждение родилось в результате примитивных наблюдений. Философ приводил в пример движение к земле яблок и листьев. Очевидно, что последние летели гораздо медленнее. Исследователи тех времён ещё очень мало понимали в физике. Такие понятия, как сопротивление воздуха и ускорение были неизвестны.

Утверждения Аристотеля считались неоспоримым постулатом вплоть до начала XVII века. Галилео Галлилей решительно отверг древнюю классификацию движения. В результате проведения нескольких опытов с движением тела по наклонной плоскости, учёный ввёл понятие ускорения.

Определение ускорения свободного падения в физике

Основное внимание Галлилей уделял изучению процесса свободного падения. Самым знаменитым стал эксперимент, проведённый на Пизанской башне.

С сооружения высотой 60-м были одновременно сброшены два предмета:

• маленький металлический шарик весом в пол фунта;
• большая круглая бомба, весившая 100 фунтов.

Результат был просто ошеломляющим. Оба тела достигли земли практически одновременно, а небольшая разница была объяснена силой сопротивления воздушной среды. Надо заметить, что наука тех лет существенно отличалась от сегодняшней. Считалось, что воздух не мешает падению, а, напротив, увеличивает его скорость.

Ещё одним заблуждением того времени было утверждение о том, что любое движение со временем прекращается, даже если на его пути нет преград. Галлилей опроверг и этот ошибочный закон физики, введя определение инерции.

В XVI веке ещё не существовало точных хронометров. Из-за этого ускорение падения тел с Пизанской башни было рассчитано довольно грубо. Для более точного измерения учёный изучал равноускоренное движение шарика по наклонной плоскости. А более или менее правильное значение ускорения сумел вычислить Гюйгенс в 1660 г.

Физическая сущность

Свободным падением может называться равноускоренное движение тела в результате действующей на него силы тяжести, происходящее в вакууме. Атмосфера Земли способна тормозить ускорение и замедлять падающие предметы. Однако, если величина сопротивления воздуха небольшая, ей можно пренебречь. К примеру, в опыте Галилея на башне в Пизе использовались шарообразные предметы, обладающие аэродинамичной формой. В результате этого коэффициент торможения удалось свести к минимуму.

Ускорение у поверхности Земли не зависит от массы предмета — это постоянная величина, обозначающаяся латинской буквой g и составляющая 9,80665 м/с.^2. Из-за воздействия центробежных сил на экваторе его значение немного меньше, а на полюсах, соответственно, больше.

Величина ускорения свободного падения зависит от нескольких факторов:

• географических координат, точнее, широты;
• расстояния до поверхности планеты;
• времени суток;
• геомагнитных аномалий.

Вектор свободного падения всегда направлен вниз. Это можно наглядно увидеть, подбросив какой-либо предмет. Благодаря воздействию ускорения, его движение будет постепенно замедляться. Затем оно полностью остановится и направится в обратную сторону.

Формулы для расчёта

Галилей понимал, что исследование падения тел с Пизанской башни является несовершенным. Был поставлен новый эксперимент, в котором учёному удалось увеличить время движения и уменьшить сопротивление воздуха. Отполированные латунные шарики скатывались по желобам, расположенным под определённым углом наклона. В результате были выведен физический закон, согласно которому все падающие тела движутся с одинаковой, постоянно увеличивающейся скоростью.

Формула для нахождения: g=G (M/R ^ 2), где:

• G — гравитационная постоянная;
• M — масса планеты;
• R — радиус планеты.

При помощи этой зависимости можно рассчитать значение g на поверхности любой планеты во вселенной.

Существуют задачи, для решения которых необходим более точный расчёт. В таком случае используется другая, расширенная формула: g=G (M/(R2+h)), ​где h — это высота над поверхностью планеты.

Стоит помнить, что для максимальной точности расчётов придётся учитывать большое количество факторов. Ускорение может измеряться при помощи специального прибора — гравиметра.

Ускорение на других планетах

Как видно из формулы, гравитационное ускорение напрямую зависит от массы и радиуса планеты. Из этого следует, что значение g на других планетах будет отличаться от земного.

Таблица показателя ускорения g для основных объектов Солнечной системы.

Наименование	Ускорение, м/с. 2
Солнце	274,01
Венера	8,87
Земля	9,81
Марс	3,72
Юпитер	25,8
Сатурн	11,54
Уран	9,04
Меркурий	3,73
Нептун	11,33
Луна	1,69

Солнце является самым большим объектом в солнечной системе, его масса почти в 300 тыс. раз больше земной. Но как можно заметить из таблицы, ускорение на поверхности звезды превышает земное всего в 28 раз. Это объясняется огромным радиусом светила.

Во вселенной существуют очень компактные объекты с невероятной плотностью и чудовищным притяжением. Если взять среднюю нейтронную звезду с радиусом 13 км и массой 2,5*10 ³⁰ кг, то ускорение на её поверхности превысит земное в 100 млрд раз и составит довольно внушительное число — 9,87*10^11м/с.²

Воздействие перегрузок на человека

Благодаря научно-техническому прогрессу и стремительному развитию технологий, современный человек имеет возможность пользоваться довольно быстрыми средствами передвижения. Чтобы попасть в любую точку планеты на самолёте, потребуется не более суток. Быстрая скорость передвижения неминуемо связана с таким понятием, как перегрузка.

Любая перегрузка являет собой отношение двух ускорений:

• негравитационного;
• свободного падения.

За единицу измерения принято брать гравитационное ускорение на Земле — 9,80665 м/с². Таким образом, нулевую перегрузку можно ощутить на себе лишь в невесомости.

Перегрузка является векторной величиной. Для людей и других живых организмов огромное значение имеет её направление. Это связано с тем, что организм приспособлен к постоянному воздействию гравитационного ускорения.

Характер положительной перегрузки заключается в том, что её вектор направлен вниз — от головы к ногам. Кровь оттекает от мозга и при показателе более 10 g человек может потерять сознание за считаные секунды. При отрицательном значении кровь, напротив, бьёт в голову. Это переносится гораздо хуже и может привести к кровоизлиянию и смерти.

Показатель перегрузки для различных ситуаций:

Пример	Показатель, g
Статичное положение,	1
Взлёт пассажирского авиалайнера	1,5
Приземление на парашюте	1,8
Раскрытие купола	10−16
Спуск космического аппарата «Союз»	3−4
Высший пилотаж на спортивном самолёте	от -7 до +12
Максимальная длительная перегрузка, переносимая человеком	8−10
Аварийный спуск из космоса	20−26
Рекордная не смертельная перегрузка при автокатастрофе	214
Торможение автоматического аппарата в атмосфере Венеры	350
Предел прочности твердотельного накопителя информации	1500
Снаряд в момент выстрела	47 тыс.

Военным и спортивным лётчикам приходится постоянно испытывать большие перегрузки. Для уменьшения вредного воздействия на организм существуют специальные защитные костюмы.

Переносить перегрузку лучше всего лёжа на спине. Именно в таком положении находятся космонавты при взлёте ракет.

>