| Acceleration | |
|---|---|

In vacuum (no air resistance), objects attracted by Earth gain speed at a steady rate. |
|
|
Common symbols |
a |
| SI unit | m/s2, m·s−2, m s−2 |
|
Derivations from |
 |
| Dimension |  |
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities (in that they have magnitude and direction).[1][2] The orientation of an object’s acceleration is given by the orientation of the net force acting on that object. The magnitude of an object’s acceleration, as described by Newton’s Second Law,[3] is the combined effect of two causes:
- the net balance of all external forces acting onto that object — magnitude is directly proportional to this net resulting force;
- that object’s mass, depending on the materials out of which it is made — magnitude is inversely proportional to the object’s mass.
The SI unit for acceleration is metre per second squared (m⋅s−2, 
For example, when a vehicle starts from a standstill (zero velocity, in an inertial frame of reference) and travels in a straight line at increasing speeds, it is accelerating in the direction of travel. If the vehicle turns, an acceleration occurs toward the new direction and changes its motion vector. The acceleration of the vehicle in its current direction of motion is called a linear (or tangential during circular motions) acceleration, the reaction to which the passengers on board experience as a force pushing them back into their seats. When changing direction, the effecting acceleration is called radial (or centripetal during circular motions) acceleration, the reaction to which the passengers experience as a centrifugal force. If the speed of the vehicle decreases, this is an acceleration in the opposite direction and mathematically a negative, sometimes called deceleration or retardation, and passengers experience the reaction to deceleration as an inertial force pushing them forward. Such negative accelerations are often achieved by retrorocket burning in spacecraft.[4] Both acceleration and deceleration are treated the same, as they are both changes in velocity. Each of these accelerations (tangential, radial, deceleration) is felt by passengers until their relative (differential) velocity are neutralized in reference to the acceleration due to change in speed.
Definition and properties[edit]
Kinematic quantities of a classical particle: mass m, position r, velocity v, acceleration a.
Average acceleration[edit]
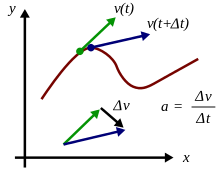
Acceleration is the rate of change of velocity. At any point on a trajectory, the magnitude of the acceleration is given by the rate of change of velocity in both magnitude and direction at that point. The true acceleration at time t is found in the limit as time interval Δt → 0 of Δv/Δt
An object’s average acceleration over a period of time is its change in velocity, 

Instantaneous acceleration[edit]
From bottom to top:
- an acceleration function a(t);
- the integral of the acceleration is the velocity function v(t);
- and the integral of the velocity is the distance function s(t).
Instantaneous acceleration, meanwhile, is the limit of the average acceleration over an infinitesimal interval of time. In the terms of calculus, instantaneous acceleration is the derivative of the velocity vector with respect to time:
As acceleration is defined as the derivative of velocity, v, with respect to time t and velocity is defined as the derivative of position, x, with respect to time, acceleration can be thought of as the second derivative of x with respect to t:
(Here and elsewhere, if motion is in a straight line, vector quantities can be substituted by scalars in the equations.)
By the fundamental theorem of calculus, it can be seen that the integral of the acceleration function a(t) is the velocity function v(t); that is, the area under the curve of an acceleration vs. time (a vs. t) graph corresponds to the change of velocity.

Likewise, the integral of the jerk function j(t), the derivative of the acceleration function, can be used to find the change of acceleration at a certain time:
Units[edit]
Acceleration has the dimensions of velocity (L/T) divided by time, i.e. L T−2. The SI unit of acceleration is the metre per second squared (m s−2); or «metre per second per second», as the velocity in metres per second changes by the acceleration value, every second.
Other forms[edit]
An object moving in a circular motion—such as a satellite orbiting the Earth—is accelerating due to the change of direction of motion, although its speed may be constant. In this case it is said to be undergoing centripetal (directed towards the center) acceleration.
Proper acceleration, the acceleration of a body relative to a free-fall condition, is measured by an instrument called an accelerometer.
In classical mechanics, for a body with constant mass, the (vector) acceleration of the body’s center of mass is proportional to the net force vector (i.e. sum of all forces) acting on it (Newton’s second law):

where F is the net force acting on the body, m is the mass of the body, and a is the center-of-mass acceleration. As speeds approach the speed of light, relativistic effects become increasingly large.
Tangential and centripetal acceleration[edit]
An oscillating pendulum, with velocity and acceleration marked. It experiences both tangential and centripetal acceleration.
Components of acceleration for a curved motion. The tangential component at is due to the change in speed of traversal, and points along the curve in the direction of the velocity vector (or in the opposite direction). The normal component (also called centripetal component for circular motion) ac is due to the change in direction of the velocity vector and is normal to the trajectory, pointing toward the center of curvature of the path.
The velocity of a particle moving on a curved path as a function of time can be written as:
with v(t) equal to the speed of travel along the path, and
a unit vector tangent to the path pointing in the direction of motion at the chosen moment in time. Taking into account both the changing speed v(t) and the changing direction of ut, the acceleration of a particle moving on a curved path can be written using the chain rule of differentiation[5] for the product of two functions of time as:
where un is the unit (inward) normal vector to the particle’s trajectory (also called the principal normal), and r is its instantaneous radius of curvature based upon the osculating circle at time t. These components are called the tangential acceleration and the normal or radial acceleration (or centripetal acceleration in circular motion, see also circular motion and centripetal force).
Geometrical analysis of three-dimensional space curves, which explains tangent, (principal) normal and binormal, is described by the Frenet–Serret formulas.[6][7]
Special cases[edit]
Uniform acceleration[edit]
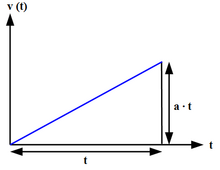
Calculation of the speed difference for a uniform acceleration
Uniform or constant acceleration is a type of motion in which the velocity of an object changes by an equal amount in every equal time period.
A frequently cited example of uniform acceleration is that of an object in free fall in a uniform gravitational field. The acceleration of a falling body in the absence of resistances to motion is dependent only on the gravitational field strength g (also called acceleration due to gravity). By Newton’s Second Law the force 
Because of the simple analytic properties of the case of constant acceleration, there are simple formulas relating the displacement, initial and time-dependent velocities, and acceleration to the time elapsed:[8]
where
In particular, the motion can be resolved into two orthogonal parts, one of constant velocity and the other according to the above equations. As Galileo showed, the net result is parabolic motion, which describes, e. g., the trajectory of a projectile in a vacuum near the surface of Earth.[9]
Circular motion[edit]
Position vector r, always points radially from the origin.
Velocity vector v, always tangent to the path of motion.
Acceleration vector a, not parallel to the radial motion but offset by the angular and Coriolis accelerations, nor tangent to the path but offset by the centripetal and radial accelerations.
Kinematic vectors in plane polar coordinates. Notice the setup is not restricted to 2d space, but may represent the osculating plane plane in a point of an arbitrary curve in any higher dimension.
In uniform circular motion, that is moving with constant speed along a circular path, a particle experiences an acceleration resulting from the change of the direction of the velocity vector, while its magnitude remains constant. The derivative of the location of a point on a curve with respect to time, i.e. its velocity, turns out to be always exactly tangential to the curve, respectively orthogonal to the radius in this point. Since in uniform motion the velocity in the tangential direction does not change, the acceleration must be in radial direction, pointing to the center of the circle. This acceleration constantly changes the direction of the velocity to be tangent in the neighboring point, thereby rotating the velocity vector along the circle.
Expressing centripetal acceleration vector in polar components, where 
As usual in rotations, the speed 


Thus 
This acceleration and the mass of the particle determine the necessary centripetal force, directed toward the centre of the circle, as the net force acting on this particle to keep it in this uniform circular motion. The so-called ‘centrifugal force’, appearing to act outward on the body, is a so-called pseudo force experienced in the frame of reference of the body in circular motion, due to the body’s linear momentum, a vector tangent to the circle of motion.
In a nonuniform circular motion, i.e., the speed along the curved path is changing, the acceleration has a non-zero component tangential to the curve, and is not confined to the principal normal, which directs to the center of the osculating circle, that determines the radius 




The sign of the tangential component of the acceleration is determined by the sign of the angular acceleration (
Relation to relativity[edit]
Special relativity[edit]
The special theory of relativity describes the behavior of objects traveling relative to other objects at speeds approaching that of light in a vacuum. Newtonian mechanics is exactly revealed to be an approximation to reality, valid to great accuracy at lower speeds. As the relevant speeds increase toward the speed of light, acceleration no longer follows classical equations.
As speeds approach that of light, the acceleration produced by a given force decreases, becoming infinitesimally small as light speed is approached; an object with mass can approach this speed asymptotically, but never reach it.
General relativity[edit]
Unless the state of motion of an object is known, it is impossible to distinguish whether an observed force is due to gravity or to acceleration—gravity and inertial acceleration have identical effects. Albert Einstein called this the equivalence principle, and said that only observers who feel no force at all—including the force of gravity—are justified in concluding that they are not accelerating.[10]
Conversions[edit]
| Base value | (Gal, or cm/s2) | (ft/s2) | (m/s2) | (Standard gravity, g0) |
|---|---|---|---|---|
| 1 Gal, or cm/s2 | 1 | 0.0328084 | 0.01 | 1.01972×10−3 |
| 1 ft/s2 | 30.4800 | 1 | 0.304800 | 0.0310810 |
| 1 m/s2 | 100 | 3.28084 | 1 | 0.101972 |
| 1 g0 | 980.665 | 32.1740 | 9.80665 | 1 |
See also[edit]
- Acceleration (differential geometry)
- Four-vector: making the connection between space and time explicit
- Gravitational acceleration
- Inertia
- Orders of magnitude (acceleration)
- Shock (mechanics)
- Shock and vibration data logger
measuring 3-axis acceleration - Space travel using constant acceleration
- Specific force
References[edit]
- ^ Bondi, Hermann (1980). Relativity and Common Sense. Courier Dover Publications. pp. 3. ISBN 978-0-486-24021-3.
- ^ Lehrman, Robert L. (1998). Physics the Easy Way. Barron’s Educational Series. pp. 27. ISBN 978-0-7641-0236-3.
- ^ Crew, Henry (2008). The Principles of Mechanics. BiblioBazaar, LLC. p. 43. ISBN 978-0-559-36871-4.
- ^ Raymond A. Serway; Chris Vuille; Jerry S. Faughn (2008). College Physics, Volume 10. Cengage. p. 32. ISBN 9780495386933.
- ^ Weisstein, Eric W. «Chain Rule». Wolfram MathWorld. Wolfram Research. Retrieved 2 August 2016.
- ^ Larry C. Andrews; Ronald L. Phillips (2003). Mathematical Techniques for Engineers and Scientists. SPIE Press. p. 164. ISBN 978-0-8194-4506-3.
- ^ Ch V Ramana Murthy; NC Srinivas (2001). Applied Mathematics. New Delhi: S. Chand & Co. p. 337. ISBN 978-81-219-2082-7.
- ^ Keith Johnson (2001). Physics for you: revised national curriculum edition for GCSE (4th ed.). Nelson Thornes. p. 135. ISBN 978-0-7487-6236-1.
- ^ David C. Cassidy; Gerald James Holton; F. James Rutherford (2002). Understanding physics. Birkhäuser. p. 146. ISBN 978-0-387-98756-9.
- ^ Brian Greene, The Fabric of the Cosmos: Space, Time, and the Texture of Reality, page 67. Vintage ISBN 0-375-72720-5
External links[edit]
- Acceleration Calculator Simple acceleration unit converter
- Acceleration Calculator Acceleration Conversion calculator converts units form meter per second square, kilometer per second square, millimeter per second square & more with metric conversion.
| Acceleration | |
|---|---|

In vacuum (no air resistance), objects attracted by Earth gain speed at a steady rate. |
|
|
Common symbols |
a |
| SI unit | m/s2, m·s−2, m s−2 |
|
Derivations from |
 |
| Dimension |  |
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities (in that they have magnitude and direction).[1][2] The orientation of an object’s acceleration is given by the orientation of the net force acting on that object. The magnitude of an object’s acceleration, as described by Newton’s Second Law,[3] is the combined effect of two causes:
- the net balance of all external forces acting onto that object — magnitude is directly proportional to this net resulting force;
- that object’s mass, depending on the materials out of which it is made — magnitude is inversely proportional to the object’s mass.
The SI unit for acceleration is metre per second squared (m⋅s−2, 
For example, when a vehicle starts from a standstill (zero velocity, in an inertial frame of reference) and travels in a straight line at increasing speeds, it is accelerating in the direction of travel. If the vehicle turns, an acceleration occurs toward the new direction and changes its motion vector. The acceleration of the vehicle in its current direction of motion is called a linear (or tangential during circular motions) acceleration, the reaction to which the passengers on board experience as a force pushing them back into their seats. When changing direction, the effecting acceleration is called radial (or centripetal during circular motions) acceleration, the reaction to which the passengers experience as a centrifugal force. If the speed of the vehicle decreases, this is an acceleration in the opposite direction and mathematically a negative, sometimes called deceleration or retardation, and passengers experience the reaction to deceleration as an inertial force pushing them forward. Such negative accelerations are often achieved by retrorocket burning in spacecraft.[4] Both acceleration and deceleration are treated the same, as they are both changes in velocity. Each of these accelerations (tangential, radial, deceleration) is felt by passengers until their relative (differential) velocity are neutralized in reference to the acceleration due to change in speed.
Definition and properties[edit]
Kinematic quantities of a classical particle: mass m, position r, velocity v, acceleration a.
Average acceleration[edit]
Acceleration is the rate of change of velocity. At any point on a trajectory, the magnitude of the acceleration is given by the rate of change of velocity in both magnitude and direction at that point. The true acceleration at time t is found in the limit as time interval Δt → 0 of Δv/Δt
An object’s average acceleration over a period of time is its change in velocity, 

Instantaneous acceleration[edit]
From bottom to top:
- an acceleration function a(t);
- the integral of the acceleration is the velocity function v(t);
- and the integral of the velocity is the distance function s(t).
Instantaneous acceleration, meanwhile, is the limit of the average acceleration over an infinitesimal interval of time. In the terms of calculus, instantaneous acceleration is the derivative of the velocity vector with respect to time:
As acceleration is defined as the derivative of velocity, v, with respect to time t and velocity is defined as the derivative of position, x, with respect to time, acceleration can be thought of as the second derivative of x with respect to t:
(Here and elsewhere, if motion is in a straight line, vector quantities can be substituted by scalars in the equations.)
By the fundamental theorem of calculus, it can be seen that the integral of the acceleration function a(t) is the velocity function v(t); that is, the area under the curve of an acceleration vs. time (a vs. t) graph corresponds to the change of velocity.

Likewise, the integral of the jerk function j(t), the derivative of the acceleration function, can be used to find the change of acceleration at a certain time:
Units[edit]
Acceleration has the dimensions of velocity (L/T) divided by time, i.e. L T−2. The SI unit of acceleration is the metre per second squared (m s−2); or «metre per second per second», as the velocity in metres per second changes by the acceleration value, every second.
Other forms[edit]
An object moving in a circular motion—such as a satellite orbiting the Earth—is accelerating due to the change of direction of motion, although its speed may be constant. In this case it is said to be undergoing centripetal (directed towards the center) acceleration.
Proper acceleration, the acceleration of a body relative to a free-fall condition, is measured by an instrument called an accelerometer.
In classical mechanics, for a body with constant mass, the (vector) acceleration of the body’s center of mass is proportional to the net force vector (i.e. sum of all forces) acting on it (Newton’s second law):

where F is the net force acting on the body, m is the mass of the body, and a is the center-of-mass acceleration. As speeds approach the speed of light, relativistic effects become increasingly large.
Tangential and centripetal acceleration[edit]
An oscillating pendulum, with velocity and acceleration marked. It experiences both tangential and centripetal acceleration.
Components of acceleration for a curved motion. The tangential component at is due to the change in speed of traversal, and points along the curve in the direction of the velocity vector (or in the opposite direction). The normal component (also called centripetal component for circular motion) ac is due to the change in direction of the velocity vector and is normal to the trajectory, pointing toward the center of curvature of the path.
The velocity of a particle moving on a curved path as a function of time can be written as:
with v(t) equal to the speed of travel along the path, and
a unit vector tangent to the path pointing in the direction of motion at the chosen moment in time. Taking into account both the changing speed v(t) and the changing direction of ut, the acceleration of a particle moving on a curved path can be written using the chain rule of differentiation[5] for the product of two functions of time as:
where un is the unit (inward) normal vector to the particle’s trajectory (also called the principal normal), and r is its instantaneous radius of curvature based upon the osculating circle at time t. These components are called the tangential acceleration and the normal or radial acceleration (or centripetal acceleration in circular motion, see also circular motion and centripetal force).
Geometrical analysis of three-dimensional space curves, which explains tangent, (principal) normal and binormal, is described by the Frenet–Serret formulas.[6][7]
Special cases[edit]
Uniform acceleration[edit]
Calculation of the speed difference for a uniform acceleration
Uniform or constant acceleration is a type of motion in which the velocity of an object changes by an equal amount in every equal time period.
A frequently cited example of uniform acceleration is that of an object in free fall in a uniform gravitational field. The acceleration of a falling body in the absence of resistances to motion is dependent only on the gravitational field strength g (also called acceleration due to gravity). By Newton’s Second Law the force 
Because of the simple analytic properties of the case of constant acceleration, there are simple formulas relating the displacement, initial and time-dependent velocities, and acceleration to the time elapsed:[8]
where
In particular, the motion can be resolved into two orthogonal parts, one of constant velocity and the other according to the above equations. As Galileo showed, the net result is parabolic motion, which describes, e. g., the trajectory of a projectile in a vacuum near the surface of Earth.[9]
Circular motion[edit]
Position vector r, always points radially from the origin.
Velocity vector v, always tangent to the path of motion.
Acceleration vector a, not parallel to the radial motion but offset by the angular and Coriolis accelerations, nor tangent to the path but offset by the centripetal and radial accelerations.
Kinematic vectors in plane polar coordinates. Notice the setup is not restricted to 2d space, but may represent the osculating plane plane in a point of an arbitrary curve in any higher dimension.
In uniform circular motion, that is moving with constant speed along a circular path, a particle experiences an acceleration resulting from the change of the direction of the velocity vector, while its magnitude remains constant. The derivative of the location of a point on a curve with respect to time, i.e. its velocity, turns out to be always exactly tangential to the curve, respectively orthogonal to the radius in this point. Since in uniform motion the velocity in the tangential direction does not change, the acceleration must be in radial direction, pointing to the center of the circle. This acceleration constantly changes the direction of the velocity to be tangent in the neighboring point, thereby rotating the velocity vector along the circle.
Expressing centripetal acceleration vector in polar components, where 
As usual in rotations, the speed 


Thus 
This acceleration and the mass of the particle determine the necessary centripetal force, directed toward the centre of the circle, as the net force acting on this particle to keep it in this uniform circular motion. The so-called ‘centrifugal force’, appearing to act outward on the body, is a so-called pseudo force experienced in the frame of reference of the body in circular motion, due to the body’s linear momentum, a vector tangent to the circle of motion.
In a nonuniform circular motion, i.e., the speed along the curved path is changing, the acceleration has a non-zero component tangential to the curve, and is not confined to the principal normal, which directs to the center of the osculating circle, that determines the radius 




The sign of the tangential component of the acceleration is determined by the sign of the angular acceleration (
Relation to relativity[edit]
Special relativity[edit]
The special theory of relativity describes the behavior of objects traveling relative to other objects at speeds approaching that of light in a vacuum. Newtonian mechanics is exactly revealed to be an approximation to reality, valid to great accuracy at lower speeds. As the relevant speeds increase toward the speed of light, acceleration no longer follows classical equations.
As speeds approach that of light, the acceleration produced by a given force decreases, becoming infinitesimally small as light speed is approached; an object with mass can approach this speed asymptotically, but never reach it.
General relativity[edit]
Unless the state of motion of an object is known, it is impossible to distinguish whether an observed force is due to gravity or to acceleration—gravity and inertial acceleration have identical effects. Albert Einstein called this the equivalence principle, and said that only observers who feel no force at all—including the force of gravity—are justified in concluding that they are not accelerating.[10]
Conversions[edit]
| Base value | (Gal, or cm/s2) | (ft/s2) | (m/s2) | (Standard gravity, g0) |
|---|---|---|---|---|
| 1 Gal, or cm/s2 | 1 | 0.0328084 | 0.01 | 1.01972×10−3 |
| 1 ft/s2 | 30.4800 | 1 | 0.304800 | 0.0310810 |
| 1 m/s2 | 100 | 3.28084 | 1 | 0.101972 |
| 1 g0 | 980.665 | 32.1740 | 9.80665 | 1 |
See also[edit]
- Acceleration (differential geometry)
- Four-vector: making the connection between space and time explicit
- Gravitational acceleration
- Inertia
- Orders of magnitude (acceleration)
- Shock (mechanics)
- Shock and vibration data logger
measuring 3-axis acceleration - Space travel using constant acceleration
- Specific force
References[edit]
- ^ Bondi, Hermann (1980). Relativity and Common Sense. Courier Dover Publications. pp. 3. ISBN 978-0-486-24021-3.
- ^ Lehrman, Robert L. (1998). Physics the Easy Way. Barron’s Educational Series. pp. 27. ISBN 978-0-7641-0236-3.
- ^ Crew, Henry (2008). The Principles of Mechanics. BiblioBazaar, LLC. p. 43. ISBN 978-0-559-36871-4.
- ^ Raymond A. Serway; Chris Vuille; Jerry S. Faughn (2008). College Physics, Volume 10. Cengage. p. 32. ISBN 9780495386933.
- ^ Weisstein, Eric W. «Chain Rule». Wolfram MathWorld. Wolfram Research. Retrieved 2 August 2016.
- ^ Larry C. Andrews; Ronald L. Phillips (2003). Mathematical Techniques for Engineers and Scientists. SPIE Press. p. 164. ISBN 978-0-8194-4506-3.
- ^ Ch V Ramana Murthy; NC Srinivas (2001). Applied Mathematics. New Delhi: S. Chand & Co. p. 337. ISBN 978-81-219-2082-7.
- ^ Keith Johnson (2001). Physics for you: revised national curriculum edition for GCSE (4th ed.). Nelson Thornes. p. 135. ISBN 978-0-7487-6236-1.
- ^ David C. Cassidy; Gerald James Holton; F. James Rutherford (2002). Understanding physics. Birkhäuser. p. 146. ISBN 978-0-387-98756-9.
- ^ Brian Greene, The Fabric of the Cosmos: Space, Time, and the Texture of Reality, page 67. Vintage ISBN 0-375-72720-5
External links[edit]
- Acceleration Calculator Simple acceleration unit converter
- Acceleration Calculator Acceleration Conversion calculator converts units form meter per second square, kilometer per second square, millimeter per second square & more with metric conversion.
Как найти ускорение — определение и формулы расчета в физике
Содержание:
-
Что такое ускорение
- Единица измерения
-
Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
- Мгновенное ускорение
- Максимальное ускорение
- Среднее ускорение
- Проекция ускорения
Что такое ускорение
Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
Единица измерения
В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
(a;=;frac{mathrm V}t)
(a;=;frac{2S}{t^2})
(a;=;frac{V^2}{2S})
Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
или
(overrightarrow a=frac{overrightarrow F}m)
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})
Максимальное ускорение
(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.
Среднее ускорение
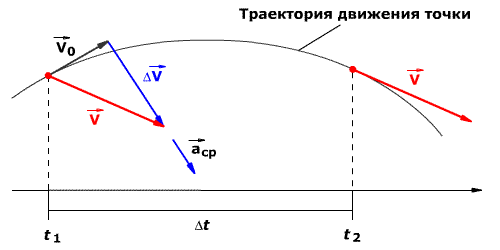
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.
Проекция ускорения
Определение проекции ускорения на ось (х):
(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.
Насколько полезной была для вас статья?
Рейтинг: 1.93 (Голосов: 30)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
В такой точной науке, как физика, важно знать правильные обозначения разных физических величин. Стандартные обозначения позволяют избежать многих ошибок при решении задач, а также способствуют запоминанию формул. Рассмотрим в статье, как обозначается в физике ускорение.
Определение ускорения
Какой буквой обозначается ускорение в физике? Ответить на этот вопрос нельзя однозначно, поскольку существуют различные типы ускорения, применяемые для разных видов движения и взаимодействия. Для начала приведем определение ускорения. Под ним понимают такую величину, которая отражает изменение скорости во времени. Математически принято это определение записывать следующим образом:
a¯ = dv¯/dt
То есть ускорение — это первая производная скорости по времени. Формула также демонстрирует, как обозначается ускорение в физике. Действительно, в общем случае его обозначают латинской буквой a¯, где черта указывает на то, что данная величина является векторной.
Ускорение также обозначается как a¯ во втором законе Ньютона:
F¯ = m*a¯
Тем не менее существуют специфические типы движения и виды взаимодействия, для которых используют свои символы для обозначения ускорения. Рассмотрим их.
Тангенциальное и нормальное ускорение
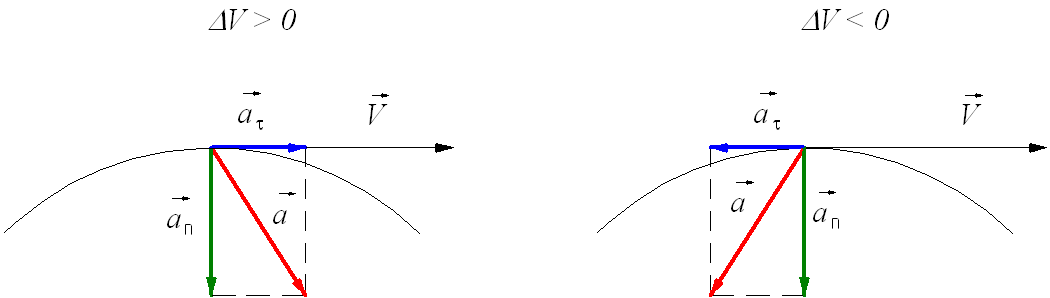
Каждый школьник, который знаком с понятием ускорения, знает, что в случае криволинейного перемещения оно может быть представлено в виде векторной суммы двух компонент: касательного и центростремительного ускорений. Первое описывает изменение модуля скорости и направлено по касательной к траектории перемещения тела, второе же появляется потому, что скорость меняет свое направление. Центростремительное ускорение, как свидетельствует его название, направлено к центру кривизны в данной точке траектории.
Как обозначаются в физике ускорения полного компоненты? Их принято обозначать также латинской буквой a, но с соответствующим нижним индексом t — тангенциальное или c — центростремительное. Вместо c также может быть использован индекс n — нормальное, поскольку оно направлено по нормали к касательной в точке траектории. Полное ускорение a через компоненты at и an рассчитывается так:
a = √(at2 + an2)
Угловое ускорение
Это специфический вид ускорения, который удобно использовать при решении кинематических и динамических уравнений вращательного движения тел и их систем. Согласно определению, угловое ускорение описывает быстроту изменения угловой скорости, то есть:
α¯ = dω¯/dt
Из формулы видно, как в физике обозначается ускорение угловое. Для него используют греческий аналог латинской буквы a, то есть букву α (альфа). Тем не менее в некоторых задачах можно встретить букву ε (эпсилон) для обозначения рассматриваемой величины.
Ускорение угловое можно связать только с линейным тангенциальным ускорением, что отражает приведенная ниже формула:
at = α*r
Здесь r — радиус окружности вращения. Эта формула означает, что величина α, так же как величина at, описывает абсолютное изменение скорости. Измеряется α в радианах в секунду квадратную (рад/с2).
Формулы связи между угловым и нормальным ускорением не существует ввиду различия в физическом смысле этих величин.
Ускорение под действием гравитационной силы
Каждый школьник знает, как рассчитывать силу тяжести или вес тела. Выполняются вычисления по такой формуле:
F = P = m*g
Здесь F и P — сила тяжести и вес тела соответственно. Величина g является ускорением свободного падения. Зная теперь, как обозначается ускорение свободного падения в физике, отметим, что латинская буква g была выбрана потому, что в латинском языке слово «гравитация» начинается с нее (gravitas). Кстати, буква a для полного и других видов ускорения была выбрана по той же причине (acceleratio с лат. означает «ускорение»).
Ускорение g в отличие от других рассмотренных видов ускорения является величиной постоянной для данной планеты вблизи ее поверхности. Например, для Земли g = 9,81 м/с2, для Луны — 1,62 м/с2, а для Марса — 3,711 м/с2. Эта величина прямо пропорциональна массе планеты и обратно пропорциональна квадрату ее радиуса.
Почему величину g не обозначают буквой a?
Разобравшись подробно с вопросом, как обозначается ускорение в физике, будет интересно также узнать ответ на вопрос данного пункта. Он более чем очевиден: g не обозначают буквой a потому, что она является константой в постоянном гравитационном поле. Более того, буква g отражает природу происхождения этого ускорения.
Что касается обозначения a, то оно отражает переменный характер механического движения. Причиной его появления может быть совершенно любая сила, кроме силы тяжести. Например, это сила мотора двигателя, который раскручивает колеса автомобиля, или сила натяжения нити, создающая центростремительное ускорения при вращении с телом на ее конце. Также это может быть сила трения или сила упругости.
Различные обозначения a и g удобно использовать при решении задач на подъем и падение тел. Например, в случае подъема ракеты или самолета оба ускорения используются для вычисления веса пилотов и пассажиров.
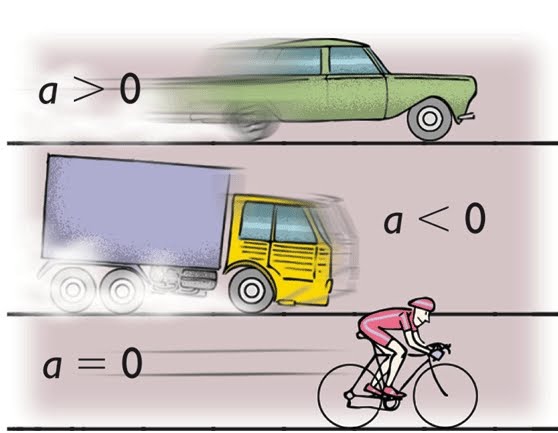
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
v2 > v1
а направление вектора ускорения совпадает с вектором скорости
Если скорость тела по модулю уменьшается, то есть
v2 < v1
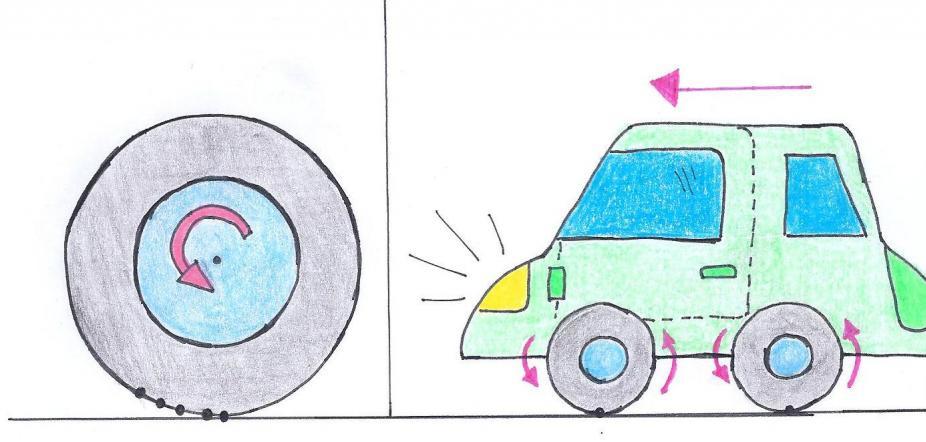
то направление вектора ускорения противоположно направлению вектора скорости Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
Среди прочих обозначений наиболее часто школьников интересует вопрос о том, как в математике обозначается скорость, время, расстояние. Связано это с тем, что обозначения этих величин (особенно — скорости) в учебниках по математике и физике можно увидеть различные: с чертой над буквой v (читается: [вэ]), со стрелкой над буквой v, а также буквы v, выделенные курсивом или жирным шрифтом.
Скорость в математике обозначается буквой v, но её написание принято различным для рукописного и печатного текста.
В рукописном тексте скорость движения обычно обозначается строчной (т.е. маленькой) прописной (т.е. не печатной, как в тексте из газеты, а написанной от руки так, как если бы писали письмо) буквой v. В учебниках по математике (т.е. в печатном тексте) обычно скорость движения обозначается печатной буквой v, прямой или выделенной курсивом. Такое обозначение принимается практически во всех задачах по математике, исключение составляют лишь задачи, иллюстрирующие тему «Векторы» (в этом случае обозначение принимается таким же, как и в физике).
В физике (а точнее – в её разделе «механика») обозначение скорости зависит от того, нужно ли в данной задаче учитывать тот факт, что скорость – величина векторная. Там, где учитывать это не нужно, скорость обозначается строчной буквой v (печатной или прописной, так же, как и в математике). Если же необходимо учитывать то, что скорость характеризуется не только модулем (т.е. величиной), но и направлением, скорость изображается либо прописной буквой v с направленной слева направо стрелкой над этой буквой, либо той же прописной буквой v с горизонтальной чертой над этой буквой. В печатном тексте в этом случае обычно скорость обозначают либо печатной строчной буквой v со стрелкой или чертой над буквой, либо печатной буквой v, выделенной жирным шрифтом (т.е. так: v).
Буквой v обозначают скорость движения тел. Для обозначения скорости света и скорости звука принята другая, отличная от обозначения скорости движения тел, буква. Скорость света обозначается буквой «с» (скорость света в вакууме составляет с = 2,9979х108 м/с = 2,9979х105 км/с). Скорость звука так же обозначается буквой с (читается: [цэ]).
Ускорение обозначается буквой а (исключение составляет лишь ускорение свободного падения, эта величина обозначается буквой g (читается [жэ]), g = 9,81 м/с2). Если необходимо подчеркнуть, что эта величина – векторная (например, это часто требуется в физике), то над буквой «а» изображается либо горизонтальная черта, либо горизонтальная стрелка (так же, как и при обозначении скорости). В печатном тексте для обозначения ускорения как векторной величины может использоваться и буква «а», выделенная жирным шрифтом.
Если при решении задачи по физике или математике необходимо обозначить время, то это пишется буквой так: t (читается: [тэ]), а если расстояние — пишется буквой так: s (читается: [эс]). Для обозначения пути обычно используется строчная (маленькая) буква [эль], т.е. l, реже — заглавная (большая) буква [эль], т.е. L. Чтобы обозначение пути «l» не было похоже на «единицу», эту букву пишут курсивом, т.е. с наклоном.
Вообще, вопросы «как в математике пишется скорость», «как в математике пишется время», «как в математике пишется расстояние» некорректны. Лучше формулировать такой вопрос, употребляя не слово «пишется», а слово «обозначается».
Источники:
- Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов
- Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра/ Под ред. П.Ф. Фильчакова
- Каплан И.А. Практические занятия по высшей математике
Дополнительная информация:
- ru.wikipedia.org – Список обозначений в физике
- azbyka.kz — Урок математики «Скорость, время, расстояние»
| Ускорение | |
 |
|
| Размерность |
LT−2 |
|---|---|
| Единицы измерения | |
| СИ |
м/с² |
| СГС |
см/с² |
Падающий мяч при отсутствии сопротивления воздуха ускоряется, то есть движется все быстрее и быстрее.
Ускоре́ние (обычно обозначается 

Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².
Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (m/s2, м/с2), существует также внесистемная единица Гал (Gal), применяемая в гравиметрии и равная 1 см/с2.
Производная ускорения по времени, то есть величина, характеризующая скорость изменения ускорения, называется рывок:
, где:
— вектор рывка.
Содержание
- 1 Кинематика точки
- 1.1 Ускорение точки при прямолинейном движении
- 1.2 Ускорение точки при движении по окружности
- 1.3 Ускорение точки при движении по кривой
- 2 Ускорения в твёрдом теле
- 3 Ускорение при сложном движении
- 4 Динамика точки
- 5 Единицы измерения ускорения
- 6 Измерение ускорения
- 7 Примеры ускорений
- 8 См. также
- 9 Примечания
- 10 Ссылки
Кинематика точки
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости материальной точки по времени:
.
Ускорение точки при прямолинейном движении
Если вектор 
.
Из вышеприведённых двух формул можно вывести ещё одну, связывающую скалярные величины:
Здесь 



Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное, вообще говоря, не верно).
Ускорение точки при движении по окружности
Вектор ускорения
при движении точки по окружности можно разложить на два слагаемых (компоненты):
Тангенциальное ускорение — 

Центростремительное или Нормальное ускорение 

Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.
Ускорение точки при движении по кривой
Вектор ускорения 

,
где


Векторы 

Итак, учитывая сказанное выше, вектор ускорения всегда можно записать как:
,
Ускорения в твёрдом теле
Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:
,
где 

Второе слагаемое называется осестремительным ускорением.
Ускорение при сложном движении
Говорят, что материальная точка (тело) совершает сложное движение, если она движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. Тогда абсолютное ускорение тела равно сумме относительного, переносного и кориолисова:
.
Динамика точки
Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчёта всегда является некоторое внешнее силовое воздействие.
Второй закон Ньютона утверждает, что ускорение материальной точки всегда пропорционально приложенной к ней и порождающей ускорение силе, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):
Единицы измерения ускорения
- метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ
- сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС
| м/с2 | фут/с2 | g0 | см/с2 | |
|---|---|---|---|---|
| 1 м/с2 = | 1 | 3.28084 | 0.101972 | 100 |
| 1 фут/с2 = | 0.304800 | 1 | 0.0310810 | 30.4800 |
| 1 g0 = | 9.80665 | 32.1740 | 1 | 980.665 |
| 1 см/с2 = | 0.01 | 0.0328084 | 0.00101972 | 1 |
Измерение ускорения
Приборы для измерения ускорения называются акселерометрами. Они не измеряют ускорение непосредственно, а измеряют силу реакции (укр.)русск. опоры, которая возникает при ускоренном движении. Поскольку аналогичные силы сопротивления возникают также и в поле тяготения, то с помощью акселерометров можно измерять также и гравитацию.
Акселерографы — приборы, измеряющие и автоматически записывающие (в виде графиков) значения ускорения поступательного и вращательного движения.
Примеры ускорений
Значения ускорений различных движений:[1]
| Вид движения | Ускорение, м/с2 |
|---|---|
| Аварийное торможение автомобиля | 4—6 |
| Автомобиль «Жигули» | 1,5 |
| Бегун на коротких дистанциях | 1,5 |
| Велосипедист | 1,7 |
| Гоночный автомобиль | 8—9 |
| Запуск и торможение космического корабля | 4—6 g |
| Конькобежец | 1,9 |
| Манёвр реактивного самолёта | до 10 g |
| Микрочастицы в ускорителе | (2—50) · 1014 |
| Мотоцикл | 3—6 |
| Пассажирский лифт | 0,9—1,6 |
| Поезд метро | 1 |
| Поршень двигателя внутреннего сгорания | 3 · 103 |
| Пуля в стволе винтовки | 2,5 · 105 |
| Свая после удара копром | 300 |
| Торможение при открытии парашюта | 3 g |
Примечание: g ≈ 9,81 м/с2.
См. также
| Ускорение в Викисловаре? | |
| Ускорение в Викитеке? | |
| Ускорение на Викискладе? |
- Ускорение свободного падения
- Релятивистски равноускоренное движение
Примечания
- ↑ Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. — 10-е, испр. и доп.. — М.: Наука, 1988. — С. 61. — 256 с. — ISBN 5-02-013833-9
Ссылки
- Ландау, Л. Д., Лифшиц, Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6












![{displaystyle {begin{aligned}mathbf {s} (t)&=mathbf {s} _{0}+mathbf {v} _{0}t+{tfrac {1}{2}}mathbf {a} t^{2}=mathbf {s} _{0}+{tfrac {1}{2}}left(mathbf {v} _{0}+mathbf {v} (t)right)t\mathbf {v} (t)&=mathbf {v} _{0}+mathbf {a} t\{v^{2}}(t)&={v_{0}}^{2}+2mathbf {acdot } [mathbf {s} (t)-mathbf {s} _{0}]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a604fcb59c070efb1687e12fe2a99799d2fb3a9b)







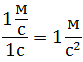

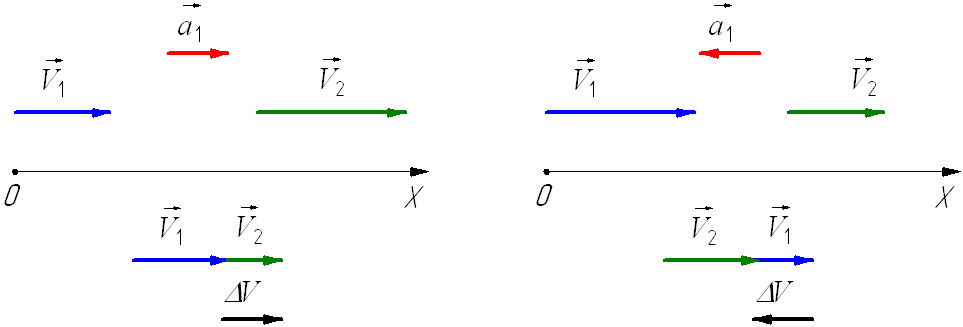
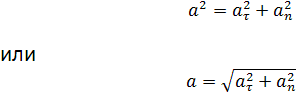

 , где:
, где:  — вектор рывка.
— вектор рывка. .
.
 .
.






 ,
, ,
,![vec{w}_B = vec{w}_A + left[vec{omega}, left[ vec{omega}, vec{AB}right] right] + left[ varepsilon, vec{AB} right]](https://dic.academic.ru/dic.nsf/ruwiki/3e27aa54ea841bf57cd0aa5554e07bf5.png) ,
,![vec a_a=vec {a}_r + vec {a}_e + 2left[vec omega times vec {v}_r right]](https://dic.academic.ru/dic.nsf/ruwiki/2bb4936c467fcb4f36cd35d23434328c.png) .
.