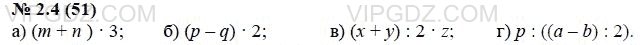Col Baskakov
СЕМЬ ПЛЮС ПЯТЬ КАК ПИШИТСЯ ОДИНАТЦАТЬ ИЛИ ДВЕНАДЦАТЬ
Ответы

Елена Crimea
ПишЕтся одинНаДцать. А семь плюс пять — двенадцать. Здесь правильно.

Юлия Тарасова (Раковская)
11-пишется одиннадцать а в примере получится двенадцать
5 лет

Maria Cheltuitor
ТРИНАДЦАТЬ Нажмите,
чтобы загрузить
GIF
Col Baskakov
Maria Cheltuitor
Нажмите,
чтобы загрузить
GIF ВЫШАЯ МАТЕМАТИКА

Марина
Пеши тринацать — на всякий случай!

Людмила Козырь
Col Baskakov
УРА 5 ПОЛУЧИЛАБЫ НЕБЫЛАБ ТАК МОЛОДА
Людмила Козырь
были и мы когда то молодыми
Col Baskakov

Валерия Гальянова
Пишется- двенадцать
5 лет
Col Baskakov
ЛВ
Любовь Веселова
и куда Вас такое желание заведет? Ведь аппетит приходит во время еды….
Col Baskakov

Михаил Куринный

Елена

Маркиза Простая Баба

Лена Шашкова
Col Baskakov
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
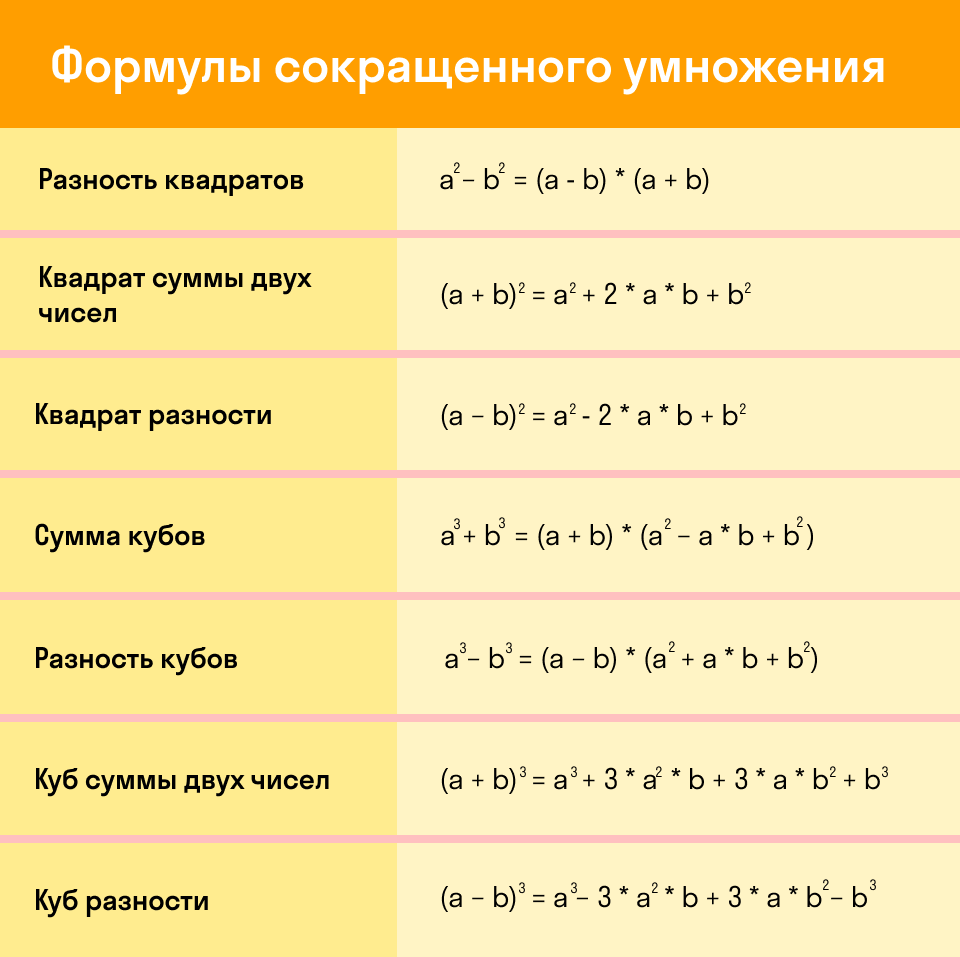
Формулы сокращенного умножения
Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.
Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.
Как читать формулы сокращенного умножения
Учимся проговаривать формулы сокращенного выражения:
- Разность квадратов двух выражений равна произведению их разности и их суммы.
- Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.
- Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.
- Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
- Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
- Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
- Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.
Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.
Доказательство формул сокращенного умножения
Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a2 — b2 = (a — b) * (a + b).
Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a2 — b2.
Важно знать, что разность квадратов не равна квадрату разности: a2 — b2 ≠ (a — b)2.
Докажем, что a2 — b2 = (a — b) * (a + b).
Поехали:
- Используя искусственный метод, прибавим и отнимем одно и тоже a * b.
+ a * b — a * b = 0
a2 — b2 = a2 — b2 + ab — ab
- Сгруппируем иначе: a2 — b2 + a * b — a * b = a2 — a * b + a * b — b2
- Продолжим группировать: a2 — a * b — b2 +a * b = (a2 — a * b) + (a * b — b2)
- Вынесем общие множители за скобки:
(a2 — a * b) + (a * b — b2) = a *(a — b) + b *(a — b)
- Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)
- Результат доказательства: a2 — b2 = (a — b) * (a + b)
- Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a2 — b2, нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a2 — b2.
Остальные ФСУ можно доказать аналогичным методом.
Дополнительные формулы сокращенного умножения
К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.
Бином Ньютона
Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:
Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:
ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
(a1+a2+…+an)2 = a12 + a22 + … + an-12 + an2 + 2 * a1 * a2 + 2 * a1 * a3 + 2 * a1 * a4 + … +
+ 2 * a1 * an-1 + 2 * a1 * an + 2 * a2 * a3 + 2 * a2 * a4 + … + 2 * a2 * an-1 + 2 * a2 * an +…+
+ 2 * an-1 * an
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
an − bn = (a − b) * (an-1 + an-2 * b + an-3 * b2 + … + a * bn-2 + bn-1).
Для четных показателей можно записать так:
a2*m − b2*m = (a2 − b2) *(a2*m−2 + a2*m−4 * b2 + a2*m−6 * b4 + … + b2*m−2).
Для нечетных показателей:
a2*m+1 − b2*·m+1 = (a − b) * (a2*m + a2*m−1 * b + a2*m−2 * b2 + … + b2*m).
Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.
Решение задач
Давайте потренируемся и рассмотрим примеры с дробями.
Задание 1
Что сделать: вычислить квадрат произведения (55 + 10)2.
Как решаем: воспользуемся формулой квадрата суммы: (55 + 10)2 = 552 + 2 * 55 * 10 + 102 = 3025 + 1100 + 100 = 4225.
Задание 2
Что сделать: упростить выражение 64 * с3 – 8.
Как решаем: применим разность кубов: 64 * с3 – 8 = (4 * с)3 – 23 = (4 * с – 2)((4 * с)2 + 4 * с * 2 + 22) = (4 * с – 2)(16 * с2 + 8 * с + 4).
Задание 3
Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).
Как решаем:
- Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y2 + 7 * y * x — 7 * y * x — x2 = 49 * y2 — x2.
- Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y)2 — x2 = 49 * y2 — x2.
Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей
0 интересует
0 не интересует
15 просмотров
Запишите выражение: а)произведение m и n;б)утроенная сумма a и b;в)сумма произведений чисел 6 и x и чисел 8 и y;г)произведение разности чисел а и b и числа с. очень надо срочно помогите зарание спс
- чисел
- произведение
- сумма
- запишите
- выражение
- утроенная
- 5 — 9 классы
- математика
спросил
15 Март, 18
от
Аришоочек_zn
(42 баллов)
в категории Математика
1 Ответ
0 интересует
0 не интересует
ответил
15 Март, 18
от
Raha007_zn
(14 баллов)
1. m*n 2.(a+b) * 3 3. (6*x)+(8*y) 4.(a-b) * c
Добро пожаловать на сайт Правильные Ответы и Решения.
16 видели
Запишите выражение:
a)произведение m и n;
б)утроенная сумма a и b;
в)сумма произведений чисел 6 и x и чисел 8 и y;
г)произведение разности чисел а и b и числа c.
Помогите ребята!!!
- чисел
- произведение
- сумма
- запишите
- выражение
- утроенная
- 5 — 9 классы
- математика
Задание
09 Май, 18
от
SINON111_zn
(44 баллов)
в разделе Математика
|
16 видели
Помощь с домашними заданиями. Решение задач, ответы на вопросы учеников и студентов.
OTVETYTUT.COM — 2018
Главная
Контакты
Содержание
- Что значит утроенная сумма чисел в математике?
- Утроенная сумма чисел m и n
- Условие
- Решение 1
- Решение 2
- Популярные решебники
- Другие вопросы из категории
- Читайте также
- Что такое утроенная разность чисел? Примеры?
Что значит утроенная сумма чисел в математике?
Что такое утроенная сумма чисел, примеры?
Как записать утроенную сумму чисел а и b?
Это значит сложить числа a и b и получившийся результат умножить на 3.
берем сумму чисел a и b, умножаем потом это на 3. (a+b)*3 Можно записать по-другому, как a*3+b*3
Пример. a=1 b=0,001
А вы скажите, с чего такие вопросы? Это же не формулы какие-то, а просто сумма и умножение чисел. Ничего она не значит, обычные арифметические действия.
Нет одной «волшебной» формулы. Есть примеры, предназначенные специально для того, чтоб их долго решали, так как они направлены на развитие счета в уме. Но есть и примеры, предназначенные для решения по формулам.
В школе Вас могли учить «формулам сокращенного умножения», выносу за скобки и группировке.
Формул много, каждая для отдельного случая.
-вынос за скобки
ab+ac = a(b+c)
25 * 254 — 25 * 250 = 25 * (254 — 250) = 25 * 4 = 100
Вспомните основное правило раскрытия скобок — если перед скобкой стоит знак «минус», то стоящий за скобкой знак меняется на противоположный.
Если стоит «плюс», то знак за скобкой остается без изменения.
В Вашем примере перед скобкой стоит «плюс», следовательно, суммируем следующие числа -3 и -45 и получаем в ответе -48 (минус сорок восемь).
Если в четыре раза меньше, то это 41х и 82х, у каждого этого набора по 10 вариантов единиц, следовательно, таких чисел 20 штук:
410, 411, 412. 419,
820, 821, 822. 829.
Это двоичный код. Если у двоичного числа все нули заменить на единицы, а все единицы — на нули, то получится обратный код. При сложении с исходным числом, он дает все единицы в сумме. А если к обратномку коду прибавить один, то получится дополнительный код, который при сложении дает все нули. Это используется для подсчета контрольных сумм.
Казалось бы, в извлечении корня нет никакой сложности — используется метод последовательных приближений, например, метод половинного деления для решения уравнения x^2=a, придуманный для извлечения корня еще в Вавилоне. Однако 12-разрядное число — это 40 двоичных бит, то есть уравнение с заданной точностью решается за 40 итераций, на каждой из которых необходимо возводить в квадрат, то есть совершать весьма медленную операцию умножения. При отсутствии быстродействующего аппаратного умножителя (наличие которого трудно ожидать в калькуляторе) каждое умножение (в той же 12-разрядной сетке, которая 40 бит) выливается в
40 сложений и 40 сдвигов, к которым добавляются проверки условий и условные переходы. В результате только одних математических операций (сложений и сдвигов) за одно извлечение корня придется выполнить 3200 штук, плюс еще столько же вспомогательных.
Это сегодня процессор, выполняющий 50 миллионов операций в секунду и выполняющий 32-разрядное умножение (как и сложение) за один такт, стоит меньше доллара. Но раньше было не так, и чтобы калькулятор помещался на столе и стоил не как спортивный автомобиль или даже квартира в центре Нью-Йорка, разработчики были вынуждены сильно упрощать вычислительные блоки. Никаких параллельных АЛУ, все операции — последовательные, бит за битом. Операция сложения 12-разрядных чисел разворачивается в 48 операций двоичного сложения (48 — потому что использовалась двоично-десятичная кодировка, опять же, ради упрощения схемы), каждая — в лучшем случае за один такт. Тактовая частота — килогерцы, сложение за десятки миллисекунд, умножение — за полсекунды. Извлечение корня по такому алгоритму заняло бы десятки секунд.
Метод Ньютона, взятый «в лоб», ускоряет сходимость, да требует деления. А оно страшно долгое и выигрыша не получается.
Поэтому в калькуляторах применили алгоритмы, которые еще в доэлектронную эру использовали для извлечения корня на бумаге, а позже на арифмометре. Только с учетом того, что деление — операция долгая, как я говорил, а вот сдвиг — то же деление, только на 2,4 и т.д.
Источник
Утроенная сумма чисел m и n
Запишите на математическом языке:
а) Утроенную сумму чисел m и n;
б) удвоенную разность чисел p и q;
в) произведение полусуммы чисел х и у и числа z;
г) частное от деления числа р на полуразность чисел a и b.
Условие
Решение 1
Решение 2
Поиск в решебнике
Популярные решебники
Издатель: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, 2013г.
Издатель: А.Г. Мордкович, 2013г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2015г.
3(m+n)
утроенную сумму чисел m и n; 3 * (m + n)
Другие вопросы из категории
яблок меньше, чем в коробку?
С помощью графика найдите:
1)область определения функции
2)область значения функции
3)промежутки, в которых y>0,y 5-9 класс алгебра ответов 1
Читайте также
клеточках, расположенных по вертикали, должна равняться сумме чисел в трех клеточках, расположенных по горизонтали. Укажите самое большое значение этой суммы.
в)сумму числа 4 и суммы чисел 8,3 и 2,7
г)разность суммы числа 17 и разности чисел 7 и 5
д)разность суммы чисел 1,6 и 1,7 и числа 2
е)сумму разности чисел 1,6 и 1,7 и числа 2,2
Ж0разность разности чисел 20,5 и 10,7 и числа 5,7
произвидение суммы чисел m и k и квадрата числа n:
в)часное от деления суммы куба числа a и удвоенного чимла b на произведение чисел p и q :
Источник
Что такое утроенная разность чисел? Примеры?
Как записать утроенную разность чисел a и b?
Я думаю это как раз разность этих чисел, умноженная на 3. Здесь не оговаривается эта разность должна быть положительным числом или любым. Потому что от того из какого числа вычесть другое будет зависеть знак результата. Можно посчитать по модулю. Модуль 3*(a-b).
-8*3=-24. Модуль этого числа 24.
На мой взгляд это будет как-то так:(a-b)*3,где (a-b)- это разность чисел «a» и «b».Цифра «3»- это множитель. Тогда и получается утроенная разность чисел a и b. Здесь главное не перепутать с возведением в третью степень ((a-b)^3) и с разностью утроенных чисел «a» и «b» (3a- 3b).Как-то так, на мой взгляд получается.
Наверно так. Давно правда это было,но хочется вспомнить a—b=3x или 8—5=3×3, если объясняете ребенку,обязательно вспомните с ним,что такое разность ,утроенное,значит умноженное на три.
В пятом классе в учебнике по математике попадались такие задачи.
Нужно записать в буквенном выражении утроенную разность чисел a и b.
Утроенная, значит умноженная на три.
Для этого А и В нужно выделить скобками и умножить на 3.
Пишем (a-b)*3 или 3(a-b)
Нет одной «волшебной» формулы. Есть примеры, предназначенные специально для того, чтоб их долго решали, так как они направлены на развитие счета в уме. Но есть и примеры, предназначенные для решения по формулам.
В школе Вас могли учить «формулам сокращенного умножения», выносу за скобки и группировке.
Формул много, каждая для отдельного случая.
-вынос за скобки
ab+ac = a(b+c)
25 * 254 — 25 * 250 = 25 * (254 — 250) = 25 * 4 = 100
Вспомните основное правило раскрытия скобок — если перед скобкой стоит знак «минус», то стоящий за скобкой знак меняется на противоположный.
Если стоит «плюс», то знак за скобкой остается без изменения.
В Вашем примере перед скобкой стоит «плюс», следовательно, суммируем следующие числа -3 и -45 и получаем в ответе -48 (минус сорок восемь).
Если в четыре раза меньше, то это 41х и 82х, у каждого этого набора по 10 вариантов единиц, следовательно, таких чисел 20 штук:
410, 411, 412. 419,
820, 821, 822. 829.
Это двоичный код. Если у двоичного числа все нули заменить на единицы, а все единицы — на нули, то получится обратный код. При сложении с исходным числом, он дает все единицы в сумме. А если к обратномку коду прибавить один, то получится дополнительный код, который при сложении дает все нули. Это используется для подсчета контрольных сумм.
Казалось бы, в извлечении корня нет никакой сложности — используется метод последовательных приближений, например, метод половинного деления для решения уравнения x^2=a, придуманный для извлечения корня еще в Вавилоне. Однако 12-разрядное число — это 40 двоичных бит, то есть уравнение с заданной точностью решается за 40 итераций, на каждой из которых необходимо возводить в квадрат, то есть совершать весьма медленную операцию умножения. При отсутствии быстродействующего аппаратного умножителя (наличие которого трудно ожидать в калькуляторе) каждое умножение (в той же 12-разрядной сетке, которая 40 бит) выливается в
40 сложений и 40 сдвигов, к которым добавляются проверки условий и условные переходы. В результате только одних математических операций (сложений и сдвигов) за одно извлечение корня придется выполнить 3200 штук, плюс еще столько же вспомогательных.
Это сегодня процессор, выполняющий 50 миллионов операций в секунду и выполняющий 32-разрядное умножение (как и сложение) за один такт, стоит меньше доллара. Но раньше было не так, и чтобы калькулятор помещался на столе и стоил не как спортивный автомобиль или даже квартира в центре Нью-Йорка, разработчики были вынуждены сильно упрощать вычислительные блоки. Никаких параллельных АЛУ, все операции — последовательные, бит за битом. Операция сложения 12-разрядных чисел разворачивается в 48 операций двоичного сложения (48 — потому что использовалась двоично-десятичная кодировка, опять же, ради упрощения схемы), каждая — в лучшем случае за один такт. Тактовая частота — килогерцы, сложение за десятки миллисекунд, умножение — за полсекунды. Извлечение корня по такому алгоритму заняло бы десятки секунд.
Метод Ньютона, взятый «в лоб», ускоряет сходимость, да требует деления. А оно страшно долгое и выигрыша не получается.
Поэтому в калькуляторах применили алгоритмы, которые еще в доэлектронную эру использовали для извлечения корня на бумаге, а позже на арифмометре. Только с учетом того, что деление — операция долгая, как я говорил, а вот сдвиг — то же деление, только на 2,4 и т.д.
Источник
-
Знаешь ответ? Добавь его сюда!
-
Русский язык6 минут назад
Помогите, пожалуйста,с русским!
Задание ниже на фото,заранее огромное спасибо. -
Геометрия15 минут назад
ПОМОГИТЕ БЫСТРЕЕ! ДО УРОКА ЧУТЬ ЧУТЬ! ПЛИЗЗЗЗЗЗ!!!!!!!!!! (7 класс)
-
Литература26 минут назад
Характеристика героя пожалуйста
-
История31 минут назад
Краткий перессказ по истор «США до середины 19в. , рабовладение, демократия, экономический рост.»
-
Українська мова31 минут назад
Випишіть безсполучникові складні речення.
Підкресліть граматичні основи, накресліть схеми
Шануй і поважай матір і батька: вони дали тобі життя
Своєю працею й піклуванням вони несуть радість у твою колиску.
Не забувай, що батьки також мають право на радість.
Батьки ночей не спали біля твоєї колиски, вони прислухались до твого дихання, до биття твого серця.
Дорожи честю сім’ї, оберігай її, як святиню.
Де б ти не був, ніколи не забувай про свою рідну домівку
Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.