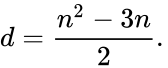The diagonals of a cube with side length 1. AC’ (shown in blue) is a space diagonal with length 

In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word diagonal derives from the ancient Greek διαγώνιος diagonios,[1] «from angle to angle» (from διά- dia-, «through», «across» and γωνία gonia, «angle», related to gony «knee»); it was used by both Strabo[2] and Euclid[3] to refer to a line connecting two vertices of a rhombus or cuboid,[4] and later adopted into Latin as diagonus («slanting line»).
In matrix algebra, the diagonal of a square matrix consists of the entries on the line from the top left corner to the bottom right corner.
There are also other, non-mathematical uses.
Non-mathematical uses[edit]
A stand of basic scaffolding on a house construction site, with diagonal braces to maintain its structure
In engineering, a diagonal brace is a beam used to brace a rectangular structure (such as scaffolding) to withstand strong forces pushing into it; although called a diagonal, due to practical considerations diagonal braces are often not connected to the corners of the rectangle.
Diagonal pliers are wire-cutting pliers defined by the cutting edges of the jaws intersects the joint rivet at an angle or «on a diagonal», hence the name.
A diagonal lashing is a type of lashing used to bind spars or poles together applied so that the lashings cross over the poles at an angle.
In association football, the diagonal system of control is the method referees and assistant referees use to position themselves in one of the four quadrants of the pitch.
Polygons[edit]
As applied to a polygon, a diagonal is a line segment joining any two non-consecutive vertices. Therefore, a quadrilateral has two diagonals, joining opposite pairs of vertices. For any convex polygon, all the diagonals are inside the polygon, but for re-entrant polygons, some diagonals are outside of the polygon.
Any n-sided polygon (n ≥ 3), convex or concave, has 
|
|
|
|
|
Regions formed by diagonals[edit]
In a convex polygon, if no three diagonals are concurrent at a single point in the interior, the number of regions that the diagonals divide the interior into is given by
For n-gons with n=3, 4, … the number of regions is[5]
- 1, 4, 11, 25, 50, 91, 154, 246…
This is OEIS sequence A006522.[6]
Intersections of diagonals[edit]
If no three diagonals of a convex polygon are concurrent at a point in the interior, the number of interior intersections of diagonals is given by 
Regular polygons[edit]
There exist separate formulae for calculating the length of the longest diagonal in regular polygons with an even or odd number of sides.
In an even-sided regular polygon with n sides and side length a, the length of the longest diagonal is equivalent to the diameter of its circumcircle because the long diagonals all intersect each other at the polygon’s center. This is given by the following formula.
The length of the longest diagonal of any odd-sided regular n-sided polygon (n ≥ 5) with side length a is given by the following formula.[9]
The length of a polygon’s shortest diagonal can also be calculated for all polygons (n ≥ 4) with the following formula.[10] As the number of sides approaches infinity, the shortest diagonal approaches 2a.
These are not applicable for a triangle which has no diagonals.
Special cases include:
A square has two diagonals of equal length, which intersect at the center of the square. The ratio of a diagonal to a side is 
A regular pentagon has five diagonals all of the same length. The ratio of a diagonal to a side is the golden ratio, 
A regular hexagon has nine diagonals: the six shorter ones are equal to each other in length; the three longer ones are equal to each other in length and intersect each other at the center of the hexagon. The ratio of a long diagonal to a side is 2, and the ratio of a short diagonal to a side is 
A regular heptagon has 14 diagonals. The seven shorter ones equal each other, and the seven longer ones equal each other. The reciprocal of the side equals the sum of the reciprocals of a short and a long diagonal.
In general a regular n-gon has 
Polyhedrons[edit]
A polyhedron (a solid object in three-dimensional space, bounded by two-dimensional faces) may have two different types of diagonals: face diagonals on the various faces, connecting non-adjacent vertices on the same face; and space diagonals, entirely in the interior of the polyhedron (except for the endpoints on the vertices).
Just as a triangle has no diagonals, so also a tetrahedron (with four triangular faces) has no face diagonals and no space diagonals.
A cuboid has two diagonals on each of the six faces and four space diagonals.
Matrices[edit]
For a square matrix, the diagonal (or main diagonal or principal diagonal) is the diagonal line of entries running from the top-left corner to the bottom-right corner.[11][12][13] For a matrix 




The top-right to bottom-left diagonal is sometimes described as the minor diagonal or antidiagonal.
The off-diagonal entries are those not on the main diagonal. A diagonal matrix is one whose off-diagonal entries are all zero.[14][15]
A superdiagonal entry is one that is directly above and to the right of the main diagonal.[16][17] Just as diagonal entries are those 


Likewise, a subdiagonal entry is one that is directly below and to the left of the main diagonal, that is, an entry 








Geometry[edit]
By analogy, the subset of the Cartesian product X×X of any set X with itself, consisting of all pairs (x,x), is called the diagonal, and is the graph of the equality relation on X or equivalently the graph of the identity function from X to X. This plays an important part in geometry; for example, the fixed points of a mapping F from X to itself may be obtained by intersecting the graph of F with the diagonal.
In geometric studies, the idea of intersecting the diagonal with itself is common, not directly, but by perturbing it within an equivalence class. This is related at a deep level with the Euler characteristic and the zeros of vector fields. For example, the circle S1 has Betti numbers 1, 1, 0, 0, 0, and therefore Euler characteristic 0. A geometric way of expressing this is to look at the diagonal on the two-torus S1xS1 and observe that it can move off itself by the small motion (θ, θ) to (θ, θ + ε). In general, the intersection number of the graph of a function with the diagonal may be computed using homology via the Lefschetz fixed-point theorem; the self-intersection of the diagonal is the special case of the identity function.
See also[edit]
- Jordan normal form
- Main diagonal
- Diagonal functor
Notes[edit]
- ^ Online Etymology Dictionary
- ^ Strabo, Geography 2.1.36–37
- ^ Euclid, Elements book 11, proposition 28
- ^ Euclid, Elements book 11, proposition 38
- ^ Weisstein, Eric W. «Polygon Diagonal.» From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/PolygonDiagonal.html
- ^ Sloane, N. J. A. (ed.). «Sequence A006522». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Poonen, Bjorn; Rubinstein, Michael. «The number of intersection points made by the diagonals of a regular polygon». SIAM J. Discrete Math. 11 (1998), no. 1, 135–156; link to a version on Poonen’s website
- ^ [1], beginning at 2:10
- ^ «Murderous Maths: The LOngest Diagonal Formula!».
- ^ «Length of Diagonal of a n-sided regular polygon». 2 January 2019.
- ^ Bronson (1970, p. 2)
- ^ Herstein (1964, p. 239)
- ^ Nering (1970, p. 38)
- ^ Herstein (1964, p. 239)
- ^ Nering (1970, p. 38)
- ^ Bronson (1970, pp. 203, 205)
- ^ Herstein (1964, p. 239)
- ^ Cullen (1966, p. 114)
References[edit]
- Bronson, Richard (1970), Matrix Methods: An Introduction, New York: Academic Press, LCCN 70097490
- Cullen, Charles G. (1966), Matrices and Linear Transformations, Reading: Addison-Wesley, LCCN 66021267
- Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley, LCCN 76091646
External links[edit]
Look up diagonal in Wiktionary, the free dictionary.
- Diagonals of a polygon with interactive animation
- Polygon diagonal from MathWorld.
- Diagonal of a matrix from MathWorld.
The diagonals of a cube with side length 1. AC’ (shown in blue) is a space diagonal with length 

In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word diagonal derives from the ancient Greek διαγώνιος diagonios,[1] «from angle to angle» (from διά- dia-, «through», «across» and γωνία gonia, «angle», related to gony «knee»); it was used by both Strabo[2] and Euclid[3] to refer to a line connecting two vertices of a rhombus or cuboid,[4] and later adopted into Latin as diagonus («slanting line»).
In matrix algebra, the diagonal of a square matrix consists of the entries on the line from the top left corner to the bottom right corner.
There are also other, non-mathematical uses.
Non-mathematical uses[edit]
A stand of basic scaffolding on a house construction site, with diagonal braces to maintain its structure
In engineering, a diagonal brace is a beam used to brace a rectangular structure (such as scaffolding) to withstand strong forces pushing into it; although called a diagonal, due to practical considerations diagonal braces are often not connected to the corners of the rectangle.
Diagonal pliers are wire-cutting pliers defined by the cutting edges of the jaws intersects the joint rivet at an angle or «on a diagonal», hence the name.
A diagonal lashing is a type of lashing used to bind spars or poles together applied so that the lashings cross over the poles at an angle.
In association football, the diagonal system of control is the method referees and assistant referees use to position themselves in one of the four quadrants of the pitch.
Polygons[edit]
As applied to a polygon, a diagonal is a line segment joining any two non-consecutive vertices. Therefore, a quadrilateral has two diagonals, joining opposite pairs of vertices. For any convex polygon, all the diagonals are inside the polygon, but for re-entrant polygons, some diagonals are outside of the polygon.
Any n-sided polygon (n ≥ 3), convex or concave, has 
|
|
|
|
|
Regions formed by diagonals[edit]
In a convex polygon, if no three diagonals are concurrent at a single point in the interior, the number of regions that the diagonals divide the interior into is given by
For n-gons with n=3, 4, … the number of regions is[5]
- 1, 4, 11, 25, 50, 91, 154, 246…
This is OEIS sequence A006522.[6]
Intersections of diagonals[edit]
If no three diagonals of a convex polygon are concurrent at a point in the interior, the number of interior intersections of diagonals is given by 
Regular polygons[edit]
There exist separate formulae for calculating the length of the longest diagonal in regular polygons with an even or odd number of sides.
In an even-sided regular polygon with n sides and side length a, the length of the longest diagonal is equivalent to the diameter of its circumcircle because the long diagonals all intersect each other at the polygon’s center. This is given by the following formula.
The length of the longest diagonal of any odd-sided regular n-sided polygon (n ≥ 5) with side length a is given by the following formula.[9]
The length of a polygon’s shortest diagonal can also be calculated for all polygons (n ≥ 4) with the following formula.[10] As the number of sides approaches infinity, the shortest diagonal approaches 2a.
These are not applicable for a triangle which has no diagonals.
Special cases include:
A square has two diagonals of equal length, which intersect at the center of the square. The ratio of a diagonal to a side is 
A regular pentagon has five diagonals all of the same length. The ratio of a diagonal to a side is the golden ratio, 
A regular hexagon has nine diagonals: the six shorter ones are equal to each other in length; the three longer ones are equal to each other in length and intersect each other at the center of the hexagon. The ratio of a long diagonal to a side is 2, and the ratio of a short diagonal to a side is 
A regular heptagon has 14 diagonals. The seven shorter ones equal each other, and the seven longer ones equal each other. The reciprocal of the side equals the sum of the reciprocals of a short and a long diagonal.
In general a regular n-gon has 
Polyhedrons[edit]
A polyhedron (a solid object in three-dimensional space, bounded by two-dimensional faces) may have two different types of diagonals: face diagonals on the various faces, connecting non-adjacent vertices on the same face; and space diagonals, entirely in the interior of the polyhedron (except for the endpoints on the vertices).
Just as a triangle has no diagonals, so also a tetrahedron (with four triangular faces) has no face diagonals and no space diagonals.
A cuboid has two diagonals on each of the six faces and four space diagonals.
Matrices[edit]
For a square matrix, the diagonal (or main diagonal or principal diagonal) is the diagonal line of entries running from the top-left corner to the bottom-right corner.[11][12][13] For a matrix 




The top-right to bottom-left diagonal is sometimes described as the minor diagonal or antidiagonal.
The off-diagonal entries are those not on the main diagonal. A diagonal matrix is one whose off-diagonal entries are all zero.[14][15]
A superdiagonal entry is one that is directly above and to the right of the main diagonal.[16][17] Just as diagonal entries are those 


Likewise, a subdiagonal entry is one that is directly below and to the left of the main diagonal, that is, an entry 








Geometry[edit]
By analogy, the subset of the Cartesian product X×X of any set X with itself, consisting of all pairs (x,x), is called the diagonal, and is the graph of the equality relation on X or equivalently the graph of the identity function from X to X. This plays an important part in geometry; for example, the fixed points of a mapping F from X to itself may be obtained by intersecting the graph of F with the diagonal.
In geometric studies, the idea of intersecting the diagonal with itself is common, not directly, but by perturbing it within an equivalence class. This is related at a deep level with the Euler characteristic and the zeros of vector fields. For example, the circle S1 has Betti numbers 1, 1, 0, 0, 0, and therefore Euler characteristic 0. A geometric way of expressing this is to look at the diagonal on the two-torus S1xS1 and observe that it can move off itself by the small motion (θ, θ) to (θ, θ + ε). In general, the intersection number of the graph of a function with the diagonal may be computed using homology via the Lefschetz fixed-point theorem; the self-intersection of the diagonal is the special case of the identity function.
See also[edit]
- Jordan normal form
- Main diagonal
- Diagonal functor
Notes[edit]
- ^ Online Etymology Dictionary
- ^ Strabo, Geography 2.1.36–37
- ^ Euclid, Elements book 11, proposition 28
- ^ Euclid, Elements book 11, proposition 38
- ^ Weisstein, Eric W. «Polygon Diagonal.» From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/PolygonDiagonal.html
- ^ Sloane, N. J. A. (ed.). «Sequence A006522». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Poonen, Bjorn; Rubinstein, Michael. «The number of intersection points made by the diagonals of a regular polygon». SIAM J. Discrete Math. 11 (1998), no. 1, 135–156; link to a version on Poonen’s website
- ^ [1], beginning at 2:10
- ^ «Murderous Maths: The LOngest Diagonal Formula!».
- ^ «Length of Diagonal of a n-sided regular polygon». 2 January 2019.
- ^ Bronson (1970, p. 2)
- ^ Herstein (1964, p. 239)
- ^ Nering (1970, p. 38)
- ^ Herstein (1964, p. 239)
- ^ Nering (1970, p. 38)
- ^ Bronson (1970, pp. 203, 205)
- ^ Herstein (1964, p. 239)
- ^ Cullen (1966, p. 114)
References[edit]
- Bronson, Richard (1970), Matrix Methods: An Introduction, New York: Academic Press, LCCN 70097490
- Cullen, Charles G. (1966), Matrices and Linear Transformations, Reading: Addison-Wesley, LCCN 66021267
- Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley, LCCN 76091646
External links[edit]
Look up diagonal in Wiktionary, the free dictionary.
- Diagonals of a polygon with interactive animation
- Polygon diagonal from MathWorld.
- Diagonal of a matrix from MathWorld.
Диагональ (греч. διαγώνιος от δια- «через» и γώνια «угол») в математике имеет геометрический смысл, а также используется при описании квадратных матриц.
Шестиугольник с диагоналями
Многоугольники и многогранники
Для многоугольников, диагональ это отрезок, соединяющий две вершины, не лежащие на одной стороне. Так, четырёхугольник имеет две диагонали, соединяющие противолежащие вершины. У выпуклого многоугольника диагонали проходят внутри него. Многоугольник выпуклый тогда и только тогда, когда его диагонали лежат внутри.
Пусть 


,
однако, мы посчитали каждую диагональ дважды (по разу для каждого конца) — отсюда,
Диагональю многогранника называется отрезок, соединяющий две его вершины, не принадлежащие одной грани. Так, на изображении куба отмечена диагональ 

Аналогично можно определить диагональ и для многогранников в пространствах бо́льших размерностей.
Матрицы
В случае с квадратными матрицами, главная диагональ является диагональной линией элементов, которая проходит с северо-запада на юго-восток. Например, единичная матрица может быть описана, как матрица, имеющая единицы на главной диагонали и нули вне её. Диагональ с юго-запада на северо-восток часто называется побочной диагональю. Наддиагональными элементами называются такие, что лежат выше и правее главной диагонали. Поддиагональными — те, что ниже и левее. Диагональная матрица — такая матрица, у которой все элементы вне главной диагонали равны нулю.
Теория множеств
По аналогии, подмножество декартового произведения X×X произвольного множества X на само себя, состоящее из пар элементов (x, x), называется диагональю множества. Это — единичное отношение, оно играет важную роль в геометрии: например, константные элементы отображения F с X в X могут быть получены сечением F с диагональю множества X.
Внешние ссылки
- Диагонали многоугольника с интерактивными анимациями
- Диагонали многоугольника с MathWorld.
- Диагонали матриц от MathWorld.
ДИАГОНАЛЬ
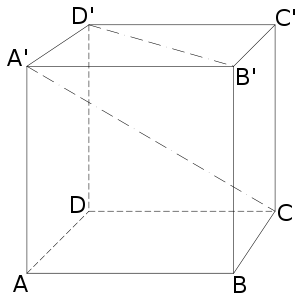
-отрезок прямой, соединяющий две вершины многоугольника (многогранника), не лежащие на одной стороне (на одной грани). Если число вершин многоугольника равно п, то число его Д. равно п( п-3)/2.
Е. В. Шикин.
Синонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬНАЯ ГРУППА →← ДИАГОНАЛИЗИРУЕМАЯ АЛГЕБРАИЧЕСКАЯ ГРУППА
Синонимы слова «ДИАГОНАЛЬ»:
ДОЛОНЬ, ИСКОСИНА, КОСЕК, ЛИНИЯ, СПЕЦДИАГОНАЛЬ, ТКАНЬ
Смотреть что такое ДИАГОНАЛЬ в других словарях:
ДИАГОНАЛЬ
ДИАГОНАЛЬ, -и, ж. 1. В математике: отрезок прямой линии, соединяющийдве вершины многоугольника, не лежащие на одной стороне, или две вершинымногогранника, не лежащие на одной грани. 2. Ткань с косыми рубчиками. * Подиагонали — наискось, не под прямым углом. Разлиновать лист по диагонали. прил. диагональный, -ая, -ое (к 1 знач.) и диагоналевый, -ая, -ое (ко 2знач.)…. смотреть
ДИАГОНАЛЬ
диагональ 1. ж. Отрезок прямой линии, соединяющий две несмежные вершины многоугольника, не лежащие на одной стороне или две вершины многогранника, не принадлежащие одной грани (в математике). 2. ж. Хлопчатобумажная или шерстяная ткань с отчетливо выраженными наклонными рубчиками.<br><br><br>… смотреть
ДИАГОНАЛЬ
диагональ ж.1. (линия) diagonal расположить по диагонали (вн.) — place diagonally (d.) 2. текст. diagonal
ДИАГОНАЛЬ
диагональ
сущ., кол-во синонимов: 6
• долонь (6)
• искосина (4)
• косек (5)
• линия (182)
• спецдиагональ (1)
• ткань (474)
Словарь синонимов ASIS.В.Н. Тришин.2013.
.
Синонимы:
долонь, искосина, линия, спецдиагональ, ткань… смотреть
ДИАГОНАЛЬ
ДИАГОНАЛЬ, плотная ткань из хл.-бум.
или шерстяной кручёной пряжи. Для Д. характерны резко выраженные рубчики
на поверхности, расположенные под углом… смотреть
ДИАГОНАЛЬ
ДИАГОНАЛЬ (лат. diagonalis, от греч.
diagonios — идущий от угла к углу), 1) Д. многоугольника — отрезок прямой,
соединяющий две его вершины, не лежащ… смотреть
ДИАГОНАЛЬ
Диагональ — см. Переплетение нитей в тканях.
ДИАГОНАЛЬ
ДИАГОНАЛЬ(греч., от dia — чрез, и gonia — угол). 1) прямая линия, соединяющая в прямолинейной фигуре вершины двух углов, не лежащие на одной прямой. 2)… смотреть
ДИАГОНАЛЬ
I.
ДИАГОНАЛЬ I и, ж. diagonale f. <, лат. diagonalis <гр. diagonis идущий от угла к углу. мат. Некоего четвероуголия не равнобочнаго именуемаго п… смотреть
ДИАГОНАЛЬ
diagonal* * *диагона́ль ж.
1. diagonal
2. (теоретического чертежа судна) diagonal [ribband] lineбольша́я диагона́ль — main diagonal (in magic square… смотреть
ДИАГОНАЛЬ
1) Орфографическая запись слова: диагональ2) Ударение в слове: диагон`аль3) Деление слова на слоги (перенос слова): диагональ4) Фонетическая транскрипц… смотреть
ДИАГОНАЛЬ
-и, ж.
1. мат.
Отрезок прямой, соединяющий вершины двух несмежных углов многоугольника или две вершины многогранника, не лежащие в одной плоскости.2…. смотреть
ДИАГОНАЛЬ
Нагло Льдина Лонг Логин Лог Лион Линь Линда Лина Лида Лиго Лиганд Лига Лиана Лань Ландо Ланда Лана Ладь Ладонь Ладога Ладо Ладно Ладан Лада Лад Лаг Ион Иол Инь Иногда Индол Инд Инга Илона Идол Идо Идальго Ида Иго Игла Донг Донага Дон Долина Долган Долг Дол Дог Дно Длина Длань Дион Диола Динго Динг Дин Диана Диалог Диагональ Дань Данио Данило Данил Дан Даль Гонд Гонада Гон Гольд Голь Нал Налог Гол Нгал Нил Нло Година Нога Год Гниль Гнида Глина Ноль Гланда Гладь Глад Гиль Гид Гиада Гдо Ода Одаль Ганоид Ганда Гана Олдь Галоид Гало Галиона Галина Гадина Гад Аонида Аналог Альгин Алин Аил Аида Адалин Ада Агад Ага Ольда Алан Алдан Англо Ангола Анда Анид Аноа Анод Аон Ольга Олин Гала… смотреть
ДИАГОНАЛЬ
Немецкое – Diagonale.Французское – diagonale.Латинское – diagonalis (диагональная линия).Слово «диагональ» пришло в русский язык из западноевропейских … смотреть
ДИАГОНАЛЬ
diagonal– большая диагональ– главная диагональ– диагональ определителя– пространственная диагональдоминирующая главная диагональ — dominant main diagon… смотреть
ДИАГОНАЛЬ
плотная ткань с рельефными наклонными рубчиками на лицевой стороне. Вырабатывается чистошерстяная, полушерстяная, хлопчатобумажная, шелковая, штапел… смотреть
ДИАГОНАЛЬ
köşegen; diyagonal* * *ж1) мат. köşegen; çapraz шахм.
2) (ткань) diyagonal
••по диагона́ли — verev (lemesine)Синонимы:
долонь, искосина, линия, спецди… смотреть
ДИАГОНАЛЬ
диагональНемецкое — Diagonale.Французское — diagonale.Латинское — diagonalis (диагональная линия).Слово «диагональ» пришло в русский язык из западноевр… смотреть
ДИАГОНАЛЬ
сущ. жен. родамат., текст.1. мат. отрезок прямой, соединяющей вершины противоположных углов многоугольника2. текст. ткань с косыми рубчикамидіагональ¤… смотреть
ДИАГОНАЛЬ
ДИАГОНАЛЬ диагонали, ж. (латин. diagonalis). 1. Прямая линия, соединяющая несмежные вершины многоугольника или многогранника (мат.). || То же спец. о прямой линии, соединяющей противоположные углы прямоугольника и расположенной под острым углом к его сторонам (мат.). 2. Ткань с рубчиками, идущими по косой линии. По диагонали — наискось, не под прямым углом. Перешел улицу по диагонали.<br><br><br>… смотреть
ДИАГОНАЛЬ
диагональ, диагон′аль, -и, ж.1. В математике: отрезок прямой линии, соединяющий две вершины многоугольника, не лежащие на одной стороне, или две вершин… смотреть
ДИАГОНАЛЬ
ДИАГОНАЛЬ, -и, ж. 1. В математике: отрезок прямой линии, соединяющий две вершины многоугольника, не лежащие на одной стороне, или две вершины многогранника, не лежащие на одной грани. 2. Ткань с косыми рубчиками. По диагонали — наискось, не под прямым углом. Разлиновать лист по диагонали. || прилагательное диагональный, -ая, -ое (к 1 значение) и диагоналевый, -ая, -ое (ко 2 значение)…. смотреть
ДИАГОНАЛЬ
ж.diagonal- главная диагональ матрицы- главная диагональ- диагональ грани куба- диагональ грани- диагональ куба- диагональ многогранника- диагональ мно… смотреть
ДИАГОНАЛЬ
ж. мат., текст.
diagonale fпо диагонали — en diagonale, diagonalementСинонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬ
корень — ДИАГОНАЛЬ; нулевое окончание;Основа слова: ДИАГОНАЛЬВычисленный способ образования слова: Бессуфиксальный или другой∩ — ДИАГОНАЛЬ; ⏰Слово Диаг… смотреть
ДИАГОНАЛЬ
(3 ж), Р., Д., Пр. диагона/ли; мн. диагона/ли, Р. диагона/лейСинонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬ
диагональ сущ.жен.неод. (1)
ед.им.
Настоящий город или Кале, к югу от предместия, в виде прямоугольника, которого диагональ плотно примыкает к Куре…. смотреть
ДИАГОНАЛЬ
ж. 1) матем. diagonale f 2) текст. diagonale f — главная диагональ- диагональ детерминанта
ДИАГОНАЛЬ
ДИАГОНАЛЬ ж. черта, соединяющая два угла, проведенная с угла на угол, в плоском угольнике или в теле; искосина, долонь. Долонь прямоуголыника делит его пополам, на два равные треугольника. | Род французского сукна, с косою низкою. Диагональный искосный, долонный; диагонально, долонью, искосиной, с угла на угол. <br><br><br>… смотреть
ДИАГОНАЛЬ
диагональ I
ж. мат.
диагональ (көп бурчтуктун тушташ эмес зки бурчун кошуучу түз сызык же көп кырдыктын бир тегиздикте жатпаган бурчтарын кошуучу түз сызык);
по диагонали кыйчалыш, кыйык;
перейти улицу по диагонали көчөдөн кыйык өтүү.
диагональ II
ж.
(ткань) диагональ (кыйык сүрөттүү кобулдары бар кездеме)…. смотреть
ДИАГОНАЛЬ
диагональ [лат. diagonalis < гр. diago-nios идущий от угла к углу] — 1) геом. отрезок прямой, соединяющий вершины двух углов многоугольника, не прилега… смотреть
ДИАГОНАЛЬ
жDiagonale fпо диагонали — schräg (наискось)Синонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬ
ж. мат., текст. diagonale f по диагонали — en diagonale, diagonalement
ДИАГОНАЛЬ
диагона́ль,
диагона́ли,
диагона́ли,
диагона́лей,
диагона́ли,
диагона́лям,
диагона́ль,
диагона́ли,
диагона́лью,
диагона́лями,
диагона́ли,
диагона́лях
(Источник: «Полная акцентуированная парадигма по А. А. Зализняку»)
.
Синонимы:
долонь, искосина, линия, спецдиагональ, ткань… смотреть
ДИАГОНАЛЬ
1) 对角线 duìjiǎoxiàn, 中斜线 zhōngxiéxiàn2) (ткань) 斜纹 布 xiéwénbù•- идти по диагонали — по диагоналиСинонимы:
долонь, искосина, линия, спецдиагональ, ткань… смотреть
ДИАГОНАЛЬ
Rzeczownik диагональ f Matematyczny przekątna f
ДИАГОНАЛЬ
(от греч. d идущий от угла к углу), отрезок прямой, соединяющий две несмежные вершины многоугольника или две вершины многогранника, не принадлежащие од… смотреть
ДИАГОНАЛЬ
Ударение в слове: диагон`альУдарение падает на букву: аБезударные гласные в слове: диагон`аль
ДИАГОНАЛЬ
1) мат. диагональ2) текст. диагональ (плотная ткань с рубчиками, идущими по косой линии) || диагоналевый;
пасьтавны важ диагональ гимнастёрка — одеть старую гимнастёрку из диагонали;сійӧ вӧлі лӧсталан диагональ гача — он был в лоснящихся диагоналевых брюках… смотреть
ДИАГОНАЛЬ
ж.diagonal fпо диагонали — en diagonal, diagonalmente
ДИАГОНАЛЬ
f.diagonalСинонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬ
ДИАГОНАЛЬ (от греч . diagonios — идущий от угла к углу), отрезок прямой, соединяющий две несмежные вершины многоугольника или две вершины многогранника, не принадлежащие одной грани.<br><br><br>… смотреть
ДИАГОНАЛЬ
матем.
діагона́ль, косина́
— диагональ многоугольника
— диагональ множества
— диагональ произведения
— побочная диагональ
Синонимы:
долонь, искосина, линия, спецдиагональ, ткань… смотреть
ДИАГОНАЛЬ
ДИАГОНАЛЬ (от греч. diagonios — идущий от угла к углу) — отрезок прямой, соединяющий две несмежные вершины многоугольника или две вершины многогранника, не принадлежащие одной грани.<br>… смотреть
ДИАГОНАЛЬ
ДИАГОНАЛЬ, плотная хлопчатобумажная или шерстяная ткань с отчетливо выраженными наклонными рубчиками. Из диагонали шьют воинское обмундирование, куртки и т. д.<br><br><br>… смотреть
ДИАГОНАЛЬ
диагональ диагона́льж., из франц. diagonale; см. Горяев, ЭС 4461.••1 У Горяева так: из лат. diagōn-āl-is (греч. διαγων-ια). — Прим. ред.
ДИАГОНАЛЬ
диагона́ль, -иСинонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬ
жdiagonal fСинонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬ
ДИАГОНАЛЬ — плотная хлопчатобумажная или шерстяная ткань с отчетливо выраженными наклонными рубчиками. Из диагонали шьют воинское обмундирование, куртки и т. д.<br>… смотреть
ДИАГОНАЛЬ
Ж diaqonal (1. riyaz. çoxbucaqlının və ya çoxüzlünün yanaşı olmayan təpələrini birləşdirən düz xətt; 2. toxuma milləri çəpinə gedən yun parça); по диагонали çəpinə…. смотреть
ДИАГОНАЛЬ
диагональ ж Diagonale f c по диагонали schräg (наискось)Синонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬ
ДИАГОНАЛЬ , плотная хлопчатобумажная или шерстяная ткань с отчетливо выраженными наклонными рубчиками. Из диагонали шьют воинское обмундирование, куртки и т. д…. смотреть
ДИАГОНАЛЬ
ДИАГОНАЛЬ, плотная хлопчатобумажная или шерстяная ткань с отчетливо выраженными наклонными рубчиками. Из диагонали шьют воинское обмундирование, куртки и т. д…. смотреть
ДИАГОНАЛЬ
диагон’аль, -иСинонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬ
kipert, kiper, muggСинонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬ
диагона’ль, диагона’ли, диагона’ли, диагона’лей, диагона’ли, диагона’лям, диагона’ль, диагона’ли, диагона’лью, диагона’лями, диагона’ли, диагона’лях
ДИАГОНАЛЬ
• diagonál• diagonála• příčka• úhlopříčka• úhlopříčna
ДИАГОНАЛЬ
átlóСинонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬ
אלכסוןאלכסונינטויСинонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬ
ж.
diagonale
по диагонали — in diagonale
Итальяно-русский словарь.2003.
Синонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬ
диагональDiagonaleСинонимы:
долонь, искосина, линия, спецдиагональ, ткань
ДИАГОНАЛЬ
диагональ = ж. 1. diagonal; 2. (материя) diagonal (cloth); по диагонали diagonally; диагональный diagonal.
ДИАГОНАЛЬ
ж., из франц. diagonale; см. Горяев, ЭС 4461.••1 У Горяева так: из лат. diagon-al-is (греч. -). — Прим. ред.
ДИАГОНАЛЬ
диагонал||ьж
1. мат ἡ διαγώνιος:
по ~и διαγώνια, διαγωνίως·
2. текст. τό ψαροκόκκαλο (ύφασμα).
ДИАГОНАЛЬ
Начальная форма — Диагональ, винительный падеж, единственное число, женский род, неодушевленное
ДИАГОНАЛЬ
Диагона́льmstari wa hanamu (mi-), kukata mraba, ulalo (ndalo)
ДИАГОНАЛЬ
жен. мат. дыяганаль, жен. текст. дыяганаль, муж.
ДИАГОНАЛЬ
I мат. диагональ, қиғаш сызықII текст, диагональ (бедері қиғаш тоқылған мата)
ДИАГОНАЛЬ
Диагональ- linea diagonalis; Диагонально — diagonaliter;
ДИАГОНАЛЬ
ж диагональ) △ по диагонали диагональ буенча. чапырыш, кыйгачлап
ДИАГОНАЛЬ
диагональ ж η διαγώνιος’ по ~и κατά διαγώνια κατεύ θυνση
ДИАГОНАЛЬ
II текст. диагональ. ДИАГОНАЛЬ I мат. диагональ.
ДИАГОНАЛЬ
діягоналя, косина, перекут, (реже) перекутня.
ДИАГОНАЛЬ
diagonāle; diagonālaudums, diagonāls
Диагональ прямоугольника – формула, длина
На чтение 2 мин Просмотров 22
В школьном курсе математики одной из первых в изучении фигур является прямоугольник. Диагональ прямоугольника участвует в решении многих задач. Поэтому имеет смысл подробнее рассмотреть этот элемент фигуры.
Определение
Прямоугольник является четырехугольником с равными углами и попарно равными и параллельными противоположными сторонами.
Поэтому диагональ будет делить данную геометрическую фигуру на два прямоугольных треугольника. Получается, что значение этого отрезка можно будет найти через корень квадратный суммы квадратов соответствующих сторон прямоугольника (по теореме Пифагора).
Диагональ прямоугольника обозначают маленьким латинским символом d или двумя заглавными буквами, по названию вершин, которые соединяет диагональ.
Длина диагонали прямоугольника, вокруг которого описана окружность, равняется диаметру этой окружности.
Рис. 1. Диагональ вписанного прямоугольника.
Это свойство может помочь в решении задач на нахождение сторон треугольника.
Характеристики понятия
Диагональ прямоугольника это отрезок, соединяющий вершины прямоугольника, находящиеся напротив друг друга. Рассматриваемый параметр можно найти, используя периметр основной геометрической фигуры, ее площадь или соотношение соответствующих сторон. Для этого используют формулу диагонали прямоугольника:
$d=sqrt{a^2+b^2}$, где а и b – стороны прямоугольника.
Рис. 2. Свойства прямоугольника
Значение
В математике различают свойства диагоналей прямоугольника. Так, эти отрезки пересекаются в одной точке, и точкой пересечения делятся пополам. В одном прямоугольнике диагонали будут равными.
Рис. 3. Диагональ прямоугольника.
На этом рисунке четко просматриваются углы, которые формируют диагонали.
Если диагонали параллелограмма равны, то эта геометрическая фигура является прямоугольником. Можно утверждать то же самое, когда сумма квадратов отрезков параллелограмма равна квадрату его диагонали (естественно речь идет о теореме Пифагора).
Что мы узнали?
Свойства диагонали прямоугольника используются для нахождения важных параметров этой фигуры. Решения задач, в которых требуется доказать наличие определенного типа четырехугольника нередко рассматривают диагонали параллелограмма. С помощью данных отрезков можно найти площадь фигуры, которой они принадлежат.
Беликова Ирина
Учитель физики, информатики и вычислительной техники. Победитель конкурса лучших учителей Российской Федерации в рамках Приоритетного Национального Проекта «Образование».
В математике, диагональ имеет геометрический смысл, а также используется в терминах квадратных матриц.
Файл:Diagonals.svg Шестиугольник с диагоналями
Многоугольники
Для многоугольников, диагональ это отрезок, соединяющий две вершины, не лежащие на одной стороне. Так, четырёхугольник имеет две диагонали, соединяющие противолежащие вершины. У выпуклого многоугольника диагонали проходят внутри него. Это не выполняется для самопересекающихся многоугольников. Многоугольник выпуклый тогда и только тогда, когда его диагонали лежат внутри.
Пусть n — число вершин многоугольника, вычислим d — число возможных разных диагоналей. Каждая вершина соединена диагоналями со всеми другими вершинами, кроме двух соседних и, естественно, себя самой. Таким образом, из одной вершины можно провести n-3 диагонали; перемножим это на число вершин
- (n − 3) × n,
однако, мы посчитали каждую диагональ дважды (по разу для каждого конца) — отсюда,
Матрицы
В случае с квадратными матрицами, главная диагональ является диагональной линией элементов, которая проходит с северо-запада на юго-восток. Например, единичная матрица может быть описана, как матрица, имеющая единицы на главной диагонали и нули вне её. Диагональ с юго-запада на северо-восток часто называется побочная диагональ. Наддиагональными элементами называются такие, что лежат выше и правее главной диагонали. Поддиагональными — те, что ниже и левее. Диагональная матрица — такая матрица, у которой все элементы вне главной диагонали равны нулю.
Формула расчета диагонали квадрата — дополнить статью…
Теория множеств
По аналогии, подмножество декартового произведения X×X произвольного множества X на само себя, состоящее из пар элементов (x, x), называется диагональю множества. Это — единичное отношение, оно играет важную роль в геометрии: например, константные элементы отображения F с X в X могут быть получены сечением F с диагональю множества X.
Внешние ссылки.
- Диагонали многоугольникка с интерактивными анимациями
- Диагонали многоугольника с MathWorld.
- Диагонали матриц от MathWorld.
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Диагональ. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
В геометрия, а диагональ это отрезок присоединение двух вершины из многоугольник или же многогранник, когда эти вершины не находятся на одной край. Неформально любую наклонную линию называют диагональной. Слово диагональ происходит от древнегреческий διαγώνιος диагони,[1] «от угла к углу» (от διά- диа-, «через», «поперек» и γωνία гония, «угол», относящийся к угрюмый «колено»); его использовали оба Страбон[2] и Евклид[3] для обозначения линии, соединяющей две вершины ромб или же кубовид,[4] и позже принят на латынь как диагонус («косая линия»).
В матричная алгебра, диагональ квадрата матрица представляет собой набор записей, простирающихся от одного до самого дальнего угла.
Есть и другие нематематические применения.
Нематематическое использование
Стенд основных строительных лесов на строительной площадке дома с диагональными распорками для сохранения конструкции.
В инженерное дело, диагональная скоба — это балка, используемая для крепления прямоугольной конструкции (например, строительные леса ) выдерживать толчки сильных сил; хотя диагональные скобы называются диагональными, из практических соображений они часто не соединяются с углами прямоугольника.
Плоскогубцы диагональные Кусачки для проволоки, определяемые режущими кромками губок, пересекающими стыковочную заклепку под углом или «по диагонали», отсюда и название.
А диагональная увязка это тип найтовки, используемой для связывания лонжеронов или стоек вместе, применяемых таким образом, чтобы найтовки пересекали стойки под углом.
В ассоциация футбола, то диагональ система контроля — это метод, который используют судьи и помощники судьи для позиционирования себя в одном из четырех квадрантов поля.
Полигоны
Применительно к многоугольник, диагональ — это отрезок соединение любых двух непоследовательных вершин. Следовательно, четырехугольник имеет две диагонали, соединяющие противоположные пары вершин. Для любого выпуклый многоугольник, все диагонали лежат внутри многоугольника, но для повторно входящие многоугольники, некоторые диагонали находятся за пределами многоугольника.
Любой п-сторонний многоугольник (п ≥ 3), выпуклый или же вогнутый, имеет 
|
|
|
|
|
Области, образованные диагоналями
В выпуклый многоугольник, если нет трех диагоналей одновременный в одной точке внутри, количество регионов, на которые диагонали делят интерьер, определяется как
За п-угольники с п= 3, 4, … количество регионов равно[5]
- 1, 4, 11, 25, 50, 91, 154, 246…
Это OEIS последовательность A006522.[6]
Пересечения диагоналей
Если никакие три диагонали выпуклого многоугольника не совпадают во внутренней точке, количество внутренних пересечений диагоналей определяется как 
Правильные многоугольники
А треугольник не имеет диагоналей.
А квадрат имеет две диагонали равной длины, которые пересекаются в центре квадрата. Отношение диагонали к стороне равно
А правильный пятиугольник имеет пять диагоналей одинаковой длины. Отношение диагонали к стороне — это Золотое сечение,
Обычный шестиугольник имеет девять диагоналей: шесть более коротких равны друг другу по длине; три более длинных равны друг другу по длине и пересекаются в центре шестиугольника. Отношение длинной диагонали к стороне равно 2, а отношение короткой диагонали к стороне равно 
Обычный семиугольник имеет 14 диагоналей. Семь более коротких равны друг другу, а семь более длинных равны друг другу. Обратная сторона равна сумме обратных величин короткой и длинной диагонали.
В любом регулярном п-гон с п даже все длинные диагонали пересекают друг друга в центре многоугольника.
Многогранники
А многогранник (а твердый объект в трехмерное пространство, ограниченный двумерный лица ) может иметь два разных типа диагоналей: диагонали лица на разных гранях, соединяя несмежные вершины на одной грани; и диагонали пространства, полностью внутри многогранника (за исключением концов на вершинах).
Так же как треугольник не имеет диагоналей, поэтому тетраэдр (с четырьмя треугольными гранями) не имеет диагоналей граней и пространственных диагоналей.
А кубовид имеет две диагонали на каждой из шести граней и четыре диагонали пространства.
Матрицы
В случае квадратная матрица, то главный или же главная диагональ — диагональная линия записей, идущая от верхнего левого угла к нижнему правому углу.[9][10][11] Для матрицы 




Диагональ от верхнего правого до нижнего левого угла иногда описывается как незначительный диагональ или антидиагональный. В недиагональный записи не на главной диагонали. А диагональная матрица это тот, у которого все недиагональные элементы равны нулю.[12][13]
А супердиагональ вход — это тот, который находится прямо над и справа от главной диагонали.[14][15] Так же, как диагональные записи 


Точно так же субдиагональный вход — это тот, который находится непосредственно под и слева от главной диагонали, то есть запись 








Геометрия
По аналогии подмножество из Декартово произведение Икс×Икс любого набора Икс с самим собой, состоящий из всех пар (x, x), называется диагональю и является график из равенство связь на Икс или, что то же самое, график из функция идентичности из Икс к Икс. Это играет важную роль в геометрии; например, фиксированные точки из отображение F из Икс самому себе может быть получена пересечением графика F с диагональю.
В геометрических исследованиях идея пересечения диагонали с собой является обычным явлением, не напрямую, а путем нарушения его в пределах класс эквивалентности. Это связано на глубоком уровне с Эйлерова характеристика и нули векторные поля. Например, круг S1 имеет Бетти числа 1, 1, 0, 0, 0, и, следовательно, эйлерова характеристика 0. Геометрический способ выразить это — взглянуть на диагональ на двухугольнике.тор S1xS1 и заметьте, что он может двигаться от себя малым движением (θ, θ) к (θ, θ + ε). В общем, число пересечения графика функции с диагональю может быть вычислено с использованием гомологии через Теорема Лефшеца о неподвижной точке; самопересечение диагонали является частным случаем тождественной функции.
Смотрите также
- Нормальная форма Джордана
- Главная диагональ
- Диагональный функтор
Примечания
- ^ Интернет-словарь этимологии
- ^ Страбон, География 2.1.36–37
- ^ Евклид, Книга Элементов 11, предложение 28
- ^ Евклид, Книга Элементов 11, предложение 38
- ^ Вайсштейн, Эрик В. «Диагональ многоугольника». Материал из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/PolygonDiagonal.html
- ^ Слоан, Н. Дж. А. (ред.). «Последовательность A006522». В Он-лайн энциклопедия целочисленных последовательностей. Фонд OEIS.
- ^ Пунен, Бьорн; Рубинштейн, Михаил. «Количество точек пересечения диагоналями правильного многоугольника». SIAM J. Дискретная математика. 11 (1998), нет. 1, 135–156; ссылка на версию на сайте Poonen
- ^ [1], начало в 2:10
- ^ Бронсон (1970, п. 2)
- ^ Герштейн (1964, п. 239)
- ^ Неринг (1970 г., п. 38)
- ^ Герштейн (1964, п. 239)
- ^ Неринг (1970 г., п. 38)
- ^ Бронсон (1970, стр. 203,205)
- ^ Герштейн (1964, п. 239)
- ^ Каллен (1966), п. 114)
Рекомендации
- Бронсон, Ричард (1970), Матричные методы: введение, Нью-Йорк: Академическая пресса, LCCN 70097490
- Каллен, Чарльз Г. (1966), Матрицы и линейные преобразования, Чтение: Эддисон-Уэсли, LCCN 66021267
- Герштейн, И. Н. (1964), Темы по алгебре, Уолтем: Издательство Blaisdell, ISBN 978-1114541016
- Неринг, Эвар Д. (1970), Линейная алгебра и теория матриц (2-е изд.), Нью-Йорк: Wiley, LCCN 76091646
внешняя ссылка
- Диагонали многоугольника с интерактивной анимацией
- Диагональ многоугольника из MathWorld.
- Диагональ матрицы из MathWorld.











 ,
,