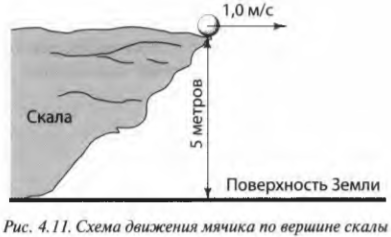
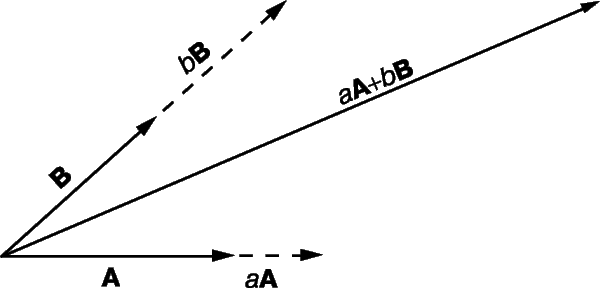
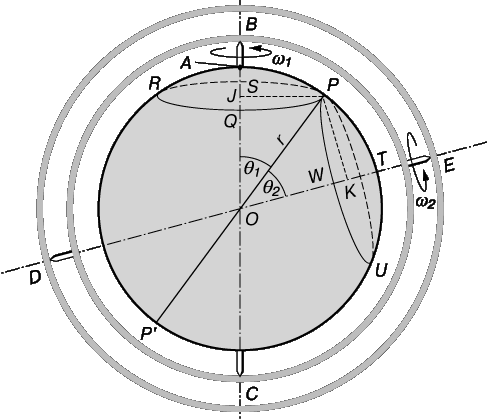
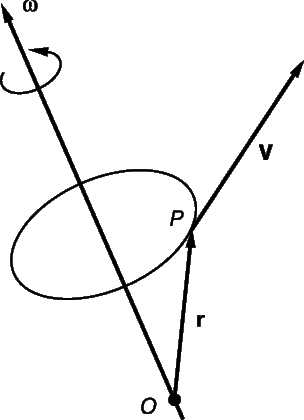
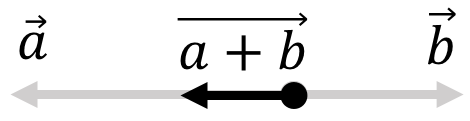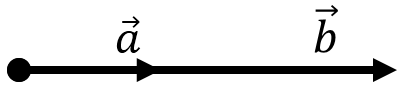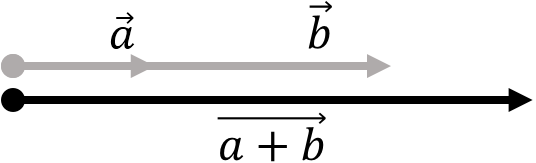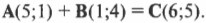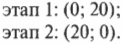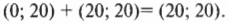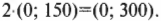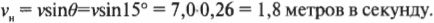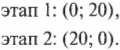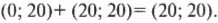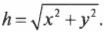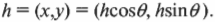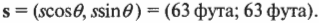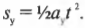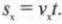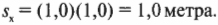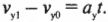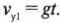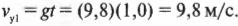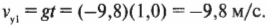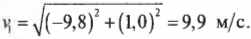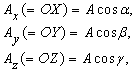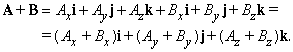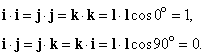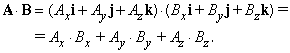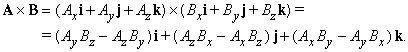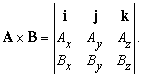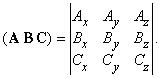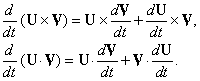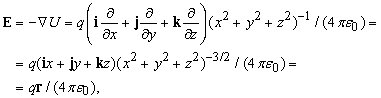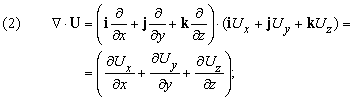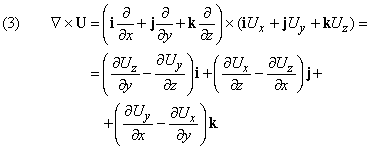Векторы – основные понятия и формулы
На прошлом занятии мы разобрались с основными определениями кинематики.
И ты наверняка обратил внимание, что некоторые величины имеют только значение (число) – например, путь ((L)).
А некоторые имеют и число, и направление – например, перемещение ((vec{S})).
И сейчас ты узнаешь, почему это настолько важно.
Векторы – коротко о главном
- Существуют скалярные величины: они имеют значение, но не имеют направления;
- Существуют векторные величины. Они имеют как значение, так и направление;
- Значение вектора есть его длина;
- Для большинства операций над векторами необходим пареллельный перенос;
- Вектор можно умножать на скаляр;
- Нулевой вектор – вектор, начало которого совпадает с концом;
- Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых;
- Коллинеарные векторы, имеющие одинаковую длину и противоположные направления, называются обратными друг другу;
- Векторы можно складывать и вычитать разными методами;
- Правило параллелограмма действует как для сложения, так и для вычитания векторов;
- Векторы можно умножать друг на друга двумя различными способами: скалярным и векторным;
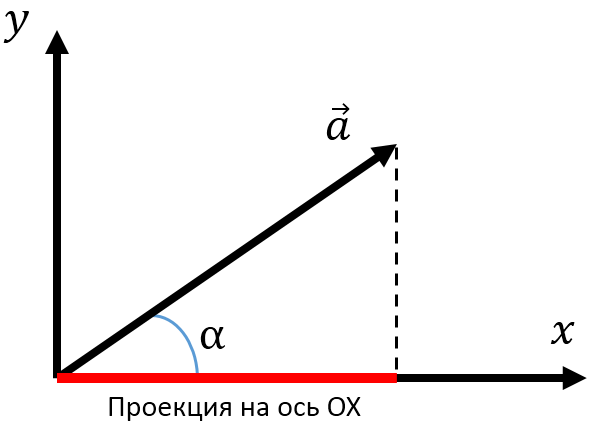
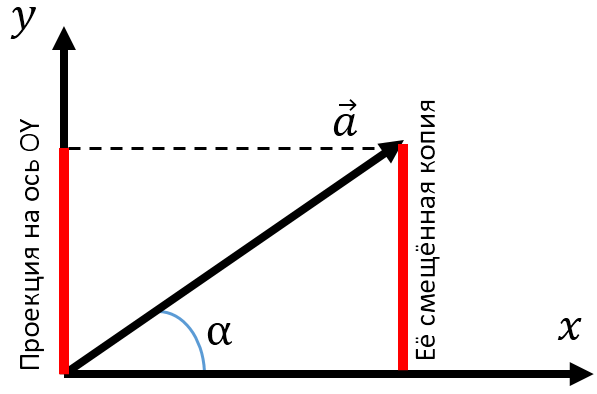
- Проекция вектора на ось — разность между координатами проекций точек конца и начала вектора на ось;
- Если вектор направлен туда же, куда и ось, его проекция положительна. Если вектор направлен в другую сторону, его проекция отрицательна;
- Вектор сам по себе не может быть отрицательным;
- Длина вектора так же не может быть отрицательной;
- Проекция вектора бывает отрицательной;
- Над проекциями тоже можно совершать действия, и это удобнее, чем работать с векторами;
- Проекция суммы векторов равна сумме проекций векторов;
- Проекция разности векторов равна разности проекций векторов;
- С проекцией вектора можно работать как с числом;
Решать задачи с векторами — легко!
Векторы и… Колумб
В 1492 году Колумб приказал кораблям изменить курс на запад-юго-запад, полагая, что он и его команда уже прошли мимо Японии, не заметив ее островов.
Вскоре его экспедиция наткнулась на множество архипелагов, которые ошибочно принимали за земли Восточной Азии. И теперь, спустя века, американцы в октябре отмечают высадку Колумба в Новом Свете.
Кто знает, как повернулась бы история, если бы его корабли не поменяли свое направление?
О направлении
Направление – одна из важнейших характеристик движения.
Подумай, какие из этих величин являются просто числами, а какие тоже являются числами, но имеют еще и направление.
- сила;
- время;
- скорость;
- длина;
- перемещение;
- масса;
- температура;
Наверное, ты без труда заметил, что направление имеют сила, скорость, перемещение, а время, длина, масса и температура – это просто числа.
Так вот, «просто числа» – это скалярные величины (их также называют скалярами).
А «числа с направлением» – это векторные величины (их иногда называют векторы).
В физике существует множество скалярных и векторных величин.
Что такое скалярная величина?
Скалярная величина, в отличие от вектора, не имеет направления и определяется лишь значением (числом)
Это, например, время, длина, масса, температура (продолжи сам!)
Что такое векторная величина?
Векторная величина – это величина, которая определяется и значением, и направлением.
В случае с векторами нам важно, куда мы, например, тянем груз или в какую сторону движемся.
Например, как на этом рисунке изображен вектор силы (нам важно не только с какой силой, но и куда мы тянем груз):
Как обозначаются векторы?
Векторы принято обозначать специальным символом – стрелочкой над названием. Вот, например, вектор перемещения: (vec{S})
Значение вектора – это модуль вектора, то есть его длина.
Обозначить это можно двумя способами: (left| {vec{S}} right|) или (S)
Операции над векторами
Для решения задач необходимо уметь работать с векторами: складывать, вычитать, умножать их.
Давай научимся это делать. Мы пойдем от простого к сложному, но это вовсе не значит, что будет трудно!
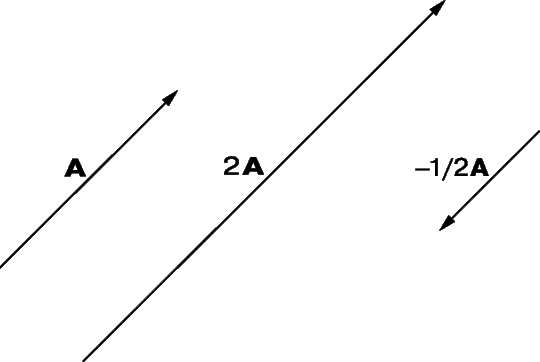
Умножение вектора на число
Если вектор умножить на какое-либо число (скаляр), мы просто «растягиваем» вектор, сохраняя его направление. Получившийся вектор сонаправлен начальному, то есть они имеют одинаковое направление.
Это обозначается так: (vec{a}uparrow uparrow vec{b})
(Если направление противоположно, обозначаем так: (vec{a}uparrow downarrow vec{b}))
Рассмотрим на примере, используя клетку для точности построений:
Если вектор умножить на ноль, он станет нулевым.
Обязательно нужно ставить значок вектора над нулем! Нельзя говорить, что векторная величина просто равна скалярной:
(vec{c}=0cdot vec{a}Rightarrow vec{c}=vec{0})
Рассмотрим некоторые свойства нулевого вектора.
Если он нулевой, то его длина равна нулю! Логично, не правда ли?
А это значит, что его начало совпадает с концом, это просто какая-то точка.
Нулевой вектор – вектор, начало которого совпадает с концом.
Нулевой вектор принято считать сонаправленным любому вектору.
Его мы можем получить не только путем умножения вектора на ноль, но и путем сложения противонаправленных векторов:
(vec{a}+(-vec{a})=vec{0})
А если к любому вектору прибавит нулевой, ничего не изменится:
(vec{a}+vec{0}=vec{a})
Если вектор умножают на отрицательное число, он изменит свое направление на противоположное. Такой вектор называется обратным данному.
Но такие векторы должны быть коллинеарны. Звучит как скороговорка, но ничего страшного. Главное – понять суть.
Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых.
Две прямые параллельны: (qparallel p)
Векторы лежат на одной прямой: они коллинеарны. По направлению видно, что они противонаправлены, это обозначается так:
(vec{a}uparrow downarrow vec{c})
Векторы лежат на параллельных прямых, они коллинеарны. При этом они сонаправлены:
(vec{a}uparrow uparrow vec{b})
Эти двое тоже коллинеарны! Они ведь лежат на параллельных прямых. При этом они противонаправлены:
(vec{b}uparrow downarrow vec{c})
Коллинеарные векторы, имеющие одинаковую длину и противоположные направления, называются обратными друг другу.
Параллельный перенос векторов
Одно из важных свойств вектора, которое очень часто помогает в операциях над ним, – параллельный перенос.
Если передвинуть вектор, не меняя его направления и длины, он будет идентичен начальному. Это свойство – параллельный перенос.
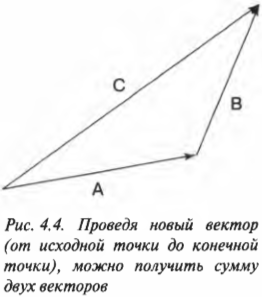
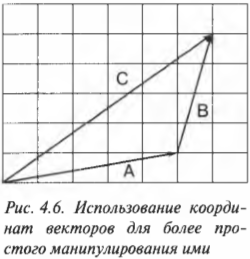
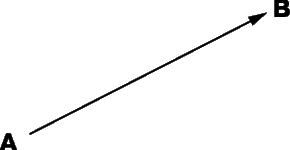
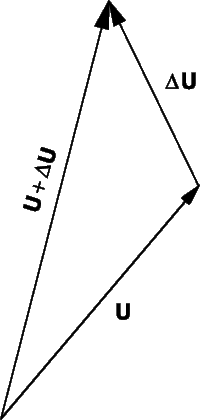
Сложение векторов по правилу треугольника
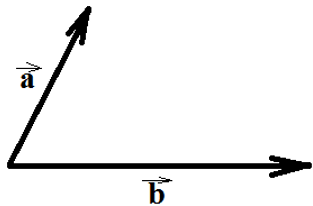
Сложение векторов – одна из самых легких и приятных вещей. Предположим, у нас есть два вектора:
Наша цель – найти такой вектор, который будет являться суммой двух данных:
(vec{c}=vec{a}+vec{b})
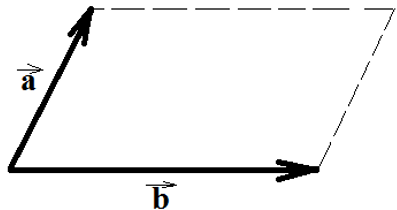
Для начала нужно сделать так, чтобы конец одного вектора был началом другого. Для этого воспользуемся параллельным переносом:
Теперь достроим до треугольника.
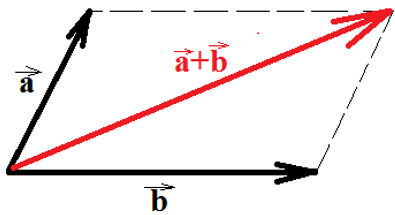
Но как узнать направление нужного нам вектора?
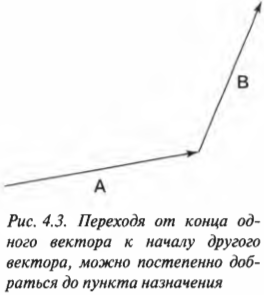
Все просто: вектор суммы идет от начала первого слагаемого к концу второго, мы словно «идём» по векторам:
Это называется правилом треугольника.
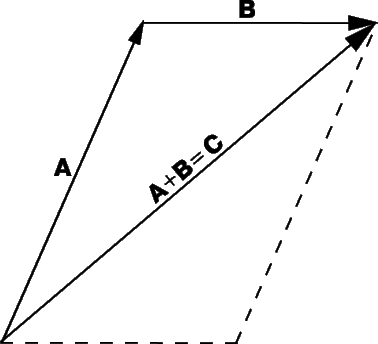
Больше двух слагаемых векторов. Сложение по правилу многоугольника
Но что делать, нам нужно сложить не два, а три, пять векторов или даже больше?
Мы руководствуемся той же логикой: соединяем векторы и «идём» по ним:
(vec{e}=vec{a}+vec{b}+vec{c}+vec{d})
Это называется правилом многоугольника.
Вычитание векторов через сложение
Вычитание векторов не сложнее. Это даже можно сделать через сумму! Для этого нам понадобится понятие обратного вектора. Запишем разность так:
(vec{c}=vec{a}-vec{b}=vec{a}+(-vec{b}))
Тогда нам лишь остается найти сумму с обратным вектором:
А сделать это очень легко по правилу треугольника:
Всегда помни, что вычитание можно представлять сложением, а деление — умножением на дробь.
Вычитание векторов через треугольник
Вычитать векторы можно через треугольник. Основная задача будет состоять в том, чтобы определить направление вектора разности.
Итак, векторы должны выходить из одной точки. Далее мы достраиваем рисунок до треугольника и определяем положение. Рассмотрим два случая:
(vec{c}=vec{a}-vec{b})
(vec{c}=vec{b}-vec{a})
Направление вектора разности зависит от того, из какого вектора мы вычитаем. У них совпадают концы.
Универсальное правило параллелограмма
Есть еще один способ сложения и вычитания векторов.
Способ параллелограмма наиболее востребован в физике и сейчас ты поймешь, почему. Основа в том, чтобы векторы выходили из одной точки, имели одинаковое начало.
Вот так:
Ничего не напоминает?
Именно! Когда мы делаем чертеж к задачам по физике, все силы, приложенные к телу, мы рисуем из одной точки.
В чем же заключается правило параллелограмма? С помощью параллельного переноса достроим до параллелограмма:
Тогда вектор суммы будет диагональю этой фигуры. Это легко проверяется правилом треугольника. Начало этого вектора совпадает с началом двух слагаемых векторов:
Другая диагональ будет являться разностью этих векторов. Направление определяем так же, как делали раньше.
(vec{c}=vec{a}+vec{b})
(vec{d}=vec{a}-vec{b})
Векторное произведение векторов
Векторное произведение векторов пригодится нам в электродинамике.
Его формула лишь немного отличается от предыдущей:
(vec{a}times vec{b}=left| {vec{a}} right|cdot left| {vec{b}} right|cdot sin varphi )
В отличие от скалярного произведения, результатом его является вектор и его даже можно изобразить!
После параллельного переноса векторов и нахождения угла между ними достроим их до параллелограмма и найдем его площадь. Площадь параллелограмма равна длине вектора произведения:
Этот вектор одновременно перпендикулярен двум другим. Его направление зависит от условного порядка векторов, который либо определен какими-то фактами (когда мы будем изучать силу Лоренца), либо является свободным.
Об этом мы поговорим подробнее, когда будем изучать электродинамику.
Итак, мы разобрали операции с векторами, рассмотрев даже самые сложные из них. Это было не так тяжело, верно? Так происходит не только с векторами, но и со многими другими темами. Идя от легкого к сложному, мы даже не заметили трудностей.
Ведь всегда стоит помнить о том, что даже самое длинное путешествие начинается с первого шага.
Проекции векторов
Что такое проекция вектора и с чем ее едят?
Мы уже выяснили, что над векторами можно проводить множество операций. Здорово, когда можешь начертить векторы, достроить их до треугольника и измерить результат линейкой.
Но зачастую физика не дает нам легких цифр. Наша задача – не отчаиваться и быть умнее, упрощая себе задачи.
Для того, чтобы работать с векторами как с числами и не переживать об их положении и о точности рисунков, были придуманы проекции.
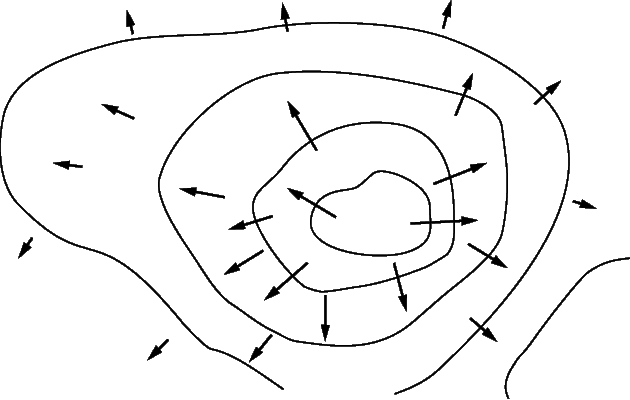
Проекция вектора – словно тень, которую он отбрасывает на ось координат. И эта тень может о многом рассказать.
Ось координат — прямая с указанными на ней направлением, началом отсчёта и выбранной единицей масштаба.
Ось можно выбрать произвольно. В зависимости от ее выбора можно либо значительно упростить решение задачи, либо сделать его очень сложным.
Именно поэтому необходимо научиться работать с проекциями и осями.
Построение проекции. Определение знака
Возьмем вектор и начертим рядом с ним произвольную ось. Назвать ее тоже можно как угодно, но мы назовем ее осью Х.
Теперь опустим из начала и конца вектора перпендикуляры на эту ось. Отметим координаты начала (Х0) и конца (Х). Рассмотрим отрезок, заключенный между этими точками.
Казалось бы, мы нашли проекцию. Однако думать, что проекция является простым отрезком, – большое заблуждение.
Не все так просто: проекция может быть не только положительной. Чтобы найти проекцию, нужно из координаты конца вычесть координату начала:
({{a}_{x}}=x-{{x}_{0}})
Проекция вектора на ось — разность между координатами проекций точек конца и начала вектора на ось.
Проекция обозначается так:
({{a}_{x}}), где a – название вектора, х – название оси, на которую проецируется вектор.
В случае выше определить знак довольно легко. Сразу видим, что координата конца численно больше координаты начала и делаем вывод о том, что проекция положительна:
(x>{{x}_{0}}Rightarrow {{a}_{x}}>0)
Порой работать с буквами трудно. Поэтому предлагаю взять конкретный пример:
Рассмотрим другой случай. В этот раз координата начала больше координаты конца, следовательно, проекция отрицательна:
(x<{{x}_{0}}Rightarrow {{b}_{x}}<0)
Пример на конкретных числах:
Рассмотрим еще один интересный случай.
Давай разместим ось так, чтобы вектор был ей перпендикулярен. Проекции точек начала и конца совпадут и проекция вектора будет равна нулю!
(x={{x}_{0}}Rightarrow {{c}_{x}}=0)
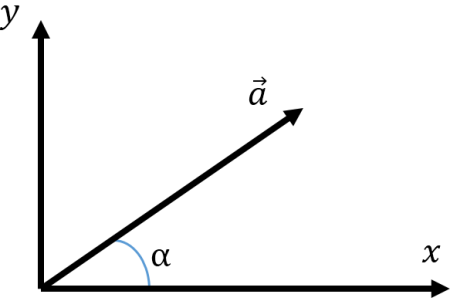
Анализ углов
Рассматривая эти ситуации, можно заметить, что знак, который принимает проекция вектора напрямую зависит от угла между вектором и осью, то есть от его направления!
Из начала вектора проведем луч, параллельный оси и направленный в ту же сторону, что и ось. Получим угол между вектором и осью.
Если угол острый, проекция положительна:
(alpha <{{90}^{o}}Rightarrow {{a}_{x}}>0)
Если угол тупой, проекция отрицательна:
(beta >{{90}^{o}}Rightarrow {{b}_{x}}<0)
Если угол прямой, она равна нулю:
(gamma ={{90}^{o}}Rightarrow {{c}_{x}}>0)
Обрати особое внимание на то, какой именно угол является углом между вектором и осью!
Частные случаи проекции
Настоящий подарок судьбы – тот момент, когда вектор параллелен оси. Это сохраняет драгоценное время при решении множества задач. Рассмотрим эти случаи.
Если вектор параллелен оси, угол между ними либо равен нулю, либо является развернутым (180О). Это зависит от направления.
При этом длина проекции совпадает с длиной вектора! Смотри!
Как и прежде, если вектор направлен туда же, куда и ось, проекция положительна:
(alpha ={{0}^{o}}Rightarrow {{a}_{x}}=a)
Если вектор направлен в другую сторону, проекция отрицательна:
(alpha ={{180}^{o}}Rightarrow {{a}_{x}}=-a)
Если вектор направлен туда же, куда и ось, его проекция положительна. Если вектор направлен в другую сторону, его проекция отрицательна.
Эти утверждения применимы не только к векторам, которые параллельны оси. Это особенно удобно использовать в тех случаях, когда ось направлена под углом.
Что? Почему раньше не сказал? А… Ну…
Хватит вопросов! Вот тебе пример:
(vec{a}) направлен в ту же сторону, что и ось. Его проекция положительна.
(vec{b}) направлен противоположно оси. Его проекция отрицательна.
Еще один частный случай – работа с обратными векторами.
Давай выясним, как связаны проекции данного вектора и вектора, который является ему обратным. Начертим их и обозначим координаты начал и концов:
Проведем дополнительные линии и рассмотрим два получившихся треугольника. Они прямоугольны, так как проекция строится с помощью перпендикуляра к оси.
Наши векторы отличаются лишь направлением. При этом, если мы просто посмотрим на них как на прямые, мы можем сказать, что они параллельны. Их длины тоже одинаковы.
Прямоугольные треугольники равны по углу и гипотенузе. Это значит, что численно равны и их катеты, в том числе те, которые равны проекциям:
(vec{a}’=-vec{a}) — векторы обратны друг другу;
(left| {vec{a}} right|=left| vec{a}’ right|) — равенство длин векторов;
Мы помним, что обратные векторы всегда коллинеарны. Это значит, что прямые, на которых они расположены, находятся под одним углом к оси:
(alpha =alpha ‘)
Остается лишь определиться со знаками. Данный вектор направлен по оси Х, а обратный ему – против. Значит, первый положителен, а второй отрицателен. Но модули их равны, так как равны их длины.
({{a}_{x}}=-a_{x}^{‘})
Проекции обратных векторов равны по модулю и противоположны по знаку.
Давайте еще раз уточним.
Вектор сам по себе не может быть отрицательным (обратный вектор есть вектор, умноженный на минус единицу).
Длина вектора так же не может быть отрицательной. Длина есть модуль вектора, а модуль всегда положителен.
Проекция вектора бывает отрицательной. Это зависит от направления вектора.
Способы нахождения проекций и векторов с помощью тригонометрии
Зная угол между вектором и осью, можно не прибегать к координатам. Углы, прямоугольные треугольники… Всегда стоит помнить, что, если ты видишь прямоугольный трегольник, тригонометрия протянет тебе руку помощи.
Именно тригонометрия чаще всего применяется в задачах, где требуется работать с проекциями. Особенно она помогает в задачах на второй закон Ньютона.
Рассмотрим вектор и его проекции на оси:
Можем заметить, что проекции вектора соответствуют катетам прямоугольного треугольника, который легко можно достроить:
Тогда обозначим прямой угол и угол между вектором и осью:
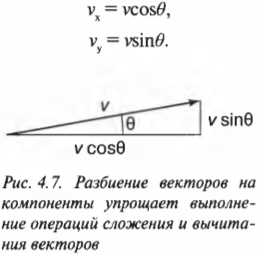
Зная, что проекции соответствуют катетам, мы можем записать, чему равны синус и косинус угла. Они равны отношению проекций к гипотенузе. За гипотенузу считаем длину данного вектора.
Из этих уравнений легко выражаются проекции.
(sin alpha =frac{{{a}_{y}}}{a})
(cos alpha =frac{{{a}_{x}}}{a})
А еще следует помнить, что из проекций мы можем найти длину данного вектора с помощью теоремы Пифагора:
({{a}^{2}}=a_{x}^{2}+a_{y}^{2})
Зная, как работать с проекциями векторов и часто практикуясь, можно довести свои навыки решения большинства задач механики до совершенства.
Действия над проекциями векторов. Решение задач
Умение применять свои знания на практике невероятно важны. Это касается не только физики.
Мы знаем, что проекции были придуманы для того, чтобы работать не с векторами, а с числами.
Давай попробуем.
Сложение проекций. Доказательство главного свойства
Предположим, у нас есть два вектора и нам нужно найти их сумму. Посчитать по клеткам нам вряд ли удастся:
Спроецируем оба вектора на ось Х. Заметим, что конец одного вектора есть начало второго, то есть их координаты совпадают:
Давай посчитаем проекции векторов и проекцию вектора их суммы:
Мы можем заметить, что сумма проекций двух данных векторов оказалась равна проекции вектора их суммы!
Намного важнее уметь доказывать гипотезы в общем виде.
Тогда никто не сможет упрекнуть тебя в том, что твои утверждения – просто результат совпадения!
Согласно определению проекции, запишем уравнения проекций для двух данных векторов и вектора их суммы:
Заметим, что некоторые точки совпадают. Начало (vec{a}) совпадает с началом (vec{c}). Как мы заметили ранее, конец (vec{a}) совпадает с началом (vec{b}). А конец (vec{b}) совпадает с концом (vec{c}).
Затем запишем, чему равна сумма этих векторов.
Видим, что конец (vec{a}) и начало (vec{b}) одинаковы. Поэтому избавимся от повторов:
У нас остались лишь начало (vec{a}) и конец (vec{b}). А это в свою очередь начало и конец (vec{c})!
Мы доказали нашу гипотезу.
Но что насчет разности?
Все очень просто! Помнишь, как мы считали разность через сумму? Здесь это делается аналогично!
Таким образом,
Проекция суммы векторов равна сумме проекций векторов.
Проекция разности векторов равна разности проекций векторов.
Или можно записать так:
(vec{c}=vec{a}pm vec{b}Rightarrow {{c}_{x}}={{a}_{x}}pm {{b}_{x}})
Простейшие задачи на нахождение проекций
Простейшие задачи на нахождение проекций чаще представлены в виде различных графиков или рисунков.
Давай научимся с ними работать.
Нам даны оси и векторы. Задача: найти проекции каждого из них на обе оси.
Будем делать все по порядку. Для каждого вектора предлагаю сначала определить знак проекций, а затем посчитать их.
В первом случае вектор направлен против оси Х.
Значит, его проекция на эту ось будет отрицательна. Мы убедимся в этом с помощью вычислений.
Сразу бросается в глаза то, что вектор расположен перпендикулярно оси Y. Его проекция на эту ось будет равна нулю, ведь расстояние между проекциями точек начала и конца равно нулю!
Рассмотрим второй вектор.
Он «сонаправлен» оси Y и «противонаправлен» оси Х. Значит, проекция на ось будет положительна, а на ось Х – отрицательна.
Убедимся в этом.
На осях для удобства отметим проекции точек начала и конца вектора, проведя перпендикуляры. Затем проведем вычисления:
Рассмотрим (vec{c}). Заметим, что он является обратным для (vec{b}): их длины равны, а направления противоположны.
Мы помним, что в таком случае их проекции отличаются лишь знаками. И это действительно так:
Поступаем с (vec{d}) так же, как поступали с первым вектором.
Он перпендикулярен оси Х, а значит его проекция (что есть разность между проекциями точки конца и начала!) на эту ось равна нулю.
Проведя перпендикуляры, считаем проекцию на ось Y:
С (vec{e}) работать приятно: он расположен по направлению обеих осей. Обе его проекции будут положительны, остается лишь посчитать их:
Задачи на нахождение вектора и его угла с осью
С помощью проекций можно найти длину вектора и его направление, а также угол, под которым он находится относительно оси.
Давай попробуем это сделать.
Даны проекции вектора на две оси. Для начала нарисуем оси:
Расположить вектор можно как угодно, поэтому произвольно отметим на осях его проекции. Мы помним, что проекции и вектор образуют прямоугольный треугольник. Давай попробуем его составить.
С проекцией на ось Х все понятно, просто поднимаем ее. Но куда поставить проекцию оси Y?
Для этого нам нужно определить направление вектора. Проекция на ось Х отрицательна, значит вектор направлен в другую сторону от оси.
Проекция на ось Y положительна. Вектор смотрит в ту же сторону, что и ось.
Исходя из этого, мы можем нарисовать вектор и получить прямоугольный треугольник:
Теперь нужно найти длину этого вектора. Используем старую добрую теорему Пифагора:
Обозначим угол (alpha ), который необходимо найти, мы учились это делать в начале изучения проекций. Он расположен вне треугольника. Мы ведь не ищем легких путей, верно?
Рассмотрим смежный ему угол (beta ). Его найти гораздо проще, а в сумме они дадут 180 градусов.
Чтобы сделать это, абстрагируемся от векторов, проекций и просто поработаем с треугольником, стороны которого равны 3, 4 и 5. Найдем синус угла (beta ) и по таблице Брадиса (либо с помощью инженерного калькулятора) определим его значение.
Вычитанием угла (beta ) из 180 градусов найдем угол (alpha ):
Главный метод работы с осями и проекциями в решении физических задач
В большинстве задач по физике, когда в условиях нам дают значения векторных величин, например, скорости, нам дают длину вектора.
Поэтому важно научиться искать проекции вектора и связывать их с ней.
Рассмотрим следующий рисунок (вектор F2 перпендикулярен вектору F3):
Чаще всего с подобным расположением векторов мы встречаемся в задачах, где необходимо обозначить все силы, действующие на тело.
Одним из важных этапов решение «векторной части» этих задач является правильный выбор расположения осей. Он заключается в том, чтобы расположить оси так, чтобы как можно большее число векторов оказались им параллельны.
Как правило, оси располагаются под прямым углом друг к другу, чтобы не получить лишней работы с углами.
Сделаем это для данного рисунка:
Мы видим, что остальные векторы расположены к осям под каким-то углом.
Пунктиром проведем горизонтальную линию и отметим этот угол, а затем отметим другие равные ему углы:
Пришло время искать проекции. У нас две оси, поэтому сделаем для удобства табличку:
Мы располагали оси так, чтобы некоторые векторы были расположены параллельно осям, значит их проекции будут равняться их длинам.
Оси перпендикулярны друг другу, поэтому некоторые проекции будут равняться нулю. Запишем это:
Переходим к векторам, которые расположены под углом.
Выглядит страшно, но это не так!
Дальше идет чистая геометрия. Чтобы не запутаться, рассмотрим лишь часть рисунка. А лучше и вовсе перерисовать его часть, могут открыться много новых вещей.
Из конца вектора F1 проведем перпендикуляр к оси Y. Мы получим прямоугольный треугольник, где нам известен угол (альфа) и гипотенуза (вектор).
Обозначим, что является проекцией. Это катет:
Здесь на помощь придет тригонометрия. Этот катет прилежащий к известному углу. Синус угла есть проекция катета, деленная на гипотенузу. Отсюда можно выразить катет (проекцию) и записать ее в таблицу.
Вспомни, когда мы первый раз встретились с тригонометрией, изучая векторы. Мы тоже рассматривали прямоугольный треугольник.
Найдем проекцию на ось Х. Это, кажется, сложнее, ведь мы не знаем угол…
Знаем! Ведь проекция вектора на ось Х – то же самое, что противолежащий катет уже рассмотренного треугольника, смотри:
Значит, проекцию на ось Х можно найти через косинус.
Не забываем смотреть на направления векторов!
Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.
Значит, проекцию на ось Х можно найти через косинус.
Не забываем смотреть на направления векторов!
Попробуй найти проекции четвертого вектора самостоятельно и сверься с таблицей.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук – ведущий курсов
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж – 19 лет (c 2003 года);
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
- отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.
Содержание:
Скалярные и векторные величины:
В 7-м и 8-м классах мы рассматривали различные физические величины. Для одних величин достаточно знать их числовое значение и единицу измерения. Например, масса
На рисунках 14, а и 14, б девочка действует на санки силой, имеющей одно и то же числовое значение. Но в первом случае санки лишь немного погрузились в снег, а во втором — пришли в движение. Значит, сила определяется не только числовым значением, но и направлением. Сила — величина векторная.
Векторной величиной является и скорость движения тел (рис. 15), и многие другие физические величины.
Что нужно знать о векторных величинах (векторах)
Векторы характеризуются модулем и направлением в пространстве
Модулем вектора называется его числовое значение.
Вектор изображают в виде направленного отрезка (стрелки). Стрелка указывает, куда направлен вектор (рис. 14, 15). Длина стрелки характеризует модуль вектора (рис. 16). Над буквенным обозначением вектора ставят стрелку, например: 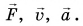
Модуль вектора обозначают той же буквой, но без стрелки над ней или символом 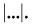
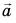
Модуль любого (не равного нулю) вектора — число положительное.
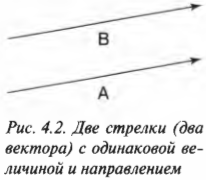
Векторы равны между собой, если равны их модули и одинаковы направления
Равные векторы лежат на одной и той же прямой или на параллельных прямых и направлены в одну и ту же сторону. На рисунке 17 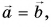
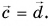
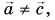
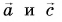
Угол между векторами
Чтобы найти угол 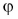
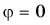
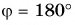
Умножение вектора на число
Произведение вектора 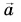
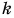
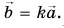
Модуль вектора 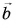
Если 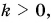
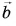
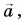
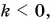
На рисунке 19 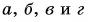
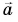
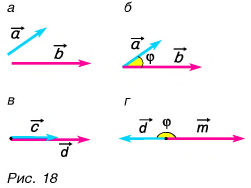
Противоположные векторы
Вектор 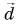
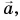
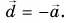
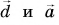
Сложение векторов
В 7-м классе вы складывали силы, направленные или одинаково, или в противоположные стороны. Результатом сложения в первом случае была сила, модуль которой равен 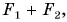
То же самое получается и при сложении векторов 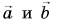
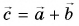
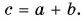
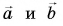
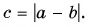
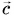
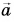
А как сложить векторы, направленные под любым углом друг к другу? Для этого можно использовать любое из двух следующих далее правил.
Правило параллелограмма
Совместим начала векторов 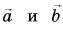
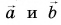
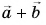
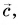
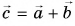
Правило треугольника
Совместим конец вектора 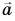
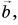
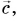
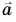
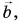
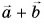
Из рисунков 21, б и 21, в ясно, что правило треугольника и правило параллелограмма дают одинаковые результаты. А как найти разность векторов?
Вычитание векторов
Пусть начала векторов 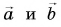
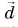
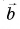
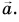
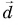
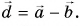
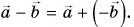
Правило многоугольника
Чтобы найти сумму нескольких векторов (например, 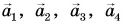
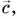
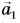
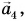
Правило многоугольника следует из правила треугольника.
Модуль суммы векторов
Не путайте модуль суммы векторов, т. е. 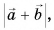
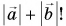
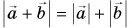
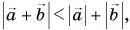
Нуль-вектор
Пусть вектор 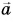
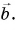
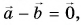
Главные выводы:
- Векторные величины характеризуются модулем и направлением, скалярные — только числовым значением.
- Сумму двух векторов находят по правилу параллелограмма или треугольника.
- Разность двух векторов находят, проводя вектор из конца вычитаемого вектора в конец уменьшаемого (при совмещенных началах векторов).
- Разность векторов
можно найти как сумму
- Произведение вектора
на число
есть вектор
При
направления векторов
совпадают, а при
— противоположны. Модуль вектора
равен
Скалярные и векторные величины
К пониманию того, что для описания природы нужно использовать язык математики, ученые пришли давно. Собственно, некоторые разделы математики и были созданы для того, чтобы описывать природу кратким и доступным языком. Так, для определения мгновенной скорости, работы переменной силы, объема тел неправильной формы и т. д. были созданы дифференциальное и интегральное исчисления. Для более наглядного описания физических процессов научились строить графики функций, а для быстрой обработки результатов эксперимента придумали методы приближенных вычислений. Вспомним скалярные и векторные величины, без которых вам не обойтись при изучении курса физики 10 класса.
Физические величины, используемые в физике для количественной характеристики физических явлений и объектов, делятся на два больших класса: скалярные величины и векторные величины.
К скалярным величинам, или скалярам (от лат. scalaris — ступенчатый), относятся величины, которые определяются только значением. Например, масса тела — скалярная величина, и если мы говорим, что масса тела равна двум килограммам (m=2 кг), то полностью определяем эту величину. Сложить две скалярные физические величины означает сложить их значения, представленные в одинаковых единицах. Понятно, что складывать можно только однородные скаляры (например, нельзя складывать массу и время, плотность и работу и т. д.).
Для определения векторных величин важно знать не только их значения, но и направления. Вектор (от лат. vector — носитель) — это направленный отрезок, то есть отрезок, имеющий и длину, и направление. Длину направленного отрезка называют модулем вектора. Обозначают векторные величины буквами греческого и латинского алфавитов, над которыми ставят стрелки, или полужирными буквами. Например, скорость записывают так: v или 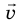
Правила сложения (вычитания) векторов отличаются от правил сложения (вычитания) скалярных величин.
Сумму двух векторов находят по правилу параллелограмма или по правилу треугольника (рис. 3.1, 3.2). Как найти сумму нескольких векторов, показано на рис. 3.3, как найти разность двух векторов, показано на рис. 3.4.
В результате умножения векторной величины 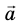
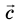
Обратите внимание! Единица произведения векторной и скалярной величин определяется как произведение единицы одной величины на единицу другой. Например, нужно найти перемещение самолета, который в течение 0,5 ч летит на север со скоростью 500 км/ч. Вектор перемещения: 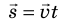
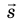
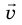
- Заказать решение задач по физике
Как найти проекции вектора на оси координат
Осуществлять математические операции с векторами гораздо сложнее, чем со скалярами, поэтому, решая задачи, от векторных физических величин переходят к их проекциям на оси координат.
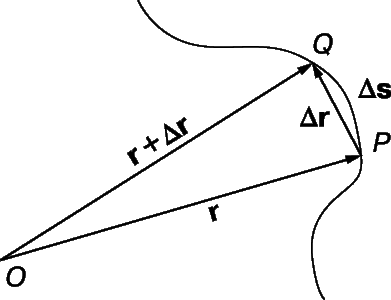
Пусть вектор 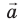
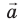
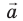
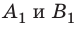
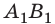
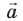
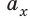
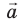
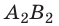
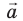
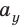
В общем случае проекцию вектора находят обычными геометрическими методами (рис. 3.7, а). На практике часто приходится иметь дело со случаями, когда вектор параллелен или перпендикулярен оси координат.
Если вектор параллелен оси координат, а его направление совпадает с направлением оси, то его проекция на эту ось положительна и равна модулю вектора (рис. 3.7, б). Если направление вектора противоположно направлению оси координат, то его проекция на эту ось равна модулю вектора, взятому с противоположным знаком (рис. 3.7, в). Если же вектор перпендикулярен оси координат, то его проекция на эту ось равна нулю (рис. 3.7, г). Очень важным свойством проекций является то, что проекция суммы двух векторов (рис. 3.8) или нескольких векторов на координатную ось равна алгебраической сумме проекций этих векторов на данную ось.
Именно это свойств позволяет заменять в уравнении векторные величины их проекциями — скалярными величинами и далее решать полученное уравнение обычными алгебраическими методами.
- Проекция вектора на ось
- Путь и перемещение
- Равномерное прямолинейное движение
- Прямолинейное неравномерное движение
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
Векторная величина — физическая величина, являющаяся вектором (тензором ранга 1). Противопоставляется с одной стороны скалярным (тензорам ранга 0), с другой — тензорным величинам (строго говоря — тензорам ранга 2 и более). Также может противопоставляться тем или иным объектам совершенно другой математической природы.
В большинстве случаев термин вектор употребляется в физике для обозначения вектора в так называемом «физическом пространстве», т.е. в обычном трехмерном пространстве в классической физике или в четырехмерном[1] пространстве-времени в современной физике (в последнем случае понятие вектора и векторной величины совпадают с понятием 4-вектора и 4-векторной величины).
Употребление словосочетания «векторная величина» практически исчерпывается этим. Что же касается употребления термина «вектор», то оно, несмотря на тяготение по умолчанию к этому же полю применимости, в большом количестве случаев всё же весьма далеко выходит за такие рамки. Об этом см. ниже.
Содержание
- 1 Употребление терминов вектор и векторная величина в физике
- 2 Генезис векторных величин
- 2.1 Классический трехмерный случай
- 2.2 Современный четырехмерный случай
- 3 Виды векторов применительно к физике
- 4 Примечания
Употребление терминов вектор и векторная величина в физике
В целом в физике понятие вектора практически полностью совпадает с таковым в математике. Однако есть терминологическая специфика, связанная с тем, что в современной математике это понятие несколько излишне абстрактно (по отношению к нуждам физики).
В математике, произнося «вектор» понимают скорее вектор вообще, т.е. любой вектор любого сколь угодно абстрактного линейного пространства любой размерности и природы, что, если не прилагать специальных усилий, может приводить даже к путанице (не столько, конечно, по существу, сколько по удобству словоупотребления). Если же необходимо конкретизировать, в математическом стиле приходится или говорить довольно длинно («вектор такого-то и такого-то пространства»), или иметь в виду подразумеваемое явно описанным контекстом.
В физике же практически всегда речь идет не о математических объектах (обладающих теми или иными формальными свойствами) вообще, а об определенной их конкретной («физической») привязке. Учитывая эти соображения конкретности с соображениями краткости и удобства, можно понять, что терминологическая практика в физике заметно отличается от математической. Однако она не входит с последней в явное противоречие. Этого удается достичь несколькими простыми «приемами». Прежде всего, к ним относится соглашение об употребление термина по умолчанию (когда контекст особо не оговаривается). Так, в физике, в отличие от математики, под словом вектор без дополнительных уточнений обычно понимается не «какой-то вектор любого линейного пространства вообще», а прежде всего вектор, связанный с «обычным физическим пространством» (трехмерным пространством классической физики или четырехмерным пространством-временем[2] физики релятивистской). Для векторов же пространств, не связанных прямо и непосредственно с «физическим пространством» или «пространством-временем», как раз применяют специальные названия (иногда включающие слово «вектор», но с уточнением). Если вектор некоторого пространства, не связанного прямо и непосредственно с «физическим пространством» или «пространством-временем» (и которое трудно сразу как-то определенно охарактеризовать), вводится в теории, он часто специально описывается как «абстрактный вектор».
Всё сказанное еще в большей степени, чем к термину «вектор», относится к термину «векторная величина». Умолчание в этом случае еще жестче подразумевает привязку к «обычному пространству» или пространству-времени, а употребление по отношению к элементам абстрактных векторных пространств скорее практически не встречается, по крайней мере, такое применение видится редчайшим исключением (если вообще не оговоркой).
В физике векторами чаще всего, а векторными величинами — практически всегда — называют векторы двух сходных между собою классов:
- в классической физике (классической механике, электродинамике в классической трехмерной формулировке и в других областях физики, преимущественно сформировавшихся до начала ХХ века) векторными величинами или просто векторами называют, как правило, векторы обычного трехмерного пространства — т.е. обычные «геометрические» векторы или, быть может, отличающиеся от таковых на скалярный множитель (в том числе и на множитель размерный). Хотя в этих областях физики фактически и применялись разнообразные объекты, осознаваемые нынешней математикой как векторы — в физической терминологии это почти не получило отражения (так например, преобразование Фурье в классической электродинамике и классической теории сплошных сред весьма интенсивно применяется, но традиционно почти не рассматривается в контексте классической с использованием слова «вектор» применительно к функциям, хотя с математической точки зрения это было бы вполне законно[3]). Пожалуй, единственным явным исключением из правила является достаточно свободное векторами элементов фазового или конфигурационного пространств[4].
- в релятивистской физике[5] (начиная с Пуанкаре, Планка и Минковского) и, в значительной степени, в современной теоретической физике под векторами и векторными величинами понимаются прежде всего векторы четырехмерного пространства-времени[6] и непосредственно с ним связанные (отличающиеся на скалярный множитель от векторов 4-перемещения) — 4-векторы.
- в квантовой механике, квантовой теории поля итд слово «вектор» стало стандартно применяться и для обозначения такого объекта, как вектор состояния. Этот вектор может иметь в принципе любую размерность, а как правило — бесконечномерен. Однако путаницы тут практически не возникает, поскольку слово вектор тут используется практически исключительно в устойчивом сочетании вектор состояния, и никогда отдельно, за исключением разве что случаев, когда контекст уже настолько очевиден, что путаница просто невозможна (например, при повторном употреблении отдельного слова вектор в отношении объекта, который только что перед этим был назван, как вектор состояния или при использовании однозначных специфических обозначений — таких например, как скобки Дирака, — или соответствующих им терминов. Для ряда векторов специфических пространств используются специальные слова (такие, как например спиноры) или явные названия (вектор цветового пространства, изотопический спин итд). Притом что словосочетание «векторная величина» практически никогда не применяется к таким абстрактным векторам. Всё это позволило термину «векторный» сохранить в качестве, пожалуй, основного смысла — смысл 4-вектора. Именно этот смысл вкладывается в термины векторное поле, векторная частица (векторный бозон, векторный мезон); сопряженный смысл в подобных терминах имеет и слово скалярный.
Примеры векторных физических величин: скорость, сила, поток тепла.
Генезис векторных величин
Каким образом физические «векторные величины» привязаны к пространству? Прежде всего, бросается в глаза то, что размерность векторных величин (в том обычном смысле употребления этого термина, который разъяснен выше) совпадает с размерностью одного и того же «физического» (и «геометрического») пространатсва, например, пространство трехмерно и вектор электрического поля трехмерен. Интуитивно можно заметить также, что любая векторная физическая величина, какую бы туманную связь она не имела с обычной пространственной протяженностью, тем не менее имеет вполне определенное направление именно в этом обычном пространстве.
Однако оказывается, что можно достичь и гораздо большего, прямо «сведя» весь набор векторных величин физики к простейшим «геометрическим» векторам, вернее даже — к одному вектору — вектору элементарного перемещения, а более правильно было бы сказать — произведя их всех от него.
Эта процедура имеет две различные (хотя по сути детально повторяющие друг друга) реализации для трехмерного случая классической физики и для четырехмерной пространственно-временной формулировки, обычной для современной физики.
Классический трехмерный случай
Будем исходить из обычного трехмерного «геометрического» пространства, в котором мы живем и можем перемещаться.
В качестве исходного и образцового вектора возьмем вектор бесконечно малого перемещения. Довольно очевидно, что это обычный «геометрический» вектор (как и вектор конечного перемещения).
Заметим теперь сразу, что умножение вектора на скаляр всегда дает новый вектор. То же можно сказать о сумме и разности векторов. В этой главе мы не будем делать разницы между полярными и аксиальными векторами[7], поэтому заметим, что и векторное произведение двух векторов дает новый вектор.
Также новый вектор дает дифференцирование вектора по скаляру (поскольку такая производная есть предел отношения разности векторов к скаляру). Это можно сказать дальше и о производных всех высших порядков. То же верно по отношению к интегрированию по скалярам (времени, объему).
Теперь заметим, что, исходя из радиус-вектора r или из элементарного перемещения dr, мы легко понимаем, что векторами являются (поскольку время — скаляр) такие кинематические величины, как
Из скорости и ускорения, умножением на скаляр (массу), появляются
- импульс,
- сила.
Поскольку нас сейчас интересуют и псевдовекторы, заметим, что
- угловая скорость,
- момент импульса — появляются совершенно понятным образом.[8]
- с помощью формулы силы Лоренца напряженность электрического поля и вектор магнитной индукции привязаны к векторам силы и скорости.
Продолжая эту процедуру, мы обнаруживаем, что все известные нам векторные величины оказываются теперь не только интуитивно, но и формально, привязаны к исходному пространству. А именно все они в некотором смысле являются его элементами, т.к. выражаются в сущности как линейные комбинации других векторов (со скалярными множителями, возможно, и размерными, но скалярными, а поэтому формально вполне законными).
Современный четырехмерный случай
Ту же процедуру можно проделать исходя из четырехмерного перемещения. Оказывается, что все 4-векторные величины «происходят» от 4-перемещения, являясь поэтому в некотором смысле такими же векторами пространства-времени, как и само 4-перемещение.
Виды векторов применительно к физике
- Полярный или истинный вектор — обычный вектор.
- Аксиальный вектор (псевдовектор) — на самом деле не является настоящим вектором, однако формально почти не отличается от последнего, за исключением того, что меняет направление на противоположное при изменении ориентации системы координат (например, при зеркальном отражении системы координат). Примеры псевдовекторов: все величины, определяемые через векторное произведение двух полярных векторов.
- Для сил выделяется несколько различных классов эквивалентности.
Примечания
- ↑ Во многих современных теориях размерность фундаментального пространства-времени больше, чем 4; впрочем, это в принципе довольно мало что меняет, к тому же ни одна из этих теорий пока не достигла статуса общепризнанной и достаточно подтвержденной.
- ↑ Во многих современных теориях, например, в теории струн, пространство-время не 4-мерно, а имеет большее количество измерений, однако является чаще всего достаточно прямым и простым обобщением своего 4-мерного прототипа, а возможность путаницы практически исключена контекстом самих этих теорий (не говоря уже о том, что размерность тогда часто указывается явно, а других, кроме размерности, отличий от обычного пространства-времени не предполагается).
- ↑ Для того, чтобы избежать противоречий между физической и математической терминологией, существует такой способ: вместо выражения «вектор такого-то пространства» применять синонимичное выражение «элемент такого-то пространства», математически полностью эквивалентное, но не создающее путаницы при употреблении наряду с обычных для физики терминологических традиций.
- ↑ трудно сказать, что послужило этому в большей степени: то, что эти пространства (особенно конфигурационное) выглядят слишком прямым обобщением обычного физического пространства, в частных случаях просто с последним совпадающим, или то, что теоретическая механика, в которой эти понятия возникли, считается разделом не физики, а математики.
- ↑ Под релятивистской физикой тут прежде всего понимается стандартная 4-мерная формулировка релятивистской механики, электродинамики и других теорий. В принуипе, такая формулировка используется и для квантовых теорий, и для не-квантовых.
- ↑ Наиболее явным выходом за эти рамки по умолчанию (т.е. без специальных терминологических уточняющих маркеров) являются уже упоминавшиеся теории, основанные на предположении о большей, чем 4, размерности фундаментального физического пространства-времени, начиная с теории Калуцы, до теории струн итд.
- ↑ При нужде такое разделение легко произвести, но нас сейчас интересует в первую построение наиболее полного набора векторных физических величин, а не их классификация, на этом мы и сосредоточимся.
- ↑ Для угловой скорости, правда, проще всего применить обратное рассуждение: поскольку векторное произведение угловой скорости и радиус-вектора есть скорость, значит угловая скорость — вектор (точнее — псевдовектор).
This article is about the vectors mainly used in physics and engineering to represent directed quantities. For mathematical vectors in general, see Vector (mathematics and physics). For other uses, see Vector (disambiguation).
A vector pointing from A to B
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector[1] or spatial vector[2]) is a geometric object that has magnitude (or length) and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a directed line segment, or graphically as an arrow connecting an initial point A with a terminal point B,[3] and denoted by 
A vector is what is needed to «carry» the point A to the point B; the Latin word vector means «carrier».[4] It was first used by 18th century astronomers investigating planetary revolution around the Sun.[5] The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from A to B. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors,[6] operations which obey the familiar algebraic laws of commutativity, associativity, and distributivity. These operations and associated laws qualify Euclidean vectors as an example of the more generalized concept of vectors defined simply as elements of a vector space.
Vectors play an important role in physics: the velocity and acceleration of a moving object and the forces acting on it can all be described with vectors.[7] Many other physical quantities can be usefully thought of as vectors. Although most of them do not represent distances (except, for example, position or displacement), their magnitude and direction can still be represented by the length and direction of an arrow. The mathematical representation of a physical vector depends on the coordinate system used to describe it. Other vector-like objects that describe physical quantities and transform in a similar way under changes of the coordinate system include pseudovectors and tensors.[8]
History[edit]
The vector concept, as we know it today, is the result of a gradual development over a period of more than 200 years. About a dozen people contributed significantly to its development.[9] In 1835, Giusto Bellavitis abstracted the basic idea when he established the concept of equipollence. Working in a Euclidean plane, he made equipollent any pair of parallel line segments of the same length and orientation. Essentially, he realized an equivalence relation on the pairs of points (bipoints) in the plane, and thus erected the first space of vectors in the plane.[9]: 52–4 The term vector was introduced by William Rowan Hamilton as part of a quaternion, which is a sum q = s + v of a Real number s (also called scalar) and a 3-dimensional vector. Like Bellavitis, Hamilton viewed vectors as representative of classes of equipollent directed segments. As complex numbers use an imaginary unit to complement the real line, Hamilton considered the vector v to be the imaginary part of a quaternion:[10]
The algebraically imaginary part, being geometrically constructed by a straight line, or radius vector, which has, in general, for each determined quaternion, a determined length and determined direction in space, may be called the vector part, or simply the vector of the quaternion.
Several other mathematicians developed vector-like systems in the middle of the nineteenth century, including Augustin Cauchy, Hermann Grassmann, August Möbius, Comte de Saint-Venant, and Matthew O’Brien. Grassmann’s 1840 work Theorie der Ebbe und Flut (Theory of the Ebb and Flow) was the first system of spatial analysis that is similar to today’s system, and had ideas corresponding to the cross product, scalar product and vector differentiation. Grassmann’s work was largely neglected until the 1870s.[9] Peter Guthrie Tait carried the quaternion standard after Hamilton. His 1867 Elementary Treatise of Quaternions included extensive treatment of the nabla or del operator ∇. In 1878, Elements of Dynamic was published by William Kingdon Clifford. Clifford simplified the quaternion study by isolating the dot product and cross product of two vectors from the complete quaternion product. This approach made vector calculations available to engineers—and others working in three dimensions and skeptical of the fourth.
Josiah Willard Gibbs, who was exposed to quaternions through James Clerk Maxwell’s Treatise on Electricity and Magnetism, separated off their vector part for independent treatment. The first half of Gibbs’s Elements of Vector Analysis, published in 1881, presents what is essentially the modern system of vector analysis.[9][6] In 1901, Edwin Bidwell Wilson published Vector Analysis, adapted from Gibb’s lectures, which banished any mention of quaternions in the development of vector calculus.
Overview[edit]
In physics and engineering, a vector is typically regarded as a geometric entity characterized by a magnitude and a direction. It is formally defined as a directed line segment, or arrow, in a Euclidean space.[11] In pure mathematics, a vector is defined more generally as any element of a vector space. In this context, vectors are abstract entities which may or may not be characterized by a magnitude and a direction. This generalized definition implies that the above-mentioned geometric entities are a special kind of vectors, as they are elements of a special kind of vector space called Euclidean space. This particular article is about vectors strictly defined as arrows in Euclidean space. When it becomes necessary to distinguish these special vectors from vectors as defined in pure mathematics, they are sometimes referred to as geometric, spatial, or Euclidean vectors.
Being an arrow, a Euclidean vector possesses a definite initial point and terminal point. A vector with fixed initial and terminal point is called a bound vector.[12] When only the magnitude and direction of the vector matter, then the particular initial point is of no importance, and the vector is called a free vector. Thus two arrows 

Further information[edit]
In classical Euclidean geometry (i.e., synthetic geometry), vectors were introduced (during the 19th century) as equivalence classes under equipollence, of ordered pairs of points; two pairs (A, B) and (C, D) being equipollent if the points A, B, D, C, in this order, form a parallelogram. Such an equivalence class is called a vector, more precisely, a Euclidean vector.[13] The equivalence class of (A, B) is often denoted 
A Euclidean vector is thus an equivalence class of directed segments with the same magnitude (e.g., the length of the line segment (A, B)) and same direction (e.g., the direction from A to B).[14] In physics, Euclidean vectors are used to represent physical quantities that have both magnitude and direction, but are not located at a specific place, in contrast to scalars, which have no direction.[7] For example, velocity, forces and acceleration are represented by vectors.
In modern geometry, Euclidean spaces are often defined from linear algebra. More precisely, a Euclidean space E is defined as a set to which is associated an inner product space of finite dimension over the reals 


Sometimes, Euclidean vectors are considered without reference to a Euclidean space. In this case, a Euclidean vector is an element of a normed vector space of finite dimension over the reals, or, typically, an element of 

The Euclidean space 



Examples in one dimension[edit]
Since the physicist’s concept of force has a direction and a magnitude, it may be seen as a vector. As an example, consider a rightward force F of 15 newtons. If the positive axis is also directed rightward, then F is represented by the vector 15 N, and if positive points leftward, then the vector for F is −15 N. In either case, the magnitude of the vector is 15 N. Likewise, the vector representation of a displacement Δs of 4 meters would be 4 m or −4 m, depending on its direction, and its magnitude would be 4 m regardless.
In physics and engineering[edit]
Vectors are fundamental in the physical sciences. They can be used to represent any quantity that has magnitude, has direction, and which adheres to the rules of vector addition. An example is velocity, the magnitude of which is speed. For instance, the velocity 5 meters per second upward could be represented by the vector (0, 5) (in 2 dimensions with the positive y-axis as ‘up’). Another quantity represented by a vector is force, since it has a magnitude and direction and follows the rules of vector addition.[7] Vectors also describe many other physical quantities, such as linear displacement, displacement, linear acceleration, angular acceleration, linear momentum, and angular momentum. Other physical vectors, such as the electric and magnetic field, are represented as a system of vectors at each point of a physical space; that is, a vector field. Examples of quantities that have magnitude and direction, but fail to follow the rules of vector addition, are angular displacement and electric current. Consequently, these are not vectors.
In Cartesian space[edit]
In the Cartesian coordinate system, a bound vector can be represented by identifying the coordinates of its initial and terminal point. For instance, the points A = (1, 0, 0) and B = (0, 1, 0) in space determine the bound vector 
In Cartesian coordinates, a free vector may be thought of in terms of a corresponding bound vector, in this sense, whose initial point has the coordinates of the origin O = (0, 0, 0). It is then determined by the coordinates of that bound vector’s terminal point. Thus the free vector represented by (1, 0, 0) is a vector of unit length—pointing along the direction of the positive x-axis.
This coordinate representation of free vectors allows their algebraic features to be expressed in a convenient numerical fashion. For example, the sum of the two (free) vectors (1, 2, 3) and (−2, 0, 4) is the (free) vector
Euclidean and affine vectors[edit]
In the geometrical and physical settings, it is sometimes possible to associate, in a natural way, a length or magnitude and a direction to vectors. In addition, the notion of direction is strictly associated with the notion of an angle between two vectors. If the dot product of two vectors is defined—a scalar-valued product of two vectors—then it is also possible to define a length; the dot product gives a convenient algebraic characterization of both angle (a function of the dot product between any two non-zero vectors) and length (the square root of the dot product of a vector by itself). In three dimensions, it is further possible to define the cross product, which supplies an algebraic characterization of the area and orientation in space of the parallelogram defined by two vectors (used as sides of the parallelogram). In any dimension (and, in particular, higher dimensions), it’s possible to define the exterior product, which (among other things) supplies an algebraic characterization of the area and orientation in space of the n-dimensional parallelotope defined by n vectors.
In a pseudo-Euclidean space, a vector’s squared length can be positive, negative, or zero. An important example is Minkowski space (which is important to our understanding of special relativity).
However, it is not always possible or desirable to define the length of a vector. This more general type of spatial vector is the subject of vector spaces (for free vectors) and affine spaces (for bound vectors, as each represented by an ordered pair of «points»). One physical example comes from thermodynamics, where many quantities of interest can be considered vectors in a space with no notion of length or angle.[15]
Generalizations[edit]
In physics, as well as mathematics, a vector is often identified with a tuple of components, or list of numbers, that act as scalar coefficients for a set of basis vectors. When the basis is transformed, for example by rotation or stretching, then the components of any vector in terms of that basis also transform in an opposite sense. The vector itself has not changed, but the basis has, so the components of the vector must change to compensate. The vector is called covariant or contravariant, depending on how the transformation of the vector’s components is related to the transformation of the basis. In general, contravariant vectors are «regular vectors» with units of distance (such as a displacement), or distance times some other unit (such as velocity or acceleration); covariant vectors, on the other hand, have units of one-over-distance such as gradient. If you change units (a special case of a change of basis) from meters to millimeters, a scale factor of 1/1000, a displacement of 1 m becomes 1000 mm—a contravariant change in numerical value. In contrast, a gradient of 1 K/m becomes 0.001 K/mm—a covariant change in value (for more, see covariance and contravariance of vectors). Tensors are another type of quantity that behave in this way; a vector is one type of tensor.
In pure mathematics, a vector is any element of a vector space over some field and is often represented as a coordinate vector. The vectors described in this article are a very special case of this general definition, because they are contravariant with respect to the ambient space. Contravariance captures the physical intuition behind the idea that a vector has «magnitude and direction».
Representations[edit]
Vectors are usually denoted in lowercase boldface, as in 






Vectors are usually shown in graphs or other diagrams as arrows (directed line segments), as illustrated in the figure. Here, the point A is called the origin, tail, base, or initial point, and the point B is called the head, tip, endpoint, terminal point or final point. The length of the arrow is proportional to the vector’s magnitude, while the direction in which the arrow points indicates the vector’s direction.
On a two-dimensional diagram, a vector perpendicular to the plane of the diagram is sometimes desired. These vectors are commonly shown as small circles. A circle with a dot at its centre (Unicode U+2299 ⊙) indicates a vector pointing out of the front of the diagram, toward the viewer. A circle with a cross inscribed in it (Unicode U+2297 ⊗) indicates a vector pointing into and behind the diagram. These can be thought of as viewing the tip of an arrow head on and viewing the flights of an arrow from the back.
A vector in the Cartesian plane, showing the position of a point A with coordinates (2, 3).
In order to calculate with vectors, the graphical representation may be too cumbersome. Vectors in an n-dimensional Euclidean space can be represented as coordinate vectors in a Cartesian coordinate system. The endpoint of a vector can be identified with an ordered list of n real numbers (n-tuple). These numbers are the coordinates of the endpoint of the vector, with respect to a given Cartesian coordinate system, and are typically called the scalar components (or scalar projections) of the vector on the axes of the coordinate system.
As an example in two dimensions (see figure), the vector from the origin O = (0, 0) to the point A = (2, 3) is simply written as
The notion that the tail of the vector coincides with the origin is implicit and easily understood. Thus, the more explicit notation 
In three dimensional Euclidean space (or R3), vectors are identified with triples of scalar components:
also written,
This can be generalised to n-dimensional Euclidean space (or Rn).
These numbers are often arranged into a column vector or row vector, particularly when dealing with matrices, as follows:
Another way to represent a vector in n-dimensions is to introduce the standard basis vectors. For instance, in three dimensions, there are three of them:
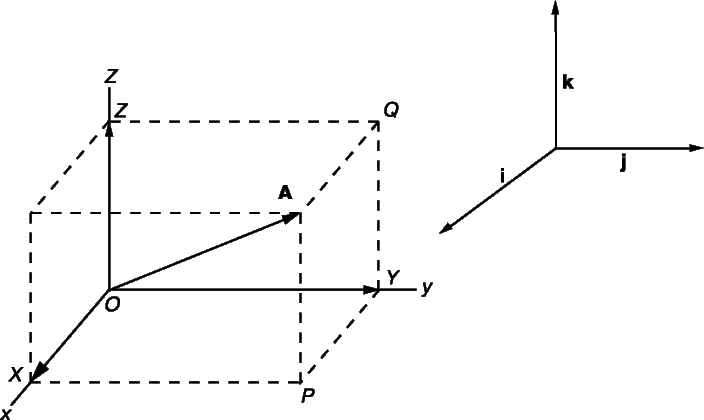
These have the intuitive interpretation as vectors of unit length pointing up the x-, y-, and z-axis of a Cartesian coordinate system, respectively. In terms of these, any vector a in R3 can be expressed in the form:
or
where a1, a2, a3 are called the vector components (or vector projections) of a on the basis vectors or, equivalently, on the corresponding Cartesian axes x, y, and z (see figure), while a1, a2, a3 are the respective scalar components (or scalar projections).
In introductory physics textbooks, the standard basis vectors are often denoted 

The notation ei is compatible with the index notation and the summation convention commonly used in higher level mathematics, physics, and engineering.
Decomposition or resolution[edit]
As explained above, a vector is often described by a set of vector components that add up to form the given vector. Typically, these components are the projections of the vector on a set of mutually perpendicular reference axes (basis vectors). The vector is said to be decomposed or resolved with respect to that set.
Illustration of tangential and normal components of a vector to a surface.
The decomposition or resolution[16] of a vector into components is not unique, because it depends on the choice of the axes on which the vector is projected.
Moreover, the use of Cartesian unit vectors such as 


The choice of a basis does not affect the properties of a vector or its behaviour under transformations.
A vector can also be broken up with respect to «non-fixed» basis vectors that change their orientation as a function of time or space. For example, a vector in three-dimensional space can be decomposed with respect to two axes, respectively normal, and tangent to a surface (see figure). Moreover, the radial and tangential components of a vector relate to the radius of rotation of an object. The former is parallel to the radius and the latter is orthogonal to it.[17]
In these cases, each of the components may be in turn decomposed with respect to a fixed coordinate system or basis set (e.g., a global coordinate system, or inertial reference frame).
Basic properties[edit]
The following section uses the Cartesian coordinate system with basis vectors
and assumes that all vectors have the origin as a common base point. A vector a will be written as
Equality[edit]
Two vectors are said to be equal if they have the same magnitude and direction. Equivalently they will be equal if their coordinates are equal. So two vectors
and
are equal if
Opposite, parallel, and antiparallel vectors[edit]
Two vectors are opposite if they have the same magnitude but opposite direction. So two vectors
and
are opposite if
Two vectors are parallel if they have the same direction but not necessarily the same magnitude, or antiparallel if they have opposite direction but not necessarily the same magnitude.
Addition and subtraction[edit]
The sum of a and b of two vectors may be defined as
The resulting vector is sometimes called the resultant vector of a and b.
The addition may be represented graphically by placing the tail of the arrow b at the head of the arrow a, and then drawing an arrow from the tail of a to the head of b. The new arrow drawn represents the vector a + b, as illustrated below:[7]
This addition method is sometimes called the parallelogram rule because a and b form the sides of a parallelogram and a + b is one of the diagonals. If a and b are bound vectors that have the same base point, this point will also be the base point of a + b. One can check geometrically that a + b = b + a and (a + b) + c = a + (b + c).
The difference of a and b is
Subtraction of two vectors can be geometrically illustrated as follows: to subtract b from a, place the tails of a and b at the same point, and then draw an arrow from the head of b to the head of a. This new arrow represents the vector (-b) + a, with (-b) being the opposite of b, see drawing. And (-b) + a = a − b.
Scalar multiplication[edit]
Scalar multiplication of a vector by a factor of 3 stretches the vector out.
A vector may also be multiplied, or re-scaled, by a real number r. In the context of conventional vector algebra, these real numbers are often called scalars (from scale) to distinguish them from vectors. The operation of multiplying a vector by a scalar is called scalar multiplication. The resulting vector is
Intuitively, multiplying by a scalar r stretches a vector out by a factor of r. Geometrically, this can be visualized (at least in the case when r is an integer) as placing r copies of the vector in a line where the endpoint of one vector is the initial point of the next vector.
If r is negative, then the vector changes direction: it flips around by an angle of 180°. Two examples (r = −1 and r = 2) are given below:
The scalar multiplications −a and 2a of a vector a
Scalar multiplication is distributive over vector addition in the following sense: r(a + b) = ra + rb for all vectors a and b and all scalars r. One can also show that a − b = a + (−1)b.
Length[edit]
The length or magnitude or norm of the vector a is denoted by ‖a‖ or, less commonly, |a|, which is not to be confused with the absolute value (a scalar «norm»).
The length of the vector a can be computed with the Euclidean norm,
which is a consequence of the Pythagorean theorem since the basis vectors e1, e2, e3 are orthogonal unit vectors.
This happens to be equal to the square root of the dot product, discussed below, of the vector with itself:
Unit vector[edit]
The normalization of a vector a into a unit vector â
A unit vector is any vector with a length of one; normally unit vectors are used simply to indicate direction. A vector of arbitrary length can be divided by its length to create a unit vector.[14] This is known as normalizing a vector. A unit vector is often indicated with a hat as in â.
To normalize a vector a = (a1, a2, a3), scale the vector by the reciprocal of its length ‖a‖. That is:
Zero vector[edit]
The zero vector is the vector with length zero. Written out in coordinates, the vector is (0, 0, 0), and it is commonly denoted 
Dot product[edit]
The dot product of two vectors a and b (sometimes called the inner product, or, since its result is a scalar, the scalar product) is denoted by a ∙ b, and is defined as:
where θ is the measure of the angle between a and b (see trigonometric function for an explanation of cosine). Geometrically, this means that a and b are drawn with a common start point, and then the length of a is multiplied with the length of the component of b that points in the same direction as a.
The dot product can also be defined as the sum of the products of the components of each vector as
Cross product[edit]
The cross product (also called the vector product or outer product) is only meaningful in three or seven dimensions. The cross product differs from the dot product primarily in that the result of the cross product of two vectors is a vector. The cross product, denoted a × b, is a vector perpendicular to both a and b and is defined as
where θ is the measure of the angle between a and b, and n is a unit vector perpendicular to both a and b which completes a right-handed system. The right-handedness constraint is necessary because there exist two unit vectors that are perpendicular to both a and b, namely, n and (−n).
An illustration of the cross product
The cross product a × b is defined so that a, b, and a × b also becomes a right-handed system (although a and b are not necessarily orthogonal). This is the right-hand rule.
The length of a × b can be interpreted as the area of the parallelogram having a and b as sides.
The cross product can be written as
For arbitrary choices of spatial orientation (that is, allowing for left-handed as well as right-handed coordinate systems) the cross product of two vectors is a pseudovector instead of a vector (see below).
Scalar triple product[edit]
The scalar triple product (also called the box product or mixed triple product) is not really a new operator, but a way of applying the other two multiplication operators to three vectors. The scalar triple product is sometimes denoted by (a b c) and defined as:
It has three primary uses. First, the absolute value of the box product is the volume of the parallelepiped which has edges that are defined by the three vectors. Second, the scalar triple product is zero if and only if the three vectors are linearly dependent, which can be easily proved by considering that in order for the three vectors to not make a volume, they must all lie in the same plane. Third, the box product is positive if and only if the three vectors a, b and c are right-handed.
In components (with respect to a right-handed orthonormal basis), if the three vectors are thought of as rows (or columns, but in the same order), the scalar triple product is simply the determinant of the 3-by-3 matrix having the three vectors as rows
The scalar triple product is linear in all three entries and anti-symmetric in the following sense:
Conversion between multiple Cartesian bases[edit]
All examples thus far have dealt with vectors expressed in terms of the same basis, namely, the e basis {e1, e2, e3}. However, a vector can be expressed in terms of any number of different bases that are not necessarily aligned with each other, and still remain the same vector. In the e basis, a vector a is expressed, by definition, as
The scalar components in the e basis are, by definition,
In another orthonormal basis n = {n1, n2, n3} that is not necessarily aligned with e, the vector a is expressed as
and the scalar components in the n basis are, by definition,
The values of p, q, r, and u, v, w relate to the unit vectors in such a way that the resulting vector sum is exactly the same physical vector a in both cases. It is common to encounter vectors known in terms of different bases (for example, one basis fixed to the Earth and a second basis fixed to a moving vehicle). In such a case it is necessary to develop a method to convert between bases so the basic vector operations such as addition and subtraction can be performed. One way to express u, v, w in terms of p, q, r is to use column matrices along with a direction cosine matrix containing the information that relates the two bases. Such an expression can be formed by substitution of the above equations to form
Distributing the dot-multiplication gives
Replacing each dot product with a unique scalar gives
and these equations can be expressed as the single matrix equation
This matrix equation relates the scalar components of a in the n basis (u,v, and w) with those in the e basis (p, q, and r). Each matrix element cjk is the direction cosine relating nj to ek.[18] The term direction cosine refers to the cosine of the angle between two unit vectors, which is also equal to their dot product.[18] Therefore,
By referring collectively to e1, e2, e3 as the e basis and to n1, n2, n3 as the n basis, the matrix containing all the cjk is known as the «transformation matrix from e to n«, or the «rotation matrix from e to n» (because it can be imagined as the «rotation» of a vector from one basis to another), or the «direction cosine matrix from e to n«[18] (because it contains direction cosines). The properties of a rotation matrix are such that its inverse is equal to its transpose. This means that the «rotation matrix from e to n» is the transpose of «rotation matrix from n to e«.
The properties of a direction cosine matrix, C are:[19]
- the determinant is unity, |C| = 1;
- the inverse is equal to the transpose;
- the rows and columns are orthogonal unit vectors, therefore their dot products are zero.
The advantage of this method is that a direction cosine matrix can usually be obtained independently by using Euler angles or a quaternion to relate the two vector bases, so the basis conversions can be performed directly, without having to work out all the dot products described above.
By applying several matrix multiplications in succession, any vector can be expressed in any basis so long as the set of direction cosines is known relating the successive bases.[18]
Other dimensions[edit]
With the exception of the cross and triple products, the above formulae generalise to two dimensions and higher dimensions. For example, addition generalises to two dimensions as
and in four dimensions as
The cross product does not readily generalise to other dimensions, though the closely related exterior product does, whose result is a bivector. In two dimensions this is simply a pseudoscalar
A seven-dimensional cross product is similar to the cross product in that its result is a vector orthogonal to the two arguments; there is however no natural way of selecting one of the possible such products.
Physics[edit]
Vectors have many uses in physics and other sciences.
Length and units[edit]
In abstract vector spaces, the length of the arrow depends on a dimensionless scale. If it represents, for example, a force, the «scale» is of physical dimension length/force. Thus there is typically consistency in scale among quantities of the same dimension, but otherwise scale ratios may vary; for example, if «1 newton» and «5 m» are both represented with an arrow of 2 cm, the scales are 1 m:50 N and 1:250 respectively. Equal length of vectors of different dimension has no particular significance unless there is some proportionality constant inherent in the system that the diagram represents. Also length of a unit vector (of dimension length, not length/force, etc.) has no coordinate-system-invariant significance.
Vector-valued functions[edit]
Often in areas of physics and mathematics, a vector evolves in time, meaning that it depends on a time parameter t. For instance, if r represents the position vector of a particle, then r(t) gives a parametric representation of the trajectory of the particle. Vector-valued functions can be differentiated and integrated by differentiating or integrating the components of the vector, and many of the familiar rules from calculus continue to hold for the derivative and integral of vector-valued functions.
Position, velocity and acceleration[edit]
The position of a point x = (x1, x2, x3) in three-dimensional space can be represented as a position vector whose base point is the origin
The position vector has dimensions of length.
Given two points x = (x1, x2, x3), y = (y1, y2, y3) their displacement is a vector
which specifies the position of y relative to x. The length of this vector gives the straight-line distance from x to y. Displacement has the dimensions of length.
The velocity v of a point or particle is a vector, its length gives the speed. For constant velocity the position at time t will be
where x0 is the position at time t = 0. Velocity is the time derivative of position. Its dimensions are length/time.
Acceleration a of a point is vector which is the time derivative of velocity. Its dimensions are length/time2.
Force, energy, work[edit]
Force is a vector with dimensions of mass×length/time2 and Newton’s second law is the scalar multiplication
Work is the dot product of force and displacement
Vectors, pseudovectors, and transformations[edit]
An alternative characterization of Euclidean vectors, especially in physics, describes them as lists of quantities which behave in a certain way under a coordinate transformation. A contravariant vector is required to have components that «transform opposite to the basis» under changes of basis. The vector itself does not change when the basis is transformed; instead, the components of the vector make a change that cancels the change in the basis. In other words, if the reference axes (and the basis derived from it) were rotated in one direction, the component representation of the vector would rotate in the opposite way to generate the same final vector. Similarly, if the reference axes were stretched in one direction, the components of the vector would reduce in an exactly compensating way. Mathematically, if the basis undergoes a transformation described by an invertible matrix M, so that a coordinate vector x is transformed to x′ = Mx, then a contravariant vector v must be similarly transformed via v′ = M
In the language of differential geometry, the requirement that the components of a vector transform according to the same matrix of the coordinate transition is equivalent to defining a contravariant vector to be a tensor of contravariant rank one. Alternatively, a contravariant vector is defined to be a tangent vector, and the rules for transforming a contravariant vector follow from the chain rule.
Some vectors transform like contravariant vectors, except that when they are reflected through a mirror, they flip and gain a minus sign. A transformation that switches right-handedness to left-handedness and vice versa like a mirror does is said to change the orientation of space. A vector which gains a minus sign when the orientation of space changes is called a pseudovector or an axial vector. Ordinary vectors are sometimes called true vectors or polar vectors to distinguish them from pseudovectors. Pseudovectors occur most frequently as the cross product of two ordinary vectors.
One example of a pseudovector is angular velocity. Driving in a car, and looking forward, each of the wheels has an angular velocity vector pointing to the left. If the world is reflected in a mirror which switches the left and right side of the car, the reflection of this angular velocity vector points to the right, but the actual angular velocity vector of the wheel still points to the left, corresponding to the minus sign. Other examples of pseudovectors include magnetic field, torque, or more generally any cross product of two (true) vectors.
This distinction between vectors and pseudovectors is often ignored, but it becomes important in studying symmetry properties. See parity (physics).
See also[edit]
- Affine space, which distinguishes between vectors and points
- Array (data structure)
- Banach space
- Clifford algebra
- Complex number
- Coordinate system
- Covariance and contravariance of vectors
- Four-vector, a non-Euclidean vector in Minkowski space (i.e. four-dimensional spacetime), important in relativity
- Function space
- Grassmann’s Ausdehnungslehre
- Hilbert space
- Normal vector
- Null vector
- Position (geometry)
- Pseudovector
- Quaternion
- Tangential and normal components (of a vector)
- Tensor
- Unit vector
- Vector bundle
- Vector calculus
- Vector notation
- Vector-valued function
Notes[edit]
- ^ Ivanov 2001
- ^ Heinbockel 2001
- ^ Itô 1993, p. 1678; Pedoe 1988
- ^ Latin: vectus, perfect participle of vehere, «to carry»/ veho = «I carry». For historical development of the word vector, see «vector n.«. Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.) and Jeff Miller. «Earliest Known Uses of Some of the Words of Mathematics». Retrieved 2007-05-25.
- ^ The Oxford English Dictionary (2nd. ed.). London: Clarendon Press. 2001. ISBN 9780195219425.
- ^ a b «vector | Definition & Facts». Encyclopedia Britannica. Retrieved 2020-08-19.
- ^ a b c d «Vectors». www.mathsisfun.com. Retrieved 2020-08-19.
- ^ Weisstein, Eric W. «Vector». mathworld.wolfram.com. Retrieved 2020-08-19.
- ^ a b c d Michael J. Crowe, A History of Vector Analysis; see also his «lecture notes» (PDF). Archived from the original (PDF) on January 26, 2004. Retrieved 2010-09-04. on the subject.
- ^ W. R. Hamilton (1846) London, Edinburgh & Dublin Philosophical Magazine 3rd series 29 27
- ^ Itô 1993, p. 1678
- ^ Formerly known as located vector. See Lang 1986, p. 9.
- ^ In some old texts, the pair (A, B) is called a bound vector, and its equivalence class is called a free vector.
- ^ a b «1.1: Vectors». Mathematics LibreTexts. 2013-11-07. Retrieved 2020-08-19.
- ^ Thermodynamics and Differential Forms
- ^ Gibbs, J.W. (1901). Vector Analysis: A Text-book for the Use of Students of Mathematics and Physics, Founded upon the Lectures of J. Willard Gibbs, by E.B. Wilson, Chares Scribner’s Sons, New York, p. 15: «Any vector r coplanar with two non-collinear vectors a and b may be resolved into two components parallel to a and b respectively. This resolution may be accomplished by constructing the parallelogram …»
- ^ «U. Guelph Physics Dept., «Torque and Angular Acceleration»«. Archived from the original on 2007-01-22. Retrieved 2007-01-05.
- ^ a b c d Kane & Levinson 1996, pp. 20–22
- ^ M., Rogers, Robert (2007). Applied mathematics in integrated navigation systems (3rd ed.). Reston, Va.: American Institute of Aeronautics and Astronautics. ISBN 9781563479274. OCLC 652389481.
References[edit]
Mathematical treatments[edit]
- Apostol, Tom (1967). Calculus. Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra. Wiley. ISBN 978-0-471-00005-1.
- Apostol, Tom (1969). Calculus. Vol. 2: Multi-Variable Calculus and Linear Algebra with Applications. Wiley. ISBN 978-0-471-00007-5.
- Heinbockel, J. H. (2001), Introduction to Tensor Calculus and Continuum Mechanics, Trafford Publishing, ISBN 1-55369-133-4.
- Itô, Kiyosi (1993), Encyclopedic Dictionary of Mathematics (2nd ed.), MIT Press, ISBN 978-0-262-59020-4.
- Ivanov, A.B. (2001) [1994], «Vector», Encyclopedia of Mathematics, EMS Press.
- Kane, Thomas R.; Levinson, David A. (1996), Dynamics Online, Sunnyvale, California: OnLine Dynamics.
- Lang, Serge (1986). Introduction to Linear Algebra (2nd ed.). Springer. ISBN 0-387-96205-0.
- Pedoe, Daniel (1988). Geometry: A comprehensive course. Dover. ISBN 0-486-65812-0.
Physical treatments[edit]
- Aris, R. (1990). Vectors, Tensors and the Basic Equations of Fluid Mechanics. Dover. ISBN 978-0-486-66110-0.
- Feynman, Richard; Leighton, R.; Sands, M. (2005). «Chapter 11». The Feynman Lectures on Physics. Vol. I (2nd ed.). Addison Wesley. ISBN 978-0-8053-9046-9.
External links[edit]
Wikimedia Commons has media related to Vectors.
- «Vector», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Online vector identities (PDF)
- Introducing Vectors A conceptual introduction (applied mathematics)
This article is about the vectors mainly used in physics and engineering to represent directed quantities. For mathematical vectors in general, see Vector (mathematics and physics). For other uses, see Vector (disambiguation).
A vector pointing from A to B
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector[1] or spatial vector[2]) is a geometric object that has magnitude (or length) and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a directed line segment, or graphically as an arrow connecting an initial point A with a terminal point B,[3] and denoted by 
A vector is what is needed to «carry» the point A to the point B; the Latin word vector means «carrier».[4] It was first used by 18th century astronomers investigating planetary revolution around the Sun.[5] The magnitude of the vector is the distance between the two points, and the direction refers to the direction of displacement from A to B. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors,[6] operations which obey the familiar algebraic laws of commutativity, associativity, and distributivity. These operations and associated laws qualify Euclidean vectors as an example of the more generalized concept of vectors defined simply as elements of a vector space.
Vectors play an important role in physics: the velocity and acceleration of a moving object and the forces acting on it can all be described with vectors.[7] Many other physical quantities can be usefully thought of as vectors. Although most of them do not represent distances (except, for example, position or displacement), their magnitude and direction can still be represented by the length and direction of an arrow. The mathematical representation of a physical vector depends on the coordinate system used to describe it. Other vector-like objects that describe physical quantities and transform in a similar way under changes of the coordinate system include pseudovectors and tensors.[8]
History[edit]
The vector concept, as we know it today, is the result of a gradual development over a period of more than 200 years. About a dozen people contributed significantly to its development.[9] In 1835, Giusto Bellavitis abstracted the basic idea when he established the concept of equipollence. Working in a Euclidean plane, he made equipollent any pair of parallel line segments of the same length and orientation. Essentially, he realized an equivalence relation on the pairs of points (bipoints) in the plane, and thus erected the first space of vectors in the plane.[9]: 52–4 The term vector was introduced by William Rowan Hamilton as part of a quaternion, which is a sum q = s + v of a Real number s (also called scalar) and a 3-dimensional vector. Like Bellavitis, Hamilton viewed vectors as representative of classes of equipollent directed segments. As complex numbers use an imaginary unit to complement the real line, Hamilton considered the vector v to be the imaginary part of a quaternion:[10]
The algebraically imaginary part, being geometrically constructed by a straight line, or radius vector, which has, in general, for each determined quaternion, a determined length and determined direction in space, may be called the vector part, or simply the vector of the quaternion.
Several other mathematicians developed vector-like systems in the middle of the nineteenth century, including Augustin Cauchy, Hermann Grassmann, August Möbius, Comte de Saint-Venant, and Matthew O’Brien. Grassmann’s 1840 work Theorie der Ebbe und Flut (Theory of the Ebb and Flow) was the first system of spatial analysis that is similar to today’s system, and had ideas corresponding to the cross product, scalar product and vector differentiation. Grassmann’s work was largely neglected until the 1870s.[9] Peter Guthrie Tait carried the quaternion standard after Hamilton. His 1867 Elementary Treatise of Quaternions included extensive treatment of the nabla or del operator ∇. In 1878, Elements of Dynamic was published by William Kingdon Clifford. Clifford simplified the quaternion study by isolating the dot product and cross product of two vectors from the complete quaternion product. This approach made vector calculations available to engineers—and others working in three dimensions and skeptical of the fourth.
Josiah Willard Gibbs, who was exposed to quaternions through James Clerk Maxwell’s Treatise on Electricity and Magnetism, separated off their vector part for independent treatment. The first half of Gibbs’s Elements of Vector Analysis, published in 1881, presents what is essentially the modern system of vector analysis.[9][6] In 1901, Edwin Bidwell Wilson published Vector Analysis, adapted from Gibb’s lectures, which banished any mention of quaternions in the development of vector calculus.
Overview[edit]
In physics and engineering, a vector is typically regarded as a geometric entity characterized by a magnitude and a direction. It is formally defined as a directed line segment, or arrow, in a Euclidean space.[11] In pure mathematics, a vector is defined more generally as any element of a vector space. In this context, vectors are abstract entities which may or may not be characterized by a magnitude and a direction. This generalized definition implies that the above-mentioned geometric entities are a special kind of vectors, as they are elements of a special kind of vector space called Euclidean space. This particular article is about vectors strictly defined as arrows in Euclidean space. When it becomes necessary to distinguish these special vectors from vectors as defined in pure mathematics, they are sometimes referred to as geometric, spatial, or Euclidean vectors.
Being an arrow, a Euclidean vector possesses a definite initial point and terminal point. A vector with fixed initial and terminal point is called a bound vector.[12] When only the magnitude and direction of the vector matter, then the particular initial point is of no importance, and the vector is called a free vector. Thus two arrows 

Further information[edit]
In classical Euclidean geometry (i.e., synthetic geometry), vectors were introduced (during the 19th century) as equivalence classes under equipollence, of ordered pairs of points; two pairs (A, B) and (C, D) being equipollent if the points A, B, D, C, in this order, form a parallelogram. Such an equivalence class is called a vector, more precisely, a Euclidean vector.[13] The equivalence class of (A, B) is often denoted 
A Euclidean vector is thus an equivalence class of directed segments with the same magnitude (e.g., the length of the line segment (A, B)) and same direction (e.g., the direction from A to B).[14] In physics, Euclidean vectors are used to represent physical quantities that have both magnitude and direction, but are not located at a specific place, in contrast to scalars, which have no direction.[7] For example, velocity, forces and acceleration are represented by vectors.
In modern geometry, Euclidean spaces are often defined from linear algebra. More precisely, a Euclidean space E is defined as a set to which is associated an inner product space of finite dimension over the reals 


Sometimes, Euclidean vectors are considered without reference to a Euclidean space. In this case, a Euclidean vector is an element of a normed vector space of finite dimension over the reals, or, typically, an element of 

The Euclidean space 



Examples in one dimension[edit]
Since the physicist’s concept of force has a direction and a magnitude, it may be seen as a vector. As an example, consider a rightward force F of 15 newtons. If the positive axis is also directed rightward, then F is represented by the vector 15 N, and if positive points leftward, then the vector for F is −15 N. In either case, the magnitude of the vector is 15 N. Likewise, the vector representation of a displacement Δs of 4 meters would be 4 m or −4 m, depending on its direction, and its magnitude would be 4 m regardless.
In physics and engineering[edit]
Vectors are fundamental in the physical sciences. They can be used to represent any quantity that has magnitude, has direction, and which adheres to the rules of vector addition. An example is velocity, the magnitude of which is speed. For instance, the velocity 5 meters per second upward could be represented by the vector (0, 5) (in 2 dimensions with the positive y-axis as ‘up’). Another quantity represented by a vector is force, since it has a magnitude and direction and follows the rules of vector addition.[7] Vectors also describe many other physical quantities, such as linear displacement, displacement, linear acceleration, angular acceleration, linear momentum, and angular momentum. Other physical vectors, such as the electric and magnetic field, are represented as a system of vectors at each point of a physical space; that is, a vector field. Examples of quantities that have magnitude and direction, but fail to follow the rules of vector addition, are angular displacement and electric current. Consequently, these are not vectors.
In Cartesian space[edit]
In the Cartesian coordinate system, a bound vector can be represented by identifying the coordinates of its initial and terminal point. For instance, the points A = (1, 0, 0) and B = (0, 1, 0) in space determine the bound vector 
In Cartesian coordinates, a free vector may be thought of in terms of a corresponding bound vector, in this sense, whose initial point has the coordinates of the origin O = (0, 0, 0). It is then determined by the coordinates of that bound vector’s terminal point. Thus the free vector represented by (1, 0, 0) is a vector of unit length—pointing along the direction of the positive x-axis.
This coordinate representation of free vectors allows their algebraic features to be expressed in a convenient numerical fashion. For example, the sum of the two (free) vectors (1, 2, 3) and (−2, 0, 4) is the (free) vector
Euclidean and affine vectors[edit]
In the geometrical and physical settings, it is sometimes possible to associate, in a natural way, a length or magnitude and a direction to vectors. In addition, the notion of direction is strictly associated with the notion of an angle between two vectors. If the dot product of two vectors is defined—a scalar-valued product of two vectors—then it is also possible to define a length; the dot product gives a convenient algebraic characterization of both angle (a function of the dot product between any two non-zero vectors) and length (the square root of the dot product of a vector by itself). In three dimensions, it is further possible to define the cross product, which supplies an algebraic characterization of the area and orientation in space of the parallelogram defined by two vectors (used as sides of the parallelogram). In any dimension (and, in particular, higher dimensions), it’s possible to define the exterior product, which (among other things) supplies an algebraic characterization of the area and orientation in space of the n-dimensional parallelotope defined by n vectors.
In a pseudo-Euclidean space, a vector’s squared length can be positive, negative, or zero. An important example is Minkowski space (which is important to our understanding of special relativity).
However, it is not always possible or desirable to define the length of a vector. This more general type of spatial vector is the subject of vector spaces (for free vectors) and affine spaces (for bound vectors, as each represented by an ordered pair of «points»). One physical example comes from thermodynamics, where many quantities of interest can be considered vectors in a space with no notion of length or angle.[15]
Generalizations[edit]
In physics, as well as mathematics, a vector is often identified with a tuple of components, or list of numbers, that act as scalar coefficients for a set of basis vectors. When the basis is transformed, for example by rotation or stretching, then the components of any vector in terms of that basis also transform in an opposite sense. The vector itself has not changed, but the basis has, so the components of the vector must change to compensate. The vector is called covariant or contravariant, depending on how the transformation of the vector’s components is related to the transformation of the basis. In general, contravariant vectors are «regular vectors» with units of distance (such as a displacement), or distance times some other unit (such as velocity or acceleration); covariant vectors, on the other hand, have units of one-over-distance such as gradient. If you change units (a special case of a change of basis) from meters to millimeters, a scale factor of 1/1000, a displacement of 1 m becomes 1000 mm—a contravariant change in numerical value. In contrast, a gradient of 1 K/m becomes 0.001 K/mm—a covariant change in value (for more, see covariance and contravariance of vectors). Tensors are another type of quantity that behave in this way; a vector is one type of tensor.
In pure mathematics, a vector is any element of a vector space over some field and is often represented as a coordinate vector. The vectors described in this article are a very special case of this general definition, because they are contravariant with respect to the ambient space. Contravariance captures the physical intuition behind the idea that a vector has «magnitude and direction».
Representations[edit]
Vectors are usually denoted in lowercase boldface, as in 






Vectors are usually shown in graphs or other diagrams as arrows (directed line segments), as illustrated in the figure. Here, the point A is called the origin, tail, base, or initial point, and the point B is called the head, tip, endpoint, terminal point or final point. The length of the arrow is proportional to the vector’s magnitude, while the direction in which the arrow points indicates the vector’s direction.
On a two-dimensional diagram, a vector perpendicular to the plane of the diagram is sometimes desired. These vectors are commonly shown as small circles. A circle with a dot at its centre (Unicode U+2299 ⊙) indicates a vector pointing out of the front of the diagram, toward the viewer. A circle with a cross inscribed in it (Unicode U+2297 ⊗) indicates a vector pointing into and behind the diagram. These can be thought of as viewing the tip of an arrow head on and viewing the flights of an arrow from the back.
A vector in the Cartesian plane, showing the position of a point A with coordinates (2, 3).
In order to calculate with vectors, the graphical representation may be too cumbersome. Vectors in an n-dimensional Euclidean space can be represented as coordinate vectors in a Cartesian coordinate system. The endpoint of a vector can be identified with an ordered list of n real numbers (n-tuple). These numbers are the coordinates of the endpoint of the vector, with respect to a given Cartesian coordinate system, and are typically called the scalar components (or scalar projections) of the vector on the axes of the coordinate system.
As an example in two dimensions (see figure), the vector from the origin O = (0, 0) to the point A = (2, 3) is simply written as
The notion that the tail of the vector coincides with the origin is implicit and easily understood. Thus, the more explicit notation 
In three dimensional Euclidean space (or R3), vectors are identified with triples of scalar components:
also written,
This can be generalised to n-dimensional Euclidean space (or Rn).
These numbers are often arranged into a column vector or row vector, particularly when dealing with matrices, as follows:
Another way to represent a vector in n-dimensions is to introduce the standard basis vectors. For instance, in three dimensions, there are three of them:
These have the intuitive interpretation as vectors of unit length pointing up the x-, y-, and z-axis of a Cartesian coordinate system, respectively. In terms of these, any vector a in R3 can be expressed in the form:
or
where a1, a2, a3 are called the vector components (or vector projections) of a on the basis vectors or, equivalently, on the corresponding Cartesian axes x, y, and z (see figure), while a1, a2, a3 are the respective scalar components (or scalar projections).
In introductory physics textbooks, the standard basis vectors are often denoted 

The notation ei is compatible with the index notation and the summation convention commonly used in higher level mathematics, physics, and engineering.
Decomposition or resolution[edit]
As explained above, a vector is often described by a set of vector components that add up to form the given vector. Typically, these components are the projections of the vector on a set of mutually perpendicular reference axes (basis vectors). The vector is said to be decomposed or resolved with respect to that set.
Illustration of tangential and normal components of a vector to a surface.
The decomposition or resolution[16] of a vector into components is not unique, because it depends on the choice of the axes on which the vector is projected.
Moreover, the use of Cartesian unit vectors such as 


The choice of a basis does not affect the properties of a vector or its behaviour under transformations.
A vector can also be broken up with respect to «non-fixed» basis vectors that change their orientation as a function of time or space. For example, a vector in three-dimensional space can be decomposed with respect to two axes, respectively normal, and tangent to a surface (see figure). Moreover, the radial and tangential components of a vector relate to the radius of rotation of an object. The former is parallel to the radius and the latter is orthogonal to it.[17]
In these cases, each of the components may be in turn decomposed with respect to a fixed coordinate system or basis set (e.g., a global coordinate system, or inertial reference frame).
Basic properties[edit]
The following section uses the Cartesian coordinate system with basis vectors
and assumes that all vectors have the origin as a common base point. A vector a will be written as
Equality[edit]
Two vectors are said to be equal if they have the same magnitude and direction. Equivalently they will be equal if their coordinates are equal. So two vectors
and
are equal if
Opposite, parallel, and antiparallel vectors[edit]
Two vectors are opposite if they have the same magnitude but opposite direction. So two vectors
and
are opposite if
Two vectors are parallel if they have the same direction but not necessarily the same magnitude, or antiparallel if they have opposite direction but not necessarily the same magnitude.
Addition and subtraction[edit]
The sum of a and b of two vectors may be defined as
The resulting vector is sometimes called the resultant vector of a and b.
The addition may be represented graphically by placing the tail of the arrow b at the head of the arrow a, and then drawing an arrow from the tail of a to the head of b. The new arrow drawn represents the vector a + b, as illustrated below:[7]
This addition method is sometimes called the parallelogram rule because a and b form the sides of a parallelogram and a + b is one of the diagonals. If a and b are bound vectors that have the same base point, this point will also be the base point of a + b. One can check geometrically that a + b = b + a and (a + b) + c = a + (b + c).
The difference of a and b is
Subtraction of two vectors can be geometrically illustrated as follows: to subtract b from a, place the tails of a and b at the same point, and then draw an arrow from the head of b to the head of a. This new arrow represents the vector (-b) + a, with (-b) being the opposite of b, see drawing. And (-b) + a = a − b.
Scalar multiplication[edit]
Scalar multiplication of a vector by a factor of 3 stretches the vector out.
A vector may also be multiplied, or re-scaled, by a real number r. In the context of conventional vector algebra, these real numbers are often called scalars (from scale) to distinguish them from vectors. The operation of multiplying a vector by a scalar is called scalar multiplication. The resulting vector is
Intuitively, multiplying by a scalar r stretches a vector out by a factor of r. Geometrically, this can be visualized (at least in the case when r is an integer) as placing r copies of the vector in a line where the endpoint of one vector is the initial point of the next vector.
If r is negative, then the vector changes direction: it flips around by an angle of 180°. Two examples (r = −1 and r = 2) are given below:
The scalar multiplications −a and 2a of a vector a
Scalar multiplication is distributive over vector addition in the following sense: r(a + b) = ra + rb for all vectors a and b and all scalars r. One can also show that a − b = a + (−1)b.
Length[edit]
The length or magnitude or norm of the vector a is denoted by ‖a‖ or, less commonly, |a|, which is not to be confused with the absolute value (a scalar «norm»).
The length of the vector a can be computed with the Euclidean norm,
which is a consequence of the Pythagorean theorem since the basis vectors e1, e2, e3 are orthogonal unit vectors.
This happens to be equal to the square root of the dot product, discussed below, of the vector with itself:
Unit vector[edit]
The normalization of a vector a into a unit vector â
A unit vector is any vector with a length of one; normally unit vectors are used simply to indicate direction. A vector of arbitrary length can be divided by its length to create a unit vector.[14] This is known as normalizing a vector. A unit vector is often indicated with a hat as in â.
To normalize a vector a = (a1, a2, a3), scale the vector by the reciprocal of its length ‖a‖. That is:
Zero vector[edit]
The zero vector is the vector with length zero. Written out in coordinates, the vector is (0, 0, 0), and it is commonly denoted 
Dot product[edit]
The dot product of two vectors a and b (sometimes called the inner product, or, since its result is a scalar, the scalar product) is denoted by a ∙ b, and is defined as:
where θ is the measure of the angle between a and b (see trigonometric function for an explanation of cosine). Geometrically, this means that a and b are drawn with a common start point, and then the length of a is multiplied with the length of the component of b that points in the same direction as a.
The dot product can also be defined as the sum of the products of the components of each vector as
Cross product[edit]
The cross product (also called the vector product or outer product) is only meaningful in three or seven dimensions. The cross product differs from the dot product primarily in that the result of the cross product of two vectors is a vector. The cross product, denoted a × b, is a vector perpendicular to both a and b and is defined as
where θ is the measure of the angle between a and b, and n is a unit vector perpendicular to both a and b which completes a right-handed system. The right-handedness constraint is necessary because there exist two unit vectors that are perpendicular to both a and b, namely, n and (−n).
An illustration of the cross product
The cross product a × b is defined so that a, b, and a × b also becomes a right-handed system (although a and b are not necessarily orthogonal). This is the right-hand rule.
The length of a × b can be interpreted as the area of the parallelogram having a and b as sides.
The cross product can be written as
For arbitrary choices of spatial orientation (that is, allowing for left-handed as well as right-handed coordinate systems) the cross product of two vectors is a pseudovector instead of a vector (see below).
Scalar triple product[edit]
The scalar triple product (also called the box product or mixed triple product) is not really a new operator, but a way of applying the other two multiplication operators to three vectors. The scalar triple product is sometimes denoted by (a b c) and defined as:
It has three primary uses. First, the absolute value of the box product is the volume of the parallelepiped which has edges that are defined by the three vectors. Second, the scalar triple product is zero if and only if the three vectors are linearly dependent, which can be easily proved by considering that in order for the three vectors to not make a volume, they must all lie in the same plane. Third, the box product is positive if and only if the three vectors a, b and c are right-handed.
In components (with respect to a right-handed orthonormal basis), if the three vectors are thought of as rows (or columns, but in the same order), the scalar triple product is simply the determinant of the 3-by-3 matrix having the three vectors as rows
The scalar triple product is linear in all three entries and anti-symmetric in the following sense:
Conversion between multiple Cartesian bases[edit]
All examples thus far have dealt with vectors expressed in terms of the same basis, namely, the e basis {e1, e2, e3}. However, a vector can be expressed in terms of any number of different bases that are not necessarily aligned with each other, and still remain the same vector. In the e basis, a vector a is expressed, by definition, as
The scalar components in the e basis are, by definition,
In another orthonormal basis n = {n1, n2, n3} that is not necessarily aligned with e, the vector a is expressed as
and the scalar components in the n basis are, by definition,
The values of p, q, r, and u, v, w relate to the unit vectors in such a way that the resulting vector sum is exactly the same physical vector a in both cases. It is common to encounter vectors known in terms of different bases (for example, one basis fixed to the Earth and a second basis fixed to a moving vehicle). In such a case it is necessary to develop a method to convert between bases so the basic vector operations such as addition and subtraction can be performed. One way to express u, v, w in terms of p, q, r is to use column matrices along with a direction cosine matrix containing the information that relates the two bases. Such an expression can be formed by substitution of the above equations to form
Distributing the dot-multiplication gives
Replacing each dot product with a unique scalar gives
and these equations can be expressed as the single matrix equation
This matrix equation relates the scalar components of a in the n basis (u,v, and w) with those in the e basis (p, q, and r). Each matrix element cjk is the direction cosine relating nj to ek.[18] The term direction cosine refers to the cosine of the angle between two unit vectors, which is also equal to their dot product.[18] Therefore,
By referring collectively to e1, e2, e3 as the e basis and to n1, n2, n3 as the n basis, the matrix containing all the cjk is known as the «transformation matrix from e to n«, or the «rotation matrix from e to n» (because it can be imagined as the «rotation» of a vector from one basis to another), or the «direction cosine matrix from e to n«[18] (because it contains direction cosines). The properties of a rotation matrix are such that its inverse is equal to its transpose. This means that the «rotation matrix from e to n» is the transpose of «rotation matrix from n to e«.
The properties of a direction cosine matrix, C are:[19]
- the determinant is unity, |C| = 1;
- the inverse is equal to the transpose;
- the rows and columns are orthogonal unit vectors, therefore their dot products are zero.
The advantage of this method is that a direction cosine matrix can usually be obtained independently by using Euler angles or a quaternion to relate the two vector bases, so the basis conversions can be performed directly, without having to work out all the dot products described above.
By applying several matrix multiplications in succession, any vector can be expressed in any basis so long as the set of direction cosines is known relating the successive bases.[18]
Other dimensions[edit]
With the exception of the cross and triple products, the above formulae generalise to two dimensions and higher dimensions. For example, addition generalises to two dimensions as
and in four dimensions as
The cross product does not readily generalise to other dimensions, though the closely related exterior product does, whose result is a bivector. In two dimensions this is simply a pseudoscalar
A seven-dimensional cross product is similar to the cross product in that its result is a vector orthogonal to the two arguments; there is however no natural way of selecting one of the possible such products.
Physics[edit]
Vectors have many uses in physics and other sciences.
Length and units[edit]
In abstract vector spaces, the length of the arrow depends on a dimensionless scale. If it represents, for example, a force, the «scale» is of physical dimension length/force. Thus there is typically consistency in scale among quantities of the same dimension, but otherwise scale ratios may vary; for example, if «1 newton» and «5 m» are both represented with an arrow of 2 cm, the scales are 1 m:50 N and 1:250 respectively. Equal length of vectors of different dimension has no particular significance unless there is some proportionality constant inherent in the system that the diagram represents. Also length of a unit vector (of dimension length, not length/force, etc.) has no coordinate-system-invariant significance.
Vector-valued functions[edit]
Often in areas of physics and mathematics, a vector evolves in time, meaning that it depends on a time parameter t. For instance, if r represents the position vector of a particle, then r(t) gives a parametric representation of the trajectory of the particle. Vector-valued functions can be differentiated and integrated by differentiating or integrating the components of the vector, and many of the familiar rules from calculus continue to hold for the derivative and integral of vector-valued functions.
Position, velocity and acceleration[edit]
The position of a point x = (x1, x2, x3) in three-dimensional space can be represented as a position vector whose base point is the origin
The position vector has dimensions of length.
Given two points x = (x1, x2, x3), y = (y1, y2, y3) their displacement is a vector
which specifies the position of y relative to x. The length of this vector gives the straight-line distance from x to y. Displacement has the dimensions of length.
The velocity v of a point or particle is a vector, its length gives the speed. For constant velocity the position at time t will be
where x0 is the position at time t = 0. Velocity is the time derivative of position. Its dimensions are length/time.
Acceleration a of a point is vector which is the time derivative of velocity. Its dimensions are length/time2.
Force, energy, work[edit]
Force is a vector with dimensions of mass×length/time2 and Newton’s second law is the scalar multiplication
Work is the dot product of force and displacement
Vectors, pseudovectors, and transformations[edit]
An alternative characterization of Euclidean vectors, especially in physics, describes them as lists of quantities which behave in a certain way under a coordinate transformation. A contravariant vector is required to have components that «transform opposite to the basis» under changes of basis. The vector itself does not change when the basis is transformed; instead, the components of the vector make a change that cancels the change in the basis. In other words, if the reference axes (and the basis derived from it) were rotated in one direction, the component representation of the vector would rotate in the opposite way to generate the same final vector. Similarly, if the reference axes were stretched in one direction, the components of the vector would reduce in an exactly compensating way. Mathematically, if the basis undergoes a transformation described by an invertible matrix M, so that a coordinate vector x is transformed to x′ = Mx, then a contravariant vector v must be similarly transformed via v′ = M
In the language of differential geometry, the requirement that the components of a vector transform according to the same matrix of the coordinate transition is equivalent to defining a contravariant vector to be a tensor of contravariant rank one. Alternatively, a contravariant vector is defined to be a tangent vector, and the rules for transforming a contravariant vector follow from the chain rule.
Some vectors transform like contravariant vectors, except that when they are reflected through a mirror, they flip and gain a minus sign. A transformation that switches right-handedness to left-handedness and vice versa like a mirror does is said to change the orientation of space. A vector which gains a minus sign when the orientation of space changes is called a pseudovector or an axial vector. Ordinary vectors are sometimes called true vectors or polar vectors to distinguish them from pseudovectors. Pseudovectors occur most frequently as the cross product of two ordinary vectors.
One example of a pseudovector is angular velocity. Driving in a car, and looking forward, each of the wheels has an angular velocity vector pointing to the left. If the world is reflected in a mirror which switches the left and right side of the car, the reflection of this angular velocity vector points to the right, but the actual angular velocity vector of the wheel still points to the left, corresponding to the minus sign. Other examples of pseudovectors include magnetic field, torque, or more generally any cross product of two (true) vectors.
This distinction between vectors and pseudovectors is often ignored, but it becomes important in studying symmetry properties. See parity (physics).
See also[edit]
- Affine space, which distinguishes between vectors and points
- Array (data structure)
- Banach space
- Clifford algebra
- Complex number
- Coordinate system
- Covariance and contravariance of vectors
- Four-vector, a non-Euclidean vector in Minkowski space (i.e. four-dimensional spacetime), important in relativity
- Function space
- Grassmann’s Ausdehnungslehre
- Hilbert space
- Normal vector
- Null vector
- Position (geometry)
- Pseudovector
- Quaternion
- Tangential and normal components (of a vector)
- Tensor
- Unit vector
- Vector bundle
- Vector calculus
- Vector notation
- Vector-valued function
Notes[edit]
- ^ Ivanov 2001
- ^ Heinbockel 2001
- ^ Itô 1993, p. 1678; Pedoe 1988
- ^ Latin: vectus, perfect participle of vehere, «to carry»/ veho = «I carry». For historical development of the word vector, see «vector n.«. Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.) and Jeff Miller. «Earliest Known Uses of Some of the Words of Mathematics». Retrieved 2007-05-25.
- ^ The Oxford English Dictionary (2nd. ed.). London: Clarendon Press. 2001. ISBN 9780195219425.
- ^ a b «vector | Definition & Facts». Encyclopedia Britannica. Retrieved 2020-08-19.
- ^ a b c d «Vectors». www.mathsisfun.com. Retrieved 2020-08-19.
- ^ Weisstein, Eric W. «Vector». mathworld.wolfram.com. Retrieved 2020-08-19.
- ^ a b c d Michael J. Crowe, A History of Vector Analysis; see also his «lecture notes» (PDF). Archived from the original (PDF) on January 26, 2004. Retrieved 2010-09-04. on the subject.
- ^ W. R. Hamilton (1846) London, Edinburgh & Dublin Philosophical Magazine 3rd series 29 27
- ^ Itô 1993, p. 1678
- ^ Formerly known as located vector. See Lang 1986, p. 9.
- ^ In some old texts, the pair (A, B) is called a bound vector, and its equivalence class is called a free vector.
- ^ a b «1.1: Vectors». Mathematics LibreTexts. 2013-11-07. Retrieved 2020-08-19.
- ^ Thermodynamics and Differential Forms
- ^ Gibbs, J.W. (1901). Vector Analysis: A Text-book for the Use of Students of Mathematics and Physics, Founded upon the Lectures of J. Willard Gibbs, by E.B. Wilson, Chares Scribner’s Sons, New York, p. 15: «Any vector r coplanar with two non-collinear vectors a and b may be resolved into two components parallel to a and b respectively. This resolution may be accomplished by constructing the parallelogram …»
- ^ «U. Guelph Physics Dept., «Torque and Angular Acceleration»«. Archived from the original on 2007-01-22. Retrieved 2007-01-05.
- ^ a b c d Kane & Levinson 1996, pp. 20–22
- ^ M., Rogers, Robert (2007). Applied mathematics in integrated navigation systems (3rd ed.). Reston, Va.: American Institute of Aeronautics and Astronautics. ISBN 9781563479274. OCLC 652389481.
References[edit]
Mathematical treatments[edit]
- Apostol, Tom (1967). Calculus. Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra. Wiley. ISBN 978-0-471-00005-1.
- Apostol, Tom (1969). Calculus. Vol. 2: Multi-Variable Calculus and Linear Algebra with Applications. Wiley. ISBN 978-0-471-00007-5.
- Heinbockel, J. H. (2001), Introduction to Tensor Calculus and Continuum Mechanics, Trafford Publishing, ISBN 1-55369-133-4.
- Itô, Kiyosi (1993), Encyclopedic Dictionary of Mathematics (2nd ed.), MIT Press, ISBN 978-0-262-59020-4.
- Ivanov, A.B. (2001) [1994], «Vector», Encyclopedia of Mathematics, EMS Press.
- Kane, Thomas R.; Levinson, David A. (1996), Dynamics Online, Sunnyvale, California: OnLine Dynamics.
- Lang, Serge (1986). Introduction to Linear Algebra (2nd ed.). Springer. ISBN 0-387-96205-0.
- Pedoe, Daniel (1988). Geometry: A comprehensive course. Dover. ISBN 0-486-65812-0.
Physical treatments[edit]
- Aris, R. (1990). Vectors, Tensors and the Basic Equations of Fluid Mechanics. Dover. ISBN 978-0-486-66110-0.
- Feynman, Richard; Leighton, R.; Sands, M. (2005). «Chapter 11». The Feynman Lectures on Physics. Vol. I (2nd ed.). Addison Wesley. ISBN 978-0-8053-9046-9.
External links[edit]
Wikimedia Commons has media related to Vectors.
- «Vector», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Online vector identities (PDF)
- Introducing Vectors A conceptual introduction (applied mathematics)
Векторы в физике
В физике огромную роль играют векторные величины, то есть те величины, которые имеют кроме численного значения ещё и какое-то направление. Это такие величины как скорость, электрическое поле, сила, и т. д.
Векторная природа этих величин ― важнейший аспект, который нельзя опустить на экзамене. Дело в том, что для успешной сдачи экзамена необходима правильная работа с векторами, поскольку встречаться они будут много и часто.
Первое, что нам понадобится ― научиться складывать вектора.
Сложение векторов
В физике все вектора, которые будет необходимо складывать, будут складываться по правилу параллелограмма. Рассмотрим, как оно работает. Если есть два вектора, которые нужно сложить
То сначала мы должны достроить эти вектора до параллелограмма:
Тогда получившаяся диагональ будет являться суммарным вектором, который мы и хотели найти.
Частным случаем сложения векторов является
расположение векторов на одной прямой с началом в одной точке:
При таком расположении сложно использовать стандартные правила сложения, поэтому намного проще укоротить оба вектора на одну и ту же длину, в частности – на длину более короткого вектора. Результатом этой операции как раз получится сумма двух этих векторов:
Обратная ситуация — два вектора имеют общее начало и направлены в одну сторону
Сумма этих векторов — вектор, направленный в ту же сторону и равный по длине сумме длин изначальных векторов:
Для решения численных заданий будет необходимо подставлять определённые значения в полученные формулы.
Дело в том, что работать с векторными величинами невозможно, поэтому часто (особенно в задачах механики) будет необходимо делать проекции векторов.
Проекции ― это второй навык, которым необходимо овладеть, чтобы успешно справляться с задачами экзамена.
Проекция векторов
Если вектор наклонён к некоторой оси под углом α:
То чтобы получить прилежащую проекцию (проекцию на ось Х):
Нужно умножить модуль вектора на косинус,
ax = a∙cosα.
Чтобы получить противолежащую проекцию (проекцию на ось Y).
Нужно умножить модуль вектора на синус,
ay = a∙sinα.
В этой главе…
- Изучаем сложение и вычитание векторов
- Выражаем векторы через координаты
- Разбиваем векторы на компоненты
- Выражаем перемещение, ускорение и скорость в виде векторов
- Определяем изменение скорости под действием тяготения
Довольно трудно добраться в место назначения — пешком ли, на велосипеде ли, на автомобиле ли, на самолете ли — если вы не знаете направления движения. Для успеха путешествия нужно знать не только расстояние, но и направление движения. В главе 3 описывались такие понятия, как перемещение, скорость и ускорение, связанные некоторыми соотношениями, как, например, ( s={}^1!/!_2at^2+v_0t ). С помощью таких соотношений можно получить значения для ускорения, например 27 метров в секунду в квадрате, или для скорости, например 42,7 мили в час. Конечно, полезно знать эти параметры движения, но что можно сказать о направлении движения?
В реальном мире просто необходимо знать направление движения. Именно векторы обозначают такое направление. Очень многие люди ошибочно считают векторы очень сложными объектами, но это совсем не так. В этой главе вы узнаете, насколько легко и просто можно обращаться с ними при решении задач.
Содержание
- Осваиваем векторы
- Определяем направление: основные свойства векторов
- Комбинируем направления: сложение векторов
- Вычисляем разницу расстояний: разность векторов
- Облекаем векторы в числа
- Разбиение вектора на компоненты
- Ищем компоненты вектора по заданной величине и углу
- Находим величину и направление вектора по его компонентам
- Срываем покров с векторов
- Перемещение — тоже вектор
- Скорость — еще один вектор
- Ускорение — еще один вектор
- Упражнение со скоростью: скользим по радуге
Осваиваем векторы
В главе 3 мы работали с простыми числами или измерениями, которые в физике называются величинами. Например, в результате измерения перемещения на 3 метра получена величина перемещения 3 метра. Вектор отличается от величины еще и наличием направления. В повседневной жизни на вопрос о пути понятие “вектор” возникает в виде следующего ответа встречного человека: “Это в 15 милях отсюда”. При этом величина вектора равна 15 милям, а направление вектора определяется взмахом руки. Когда вы навешиваете дверь на петли, то порой слышите совет: “Толкните сильнее влево”. Вот вам еще один вектор! Когда вы объезжаете препятствие на дороге, вам приходится ускоряться и замедляться в разных направлениях. Вот еще несколько векторов!
Векторы встречаются в обыденных ситуациях, например в дорожных указателях, инструкциях по сборке или даже при попытке избежать столкновения со встречным. Поскольку физика стоит за всеми событиями повседневной жизни, то не удивительно, что многие физические концепции, например скорость, ускорение, сила, являются векторами. По этой причине следует поближе познакомиться с векторами, поскольку они присутствуют во всех разделах физики. Вектор — это фундаментальное понятие физики.
Определяем направление: основные свойства векторов
При работе с векторами нужно иметь в виду его направление и величину. Физический параметр без направления, а только с величиной называется скаляром. Если к скаляру добавить направление, то получим вектор.
Визуально в физических задачах вектор отображается в виде стрелки. Действительно, стрелка имеет величину (т.е. длину) и направление (т.е. острие). Взгляните на рис. 4.1. Эта стрелка и есть вектор с началом в тупом конце и с окончанием — в заостренном конце.
Векторы можно использовать для представления силы, ускорения, скорости и других физических параметров. В физике для обозначения векторов используют полужирное начертание, например A. В некоторых книгах векторы обозначают стрелкой над символом, например ( overrightarrow{A} ) . Стрелка обозначает, что у данного параметра A, помимо величины, есть также направление.
Допустим, какой-то умник предложит вам дать пример вектора. Проще простого! Достаточно сказать, что у некого вектора А есть некая величина и некоторое направление. Убежден, что это произведет на умника оглушительное впечатление! Например, скажите, что вектор А направлен под углом 15° к горизонтали и имеет величину 12 метров в секунду. Итак, любопытный умник получит исчерпывающую информацию о векторе А.
На рис. 4.2 показаны два вектора, А и В. Они очень похожи, поскольку обладают одинаковой длиной и направлением. Фактически оба эти вектора равны. Если два вектора равны по величине и направлению, то они считаются равными, т.е. А = В.
Очень скоро читатель станет настоящим экспертом в области векторов. Уже сейчас нам известно, что, когда мы встречаемся с символом А, это значит, что данный параметр обладает величиной и направлением, т.е. является вектором, а два вектора считаются равными, если они имеют одинаковую величину и направление. Но это еще далеко не все. Допустим, чтобы найти нужный вам отель, нужно проехать 20 миль к северу, а потом 20 миль на восток. Так насколько далеко и в каком направлении находится этот отель?
Комбинируем направления: сложение векторов
Два вектора можно сложить и получить результирующий вектор, который является суммой обоих векторов и определяет расстояние и направление до цели.
Допустим, что прохожий говорит вам, что для достижения пункта назначения вам нужно сначала следовать вектору А, а потом вектору В. Так где же находится в этом случае ваш пункт назначения? Сначала нужно проехать по пути, указанному вектором А, а потом по пути, указанному вектором В, как показано на рис. 4.3.
Когда вы доберетесь до конца вектора В, насколько далеко вы будете находиться от исходной точки? Для ответа на этот вопрос начертим еще один вектор С от исходной точки и до конечной точки путешествия, как показано на рис. 4.4.
Новый вектор С представляет собой результат всего путешествия от начала и до самого конца. Все, что нужно сделать, чтобы получить его, так это начертить оба вектора А и В и соединить новым результирующим вектором С.
Сумма векторов достигается за счет того, что начало одного вектора помещается в конец другого, т.е. суммарный вектор проходит от начала одного до конца другого вектора. Иначе говоря, С = А + В. При этом С называется суммой векторов, результатом сложения векторов, или результирующим вектором. Не думайте, что этим ограничиваются возможности комбинирования векторов, ведь векторы можно и вычитать.
Вычисляем разницу расстояний: разность векторов
А что если некто предложит вам векторы С и А, показанные на рис. 4.4, и попросит найти их разность? Их разностью является вектор В, поскольку при сложении векторов А и В получается вектор С. Чтобы объяснить эту мысль, нужно прояснить смысл вычитания вектора А из вектора С: т.е. смысл операции С — А.
Для вычитания двух векторов нужно расположить вместе основания векторов (т.е. концы векторов без остриев), а не совмещать основание одного вектора и острие другого вектора, как при сложении векторов. Затем нужно провести результирующий вектор, который является разностью двух векторов, от острия вычитающего вектора (А) к острию вычитаемого вектора (С). На рис. 4.5 показан пример вычитания вектора А из вектора С (иначе говоря, приведен пример С — А). Как видите, результат такого вычитания равен вектору В, поскольку С = А + В.
Еще один (и для некоторых более простой) способ вычитания векторов заключается в обращении направления второго вектора (т.е. вектора А в разности С — А) и сложении двух векторов: вектора С и обращенного вектора А (т.е. совмещении острия обращенного вектора А с основанием вектора С с последующим проведением результирующего вектора от основания обращенного вектора А к острию вектора С).
Как видите, сложение и вычитание векторов может происходить с одними и теми же векторами в одной задаче. На самом деле с векторами можно выполнять и некоторые другие математические операции. Изложенный выше материал означает, что с векторами можно оперировать так же, как со скалярами, например С = А + В, С — А = В и т.д. Как видите, векторы очень похожи на числа.
Облекаем векторы в числа
Векторы удобно представлять в виде стрелок, но это не всегда самый точный способ работы с ними. Векторы гораздо точнее можно характеризовать числами. Рассмотрим пример сложения векторов А + В, показанных на рис. 4.6.
Предположим, что измерения на рис. 4.6 даны в метрах. Это значит, что вектор А направлен на 1 метр вверх и на 5 метров вправо, а вектор В направлен на 1 метр вправо и на 4 метра вверх. Для получения параметров результирующего вектора С нужно сложить горизонтальные измерения обоих векторов и отдельно сложить вертикальные измерения обоих векторов.
Результирующий вектор С направлен на 6 метров вправо и на 5 метров вверх. Как видите, для получения вертикального измерения вектора С нужно сложить вертикальное измерение вектора А и вертикальное измерение вектора В. А для получения горизонтального измерения вектора С нужно сложить горизонтальное измерение вектора А и горизонтальное измерение вектора В.
Если процедура сложения векторов все еще очень туманна для вас, то тогда можно использовать другую систему обозначений векторов. Поскольку вектор А “простирается” на 5 метров вправо (в положительном направлении оси X) и на 1 метр вверх (в положительном направлении оси Y), то его можно выразить в координатах (х,у), например А = (5;1). Аналогично, поскольку вектор В “простирается” на 1 метр вверх (в положительном направлении оси X) и на 4 метра вправо (в положительном направлении оси Y), то его можно выразить в координатах (х,у), например В = (1;4).
С помощью такой системы обозначений сложение векторов существенно упрощается. Итак, для сложения двух векторов достаточно сложить их координаты по осям X и Y, чтобы получить координаты результирующего вектора по осям X и Y:
Получается, что весь секрет сложения векторов заключается в разбиении каждого вектора на координаты по осям X и Y с последующим их сложением, чтобы соответственно получить координаты X и Y результирующего вектора? Конечно, работа с этими числами для получения координат X и Y результирующего вектора требует некоторых усилий, но они достаточно просты, чтобы с успехом их выполнить.
Допустим, что нужный вам отель находится на расстоянии 20 миль к северу и на расстоянии 20 миль на восток. Как будет выглядеть вектор, направленный из исходной точки к этому отелю? С помощью координатного представления эта задача решается очень легко. Допустим, что положительное направление оси X направлено на восток, а положительное направление оси Y — на север. На первом этапе нужно проехать 20 миль на север, а на втором этапе — 20 миль на восток. В векторном представлении эта задача формулируется следующим образом (восток [X]; север [Y]):
Чтобы сложить эти два вектора, нужно сложить их координаты по соответствующим осям:
Результирующий вектор, который указывает на отель, имеет вид (20; 20).
Рассмотрим еще один пример удачного применения такого представления векторов. Допустим, что вы едете на гоночном автомобиле со скоростью 150 миль в час на восток и видите в зеркало заднего вида приближающегося соперника. Нет проблем, нужно лишь удвоить скорость:
Теперь вы уже не едете, а почти “летите” со скоростью 300 миль в час, но в том же направлении. Итак, в этой задаче демонстрируется процедура умножения вектора на скаляр.
Разбиение вектора на компоненты
Формулировки задач по физике с использованием векторов не всегда так просты, как предыдущие примеры с манипуляциями векторов. Рассмотрим первый вектор на рис. 4.1 с координатами (4; 1) и сравним его со следующей типичной формулировкой физической задачи: найти время перемещения шара со скоростью 7 метров в секунду по наклонной плоскости с длиной основания 1 м, расположенной под углом 15°. С помощью дальнейшей информации в этом разделе вы научитесь находить компоненты векторов и легко и просто манипулировать ими.
Ищем компоненты вектора по заданной величине и углу
Чтобы определить координаты вектора, нужно научиться разбивать векторы на части, которые называются компонентами. Например для вектора (4; 1) Х-компонентой является число 4, а Y-компонентой — число 1.
Часто в физической задаче задается угол и величина вектора, а его компоненты нужно определить. В предыдущем примере известно, что шар катится со скоростью 7 метров в секунду по наклонной плоскости с длиной основания 1 м, расположенной под углом 15°. Для определения времени перемещения шара от одного конца плоскости к другому нам потребуется разобраться только с Х-компонентой. То есть, задача сводится к определению времени перемещения на расстояние 1 метр вдоль оси X. Для ответа на этот вопрос нужно определить скорость перемещения шара по оси X.
Итак, нам известно, что шар движется со скоростью 7 метров в секунду под углом 15° к горизонтали (т.е. положительного направления оси X). В данной формулировке скорость является вектором ( mathbf{v} ) с величиной 7 метров в секунду и направлением 15° к горизонтали.
Теперь нам нужно определить Х-компоненту вектора скорости шара, чтобы определить скорость перемещения шара вдоль основания наклонной плоскости. Х-компонента скорости является скаляром (т.е. имеет только значение, а не значение, направление и точку приложения, как вектор) и обозначается как ( v_x ). Аналогично, Y-компонента скорости шара также является скаляром и обозначается как ( v_y ). Итак, вектор скорости можно выразить через его компоненты:
Именно так выражается разложение вектора на компоненты. Так чему же равны компонента ( v_x ) и компонента ( v_y )? Скорость имеет величину ( v ) (7 метров в секунду) и направление ( theta ) (угол 15° к горизонтали). Также нам известна длина основания наклонной плоскости (1,0 метр). На рис. 4.7 показана схема тригонометрических функций (о, Боже, только не это!), которые описывают направление вектора скорости и помогут нам определить его компоненты. Не стоит волноваться: тригонометрические соотношения не так уж и сложны, если известен угол ( theta ), показанный на рис. 4.7. Величина (или модуль) вектора ( mathbf{v} ) равна ( v ) (иногда если вектор обозначается символом ( v ), то его модуль обозначают символом ( overline{v} )), а его компоненты определяются с помощью рис. 4.7:
Рекомендуется хорошенько запомнить указанные выше выражения для компонент вектора, поскольку нам придется довольно часто встречаться с ними в курсе физики.
Теперь можно пойти немного дальше и попробовать связать отдельные стороны треугольника на рис. 4.7. Это можно легко сделать, если вспомнить соотношение для тангенса ( tg,theta=sintheta/costheta ) и воспользоваться соотношениями для компонент скорости:
Зная соотношение ( v_x=vcostheta ), можно найти величину Х-компоненты скорости шара ( v_x=vcostheta ):
Подставляя числа, получим
Итак, теперь мы знаем, что горизонтальная скорость шара равна 6,7 метров в секунду. Поскольку длина основания наклонной плоскости равна 1,0 метра, то это расстояние шар преодолеет за время:
Таким образом, благодаря тому, что мы научились определять компоненту скорости, нам удалось легко найти решение все задачи: шару потребуется 0,15 секунды для перемещения вдоль наклонной плоскости. А чему равна Y-компонента скорости? Это можно очень легко определить, поступая аналогично:
Находим величину и направление вектора по его компонентам
Иногда требуется определить угол наклона вектора, если известны его компоненты. Например, предположим, что вы ищите отель, расположенный на 20 миль к северу и на 20 миль к востоку. Под каким углом нужно двигаться к нему и насколько далеко он находится? Условия этой задачи можно записать с помощью уже известных нам векторных обозначений (см. предыдущий раздел):
После сложения этих двух векторов получим следующий результат:
Результирующий вектор, который указывает на отель, имеет вид (20; 20). Это еще один способ указания вектора с помощью его компонент. Итак, вернемся к прежнему вопросу: под каким углом нужно двигаться к отелю и насколько далеко он находится от текущего положения? Иначе говоря, глядя на рис. 4.8, прежний вопрос теперь звучит так: “Чему равны ( h ) и ( theta )?”
Найти ( h ) не так уж и трудно, пользуясь теоремой Пифагора:
Подставляя численные значения, получим:
Итак, отель находится на расстоянии 28,3 мили. А под каким углом ( theta ) нужно ехать к нему по прямой? Пользуясь основными тригонометрическими соотношениями, можно записать:
Иначе говоря:
Теперь для определения угла нужно использовать функции, обратные синусу и косинусу:
(Строго говоря, обратной синусу функцией является функция “арксинус”, или ( arcsin(x) ), а обратной косинусу — “арккосинус”, или ( arccos(x) ). Обозначения ( sin^{-1}(x) ) и ( cos^{-1}(x) ) часто используются для обозначения функций “арксинус” и “арккосинус”, но их не рекомендуется употреблять, чтобы не путать с функциями ( 1/sin(x) ) и ( 1/cos(x) ). — Примеч. ред.)
Как вычислить значения функций, обратных синусу (( sin^{-1} )) и косинусу (( cos^{-1} ))? Очень просто, ведь в любом инженерном калькуляторе есть кнопки для таких функций! (Например, в программе Калькулятор операционной системы Windows достаточно ввести число, установить флажок параметра Inv (Обратная) и щелкнуть на кнопке sin (Синус). — Примеч. ред.) Достаточно ввести число и нажать соответствующую кнопку, если таковая имеется, например с надписью arcsin (арксинус). В данном случае для угла ( theta ) получим следующий результат вычислений:
Итак, отель находится на расстоянии 28,3 мили и под углом 45°. Вот так, легко и просто мы успешно решили еще одну физическую задачу!
Аналогично, можно определить угол ( theta ) без необходимости промежуточного вычисления ( h ) с помощью других сведений из тригонометрии:
(Строго говоря, обратной тангенсу функцией является функция “арктангенс”, или ( arctg(x) ). Обозначение ( tg^{-1}(x) ) часто используется для обозначения функции “арктангенс”, но его не рекомендуется употреблять, чтобы не путать с функцией ( 1/tg(x) ). — Примеч. ред.)
Срываем покров с векторов
У нас есть два способа описания векторов для решения физических задач. Первый основан на использовании компонент по осям X и Y, а второй — на величине (модуле) и направлении вектора (угол обычно задается в градусах от 0° до 360°, где угол 0° соответствует направлению вдоль положительного направления оси X). Знание правил взаимного преобразования этих двух способов описания имеет очень большое значение, поскольку для операций с векторами удобно использовать компоненты вектора, а в формулировке физических задач обычно задаются величины и углы векторов.
Вот как выглядит формула преобразования двух способов описания векторов:
В этом уравнении предполагается, что ( theta ) — это угол между горизонтальной компонентой и гипотенузой ( h ) (т.е. самой длинной стороной прямоугольного треугольника, расположенного напротив прямого угла), как показано на рис. 4.8. Если угол не известен, то его можно вывести, если запомнить, что сумма всех углов треугольника равна 180°, а в прямоугольном треугольнике, если вычесть величину прямого угла 90°, то сумма остальных двух углов равна 90°.
Если вам известны компоненты (х,у), то его величину и направление можно определить по следующим формулам:
Такого рода преобразования нужно уметь легко выполнять, поскольку они довольно часто встречаются в задачах. На этом месте часто многие приходят в растерянность и не могут освоить дальнейший материал именно потому, что не овладели простыми правилами разложения вектора на компоненты.
Перемещение — тоже вектор
Перемещение ( s ) следует обозначать ( mathbf{s} ), как вектор с определенной величиной и направлением (для обозначения векторов иногда используют стрелку, которая располагается над именем переменной, например ( overrightarrow{s} ) ). В реальном мире очень важно знать не только величину, но и направление перемещения.
Допустим, что сбылись ваши детские мечты и вы стали звездой бейсбола. Вот вам нужно стремглав бежать к первой базе на расстоянии 90 футов по прямой. Но в каком направлении находится первая база? Допустим, что она находится под углом 45°, как показано на рис. 4.9. Тогда вектор вашего перемещения ( mathbf{s} ) имеет величину 90 футов и направление 45°. А какими будут компоненты этого вектора? Это очень просто:
Скорость — еще один вектор
Представьте себе, что вы бежите к первой базе с вектором перемещения s с величиной 90 футов и направлением 45° по отношению к оси X. Тут стоило бы задаться вопросом: “Позволит мне моя скорость опередить игрока на первой базе?” Хороший вопрос. Достанем калькулятор и подсчитаем скорость, если известно, что для достижения первой базы вам требуется 3 секунды. Для определения скорости нужно поделить величину вектора ( mathbf{s} ) на это время:
В этом выражении вектор перемещения делится на скаляр времени. Результатом такого деления является тоже вектор, а именно вектор скорости:
Итак, ваша скорость равна 30 футам в секунду под углом 45° и эта скорость является вектором ( mathbf{v} ). Деление вектора на скаляр дает вектор другой величины, но такого же направления. В данном примере деление вектора перемещения ( mathbf{s} ) на скаляр времени дает в результате вектор ( mathbf{v} ). Он имеет такую же величину, что и величина перемещения, деленная на величину времени, но теперь вектор ( mathbf{v} ) также имеет определенное направление, которое определяется направлением вектора перемещения ( mathbf{s} ). Итак, в данном примере мы научились манипулировать с векторами, как со скалярами в главе 3, и получать вектор в результате этих манипуляций.
Допустим, что после этих вычислений вы пришли к выводу, что такой скорости недостаточно, чтобы опередить соперника. Ну что ж, нужно срочно изменить направление!
Ускорение — еще один вектор
Что произойдет, если в процессе движения внезапно изменить направление? Вы сразу же почувствуете изменение скорости, а значит, ощутите ускорение. Как и скорость, ускорение ( mathbf{a} ) является вектором.
Предположим, что в предыдущем примере нужно изменить скорость Y-компоненты скорости до величины 25 футов в секунду, чтобы избежать встречи с соперником, причем вам известно, что вы способны отклониться от курса на 90° с ускорением 60 футов в секунду в квадрате (в отчаянной попытке увильнуть от соперника). Достаточно ли этого ускорения для изменения скорости за ту долю секунды, которая отделяет вас от встречи с соперником?
Разница конечного ( t_1 ) и начального ( t_0 ) момента времени равняется изменению времени ( Delta t ). Теперь изменение скорости легко найти по следующей формуле:
Теперь попробуем вычислить изменение скорости от исходной скорости на основе данных на рис. 4.10.
Для поиска конечного значения скорости ( mathbf{v_1} ) нужно выполнить операцию сложения векторов. Это значит, что нужно разложить на компоненты вектор исходной скорости ( mathbf{v_0} ) и вектор изменения скорости ( Delta v ). Вот как выглядят компоненты исходной скорости ( mathbf{v_0} ):
Полпути пройдено. Итак, чему равно изменение скорости ( Delta!mathbf{v} )? Известно, что ( Delta!mathbf{v}=mathbf{a}Deltamathbf{t} ), а ( mathbf{a} ) = 60 футов в секунду2 под углом 90° к прежнему направлению движения, как показано на рис. 4.10. Итак, подсчитаем величину изменения скорости ( Delta!mathbf{v} ) по формуле ( Delta!mathbf{v}=mathbf{a}Deltamathbf{t} ):
Но что можно сказать о направлении ( Delta!mathbf{v} )? Если взглянуть на рис. 4.10, то можно увидеть, что изменение скорости ( Delta!mathbf{v} ) направлено под углом 90° к текущему направлению движения, которое ориентировано под углом 45° к положительному направлению оси X. Следовательно, изменение скорости ( Delta!mathbf{v} ) направлено под углом 135° к положительному направлению оси X. Теперь можно получить выражение для компонент вектора изменения скорости ( Delta!mathbf{v} ):
Теперь остается только выполнить сложение векторов для поиска конечной скорости:
Итак, получен результат ( mathbf{v_1} ) = (17,0 фута в секунду; 25,4 фута в секунду). Y-компонента конечной скорости больше необходимой величины, которая равна 25,0 фута в секунду. После завершения этих вычислений можно спрятать калькулятор и смело выполнить запланированный вираж. Представьте себе, что к изумлению окружающих вам удалось уклониться от соперника и успешно достигнуть места назначения — первой базы (какой крутой поворот вам пришлось для этого выполнить!). Болельщики изумлены и приветствуют вас, а вы, небрежно касаясь кепки кончиками пальцев, отдаете им честь, зная, что все это стало возможным благодаря превосходному знанию физики. После затишья вы украдкой бросаете взгляд на вторую базу: а не закрепить ли успех и попробовать добежать до второй базы? Для этого снова придется достать калькулятор и определить компоненты векторов.
Именно так нужно работать с векторами разных физических параметров: перемещения, скорости и ускорения. Теперь, обладая такими знаниями, можно перевести скалярные уравнения из главы 3 в векторную форму, например, вот так:
Обратите внимание, что полный вектор перемещения — это комбинация перемещения с начальной скоростью и перемещения с постоянным ускорением.
Упражнение со скоростью: скользим по радуге
Хотя сила гравитации подробно описывается в главе 6, но здесь мы рассмотрим результат действия этой силы на небольшом примере с векторами в двух измерениях. Представьте себе, что мячик для игры в гольф движется по горизонтальной вершине скалы со скоростью 1,0 м/с и вскоре сорвется с края скалы на высоте 5 метров от поверхности Земли, как показано на рис. 4.11. Насколько далеко улетит мячик и с какой скоростью он столкнется с поверхностью Земли? В этой задаче прежде всего нужно определить время движения мячика.
Приступим к сбору фактов. Нам известно, что компоненты скорости мячика равны (1; 0), и он находится на высоте 5 метров от поверхности Земли. В процессе падения под действием силы тяготения Земли он движется с постоянным ускорением, ( g ), величина которого равна около 9,8 м/с2.
Итак, как определить, насколько далеко он упадет от края скалы? Один из способов решения этой задачи основан на определении времени движения мячика до столкновения с поверхностью Земли. Поскольку мячик ускоряется только в направлении оси Y (т.е. вертикально вниз), а его компонента скорости по оси X, ( v_x ), не меняется, то пройденное по горизонтали расстояние до столкновения будет равно ( v_xt ), где ( t ) — время движения мячика до столкновения. Сила тяготения ускоряет мячик по вертикали, а значит, перемещение по вертикали (т.е. вдоль оси Y) равно:
В данном случае перемещение по вертикали ( s_y ) = 5 метров, а ускорение ( a_y ) = ( g ) = 9,8 м/с2. Поэтому предыдущее уравнение принимает вид:
Это значит, что время движения мячика до столкновения равно:
Итак, мы вычислили, что мячик будет находиться в полете 1,0 секунды. Отлично, явный прогресс! Поскольку компонента скорости мячика по оси X не изменялась в течение этого времени, то можно легко вычислить расстояние, которое пролетит мячик по горизонтали (т.е. вдоль оси X) за это время:
Подставляем числа и получаем:
Итак, мячик столкнется с поверхностью Земли на расстоянии 1,0 метра по горизонтали.
Теперь можно приступать ко второму вопросу задачи: попробуем определить скорость мячика в момент столкновения с поверхностью Земли. Частично ответ на этот вопрос мы уже знаем, поскольку компонента скорости мячика по оси X не изменялась. Однако по вертикали сила тяготения ускорила мячик по вертикали (т.е. вдоль оси Y), а потому компоненты конечной скорости имеют следующий вид: (1,0; ?). Итак, нам нужно определить величину компоненты скорости мячика по оси Y, обозначенной вопросительным знаком. Воспользуемся следующим соотношением для компоненты скорости по вертикали:
В данном случае начальная скорость ( v_{y0} ) = 0, постоянное ускорение ( a_y=g ) и нужно определить только конечную скорость ( v_{y1} ). Поэтому предыдущее уравнение приобретает следующий вид:
Подставляем числа и получаем:
Ускорение свободного падения, ( g ), также является вектором ( mathbf{g} ). Он направлен к центру Земли, т.е. в отрицательном направлении оси Y, а на поверхности Земли его величина равна около -9,8 м/с2.
Отрицательный знак здесь обозначает направление вниз вектора ( mathbf{g} ), т.е. в отрицательном направлении оси Y. Итак, подставляем обновленное значение ускорения и получаем:
Итак, компоненты конечной скорости мячика равны (1,0; -9,8) м/с. Чтобы найти величину вектора скорости (а не его отдельных компонент) в момент столкновения с поверхностью Земли, выполним следующие вычисления:
Триумфальный финал! Мячик пролетит 1,0 метра по горизонтали и столкнется с поверхностью Земли со скоростью 9,9 м/с. Совсем неплохо для начала.
Глава 4. Едем по указателям
3.8 (75%) 8 votes
- Сложение векторов.
- Умножение вектора на скаляр.
- Линейные функции.
- Умножение двух векторов.
- Скалярные произведения.
- Векторные произведения.
- Тройные произведения.
- ДИФФЕРЕНЦИРОВАНИЕ ВЕКТОРА
- Вектор и скалярные поля.
- Градиент.
- Дивергенция и ротор.
- Теорема дивергенции (теорема Остроградского – Гаусса)
- Теорема Стокса
ВЕКТОР. В физике и математике вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким, как масса, объем, давление, температура и плотность, которые можно описать обычным числом, и называются они «скалярами».
Векторная запись используется при работе с величинами, которые невозможно задать полностью с помощью обычных чисел. Например, мы хотим описать положение предмета относительно некоторой точки. Мы можем сказать, сколько километров от точки до предмета, но не можем полностью определить его местоположение, пока не узнаем направление, в котором он находится. Таким образом, местонахождение предмета характеризуется численным значением (расстоянием в километрах) и направлением.
Графически векторы изображаются в виде направленных отрезков прямой определенной длины, как на рис. 1. Например, для того чтобы представить графически силу в пять килограммов, надо нарисовать отрезок прямой длиной в пять единиц в направлении действия силы. Стрелка указывает, что сила действует от A к B; если бы сила действовала от B к A, то мы бы записали
или
. Для удобства векторы обычно обозначаются полужирными прописными буквами (A, B, C и так далее); векторы A и –A имеют равные численные значения, но противоположны по направлению. Численное значение вектора А называется модулем или длиной и обозначается A или |A|. Это величина, конечно, скаляр. Вектор, начало и конец которого совпадают, называется нулевым и обозначается O.
Два вектора называются равными (или свободными), если их модули и направления совпадают. В механике и физике этим определением, однако, надо пользоваться с осторожностью, так как две равных силы, приложенные к различным точкам тела в общем случае будут приводить к различным результатам. В связи с этим векторы подразделяются на «связанные» или «скользящие», следующим образом:
Связанные векторы имеют фиксированные точки приложения. Например, радиус-вектор указывает положение точки относительно некоторого фиксированного начала координат. Связанные векторы считаются равными, если у них совпадают не только модули и направления, но они имеют и общую точку приложения.
Скользящими векторами называются равные между собой векторы, расположенные на одной прямой.
Сложение векторов.
Идея сложения векторов возникла из того, что мы можем найти единственный вектор, который оказывает то же воздействие, что и два других вектора вместе. Если для того, чтобы попасть в некоторую точку, нам надо пройти сначала A километров в одном направлении и затем B километров в другом направлении, то мы могли бы достичь нашей конечной точки пройдя C километров в третьем направлении (рис. 2). В этом смысле можно сказать, что
A + B = C.
Вектор C называется «результирующим вектором» A и B, он задается построением, показанным на рисунке; на векторах A и B как на сторонах построен параллелограмм, а C – диагональ, соединяющая начало А и конец В. Из рис. 2 видно, что сложение векторов «коммутативно», т.е.
A + B = B + A.
Аналогичным образом можно сложить несколько векторов, последовательно соединяя их «непрерывной цепочкой», как показано на рис. 3 для трех векторов D, E и F. Из рис. 3 также видно, что
(D + E) + F = D + (E + F),
т.е. сложение векторов ассоциативно. Суммировать можно любое число векторов, причем векторы необязательно должны лежать в одной плоскости. Вычитание векторов представляется как сложение с отрицательным вектором. Например,
A – B = A + (–B),
где, как определялось ранее, –B – вектор, равный В по модулю, но противоположный по направлению.
Это правило сложения может теперь использоваться как реальный критерий проверки, является ли некоторая величина вектором или нет. Перемещения обычно подчиняются условиям этого правила; то же можно сказать и о скоростях; силы складываются таким же образом, как можно было видеть из «треугольника сил». Однако, некоторые величины, обладающие как численными значениями так и направлениями, не подчиняются этому правилу, поэтому не могут рассматриваться как векторы. Примером являются конечные вращения.
Умножение вектора на скаляр.
Произведение mA или Am, где m (m № 0) – скаляр, а A – ненулевой вектор, определяется как другой вектор, который в m раз длиннее A и имеет тоже направление что и A, если число m положительно, и противоположное, если m отрицательно, как показано на рис. 4, где m равно 2 и –1/2 соответственно. Кроме того, 1A = A, т.е. при умножении на 1 вектор не изменяется. Величина –1A – вектор, равный A по длине, но противоположный по направлению, обычно записывается как –A. Если А – нулевой вектор и(или) m = 0, то mA – нулевой вектор. Умножение дистрибутивно, т.е.
Мы можем складывать любое число векторов, причем порядок слагаемых не влияет на результат. Верно и обратное: любой вектор раскладывается на две или более «компоненты», т.е. на два вектора или более, которые, будучи сложенными, в качестве результирующего дадут исходный вектор. Например, на рис. 2, A и B – компоненты C.
Многие математические действия с векторами упрощаются, если разложить вектор на три компоненты по трем взаимно перпендикулярным направлениям. Выберем правую систему декартовых координат с осями Ox, Oy и Oz как показано на рис. 5. Под правой системой координат мы подразумеваем, что оси x, y и z располагаются так, как могут быть расположены соответственно большой, указательный и средний пальцы правой руки. Из одной правой системы координат всегда можно получить другую правую систему координат соответствующим вращением. На рис. 5, показано разложение вектор A на три компоненты и
. Они в сумме составляют вектор A, так как
Следовательно,
Можно было бы также сначала сложить и получить
, а затем к
прибавить
.
Проекции вектора А на три координатные оси, обозначенные Ax, Ay и Az называются «скалярными компонентами» вектора A:
где a, b и g – углы между A и тремя координатными осями. Теперь введем три вектора единичной длины i, j и k (орты), имеющие то же самое направление, что и соответствующие оси x, y и z. Тогда, если Ax умножить на i, то полученное произведение – это вектор, равный , и
Два вектора равны тогда и только тогда, когда равны их соответствующие скалярные компоненты. Таким образом, A = B тогда и только тогда, когда Ax = Bx, Ay = By, Az = Bz.
Два вектора можно сложить, складывая их компоненты:
Кроме того, по теореме Пифагора:
Линейные функции.
Выражение aA + bB, где a и b – скаляры, называется линейной функцией векторов A и B. Это вектор, находящийся в той же плоскости, что A и B; если A и B не параллельны, то при изменении a и b вектор aA + bB будет перемещаться по всей плоскости (рис. 6). Если A, B и C не все лежат в одной плоскости, то вектор aA + bB + cC (a, b и c изменяются) перемещается по всему пространству. Предположим, что A, B и C – единичные векторы i, j и k. Вектор ai лежит на оси x; вектор ai + bj может перемещаться по всей плоскости xy; вектор ai + bj + ck может перемещаться по всему пространству.
Можно было бы выбрать четыре взаимно перпендикулярных вектора i, j, k и l и определить четырехмерный вектор как величину
A = Axi + Ayj + Azk + Awl
с длиной
а можно было бы продолжать до пяти, шести или любого числа измерений. Хотя визуально такой вектор представить невозможно, никаких математических трудностей здесь не возникает. Такая запись часто бывает полезна; например, состояние движущейся частицы описывается шестимерным вектором P (x, y, z, px, py, pz), компоненты которого – ее положение в пространстве (x, y, z) и импульс (px, py, pz). Такое пространство называется «фазовым пространством»; если мы рассматриваем две частицы, то фазовое пространство 12-мерное, если три, то 18-ти и так далее. Число размерностей можно неограниченно увеличивать; при этом величины, с которыми мы будем иметь дело, ведут себя во многом также, как те, которые мы рассмотрим в оставшейся части этой статьи, а именно, трехмерные векторы.
Умножение двух векторов.
Правило сложения векторов было получено путем изучения поведения величин, представленных векторами. Нет никаких видимых причин, по которым два вектора нельзя было бы каким-либо образом перемножить, однако это умножение будет иметь смысл только в том случае, если можно показать его математическую состоятельность; кроме того, желательно, чтобы произведение имело определенный физический смысл.
Существуют два способа умножения векторов, которые соответствуют этим условиям. Результатом одного из них является скаляр, такое произведение называется «скалярным произведением» или «внутренним произведением» двух векторов и записывается AЧB или (A, B). Результатом другого умножения является вектор, называемый «векторным произведением» или «внешним произведением» и записывается AґB или [A, B]. Скалярные произведения имеют физический смысл для одного-, двух- или трех измерений, тогда как векторные произведения определены только для трех измерений.
Скалярные произведения.
Если под действием некоторой силы F точка, к которой она приложена, перемещается на расстояние r, то выполненная работа равна произведению r и компоненты F в направлении r. Эта компонента равна F cos бF, rс, где бF, rс – угол между F и r, т.е.
Произведенная работа = Fr cos бF, rс.
Это – пример физического обоснования скалярного произведения, определенного для любых двух векторов A, B посредством формулы
AЧB = AB cos бA, Bс.
Так как все величины правой части уравнения – скаляры, то
AЧB = BЧA;
следовательно, скалярное умножение коммутативно.
Скалярное умножение также обладает свойством дистрибутивности:
AЧ(B + С) = AЧB + AЧС.
Если векторы A и B перпендикулярны, то cos бA, Bс равен нулю, и, поэтому, AЧB = 0, даже если ни A, ни B не равны нулю. Именно поэтому мы не можем делить на вектор. Допустим, что мы разделили обе части уравнения AЧB = AЧC на A. Это дало бы B = C, и, если бы можно было бы выполнить деление, то это равенство стало бы единственным возможным результатом. Однако, если мы перепишем уравнение AЧB = AЧC в виде AЧ(B – C) = 0 и вспомним, что (B – C) – вектор, то ясно, что (B – C) необязательно равен нулю и, следовательно, B не должен быть равным C. Эти противоречивые результаты показывают, что векторное деление невозможно.
Скалярное произведение дает еще один способ записи численного значения (модуля) вектора:
AЧA = AAЧcos 0° = A2;
поэтому
Скалярное произведение можно записать и другим способом. Для этого вспомним, что:
A = Ax i + Ayj + Azk.
Заметим, что
Тогда,
Поскольку последнее уравнение содержит x, y и z в качестве нижних индексов, уравнение, казалось бы, зависит от выбранной конкретной системы координат. Однако это не так, что видно из определения, которое не зависит от выбранных координатных осей.
Векторные произведения.
Векторным или внешним произведением векторов называется вектор, модуль которого равен произведению их модулей на синус угла, перпендикулярный исходным векторам и составляющий вместе с ними правую тройку. Это произведение легче всего ввести, рассматривая соотношение между скоростью и угловой скоростью. Первая – вектор; мы теперь покажем, что последнюю также можно интерпретировать как вектор.
Угловая скорость вращающегося тела определяется следующим образом: выберем любую точку на теле и проведем перпендикуляр из этой точки до оси вращения. Тогда угловая скорость тела – это число радиан, на которые эта линия повернулась за единицу времени.
Если угловая скорость – вектор, она должна иметь численное значение и направление. Численное значение выражается в радианах в секунду, направление можно выбрать вдоль оси вращения, можно его определить, направив вектор в том направлении, в котором двигался бы правосторонний винт при вращении вместе с телом.
Рассмотрим вращение тела вокруг фиксированной оси. Если установить эту ось внутри кольца, которое в свою очередь закреплено на оси, вставленной внутрь другого кольца, мы можем придать вращение телу внутри первого кольца с угловой скоростью w1 и затем заставить внутреннее кольцо (и тело) вращаться с угловой скоростью w2. Рисунок 7 поясняет суть дела; круговые стрелки показывают направления вращения. Данное тело – это твердая сфера с центром О и радиусом r.
Придадим этому телу движение, которое является суммой двух различных угловых скоростей. Это движение довольно трудно представить наглядно, но достаточно очевидно, что тело больше не вращается относительно фиксированной оси. Однако все-таки можно сказать, что оно вращается. Чтобы показать это, выберем некоторую точку P на поверхности тела, которая в рассматриваемый нами момент времени находится на большом круге, соединяющем точки, в которых две оси пересекают поверхность сферы. Опустим перпендикуляры из P на оси. Эти перпендикуляры станут радиусами PJ и PK окружностей PQRS и PTUW соответственно. Проведем прямую POPў, проходящую через центр сферы. Теперь точка P, в рассматриваемый момент времени одновременно перемещается по окружностям, которые соприкасаются в точке P. За малый интервал времени Dt, P перемещается на расстояние
Это расстояние равно нулю, если
В этом случае точка P находится в состоянии мгновенного покоя, и точно также все точки на прямой POPў. Остальная часть сферы будет в движении (окружности, по которым перемещаются другие точки, не касаются, а пересекаются). POPў является, таким образом, мгновенной осью вращения сферы, подобно тому, как колесо, катящееся по дороге в каждый момент времени, вращается относительно своей нижней точки.
Чему равна угловая скорость сферы? Выберем для простоты точку A, в которой ось w1 пересекает поверхность. В момент времени, который мы рассматриваем, она перемещается за время Dt на расстояние
по кругу радиуса r sin w1. По определению, угловая скорость
Из этой формулы и соотношения (1) мы получим
Другими словами, если записать численное значение и выбрать направление угловой скорости так, как это описано выше, то эти величины складываются как векторы и могут быть рассмотрены как таковые.
Теперь можно ввести векторное произведение; рассмотрим тело, вращающееся с угловой скоростью w. Выберем любую точку P на теле и любое начало координат О, которое находится на оси вращения. Пусть r – вектор, направленный от О к P. Точка P движется по окружности со скоростью
V = w r sin (w, r).
Вектор скорости V является касательным к окружности и указывает в направлении, показанном на рис. 8.
Это уравнение дает зависимость скорости V точки от комбинации двух векторов w и r. Используем это соотношение, чтобы определить новый вид произведения, и запишем:
V = w ґ r.
Так как результатом такого умножения является вектор, это произведение названо векторным. Для любых двух векторов A и B, если
A ґ B = C,
то
C = AB sin бA, Bс,
и направление вектора C таково, что он перпендикулярен плоскости, проходящей через А и B и указывает в направлении, совпадающем с направлением движения правовращающегося винта, если он параллелен C и вращается от A к B. Другими словами, мы можем сказать, что A, B и C, расположенные в таком порядке, образуют правый набор координатных осей. Векторное произведение антикоммутативно; вектор B ґ A имеет тот же модуль, что и A ґ B, но направлен в противоположную сторону:
A ґ B = –B ґ A.
Это произведение дистрибутивно, но не ассоциативно; можно доказать, что
Посмотрим, как записывается векторное произведение в терминах компонент и единичных векторов. Прежде всего, для любого вектора A,
A ґ A = AA sin 0 = 0.
Следовательно, в случае единичных векторов,
i ґ i = j ґ j = k ґ k = 0
и
i ґ j = k, j ґ k = i, k ґ i = j.
Тогда,
Это равенство также можно записать в виде определителя:
Если A ґ B = 0, то либо A или B равно 0, либо A и B коллинеарны. Таким образом, как и в случае скалярного произведения, деление на вектор невозможно. Величина A ґ B равна площади параллелограмма со сторонами A и B. Это легко видеть, так как B sin бA, Bс – его высота и A – основание.
Существует много других физических величин, которые являются векторными произведениями. Одно из наиболее важных векторных произведений появляется в теории электромагнетизма и называется вектором Пойтинга P. Этот вектор задается следующим образом:
P = E ґ H,
где E и H – векторы электрического и магнитного полей соответственно. Вектор P можно рассматривать как заданный поток энергии в ваттах на квадратный метр в любой точке. Приведем еще несколько примеров: момент силы F (крутящий момент) относительно начала координат, действующей на точку, радиус-вектор которой r, определяется как r ґ F; частица, находящаяся в точке r, массой m и скоростью V, имеет угловой момент mr ґ V относительно начала координат; сила, действующая на частицу, несущую электрический заряд q через магнитное поле B со скоростью V, есть qV ґ B.
Тройные произведения.
Из трех векторов мы можем сформировать следующие тройные произведения: вектор (AЧB) ґ C; вектор (A ґ B) ґ C; скаляр (A ґ B)ЧC.
Первый тип – произведение вектора C и скаляра AЧB; о таких произведениях мы уже говорили. Второй тип называется двойным векторным произведением; вектор A ґ B перпендикулярен к плоскости, где лежат A и B, и поэтому (A ґ B) ґ C – вектор, лежащий в плоскости A и B и перпендикулярный C. Следовательно, в общем случае, (A ґ B) ґ C № A ґ (B ґ C). Записав A, B и C через их координаты (компоненты) по осям x, y и z и умножив, можно показать, что A ґ (B ґ C) = B ґ (AЧC) – C ґ (AЧB). Третий тип произведения, который возникает при расчетах решетки в физике твердого тела, численно равен объему параллелепипеда с ребрами A, B, C. Так как (A ґ B)ЧC = AЧ(B ґ C), знаки скалярного и векторного умножений можно менять местами, и произведение часто записывается как (A B C). Это произведение равно определителю
Заметим, что (A B C) = 0, если все три вектора лежат в одной и той же плоскости или, если А = 0 или (и) В = 0 или (и) С = 0.
ДИФФЕРЕНЦИРОВАНИЕ ВЕКТОРА
Предположим, что вектор U является функцией одной скалярной переменной t. Например, U может быть радиус-вектором, проведенным из начала координат до перемещающейся точки, а t – временем. Пусть t изменится на небольшую величину Dt, что приведет к изменению U на величину DU. Это показано на рис. 9. Отношение DU/Dt – вектор, направленный в том же направлении, что и DU. Мы можем определить производную U по t, как
при условии, что такой предел существует. С другой стороны, можно представить U как сумму компонент по трем осям и записать
Если U – радиус-вектор r, то dr/dt – скорость точки, выраженная как функция времени. Продифференцировав по времени еще раз, мы получим ускорение. Предположим, что точка перемещается вдоль кривой, показанной на рис. 10. Пусть s – расстояние, пройденное точкой вдоль кривой. В течение малого интервала времени Dt точка пройдет расстояние Ds вдоль кривой; положение радиус-вектора изменится на Dr. Следовательно Dr/Ds – вектор направленный как Dr. Далее
есть единичный вектор, касательный к кривой. Это видно из того, что при приближении точки Q к точке P, PQ приближается к касательной и Dr приближается к Ds.
Формулы для дифференцирования произведения подобны формулам для дифференцирования произведения скалярных функций; однако, так как векторное произведение антикоммутативно, порядок умножения должен быть сохранен. Поэтому,
Таким образом, мы видим, что, если вектор является функцией одной скалярной переменной, то мы можем представить производную почти также, как в случае скалярной функции.
Вектор и скалярные поля.
Градиент.
В физике часто приходится иметь дело с векторными или скалярными величинами, которые меняются от точки к точке в заданной области. Такие области называются «полями». Например, скаляр может быть температурой или давлением; вектор может быть скоростью движущейся жидкости или электростатическим полем системы зарядов. Если мы выбрали некоторую систему координат, то любой точке P (x, y, z) в заданной области соответствует некоторый радиус-вектор r (= xi + yj + zk) и также значение векторной величины U (r) или скаляра f (r), связанных с ним. Предположим, что U и f определены в области однозначно; т.е. каждой точке соответствует одна и только одна величина U или f, хотя различные точки могут, конечно, иметь различные значения. Допустим, что мы хотим описать скорость, с которой U и f изменяются при передвижении по этой области.
Простые частные производные, такие, как ¶U/¶x и ¶f/¶y, нас не устраивают, потому что они зависят от конкретно выбранных координатных осей. Однако можно ввести векторный дифференциальный оператор, независимый от выбора осей координат; этот оператор называется «градиентом».
Пусть мы имеем дело со скалярным полем f. Сначала в качестве примера рассмотрим контурную карту области страны. В этом случае f – высота над уровнем моря; контурные линии соединяют точки с одним и тем же значением f. При движении вдоль любой из этих линий f не меняется; если двигаться перпендикулярно этим линиям, то скорость изменения f будет максимальной. Мы можем каждой точке сопоставить вектор, указывающий величину и направление максимального изменения скорости f; такая карта и некоторые из этих векторов показаны на рис. 11. Если мы проделаем это для каждой точки поля, то получим векторное поле, связанное со скалярным полем f. Это поле вектора, называемого «градиентом» f, который записывается как grad f или Сf (символ С также называется «набла»).
В случае трех измерений, контурные линии становятся поверхностями. Малое смещение Dr (= iDx + jDy + kDz) приводит к изменению f, которое записывается как
где точками обозначены члены более высоких порядков. Это выражение можно записать в виде скалярного произведения
Разделим правую и левую части этого равенства на Ds, и пусть Ds стремится к нулю; тогда
где dr/ds – единичный вектор в выбранном направлении. Выражение в круглых скобках – вектор, зависящий от выбранной точки. Таким образом, df/ds имеет максимальное значение, когда dr/ds указывает в том же направлении, выражение, стоящее в скобках, является градиентом. Таким образом,
– вектор, равный по величине и совпадающий по направлению с максимальной скоростью изменения f относительно координат. Градиент f часто записывается в виде
Это означает, что оператор С существует сам по себе. Во многих случаях он ведет себя, как вектор, и фактически является «векторным дифференциальным оператором» – одним из наиболее важных дифференциальных операторов в физике. Несмотря на то, что С содержит единичные векторы i, j и k, его физический смысл не зависит от выбранной системы координат.
Какова связь между Сf и f? Прежде всего предположим, что f определяет потенциал в любой точке. При любом малом смещении Dr величина f изменится на
Если q – величина (например масса, заряд), перемещенная на Dr, то работа, выполненная при перемещении q на Dr равна
Так как Dr – перемещение, то qСf – сила; –Сf – напряженность (сила на единицу количества), связанная с f. Например, пусть U – электростатический потенциал; тогда E – напряженность электрического поля, задается формулой
E = –СU.
Допустим, что U создается точечным электрическим зарядом в q кулонов, помещенным в начало координат. Значение U в точке P (x, y, z) с радиус-вектором r задается формулой
где e0 – диэлектрическая постоянная свободного пространства. Поэтому
откуда следует, что E действует в направлении r и его величина равна q/(4pe0r3).
Зная скалярное поле, можно определить связанное с ним векторное поле. Также возможно и обратное. С точки зрения математической обработки скалярными полями оперировать легче, чем векторными, так как они задаются одной функцией координат, в то время как векторное поле требует три функции, соответствующие компонентам вектора в трех направлениях. Таким образом, возникает вопрос: дано векторное поле, может ли мы записать связанное с ним скалярное поле?
Дивергенция и ротор.
Мы видели результат действия С на скалярную функцию. Что произойдет, если С применить к вектору? Имеются две возможности: пусть U (x, y, z) – вектор; тогда мы можем образовать векторное и скалярное произведения следующим образом:
Первое из этих выражений – скаляр, называемый дивергенцией U (обозначается divU); второе – вектор, названный ротор U (обозначается rotU).
Эти дифференциальные функции, дивергенция и ротор, широко используются в математической физике.
Представьте, что U – некоторый вектор и что он и его первые производные непрерывны в некоторой области. Пусть P – точка в этой области, окруженная малой замкнутой поверхностью S, ограничивающей объем DV. Пусть n – единичный вектор, перпендикулярный к этой поверхности в каждой точке (n меняет направление при движении вокруг поверхности, но всегда имеет единичную длину); пусть n направлен наружу. Покажем, что
и
Здесь S указывает, что эти интегралы берутся по всей поверхности, da – элемент поверхности S.
Для простоты мы выберем удобную для нас форму S в виде небольшого параллелепипеда (как показано на рис. 12) со сторонами Dx, Dy и Dz; точка P – центр параллелепипеда. Вычислим интеграл из уравнения (4) сначала по одной грани параллелепипеда. Для передней грани n = i (единичный вектор параллелен оси x); Da = DyDz. Вклад в интеграл от передней грани равен
На противоположной грани n = –i; эта грань дает вклад в интеграл
Используя теорему Тейлора, получим общий вклад от двух граней
Заметим, что DxDyDz = DV. Аналогичным образом можно вычислить вклад от двух других пар граней. Полный интеграл равен
и если мы положим DV ® 0, то члены более высокого порядка исчезнут. По формуле (2) выражение в скобках – это divU, что доказывает равенство (4).
Равенство (5) можно доказать таким же образом. Воспользуемся снова рис. 12; тогда вклад от передней грани в интеграл будет равен
и, используя теорему Тейлора, получим, что суммарный вклад в интеграл от двух граней имеет вид
т.е. это два члена из выражения для rotU в уравнении (3). Другие четыре члена получатся после учета вкладов от других четырех граней.
Что, в сущности, означают эти соотношения? Рассмотрим равенство (4). Предположим, что U – скорость (жидкости, например). Тогда nЧU da = Un da, где Unявляется нормальной компонентой вектора U к поверхности. Поэтому, Un da – это объем жидкости, протекающей через da в единицу времени, а – это объем жидкости, вытекающей через S в единицу времени. Следовательно,
– скорость расширения единицы объема вокруг точки P. Отсюда дивергенция получила свое название; она показывает скорость, с которой жидкость расширяется из (т.е. расходится от) P.
Чтобы объяснить физическое значение ротора U, рассмотрим другой поверхностный интеграл по маленькому цилиндрическому объему высотой h, окружающему точку P; плоско-параллельные поверхности могут быть ориентированы в любом направлении, которое мы выбираем. Пусть k –единичный вектор перпендикулярный к каждой поверхности, и пусть площадь каждой поверхности DA; тогда полный объем DV = hDA (рис. 13). Рассмотрим теперь интеграл
Подынтегральное выражение – уже упоминавшееся ранее тройное скалярное произведение. Это произведение будет равно нулю на плоских поверхностях, где k и n параллельны. На кривой поверхности
где ds – элемент кривой как показано на рис. 13. Сравнивая эти равенства с соотношением (5), получаем, что
Мы по-прежнему предполагаем, что U – скорость. Чему в таком случае будет равна средняя угловая скорость жидкости вокруг k? Очевидно, что
если DA ® 0. Это выражение максимально, когда k и rotU указывают в одном и том же направлении; это означает, что rotU – вектор, равный удвоенной угловой скорости жидкости в точке P. Если жидкость вращается относительно P, то rotU № 0, и векторы U будут вращаться вокруг P. Отсюда и возникло название ротора.
Теорема дивергенции (теорема Остроградского – Гаусса)
Теорема дивергенции (теорема Остроградского – Гаусса) является обобщением формулы (4) для конечных объемов. Она утверждает, что для некоторого объема V, ограниченного замкнутой поверхностью S,
и справедлива для всех непрерывных векторных функций U, имеющих непрерывные первые производные всюду в V и на S. Мы не будем приводить здесь доказательство этой теоремы, но ее справедливость можно понять интуитивно, представляя объем V разделенным на ячейки. Поток U через поверхность, общую для двух ячеек обращается в нуль, и только ячейки, находящиеся на границе S внесут вклад в поверхностный интеграл.
Теорема Стокса
является обобщением уравнения (6) для конечных поверхностей. Она утверждает, что
где C – замкнутая кривая и S – любая поверхность, ограниченная этой кривой. U и ее первые производные должны быть непрерывны всюду на S и C.

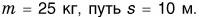
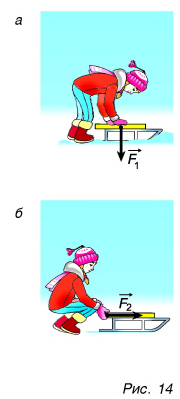
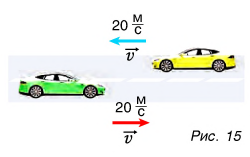
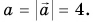
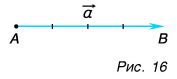
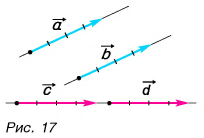
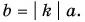
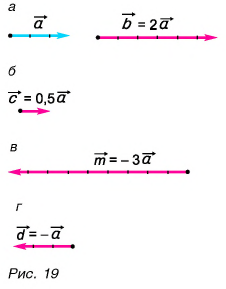
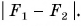

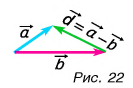
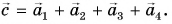
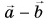 можно найти как сумму
можно найти как сумму 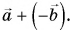
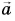 на число
на число 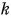 есть вектор
есть вектор 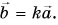 При
При 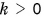 направления векторов
направления векторов 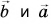 совпадают, а при
совпадают, а при 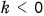 — противоположны. Модуль вектора
— противоположны. Модуль вектора 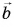 равен
равен 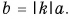

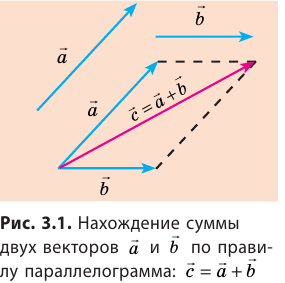
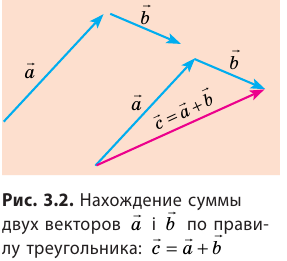
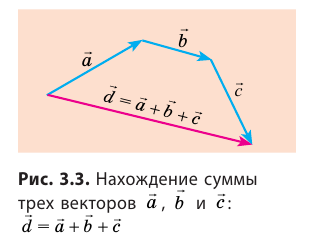
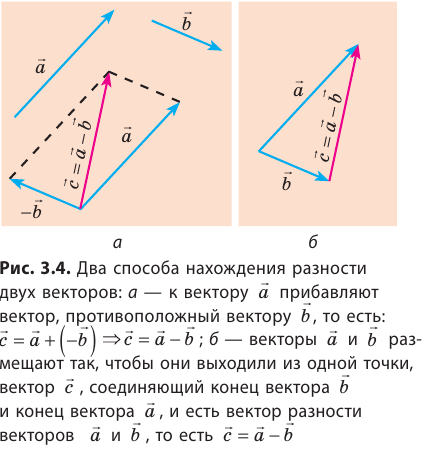
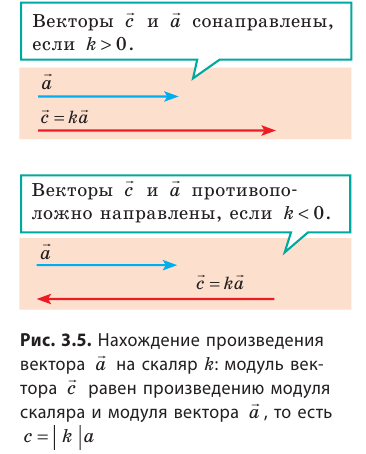
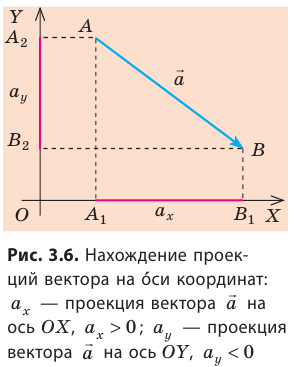
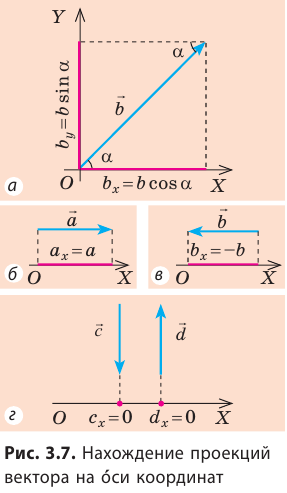
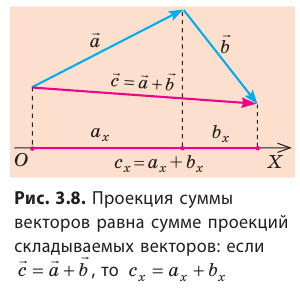










![{displaystyle mathbf {a} ={begin{bmatrix}a_{1}\a_{2}\a_{3}\end{bmatrix}}=[a_{1} a_{2} a_{3}]^{operatorname {T} }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a4d592431150c7ec8a51217d87dae2ed1224df2)