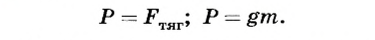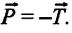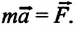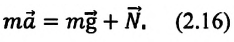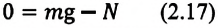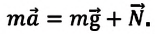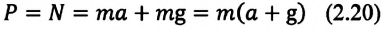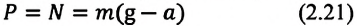This page is about the physical concept. In law, commerce, and in colloquial usage weight may also refer to mass. For other uses see weight (disambiguation).
| Weight | |
|---|---|

A spring scale measures the weight of an object. |
|
|
Common symbols |
 |
| SI unit | newton (N) |
|
Other units |
pound-force (lbf) |
| In SI base units | kg⋅m⋅s−2 |
| Extensive? | Yes |
| Intensive? | No |
| Conserved? | No |
|
Derivations from |
|
| Dimension |  |
In science and engineering, the weight of an object is the force acting on the object due to gravity.[1][2][3]
Some standard textbooks[4] define weight as a vector quantity, the gravitational force acting on the object. Others[5][6] define weight as a scalar quantity, the magnitude of the gravitational force. Yet others[7] define it as the magnitude of the reaction force exerted on a body by mechanisms that counteract the effects of gravity: the weight is the quantity that is measured by, for example, a spring scale. Thus, in a state of free fall, the weight would be zero. In this sense of weight, terrestrial objects can be weightless: ignoring air resistance, the famous apple falling from the tree, on its way to meet the ground near Isaac Newton, would be weightless.
The unit of measurement for weight is that of force, which in the International System of Units (SI) is the newton. For example, an object with a mass of one kilogram has a weight of about 9.8 newtons on the surface of the Earth, and about one-sixth as much on the Moon. Although weight and mass are scientifically distinct quantities, the terms are often confused with each other in everyday use (e.g. comparing and converting force weight in pounds to mass in kilograms and vice versa).[8]
Further complications in elucidating the various concepts of weight have to do with the theory of relativity according to which gravity is modeled as a consequence of the curvature of spacetime. In the teaching community, a considerable debate has existed for over half a century on how to define weight for their students. The current situation is that a multiple set of concepts co-exist and find use in their various contexts.[2]
History[edit]
Weighing grain, from the Babur-namah[9]
Discussion of the concepts of heaviness (weight) and lightness (levity) date back to the ancient Greek philosophers. These were typically viewed as inherent properties of objects. Plato described weight as the natural tendency of objects to seek their kin. To Aristotle, weight and levity represented the tendency to restore the natural order of the basic elements: air, earth, fire and water. He ascribed absolute weight to earth and absolute levity to fire. Archimedes saw weight as a quality opposed to buoyancy, with the conflict between the two determining if an object sinks or floats. The first operational definition of weight was given by Euclid, who defined weight as: «the heaviness or lightness of one thing, compared to another, as measured by a balance.»[2] Operational balances (rather than definitions) had, however, been around much longer.[10]
According to Aristotle, weight was the direct cause of the falling motion of an object, the speed of the falling object was supposed to be directly proportionate to the weight of the object. As medieval scholars discovered that in practice the speed of a falling object increased with time, this prompted a change to the concept of weight to maintain this cause-effect relationship. Weight was split into a «still weight» or pondus, which remained constant, and the actual gravity or gravitas, which changed as the object fell. The concept of gravitas was eventually replaced by Jean Buridan’s impetus, a precursor to momentum.[2]
The rise of the Copernican view of the world led to the resurgence of the Platonic idea that like objects attract but in the context of heavenly bodies. In the 17th century, Galileo made significant advances in the concept of weight. He proposed a way to measure the difference between the weight of a moving object and an object at rest. Ultimately, he concluded weight was proportionate to the amount of matter of an object, not the speed of motion as supposed by the Aristotelean view of physics.[2]
Newton[edit]
The introduction of Newton’s laws of motion and the development of Newton’s law of universal gravitation led to considerable further development of the concept of weight. Weight became fundamentally separate from mass. Mass was identified as a fundamental property of objects connected to their inertia, while weight became identified with the force of gravity on an object and therefore dependent on the context of the object. In particular, Newton considered weight to be relative to another object causing the gravitational pull, e.g. the weight of the Earth towards the Sun.[2]
Newton considered time and space to be absolute. This allowed him to consider concepts as true position and true velocity.[clarification needed] Newton also recognized that weight as measured by the action of weighing was affected by environmental factors such as buoyancy. He considered this a false weight induced by imperfect measurement conditions, for which he introduced the term apparent weight as compared to the true weight defined by gravity.[2]
Although Newtonian physics made a clear distinction between weight and mass, the term weight continued to be commonly used when people meant mass. This led the 3rd General Conference on Weights and Measures (CGPM) of 1901 to officially declare «The word weight denotes a quantity of the same nature as a force: the weight of a body is the product of its mass and the acceleration due to gravity», thus distinguishing it from mass for official usage.
Relativity[edit]
In the 20th century, the Newtonian concepts of absolute time and space were challenged by relativity. Einstein’s equivalence principle put all observers, moving or accelerating, on the same footing. This led to an ambiguity as to what exactly is meant by the force of gravity and weight. A scale in an accelerating elevator cannot be distinguished from a scale in a gravitational field. Gravitational force and weight thereby became essentially frame-dependent quantities. This prompted the abandonment of the concept as superfluous in the fundamental sciences such as physics and chemistry. Nonetheless, the concept remained important in the teaching of physics. The ambiguities introduced by relativity led, starting in the 1960s, to considerable debate in the teaching community as how to define weight for their students, choosing between a nominal definition of weight as the force due to gravity or an operational definition defined by the act of weighing.[2]
Definitions[edit]
This top-fuel dragster can accelerate from zero to 160 kilometres per hour (99 mph) in 0.86 seconds. This is a horizontal acceleration of 5.3 g. Combined with the vertical g-force in the stationary case the Pythagorean theorem yields a g-force of 5.4 g. It is this g-force that causes the driver’s weight if one uses the operational definition. If one uses the gravitational definition, the driver’s weight is unchanged by the motion of the car.
Several definitions exist for weight, not all of which are equivalent.[3][11][12][13]
Gravitational definition[edit]
The most common definition of weight found in introductory physics textbooks defines weight as the force exerted on a body by gravity.[1][13] This is often expressed in the formula W = mg, where W is the weight, m the mass of the object, and g gravitational acceleration.
In 1901, the 3rd General Conference on Weights and Measures (CGPM) established this as their official definition of weight:
«The word weight denotes a quantity of the same nature[Note 1] as a force: the weight of a body is the product of its mass and the acceleration due to gravity.»
— Resolution 2 of the 3rd General Conference on Weights and Measures[15][16]
This resolution defines weight as a vector, since force is a vector quantity. However, some textbooks also take weight to be a scalar by defining:
«The weight W of a body is equal to the magnitude Fg of the gravitational force on the body.»[17]
The gravitational acceleration varies from place to place. Sometimes, it is simply taken to have a standard value of 9.80665 m/s2, which gives the standard weight.[15]
The force whose magnitude is equal to mg newtons is also known as the m kilogram weight (which term is abbreviated to kg-wt)[18]
Left: A spring scale measures weight, by seeing how much the object pushes on a spring (inside the device). On the Moon, an object would give a lower reading. Right: A balance scale indirectly measures mass, by comparing an object to references. On the Moon, an object would give the same reading, because the object and references would both become lighter.
Operational definition[edit]
In the operational definition, the weight of an object is the force measured by the operation of weighing it, which is the force it exerts on its support.[11] Since W is the downward force on the body by the centre of earth and there is no acceleration in the body, there exists an opposite and equal force by the support on the body. Also it is equal to the force exerted by the body on its support because action and reaction have same numerical value and opposite direction. This can make a considerable difference, depending on the details; for example, an object in free fall exerts little if any force on its support, a situation that is commonly referred to as weightlessness. However, being in free fall does not affect the weight according to the gravitational definition. Therefore, the operational definition is sometimes refined by requiring that the object be at rest.[citation needed] However, this raises the issue of defining «at rest» (usually being at rest with respect to the Earth is implied by using standard gravity).[citation needed] In the operational definition, the weight of an object at rest on the surface of the Earth is lessened by the effect of the centrifugal force from the Earth’s rotation.
The operational definition, as usually given, does not explicitly exclude the effects of buoyancy, which reduces the measured weight of an object when it is immersed in a fluid such as air or water. As a result, a floating balloon or an object floating in water might be said to have zero weight.
ISO definition[edit]
In the ISO International standard ISO 80000-4:2006,[19] describing the basic physical quantities and units in mechanics as a part of the International standard ISO/IEC 80000, the definition of weight is given as:
Definition
,
- where m is mass and g is local acceleration of free fall.
Remarks
- When the reference frame is Earth, this quantity comprises not only the local gravitational force, but also the local centrifugal force due to the rotation of the Earth, a force which varies with latitude.
- The effect of atmospheric buoyancy is excluded in the weight.
- In common parlance, the name «weight» continues to be used where «mass» is meant, but this practice is deprecated.
— ISO 80000-4 (2006)
The definition is dependent on the chosen frame of reference. When the chosen frame is co-moving with the object in question then this definition precisely agrees with the operational definition.[12] If the specified frame is the surface of the Earth, the weight according to the ISO and gravitational definitions differ only by the centrifugal effects due to the rotation of the Earth.
Apparent weight[edit]
In many real world situations the act of weighing may produce a result that differs from the ideal value provided by the definition used. This is usually referred to as the apparent weight of the object. A common example of this is the effect of buoyancy, when an object is immersed in a fluid the displacement of the fluid will cause an upward force on the object, making it appear lighter when weighed on a scale.[20] The apparent weight may be similarly affected by levitation and mechanical suspension. When the gravitational definition of weight is used, the operational weight measured by an accelerating scale is often also referred to as the apparent weight.[21]
Mass[edit]
An object with mass m resting on a surface and the corresponding free body diagram of just the object showing the forces acting on it. Notice that the amount of force that the table is pushing upward on the object (the N vector) is equal to the downward force of the object’s weight (shown here as mg, as weight is equal to the object’s mass multiplied with the acceleration due to gravity): because these forces are equal, the object is in a state of equilibrium (all the forces and moments acting on it sum to zero).
In modern scientific usage, weight and mass are fundamentally different quantities: mass is an intrinsic property of matter, whereas weight is a force that results from the action of gravity on matter: it measures how strongly the force of gravity pulls on that matter. However, in most practical everyday situations the word «weight» is used when, strictly, «mass» is meant.[8][22] For example, most people would say that an object «weighs one kilogram», even though the kilogram is a unit of mass.
The distinction between mass and weight is unimportant for many practical purposes because the strength of gravity does not vary too much on the surface of the Earth. In a uniform gravitational field, the gravitational force exerted on an object (its weight) is directly proportional to its mass. For example, object A weighs 10 times as much as object B, so therefore the mass of object A is 10 times greater than that of object B. This means that an object’s mass can be measured indirectly by its weight, and so, for everyday purposes, weighing (using a weighing scale) is an entirely acceptable way of measuring mass. Similarly, a balance measures mass indirectly by comparing the weight of the measured item to that of an object(s) of known mass. Since the measured item and the comparison mass are in virtually the same location, so experiencing the same gravitational field, the effect of varying gravity does not affect the comparison or the resulting measurement.
The Earth’s gravitational field is not uniform but can vary by as much as 0.5%[23] at different locations on Earth (see Earth’s gravity). These variations alter the relationship between weight and mass, and must be taken into account in high-precision weight measurements that are intended to indirectly measure mass. Spring scales, which measure local weight, must be calibrated at the location at which the objects will be used to show this standard weight, to be legal for commerce.[citation needed]
This table shows the variation of acceleration due to gravity (and hence the variation of weight) at various locations on the Earth’s surface.[24]
| Location | Latitude | m/s2 | Absolute difference from equator | Percentage difference from equator |
|---|---|---|---|---|
| Equator | 0° | 9.7803 | 0.0000 | 0% |
| Sydney | 33°52′ S | 9.7968 | 0.0165 | 0.17% |
| Aberdeen | 57°9′ N | 9.8168 | 0.0365 | 0.37% |
| North Pole | 90° N | 9.8322 | 0.0519 | 0.53% |
The historical use of «weight» for «mass» also persists in some scientific terminology – for example, the chemical terms «atomic weight», «molecular weight», and «formula weight», can still be found rather than the preferred «atomic mass», etc.
In a different gravitational field, for example, on the surface of the Moon, an object can have a significantly different weight than on Earth. The gravity on the surface of the Moon is only about one-sixth as strong as on the surface of the Earth. A one-kilogram mass is still a one-kilogram mass (as mass is an intrinsic property of the object) but the downward force due to gravity, and therefore its weight, is only one-sixth of what the object would have on Earth. So a man of mass 180 pounds weighs only about 30 pounds-force when visiting the Moon.
SI units[edit]
In most modern scientific work, physical quantities are measured in SI units. The SI unit of weight is the same as that of force: the newton (N) – a derived unit which can also be expressed in SI base units as kg⋅m/s2 (kilograms times metres per second squared).[22]
In commercial and everyday use, the term «weight» is usually used to mean mass, and the verb «to weigh» means «to determine the mass of» or «to have a mass of». Used in this sense, the proper SI unit is the kilogram (kg).[22]
As of 20 May 2019, the kilogram, which is essential to evaluate the weight of an object, has been redefined in terms of Planck’s constant. The new definition does not affect the actual amount of the material but increases the measurement’s quality and decreases the uncertainty associated with it.[25]
Prior to using Planck’s constant, a physical object was used as a standard. The object, located in a vault in Sèvres, France, has fluctuated by approximately 50 micrograms of its mass since it was first introduced in 1889.[26] Consequently, the following must be true. Mass, which should be the same whether on earth or the moon for example, is only valid on earth since it needs to be referenced. Also, comparing a weight measurement to a standard that changes with time cannot be used as a reference without citing the actual value of it at the time and moment it was used as such. Therefore, to redefine the kilogram all National Metrology Institutes (NMIs) involved determined the new value of Planck’s constant by evaluating a mass which was calibrated against the IPK.[27] To this extent one kilogram is equal to h/(6.62607015×10^(-34) ) m^(-2) s which equals 1 m^(-2) s.
A kilogram has remained the same quantity it was before the redefinition.[27] But as of May 2019, the weights measured and recorded can be traced back and used as comparison for current and future work.
Pound and other non-SI units[edit]
In United States customary units, the pound can be either a unit of force or a unit of mass.[28] Related units used in some distinct, separate subsystems of units include the poundal and the slug. The poundal is defined as the force necessary to accelerate an object of one-pound mass at 1 ft/s2, and is equivalent to about 1/32.2 of a pound-force. The slug is defined as the amount of mass that accelerates at 1 ft/s2 when one pound-force is exerted on it, and is equivalent to about 32.2 pounds (mass).
The kilogram-force is a non-SI unit of force, defined as the force exerted by a one-kilogram mass in standard Earth gravity (equal to 9.80665 newtons exactly). The dyne is the cgs unit of force and is not a part of SI, while weights measured in the cgs unit of mass, the gram, remain a part of SI.
Sensation[edit]
The sensation of weight is caused by the force exerted by fluids in the vestibular system, a three-dimensional set of tubes in the inner ear.[dubious – discuss] It is actually the sensation of g-force, regardless of whether this is due to being stationary in the presence of gravity, or, if the person is in motion, the result of any other forces acting on the body such as in the case of acceleration or deceleration of a lift, or centrifugal forces when turning sharply.
Measuring[edit]
Weight is commonly measured using one of two methods. A spring scale or hydraulic or pneumatic scale measures local weight, the local force of gravity on the object (strictly apparent weight force). Since the local force of gravity can vary by up to 0.5% at different locations, spring scales will measure slightly different weights for the same object (the same mass) at different locations. To standardize weights, scales are always calibrated to read the weight an object would have at a nominal standard gravity of 9.80665 m/s2 (approx. 32.174 ft/s2). However, this calibration is done at the factory. When the scale is moved to another location on Earth, the force of gravity will be different, causing a slight error. So to be highly accurate and legal for commerce, spring scales must be re-calibrated at the location at which they will be used.
A balance on the other hand, compares the weight of an unknown object in one scale pan to the weight of standard masses in the other, using a lever mechanism – a lever-balance. The standard masses are often referred to, non-technically, as «weights». Since any variations in gravity will act equally on the unknown and the known weights, a lever-balance will indicate the same value at any location on Earth. Therefore, balance «weights» are usually calibrated and marked in mass units, so the lever-balance measures mass by comparing the Earth’s attraction on the unknown object and standard masses in the scale pans. In the absence of a gravitational field, away from planetary bodies (e.g. space), a lever-balance would not work, but on the Moon, for example, it would give the same reading as on Earth. Some balances are marked in weight units, but since the weights are calibrated at the factory for standard gravity, the balance will measure standard weight, i.e. what the object would weigh at standard gravity, not the actual local force of gravity on the object.
If the actual force of gravity on the object is needed, this can be calculated by multiplying the mass measured by the balance by the acceleration due to gravity – either standard gravity (for everyday work) or the precise local gravity (for precision work). Tables of the gravitational acceleration at different locations can be found on the web.
Gross weight is a term that is generally found in commerce or trade applications, and refers to the total weight of a product and its packaging. Conversely, net weight refers to the weight of the product alone, discounting the weight of its container or packaging; and tare weight is the weight of the packaging alone.
Relative weights on the Earth and other celestial bodies[edit]
The table below shows comparative gravitational accelerations at the surface of the Sun, the Earth’s moon, each of the planets in the solar system. The “surface” is taken to mean the cloud tops of the gas giants (Jupiter, Saturn, Uranus and Neptune). For the Sun, the surface is taken to mean the photosphere. The values in the table have not been de-rated for the centrifugal effect of planet rotation (and cloud-top wind speeds for the gas giants) and therefore, generally speaking, are similar to the actual gravity that would be experienced near the poles.
| Body | Multiple of Earth gravity |
Surface gravity m/s2 |
|---|---|---|
| Sun | 27.90 | 274.1 |
| Mercury | 0.3770 | 3.703 |
| Venus | 0.9032 | 8.872 |
| Earth | 1 (by definition) | 9.8226[29] |
| Moon | 0.1655 | 1.625 |
| Mars | 0.3895 | 3.728 |
| Jupiter | 2.640 | 25.93 |
| Saturn | 1.139 | 11.19 |
| Uranus | 0.917 | 9.01 |
| Neptune | 1.148 | 11.28 |
See also[edit]
- Human body weight – Person’s mass or weight
- Tare weight
- weight – Unit of weight the English unit
Notes[edit]
- ^ The phrase «quantity of the same nature» is a literal translation of the French phrase grandeur de la même nature. Although this is an authorized translation, VIM 3 of the International Bureau of Weights and Measures recommends translating grandeurs de même nature as quantities of the same kind.[14]
References[edit]
- ^ a b Richard C. Morrison (1999). «Weight and gravity — the need for consistent definitions». The Physics Teacher. 37 (1): 51. Bibcode:1999PhTea..37…51M. doi:10.1119/1.880152.
- ^ a b c d e f g h Igal Galili (2001). «Weight versus gravitational force: historical and educational perspectives». International Journal of Science Education. 23 (10): 1073. Bibcode:2001IJSEd..23.1073G. doi:10.1080/09500690110038585. S2CID 11110675.
- ^ a b Gat, Uri (1988). «The weight of mass and the mess of weight». In Richard Alan Strehlow (ed.). Standardization of Technical Terminology: Principles and Practice – second volume. ASTM International. pp. 45–48. ISBN 978-0-8031-1183-7.
- ^ Knight, Randall D. (2004). Physics for Scientists and Engineers: a Strategic Approach. San Francisco, USA: Addison–Wesley. pp. 100–101. ISBN 0-8053-8960-1.
- ^ Bauer, Wolfgang and Westfall, Gary D. (2011). University Physics with Modern Physics. New York: McGraw Hill. p. 103. ISBN 978-0-07-336794-1.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Serway, Raymond A. and Jewett, John W. Jr. (2008). Physics for Scientists and Engineers with Modern Physics. USA: Thompson. p. 106. ISBN 978-0-495-11245-7.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Hewitt, Paul G. (2001). Conceptual Physics. USA: Addison–Wesley. pp. 159. ISBN 0-321-05202-1.
- ^ a b The National Standard of Canada, CAN/CSA-Z234.1-89 Canadian Metric Practice Guide, January 1989:
- 5.7.3 Considerable confusion exists in the use of the term «weight». In commercial and everyday use, the term «weight» nearly always means mass. In science and technology «weight» has primarily meant a force due to gravity. In scientific and technical work, the term «weight» should be replaced by the term «mass» or «force», depending on the application.
- 5.7.4 The use of the verb «to weigh» meaning «to determine the mass of», e.g., «I weighed this object and determined its mass to be 5 kg,» is correct.
- ^ Sur Das (1590s). «Weighing Grain». Baburnama.
- ^ http://www.averyweigh-tronix.com/museum Archived 2013-02-28 at the Wayback Machine accessed 29 March 2013.
- ^ a b Allen L. King (1963). «Weight and weightlessness». American Journal of Physics. 30 (5): 387. Bibcode:1962AmJPh..30..387K. doi:10.1119/1.1942032.
- ^ a b A. P. French (1995). «On weightlessness». American Journal of Physics. 63 (2): 105–106. Bibcode:1995AmJPh..63..105F. doi:10.1119/1.17990.
- ^ a b Galili, I.; Lehavi, Y. (2003). «The importance of weightlessness and tides in teaching gravitation» (PDF). American Journal of Physics. 71 (11): 1127–1135. Bibcode:2003AmJPh..71.1127G. doi:10.1119/1.1607336.
- ^ Working Group 2 of the Joint Committee for Guides in Metrology (JCGM/WG 2) (2008). International vocabulary of metrology – Basic and general concepts and associated terms (VIM) – Vocabulaire international de métrologie – Concepts fondamentaux et généraux et termes associés (VIM) (PDF) (JCGM 200:2008) (in English and French) (3rd ed.). BIPM. Note 3 to Section 1.2.
- ^ a b «Resolution of the 3rd meeting of the CGPM (1901)». BIPM.
- ^ David B. Newell; Eite Tiesinga, eds. (2019). The International System of Units (SI) (PDF) (NIST Special publication 330, 2019 ed.). Gaithersburg, MD: NIST. p. 46.
- ^ Halliday, David; Resnick, Robert; Walker, Jearl (2007). Fundamentals of Physics. Vol. 1 (8th ed.). Wiley. p. 95. ISBN 978-0-470-04473-5.
- ^ Chester, W. Mechanics. George Allen & Unwin. London. 1979. ISBN 0-04-510059-4. Section 3.2 at page 83.
- ^ ISO 80000-4:2006, Quantities and units — Part 4: Mechanics
- ^ Bell, F. (1998). Principles of mechanics and biomechanics. Stanley Thornes Ltd. pp. 174–176. ISBN 978-0-7487-3332-3.
- ^ Galili, Igal (1993). «Weight and gravity: teachers’ ambiguity and students’ confusion about the concepts». International Journal of Science Education. 15 (2): 149–162. Bibcode:1993IJSEd..15..149G. doi:10.1080/0950069930150204.
- ^ a b c A. Thompson & B. N. Taylor (March 3, 2010) [July 2, 2009]. «The NIST Guide for the use of the International System of Units, Section 8: Comments on Some Quantities and Their Units». Special Publication 811. NIST. Retrieved 2010-05-22.
- ^ Hodgeman, Charles, ed. (1961). Handbook of Chemistry and Physics (44th ed.). Cleveland, USA: Chemical Rubber Publishing Co. pp. 3480–3485.
- ^ Clark, John B (1964). Physical and Mathematical Tables. Oliver and Boyd.
- ^ Yadav, S., & Aswal, D. K. (2020, February 25). Redefined SI Units and Their Implications. Mapan, pp. 1-9.
- ^ Jeffrey-Wilensky, J. (2019, May 20). The definition of the kilogram just changed. Here’s what that means. Retrieved from NBC News: https://www.nbcnews.com/mach/science/definition-kilogram-just-changed-here-s-what-means-ncna1007731
- ^ a b Ehtesham, B., John, T., Yadav, S., Singh, H. K., Mandal, G., & Singh, N. (2020). Journey of Kilogram from Physical Constant to Universal Physical Constant (h) via Artefact: A Brief Review. MAPAN — Journal of Metrology Society of India, 1-9
- ^ «Common Conversion Factors, Approximate Conversions from U.S. Customary Measures to Metric». Nist. National Institute of Standards and Technology. 13 January 2010. Retrieved 2013-09-03.
- ^ This value excludes the adjustment for centrifugal force due to Earth’s rotation and is therefore greater than the 9.80665 m/s2 value of standard gravity.
This page is about the physical concept. In law, commerce, and in colloquial usage weight may also refer to mass. For other uses see weight (disambiguation).
| Weight | |
|---|---|

A spring scale measures the weight of an object. |
|
|
Common symbols |
 |
| SI unit | newton (N) |
|
Other units |
pound-force (lbf) |
| In SI base units | kg⋅m⋅s−2 |
| Extensive? | Yes |
| Intensive? | No |
| Conserved? | No |
|
Derivations from |
|
| Dimension |  |
In science and engineering, the weight of an object is the force acting on the object due to gravity.[1][2][3]
Some standard textbooks[4] define weight as a vector quantity, the gravitational force acting on the object. Others[5][6] define weight as a scalar quantity, the magnitude of the gravitational force. Yet others[7] define it as the magnitude of the reaction force exerted on a body by mechanisms that counteract the effects of gravity: the weight is the quantity that is measured by, for example, a spring scale. Thus, in a state of free fall, the weight would be zero. In this sense of weight, terrestrial objects can be weightless: ignoring air resistance, the famous apple falling from the tree, on its way to meet the ground near Isaac Newton, would be weightless.
The unit of measurement for weight is that of force, which in the International System of Units (SI) is the newton. For example, an object with a mass of one kilogram has a weight of about 9.8 newtons on the surface of the Earth, and about one-sixth as much on the Moon. Although weight and mass are scientifically distinct quantities, the terms are often confused with each other in everyday use (e.g. comparing and converting force weight in pounds to mass in kilograms and vice versa).[8]
Further complications in elucidating the various concepts of weight have to do with the theory of relativity according to which gravity is modeled as a consequence of the curvature of spacetime. In the teaching community, a considerable debate has existed for over half a century on how to define weight for their students. The current situation is that a multiple set of concepts co-exist and find use in their various contexts.[2]
History[edit]
Weighing grain, from the Babur-namah[9]
Discussion of the concepts of heaviness (weight) and lightness (levity) date back to the ancient Greek philosophers. These were typically viewed as inherent properties of objects. Plato described weight as the natural tendency of objects to seek their kin. To Aristotle, weight and levity represented the tendency to restore the natural order of the basic elements: air, earth, fire and water. He ascribed absolute weight to earth and absolute levity to fire. Archimedes saw weight as a quality opposed to buoyancy, with the conflict between the two determining if an object sinks or floats. The first operational definition of weight was given by Euclid, who defined weight as: «the heaviness or lightness of one thing, compared to another, as measured by a balance.»[2] Operational balances (rather than definitions) had, however, been around much longer.[10]
According to Aristotle, weight was the direct cause of the falling motion of an object, the speed of the falling object was supposed to be directly proportionate to the weight of the object. As medieval scholars discovered that in practice the speed of a falling object increased with time, this prompted a change to the concept of weight to maintain this cause-effect relationship. Weight was split into a «still weight» or pondus, which remained constant, and the actual gravity or gravitas, which changed as the object fell. The concept of gravitas was eventually replaced by Jean Buridan’s impetus, a precursor to momentum.[2]
The rise of the Copernican view of the world led to the resurgence of the Platonic idea that like objects attract but in the context of heavenly bodies. In the 17th century, Galileo made significant advances in the concept of weight. He proposed a way to measure the difference between the weight of a moving object and an object at rest. Ultimately, he concluded weight was proportionate to the amount of matter of an object, not the speed of motion as supposed by the Aristotelean view of physics.[2]
Newton[edit]
The introduction of Newton’s laws of motion and the development of Newton’s law of universal gravitation led to considerable further development of the concept of weight. Weight became fundamentally separate from mass. Mass was identified as a fundamental property of objects connected to their inertia, while weight became identified with the force of gravity on an object and therefore dependent on the context of the object. In particular, Newton considered weight to be relative to another object causing the gravitational pull, e.g. the weight of the Earth towards the Sun.[2]
Newton considered time and space to be absolute. This allowed him to consider concepts as true position and true velocity.[clarification needed] Newton also recognized that weight as measured by the action of weighing was affected by environmental factors such as buoyancy. He considered this a false weight induced by imperfect measurement conditions, for which he introduced the term apparent weight as compared to the true weight defined by gravity.[2]
Although Newtonian physics made a clear distinction between weight and mass, the term weight continued to be commonly used when people meant mass. This led the 3rd General Conference on Weights and Measures (CGPM) of 1901 to officially declare «The word weight denotes a quantity of the same nature as a force: the weight of a body is the product of its mass and the acceleration due to gravity», thus distinguishing it from mass for official usage.
Relativity[edit]
In the 20th century, the Newtonian concepts of absolute time and space were challenged by relativity. Einstein’s equivalence principle put all observers, moving or accelerating, on the same footing. This led to an ambiguity as to what exactly is meant by the force of gravity and weight. A scale in an accelerating elevator cannot be distinguished from a scale in a gravitational field. Gravitational force and weight thereby became essentially frame-dependent quantities. This prompted the abandonment of the concept as superfluous in the fundamental sciences such as physics and chemistry. Nonetheless, the concept remained important in the teaching of physics. The ambiguities introduced by relativity led, starting in the 1960s, to considerable debate in the teaching community as how to define weight for their students, choosing between a nominal definition of weight as the force due to gravity or an operational definition defined by the act of weighing.[2]
Definitions[edit]
This top-fuel dragster can accelerate from zero to 160 kilometres per hour (99 mph) in 0.86 seconds. This is a horizontal acceleration of 5.3 g. Combined with the vertical g-force in the stationary case the Pythagorean theorem yields a g-force of 5.4 g. It is this g-force that causes the driver’s weight if one uses the operational definition. If one uses the gravitational definition, the driver’s weight is unchanged by the motion of the car.
Several definitions exist for weight, not all of which are equivalent.[3][11][12][13]
Gravitational definition[edit]
The most common definition of weight found in introductory physics textbooks defines weight as the force exerted on a body by gravity.[1][13] This is often expressed in the formula W = mg, where W is the weight, m the mass of the object, and g gravitational acceleration.
In 1901, the 3rd General Conference on Weights and Measures (CGPM) established this as their official definition of weight:
«The word weight denotes a quantity of the same nature[Note 1] as a force: the weight of a body is the product of its mass and the acceleration due to gravity.»
— Resolution 2 of the 3rd General Conference on Weights and Measures[15][16]
This resolution defines weight as a vector, since force is a vector quantity. However, some textbooks also take weight to be a scalar by defining:
«The weight W of a body is equal to the magnitude Fg of the gravitational force on the body.»[17]
The gravitational acceleration varies from place to place. Sometimes, it is simply taken to have a standard value of 9.80665 m/s2, which gives the standard weight.[15]
The force whose magnitude is equal to mg newtons is also known as the m kilogram weight (which term is abbreviated to kg-wt)[18]
Left: A spring scale measures weight, by seeing how much the object pushes on a spring (inside the device). On the Moon, an object would give a lower reading. Right: A balance scale indirectly measures mass, by comparing an object to references. On the Moon, an object would give the same reading, because the object and references would both become lighter.
Operational definition[edit]
In the operational definition, the weight of an object is the force measured by the operation of weighing it, which is the force it exerts on its support.[11] Since W is the downward force on the body by the centre of earth and there is no acceleration in the body, there exists an opposite and equal force by the support on the body. Also it is equal to the force exerted by the body on its support because action and reaction have same numerical value and opposite direction. This can make a considerable difference, depending on the details; for example, an object in free fall exerts little if any force on its support, a situation that is commonly referred to as weightlessness. However, being in free fall does not affect the weight according to the gravitational definition. Therefore, the operational definition is sometimes refined by requiring that the object be at rest.[citation needed] However, this raises the issue of defining «at rest» (usually being at rest with respect to the Earth is implied by using standard gravity).[citation needed] In the operational definition, the weight of an object at rest on the surface of the Earth is lessened by the effect of the centrifugal force from the Earth’s rotation.
The operational definition, as usually given, does not explicitly exclude the effects of buoyancy, which reduces the measured weight of an object when it is immersed in a fluid such as air or water. As a result, a floating balloon or an object floating in water might be said to have zero weight.
ISO definition[edit]
In the ISO International standard ISO 80000-4:2006,[19] describing the basic physical quantities and units in mechanics as a part of the International standard ISO/IEC 80000, the definition of weight is given as:
Definition
,
- where m is mass and g is local acceleration of free fall.
Remarks
- When the reference frame is Earth, this quantity comprises not only the local gravitational force, but also the local centrifugal force due to the rotation of the Earth, a force which varies with latitude.
- The effect of atmospheric buoyancy is excluded in the weight.
- In common parlance, the name «weight» continues to be used where «mass» is meant, but this practice is deprecated.
— ISO 80000-4 (2006)
The definition is dependent on the chosen frame of reference. When the chosen frame is co-moving with the object in question then this definition precisely agrees with the operational definition.[12] If the specified frame is the surface of the Earth, the weight according to the ISO and gravitational definitions differ only by the centrifugal effects due to the rotation of the Earth.
Apparent weight[edit]
In many real world situations the act of weighing may produce a result that differs from the ideal value provided by the definition used. This is usually referred to as the apparent weight of the object. A common example of this is the effect of buoyancy, when an object is immersed in a fluid the displacement of the fluid will cause an upward force on the object, making it appear lighter when weighed on a scale.[20] The apparent weight may be similarly affected by levitation and mechanical suspension. When the gravitational definition of weight is used, the operational weight measured by an accelerating scale is often also referred to as the apparent weight.[21]
Mass[edit]
An object with mass m resting on a surface and the corresponding free body diagram of just the object showing the forces acting on it. Notice that the amount of force that the table is pushing upward on the object (the N vector) is equal to the downward force of the object’s weight (shown here as mg, as weight is equal to the object’s mass multiplied with the acceleration due to gravity): because these forces are equal, the object is in a state of equilibrium (all the forces and moments acting on it sum to zero).
In modern scientific usage, weight and mass are fundamentally different quantities: mass is an intrinsic property of matter, whereas weight is a force that results from the action of gravity on matter: it measures how strongly the force of gravity pulls on that matter. However, in most practical everyday situations the word «weight» is used when, strictly, «mass» is meant.[8][22] For example, most people would say that an object «weighs one kilogram», even though the kilogram is a unit of mass.
The distinction between mass and weight is unimportant for many practical purposes because the strength of gravity does not vary too much on the surface of the Earth. In a uniform gravitational field, the gravitational force exerted on an object (its weight) is directly proportional to its mass. For example, object A weighs 10 times as much as object B, so therefore the mass of object A is 10 times greater than that of object B. This means that an object’s mass can be measured indirectly by its weight, and so, for everyday purposes, weighing (using a weighing scale) is an entirely acceptable way of measuring mass. Similarly, a balance measures mass indirectly by comparing the weight of the measured item to that of an object(s) of known mass. Since the measured item and the comparison mass are in virtually the same location, so experiencing the same gravitational field, the effect of varying gravity does not affect the comparison or the resulting measurement.
The Earth’s gravitational field is not uniform but can vary by as much as 0.5%[23] at different locations on Earth (see Earth’s gravity). These variations alter the relationship between weight and mass, and must be taken into account in high-precision weight measurements that are intended to indirectly measure mass. Spring scales, which measure local weight, must be calibrated at the location at which the objects will be used to show this standard weight, to be legal for commerce.[citation needed]
This table shows the variation of acceleration due to gravity (and hence the variation of weight) at various locations on the Earth’s surface.[24]
| Location | Latitude | m/s2 | Absolute difference from equator | Percentage difference from equator |
|---|---|---|---|---|
| Equator | 0° | 9.7803 | 0.0000 | 0% |
| Sydney | 33°52′ S | 9.7968 | 0.0165 | 0.17% |
| Aberdeen | 57°9′ N | 9.8168 | 0.0365 | 0.37% |
| North Pole | 90° N | 9.8322 | 0.0519 | 0.53% |
The historical use of «weight» for «mass» also persists in some scientific terminology – for example, the chemical terms «atomic weight», «molecular weight», and «formula weight», can still be found rather than the preferred «atomic mass», etc.
In a different gravitational field, for example, on the surface of the Moon, an object can have a significantly different weight than on Earth. The gravity on the surface of the Moon is only about one-sixth as strong as on the surface of the Earth. A one-kilogram mass is still a one-kilogram mass (as mass is an intrinsic property of the object) but the downward force due to gravity, and therefore its weight, is only one-sixth of what the object would have on Earth. So a man of mass 180 pounds weighs only about 30 pounds-force when visiting the Moon.
SI units[edit]
In most modern scientific work, physical quantities are measured in SI units. The SI unit of weight is the same as that of force: the newton (N) – a derived unit which can also be expressed in SI base units as kg⋅m/s2 (kilograms times metres per second squared).[22]
In commercial and everyday use, the term «weight» is usually used to mean mass, and the verb «to weigh» means «to determine the mass of» or «to have a mass of». Used in this sense, the proper SI unit is the kilogram (kg).[22]
As of 20 May 2019, the kilogram, which is essential to evaluate the weight of an object, has been redefined in terms of Planck’s constant. The new definition does not affect the actual amount of the material but increases the measurement’s quality and decreases the uncertainty associated with it.[25]
Prior to using Planck’s constant, a physical object was used as a standard. The object, located in a vault in Sèvres, France, has fluctuated by approximately 50 micrograms of its mass since it was first introduced in 1889.[26] Consequently, the following must be true. Mass, which should be the same whether on earth or the moon for example, is only valid on earth since it needs to be referenced. Also, comparing a weight measurement to a standard that changes with time cannot be used as a reference without citing the actual value of it at the time and moment it was used as such. Therefore, to redefine the kilogram all National Metrology Institutes (NMIs) involved determined the new value of Planck’s constant by evaluating a mass which was calibrated against the IPK.[27] To this extent one kilogram is equal to h/(6.62607015×10^(-34) ) m^(-2) s which equals 1 m^(-2) s.
A kilogram has remained the same quantity it was before the redefinition.[27] But as of May 2019, the weights measured and recorded can be traced back and used as comparison for current and future work.
Pound and other non-SI units[edit]
In United States customary units, the pound can be either a unit of force or a unit of mass.[28] Related units used in some distinct, separate subsystems of units include the poundal and the slug. The poundal is defined as the force necessary to accelerate an object of one-pound mass at 1 ft/s2, and is equivalent to about 1/32.2 of a pound-force. The slug is defined as the amount of mass that accelerates at 1 ft/s2 when one pound-force is exerted on it, and is equivalent to about 32.2 pounds (mass).
The kilogram-force is a non-SI unit of force, defined as the force exerted by a one-kilogram mass in standard Earth gravity (equal to 9.80665 newtons exactly). The dyne is the cgs unit of force and is not a part of SI, while weights measured in the cgs unit of mass, the gram, remain a part of SI.
Sensation[edit]
The sensation of weight is caused by the force exerted by fluids in the vestibular system, a three-dimensional set of tubes in the inner ear.[dubious – discuss] It is actually the sensation of g-force, regardless of whether this is due to being stationary in the presence of gravity, or, if the person is in motion, the result of any other forces acting on the body such as in the case of acceleration or deceleration of a lift, or centrifugal forces when turning sharply.
Measuring[edit]
Weight is commonly measured using one of two methods. A spring scale or hydraulic or pneumatic scale measures local weight, the local force of gravity on the object (strictly apparent weight force). Since the local force of gravity can vary by up to 0.5% at different locations, spring scales will measure slightly different weights for the same object (the same mass) at different locations. To standardize weights, scales are always calibrated to read the weight an object would have at a nominal standard gravity of 9.80665 m/s2 (approx. 32.174 ft/s2). However, this calibration is done at the factory. When the scale is moved to another location on Earth, the force of gravity will be different, causing a slight error. So to be highly accurate and legal for commerce, spring scales must be re-calibrated at the location at which they will be used.
A balance on the other hand, compares the weight of an unknown object in one scale pan to the weight of standard masses in the other, using a lever mechanism – a lever-balance. The standard masses are often referred to, non-technically, as «weights». Since any variations in gravity will act equally on the unknown and the known weights, a lever-balance will indicate the same value at any location on Earth. Therefore, balance «weights» are usually calibrated and marked in mass units, so the lever-balance measures mass by comparing the Earth’s attraction on the unknown object and standard masses in the scale pans. In the absence of a gravitational field, away from planetary bodies (e.g. space), a lever-balance would not work, but on the Moon, for example, it would give the same reading as on Earth. Some balances are marked in weight units, but since the weights are calibrated at the factory for standard gravity, the balance will measure standard weight, i.e. what the object would weigh at standard gravity, not the actual local force of gravity on the object.
If the actual force of gravity on the object is needed, this can be calculated by multiplying the mass measured by the balance by the acceleration due to gravity – either standard gravity (for everyday work) or the precise local gravity (for precision work). Tables of the gravitational acceleration at different locations can be found on the web.
Gross weight is a term that is generally found in commerce or trade applications, and refers to the total weight of a product and its packaging. Conversely, net weight refers to the weight of the product alone, discounting the weight of its container or packaging; and tare weight is the weight of the packaging alone.
Relative weights on the Earth and other celestial bodies[edit]
The table below shows comparative gravitational accelerations at the surface of the Sun, the Earth’s moon, each of the planets in the solar system. The “surface” is taken to mean the cloud tops of the gas giants (Jupiter, Saturn, Uranus and Neptune). For the Sun, the surface is taken to mean the photosphere. The values in the table have not been de-rated for the centrifugal effect of planet rotation (and cloud-top wind speeds for the gas giants) and therefore, generally speaking, are similar to the actual gravity that would be experienced near the poles.
| Body | Multiple of Earth gravity |
Surface gravity m/s2 |
|---|---|---|
| Sun | 27.90 | 274.1 |
| Mercury | 0.3770 | 3.703 |
| Venus | 0.9032 | 8.872 |
| Earth | 1 (by definition) | 9.8226[29] |
| Moon | 0.1655 | 1.625 |
| Mars | 0.3895 | 3.728 |
| Jupiter | 2.640 | 25.93 |
| Saturn | 1.139 | 11.19 |
| Uranus | 0.917 | 9.01 |
| Neptune | 1.148 | 11.28 |
See also[edit]
- Human body weight – Person’s mass or weight
- Tare weight
- weight – Unit of weight the English unit
Notes[edit]
- ^ The phrase «quantity of the same nature» is a literal translation of the French phrase grandeur de la même nature. Although this is an authorized translation, VIM 3 of the International Bureau of Weights and Measures recommends translating grandeurs de même nature as quantities of the same kind.[14]
References[edit]
- ^ a b Richard C. Morrison (1999). «Weight and gravity — the need for consistent definitions». The Physics Teacher. 37 (1): 51. Bibcode:1999PhTea..37…51M. doi:10.1119/1.880152.
- ^ a b c d e f g h Igal Galili (2001). «Weight versus gravitational force: historical and educational perspectives». International Journal of Science Education. 23 (10): 1073. Bibcode:2001IJSEd..23.1073G. doi:10.1080/09500690110038585. S2CID 11110675.
- ^ a b Gat, Uri (1988). «The weight of mass and the mess of weight». In Richard Alan Strehlow (ed.). Standardization of Technical Terminology: Principles and Practice – second volume. ASTM International. pp. 45–48. ISBN 978-0-8031-1183-7.
- ^ Knight, Randall D. (2004). Physics for Scientists and Engineers: a Strategic Approach. San Francisco, USA: Addison–Wesley. pp. 100–101. ISBN 0-8053-8960-1.
- ^ Bauer, Wolfgang and Westfall, Gary D. (2011). University Physics with Modern Physics. New York: McGraw Hill. p. 103. ISBN 978-0-07-336794-1.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Serway, Raymond A. and Jewett, John W. Jr. (2008). Physics for Scientists and Engineers with Modern Physics. USA: Thompson. p. 106. ISBN 978-0-495-11245-7.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Hewitt, Paul G. (2001). Conceptual Physics. USA: Addison–Wesley. pp. 159. ISBN 0-321-05202-1.
- ^ a b The National Standard of Canada, CAN/CSA-Z234.1-89 Canadian Metric Practice Guide, January 1989:
- 5.7.3 Considerable confusion exists in the use of the term «weight». In commercial and everyday use, the term «weight» nearly always means mass. In science and technology «weight» has primarily meant a force due to gravity. In scientific and technical work, the term «weight» should be replaced by the term «mass» or «force», depending on the application.
- 5.7.4 The use of the verb «to weigh» meaning «to determine the mass of», e.g., «I weighed this object and determined its mass to be 5 kg,» is correct.
- ^ Sur Das (1590s). «Weighing Grain». Baburnama.
- ^ http://www.averyweigh-tronix.com/museum Archived 2013-02-28 at the Wayback Machine accessed 29 March 2013.
- ^ a b Allen L. King (1963). «Weight and weightlessness». American Journal of Physics. 30 (5): 387. Bibcode:1962AmJPh..30..387K. doi:10.1119/1.1942032.
- ^ a b A. P. French (1995). «On weightlessness». American Journal of Physics. 63 (2): 105–106. Bibcode:1995AmJPh..63..105F. doi:10.1119/1.17990.
- ^ a b Galili, I.; Lehavi, Y. (2003). «The importance of weightlessness and tides in teaching gravitation» (PDF). American Journal of Physics. 71 (11): 1127–1135. Bibcode:2003AmJPh..71.1127G. doi:10.1119/1.1607336.
- ^ Working Group 2 of the Joint Committee for Guides in Metrology (JCGM/WG 2) (2008). International vocabulary of metrology – Basic and general concepts and associated terms (VIM) – Vocabulaire international de métrologie – Concepts fondamentaux et généraux et termes associés (VIM) (PDF) (JCGM 200:2008) (in English and French) (3rd ed.). BIPM. Note 3 to Section 1.2.
- ^ a b «Resolution of the 3rd meeting of the CGPM (1901)». BIPM.
- ^ David B. Newell; Eite Tiesinga, eds. (2019). The International System of Units (SI) (PDF) (NIST Special publication 330, 2019 ed.). Gaithersburg, MD: NIST. p. 46.
- ^ Halliday, David; Resnick, Robert; Walker, Jearl (2007). Fundamentals of Physics. Vol. 1 (8th ed.). Wiley. p. 95. ISBN 978-0-470-04473-5.
- ^ Chester, W. Mechanics. George Allen & Unwin. London. 1979. ISBN 0-04-510059-4. Section 3.2 at page 83.
- ^ ISO 80000-4:2006, Quantities and units — Part 4: Mechanics
- ^ Bell, F. (1998). Principles of mechanics and biomechanics. Stanley Thornes Ltd. pp. 174–176. ISBN 978-0-7487-3332-3.
- ^ Galili, Igal (1993). «Weight and gravity: teachers’ ambiguity and students’ confusion about the concepts». International Journal of Science Education. 15 (2): 149–162. Bibcode:1993IJSEd..15..149G. doi:10.1080/0950069930150204.
- ^ a b c A. Thompson & B. N. Taylor (March 3, 2010) [July 2, 2009]. «The NIST Guide for the use of the International System of Units, Section 8: Comments on Some Quantities and Their Units». Special Publication 811. NIST. Retrieved 2010-05-22.
- ^ Hodgeman, Charles, ed. (1961). Handbook of Chemistry and Physics (44th ed.). Cleveland, USA: Chemical Rubber Publishing Co. pp. 3480–3485.
- ^ Clark, John B (1964). Physical and Mathematical Tables. Oliver and Boyd.
- ^ Yadav, S., & Aswal, D. K. (2020, February 25). Redefined SI Units and Their Implications. Mapan, pp. 1-9.
- ^ Jeffrey-Wilensky, J. (2019, May 20). The definition of the kilogram just changed. Here’s what that means. Retrieved from NBC News: https://www.nbcnews.com/mach/science/definition-kilogram-just-changed-here-s-what-means-ncna1007731
- ^ a b Ehtesham, B., John, T., Yadav, S., Singh, H. K., Mandal, G., & Singh, N. (2020). Journey of Kilogram from Physical Constant to Universal Physical Constant (h) via Artefact: A Brief Review. MAPAN — Journal of Metrology Society of India, 1-9
- ^ «Common Conversion Factors, Approximate Conversions from U.S. Customary Measures to Metric». Nist. National Institute of Standards and Technology. 13 January 2010. Retrieved 2013-09-03.
- ^ This value excludes the adjustment for centrifugal force due to Earth’s rotation and is therefore greater than the 9.80665 m/s2 value of standard gravity.
Понятие и определения
Массой (обозначается буквой m) называют одну из физических величин, таких, как объём, определяющих количество вещества в объекте. Существует несколько явлений, которые позволяют её оценить. Среди теоретиков есть мнение, что некоторые из этих явлений могут быть независимы друг от друга, но в ходе экспериментов не обнаружено различий в результатах от способа измерений массы:
- Инерционная. Определяется сопротивлением тела ускорению силой.
- Активная и пассивная гравитационные. Измеряется силой взаимодействия гравитационных полей объектов.
Человек чувствует свою массу находясь в контакте с другой поверхностью. Это может быть стулом, земной твердью, креслом космонавта во время ускорения в ракете. В этих примерах речь идёт о величине, которую физики называют весом, а субъективно воспринимающимся как кажущийся вес.
Он равен фактической измеряемой массе почти во всех бытовых случаях, за следующими исключениями:
- Тело получает ускорение с вертикальной составляющей по отношению к земле. Например, в лифте или самолёте.
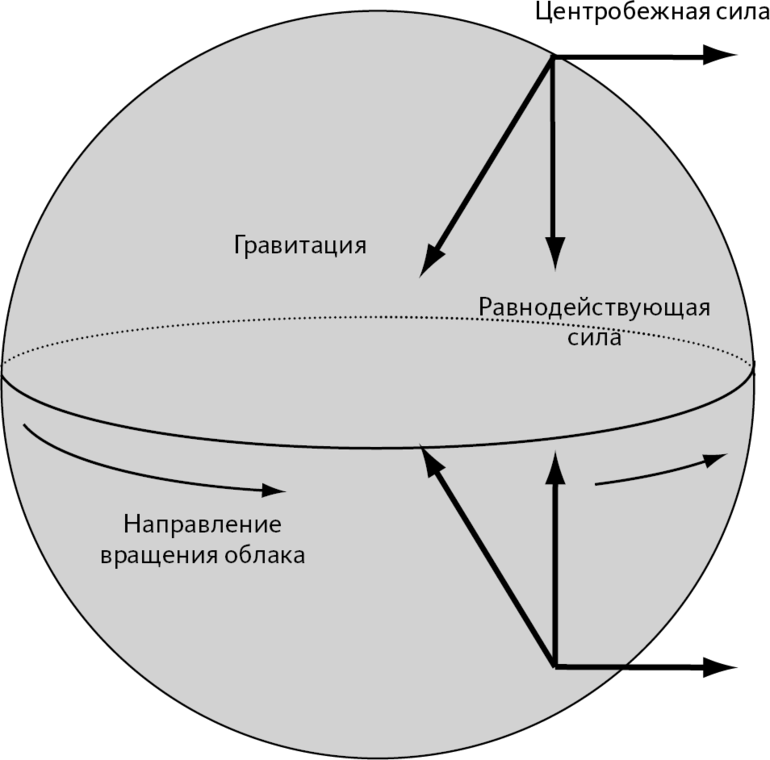
- Кроме гравитации Земли, на тело действуют другие силы — центробежная, гравитационная другого от тела, архимедова.
Гравитационный подход
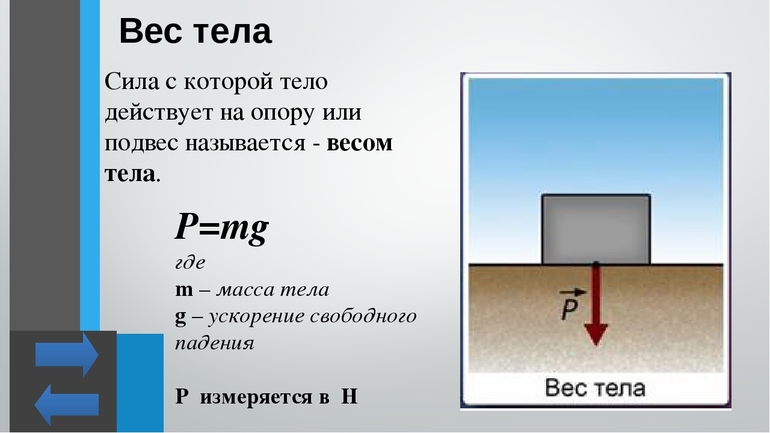
В большинстве случаев при определении понятия веса (принятое обозначение — P, по-латински пишется как pondus) оперируют так называемым гравитационным определением. В учебниках физики формула веса для тела описывает величину как силу, действующую на объект в результате земного притяжения. На языке математики это определяется выражением P=mg, где:
- m — масса;
- g — гравитационное ускорение.
Из формулы вытекает, в чём измеряется вес: количественно он рассчитывается в тех же единицах, что и сила. Поэтому, согласно Международной системе единиц (СИ), P измеряется в Ньютонах.
Гравитационное поле Земли не является однородным и варьируется в пределах 0,5% по поверхности планеты. Соответственно, величина g также непостоянна. Общепринятым считается значение, называемое стандартным и равное 9,80665 м/с2. В различных местах на поверхности Земли фактическое ускорение свободного падения составляет (м/с2):
- экватор — 9,7803;
- Сидней — 9,7968;
- Москва — 9,8155;
- Северный полюс — 9,8322.
В 1901 году третья Генеральная конференция по весам и мерам установила: вес означает количество такой же природы, что и сила, То есть определила его как вектор, так как сила — векторная величина. Тем не менее некоторые школьные учебники физики и сейчас принимают P за скаляр.
Контактное определение
Другой подход описывает явление с позиции понимания какую силу называют весом тела. В этом случае P определяется процедурой взвешивания и означает силу, с которой объект действует на опору. Этот подход предполагает различие результатов в зависимости от деталей.
Например, объект в свободном падении оказывает незначительное воздействие на опору, однако, нахождение в невесомости не меняет вес в соответствии с гравитационным определением. Следовательно, подобный подход требует нахождения исследуемого тела в состоянии покоя, под действием стандартной гравитации без влияния центробежной силы вращения Земли.
Кроме того, контактное определение не исключает искажения от плавучести, которое уменьшает измеренный вес объекта. В воздухе на тела также действует сила, аналогичная влияющей на погружённое в воде. Для объектов с низкой плотностью эффект влияния становится более заметен. Примером тому может служить наполненный гелием воздушный шар, обладающий отрицательным весом. В общем смысле любое воздействие оказывает искажающий эффект на контактный вес, например:
- Центробежная сила. Поскольку Земля вращается, объекты на поверхности подвергаются воздействию центробежных сил, более выраженных к экватору.
- Гравитационное влияние других астрономических тел. Солнце и Луна притягивают объекты на земной поверхности в той или иной степени в зависимости от расстояния. Это влияние незначительно на бытовом уровне, но находит заметное отражение в таких явлениях, как морские приливы и отливы.
- Магнетизм. Сильные магнитные поля способны заставить левитировать некоторые подверженные влиянию объекты.
История понятия
Понятия тяжести и лёгкости в качестве неотъемлемых свойств физических тел упоминаются ещё древнегреческими философами. Платон описывал вес как естественную тенденцию предметов к поиску себе подобных. Для Аристотеля лёгкость была свойством в восстановлении порядка основных элементов: воздуха, земли, огня и воды. Архимед рассматривал вес как качество, противоположное плавучести. Первое контактное определение было дано Евклидом, описывающее величину как лёгкость одной вещи по сравнению с другой, измеряемую балансом.
Когда средневековые учёные обнаружили, что на практике скорость падающего предмета со временем возрастала. Они изменили концепцию веса для сохранения причинно-следственных связей между явлениями. Понятие было разделено для тел в состоянии покоя и находящихся в гравитационном падении.
Значительных результатов в теории добился Галилей, пришедший к выводу, что величина пропорциональна количеству вещества в объекте, а не скорости его движения, как предполагала Аристотелева физика. Открытие Ньютоном закона всемирного тяготения привело к принципиальному отделению веса от фундаментального свойства объектов, связанных с инерцией. Факторы окружающей среды и плавучесть учёный считал искажением условий измерения. Для подобных обстоятельств он ввёл термин кажущийся вес.
В XX веке ньютоновские концепции абсолютного времени и пространства были поставлены под сомнение работами Эйнштейна. Теория относительности поставила всех наблюдателей, движущихся и ускоряющихся, в разные условия. Это привело к двусмысленности относительно того, что именно подразумевается под массой, которая вместе с гравитационной силой стала по существу зависящей от системы отсчёта величиной.
Неоднозначности, порождённые относительностью, привели к серьёзным дебатам в педагогическом сообществе о том, как определять вес для учеников и что им должно называться. Выбор стал лежать между пониманием его как силы, вызванной гравитацией Земли, и контактным определением, вытекающим из акта взвешивания.
Различия с массой
Путаница в понимании того, чем отличается масса от веса, свойственна для людей, не изучающих физику подробно. Этому есть простое объяснение — как правило, эти термины используются в повседневной жизни взаимозаменяемо. В общем случае, если тело находится на поверхности земли и неподвижно, значение массы будет равно скаляру веса в килограммах. Таблица, проясняющая разницу между понятиями, выглядит так:
| Масса | Вес |
| Является свойством материи. Постоянна всегда. | Зависит от действия силы тяжести. |
| У материального объекта никогда не бывает равна нулю. | Может быть равен нулю при определённых условиях. |
| Не меняется в зависимости от местоположения. | Уменьшается или увеличивается в разных местах Земли или в зависимости от высоты над её поверхностью. |
| Является скалярной величиной. | Вектор с направлением к центру земли или к другому гравитационному центру. |
| Может быть измерена с помощью баланса | Измеряется с помощью пружинных весов. |
| Как правило, измеряется в граммах и килограммах. | Единица у силы и веса одна — Ньютон (обозначается как Н) |
Главное отличительное свойство массы заключается в том, что для классической динамики она является конкретной инвариантной величиной для каждого тела. Общая теория относительности описывает переход массы в энергию и наоборот.
Обычно численное значение между m и P на Земле строго пропорционально. На бытовом уровне чтобы узнать вес тела с известной массой, достаточно помнить, что объекты обычно весят в ньютонах приблизительно в 10 раз больше значения m в килограммах.
Способы измерения
Фактически вес можно измерить как силу реакции опоры на массу, появляющуюся в точке приложения. Величина возникновения этой силы по значению равна искомому P. Определить её можно с помощью пружинных весов. Поскольку сила тяжести, вызывающая фиксируемое отклонение на шкале, может варьироваться в разных местах, значения также будут отличаться. Для стандартизации измерительные приборы такого типа всегда калибруются на 9,80665 м/с2 в заводских условиях, а затем повторно в том месте, где будут использоваться.
Для измерения массы применяют рычажный механизм. Поскольку любые изменения в гравитации будут одинаково воздействовать на известные и неизвестные массы, балансный способ позволяет иметь в результате одинаковые значения в любом месте Земли. Весовые коэффициенты в этом случае калибруются и маркируются в единицах массы, поэтому балансировочный рычаг позволяет найти массу, сравнивая воздействие притяжения на искомый объект с воздействием на эталон.
При отсутствии гравитационного поля вдали от крупных астрономических тел, баланс рычага работать не будет, но, например, на Луне он покажет те же значения, что и на Земле. Некоторые подобные инструменты могут быть размечены в единицах веса, но, поскольку они калибруются на заводе-изготовителе для стандартной гравитации, то будут показывать P для условий, под которые они настроены.
Это значит, что рычажные весы не предназначены для измерения локальной силы тяжести, воздействующей на объект. Точный вес можно определить расчётным путём, умножив массу на значение локальной гравитации из соответствующих таблиц.
На других планетах
В отличие от массы, вес тела в разных местах варьируется в зависимости от изменения значения гравитационного ускорения. Величина силы притяжения на других планетах, как и на Земле, зависит не только от их массы, но и от того, насколько удалена поверхность от центра тяжести.
В таблице ниже приведены сравнительные гравитационные ускорения на других планетах, Солнце и Луне. Под поверхностью для газовых гигантов (Юпитер, Сатурн, Уран и Нептун) подразумеваются их внешние облачные слои, для Солнца — фотосфера. Значения в таблице указаны без учёта центробежного вращения и отражают фактическую гравитацию, наблюдаемую вблизи полюсов.
| Астрономический объект | Насколько гравитация превышает земную | Поверхностное ускорение м/с2 |
| Солнце | 27,9 | 274,1 |
| Меркурий | 0,377 | 3,703 |
| Венера | 0,9032 | 8,872 |
| Земной шар | 1 | 9,8226 |
| Луна | 0,1655 | 1,625 |
| Марс | 0,3895 | 3,728 |
| Юпитер | 2,64 | 25,93 |
| Сатурн | 1,139 | 11,19 |
| Уран | 0,917 | 9,01 |
| Нептун | 1,148 | 11,28 |
Для того чтобы получить собственный вес на другой планете, необходимо просто умножить его на число кратности из соответствующего столбика. Чем ближе к центру планеты делать замер, тем значение будет выше, и наоборот. Поэтому, несмотря на то что сила притяжения Юпитера из-за огромной массы в 316 раз превышает земную, вес на уровне облаков, из-за большой их удалённости от центра масс, выглядит не таким впечатляющим, как можно было бы ожидать.
Ещё один интересный эффект, называемый невесомостью, характерный не только для космоса. Его можно наблюдать при различных обстоятельствах и на Земле. Например, при свободном падении нет опоры, к которой была бы приложена сила, а значит вес будет равен нулю, несмотря на присутствие ускорения силы тяжести и массы.
Подобный феномен происходит с космонавтами Международной космической станции на орбите Земли. Фактически она всегда падает вместе со своими обитателями на поверхность планеты, поэтому её обитатели постоянно находятся в состоянии невесомости.
Таким образом, главное правило, объясняющее наблюдаемые феномены и позволяющее избежать путаницы с массой, выглядит так: значение P всегда измеряется с помощью контактных весов, помещённых между объектом и опорной поверхностью. Именно поэтому тело, размещённое на весах и падающее вместе с ними, не будет давить на прибор, а шкала, соответственно, покажет нулевое значение.
>
Содержание:
Вес тела:
Множество тел на Земле находятся в состоянии покоя относительно ее поверхности. Почему же тела, на которые всегда действует сила тяготения, не изменяют своего положения и скорости под действием этой силы?
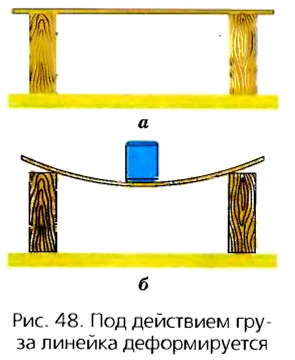
Ответ на этот вопрос найдем при проведении опыта. С этой целью положим линейку на две подставки и поставим на нее груз (рис. 48). Линейка деформируется. Следовательно, груз подействовал на линейку и изменил ее форму, деформировал. А при деформации возникла сила упругости, которая уравновесила силу тяготения, и груз прекратил движение к Земле.
Закрепим в штативе резиновую нить, а к ее концу прикрепим шарик. Если отпустим шарик, то он начнет двигаться вниз и будет растягивать нить до тех пор, пока сила упругости не уравновесит силу тяготения.
В обоих случаях на груз и шарик действовала сила тяготения, поэтому они, в свою очередь, действовали на линейку или резиновую нить.
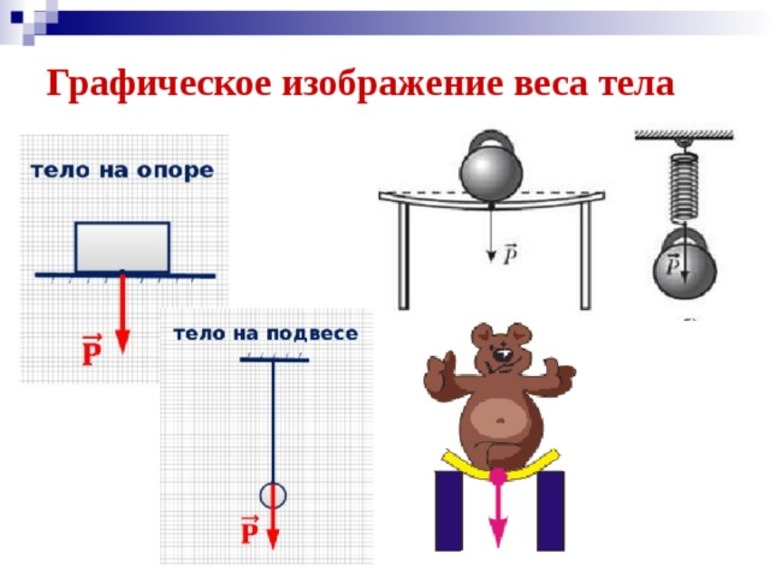
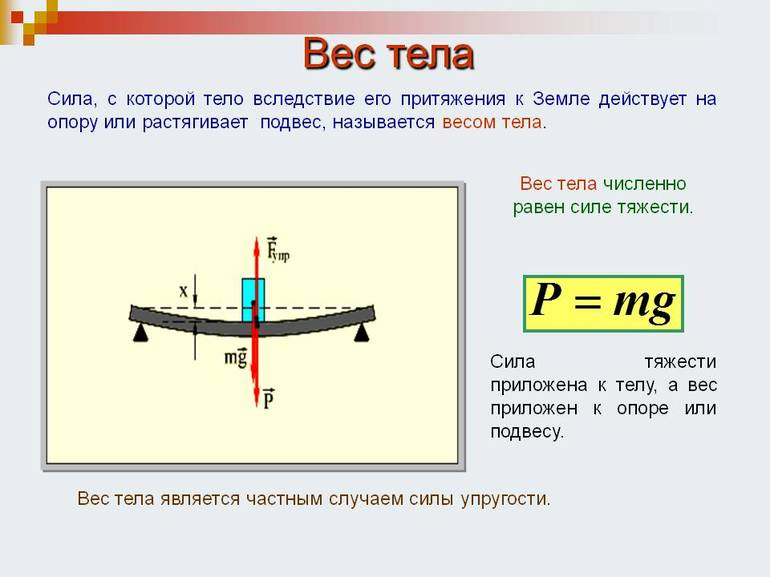
Что такое вес тела
Силу, с которой тело действует на опору или подвес, называют весом тела.
Вес зависит от механического состояния тела. Если тело неподвижно относительно опоры или подвеса или движется равномерно и прямолинейно, то вес по значению и направлению совпадает с силой тяготения.
Для этого случая можно записать, что
Однако между этими силами есть и существенные различия. Так, они приложены к различным телам. Если сила тяготения приложена к данному телу, то вес приложен к опоре или подвесу (рис. 49, 50).
Отличия проявляются и тогда, когда тело и опора свободно падают под действием силы тяготения. В этом случае вес исчезает и возникает состояние невесомости.
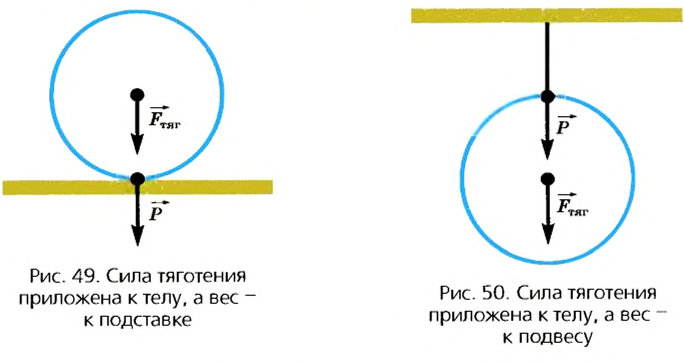
Такую особенность веса можно наблюдать в сравнительно простых опытах. Повесим на нити, закрепленной в штативе, металлический динамометр, к крючку которого прикреплены грузы. Стрелка покажет определенное значение веса грузов. Теперь перережем нить -динамометр с грузом начнет падать. В момент падения стрелка динамометра сместится на деление «ноль» (рис. 51). Таким образом, при свободном падении тела вес тела исчезает, возникает состояние невесомости.
Невесомость ощущают пилоты и космонавты. Если космический корабль движется вокруг Земли, то он все время как бы падает на Землю и все тела в его кабине теряют вес (рис. 52). В таких условиях много обычных явлений происходит своеобразно. Так, вода вне сосуда приобретает шарообразную форму и свободно плавает в пространстве. Брошенный предмет будет двигаться от стенки к стенке прямолинейно, не останавливаясь.
- Заказать решение задач по физике
Вес и невесомость
Вес — это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес. Вес тела обозначается буквой 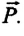
Случай, когда вес тела не меняется
Если тело находится в состоянии покоя или движется прямолинейно равномерно по горизонтальной поверхности, то его вес не изменяется. Почему?
Согласно III закону Ньютона, вес тела действует на опору и равен по модулю и противоположен по направлению силе реакции опоры 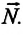
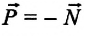
Если тело на подвесе находится в состоянии покоя или вместе с подвесом движется прямолинейно равномерно, то, согласно III закону Ньютона, вес этого тела, действующий на подвес, равен по модулю и направлен противоположно силе натяжения нити 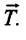
Согласно II закону Ньютона, уравнение движения для тела, находящегося в состоянии покоя или прямолинейного равномерного движения на горизонтальной опоре, записывается в виде:
Принимая во внимание, что результирующая сила равна векторной сумме силы тяжести и силы реакции опоры, уравнение движения примет вид:
Для решения уравнения выбирается ось координат, определяются проекции векторов сил на эту ось и, приняв во внимание знак проекций, записывают их в уравнение. За положительное направление оси 
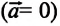
Отсюда видно, что вес тела, находящегося в состоянии покоя или прямолинейного равномерного движения, численно равен модулю силы тяжести:
Случай, когда вес тела меняется
Если тело вместе с опорой (или с подвесом) движется с ускорением 
Предположим, что тело вместе с опорой движется вертикально вверх с ускорением 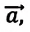
Если направить координатную ось вдоль направления движения (с), получим:
Отсюда видно, что вес тела, движущегося вместе с опорой вертикально вверх с ускорением 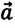
Ясно, что если тело вместе с опорой будет двигаться в направлении действия силы тяжести, то его вес уменьшится:
Случай, когда вес тела равен нулю — невесомость
Если тело движется только под действием гравитационной силы, то есть его ускорение будет равно ускорению свободного падения 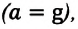
- Закон всемирного тяготения
- Свободное падение тела
- Равнодействующая сила и движение тела под действием нескольких сил
- Сила давления в физике и единицы давления
- Сила упругости в физике и закон Гука
- Деформация в физике
- Плотность вещества в физике
- Сила трения в физике
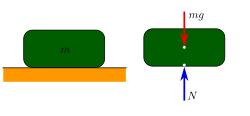
Из-за притяжения Земли все тела имеют вес.
Сила, с которой тело давит на опору или растягивает подвес, называют весом.
Рис. (1). Тело на опоре, тело на подвесе
Вес тела обозначают (P) и измеряют в ньютонах ((H)).
Вес неподвижного тела равен
P=mg
.
Формула определения веса неподвижного тела точно такая же, как и формула силы тяжести (см. предыдущую тему «Сила. Сила тяжести»). Однако вес тела и сила тяжести — не одно и то же.
Рис. (2). Сила тяжести и вес тела
Например, сила тяжести свободно падающего трёхкилограммового кирпича приблизительно составляет (30) (H), ((F = mg)), а его вес (P) в момент падения равен (0) (H) (так как кирпич находится в состоянии невесомости).
Если помещённое на опору или подвешенное тело неподвижно по отношению к Земле или находится в равномерном движении вверх или вниз, тогда вес тела не меняется.
Вес меняется, когда тело перемещается вверх или вниз с ускорением.
Во время поездки в лифте, если мы двигаемся с ускорением вверх, наш вес увеличивается, хотя сила тяжести остаётся неизменной.
Состояние невесомости — это состояние, когда тело не давит на опору и не растягивает подвес. Такое происходит, когда тело свободно падает под воздействием только силы гравитации.
Почему в космическом корабле есть состояние невесомости?
Потому что космический корабль, обращаясь вокруг Земли, находится в свободном падении (он всё время как бы падает на Землю, но пролетает мимо). Это происходит, когда космический корабль достигает 1-й космической скорости — 7,9 км/с.
Если скорость космического корабля была бы меньше, он упал бы на Землю, а если корабль достиг бы 2-й космической скорости — 11,2 км/с, он стал бы искусственным спутником Солнца.
Если скорость космического корабля достигнет 3-й космической скорости — 16,7 км/с, тогда корабль направится из Солнечной системы к другим звёздам.
К сожалению, до ближайшей звёздной системы Альфа Центавра нужно лететь (18000) лет, так как она находится на расстоянии (4) световых лет.
Интересно, что для того, чтобы достичь Луны, ракета должна развить скорость, равную (0,992) от второй космической скорости.
Источники:
Рис. 1. Тело на опоре, тело на подвесе. © ЯКласс.
Рис. 2. Сила тяжести и вес тела. © ЯКласс.