Трактовка понятий
В физике упругая деформация возникает из-за силы, равной по модулю оказываемому воздействию. Сила упругости для пружины (F) пропорциональна её удлинению. Для определения жесткости пружины зависимость записывается математически с помощью следующей формулы: F = k·x; где х — длина предмета после его растяжения, а k — коэффициент жесткости.
Формула считается частным случаем закона Гука, который используется для растяжимого тонкого стержня. Чрезмерное воздействие приводит к появлению разных дефектов. Для процесса характерны некоторые особенности, от чего зависит жесткость пружины:
- геометрические параметры детали;
- срок эксплуатации;
- значение коэффициента k, который при определённых условиях способствует снижению сжатия и сохранению силы на одинаковом уровне;
- тип используемого материала (сталь, сплав) в процессе изготовления пружины.
На практических занятиях по физике в 7 классе применяются изделия разных типов. В автомобилестроении используется цветовое обозначение. Для расчета коэффициента жесткости пружины специалисты ориентируются на формулу k=Gd 4 /8D 3 n, где:
- G — определяет модуль сдвига (свойство зависит, к примеру, от используемого сырья);
- d — диаметр куска проволоки (величина определяется в период производства путём проката, а результат записывается в технической документации);
- D — диаметр витков, которые получаются в результате намотки на проволоку (расчет осуществляется с учетом поставленных задач и зависит от нагрузки, оказываемой для сжатия объекта);
- n — количество витков в системе (показатель варьируется в значительном диапазоне, от чего зависят эксплуатационные характеристики предмета).
С помощью формулы может измеряться жёсткость цилиндрической пружины, используемой в разных механизмах. Показатель измеряется в Ньютонах и обозначается Н.
Практические занятия
Механики и физики обозначают с помощью k, c и D коэффициент упругости, пропорциональности, жесткости. Смысл математической записи одинаковый. Численно показатель равняется силе, которая создаёт колебания на одну единицу длины. На практических работах по физике используется в качестве последней величины 1 метр.
Чем выше k, тем больше сопротивление предмета относительно деформации. Дополнительно коэффициент показывает степень устойчивости тела к колебаниям со стороны внешней нагрузки. Параметр зависит от длины и диаметра винтового изделия, количества витков, сырья. Единица измерения жесткости пружины — Н/м.
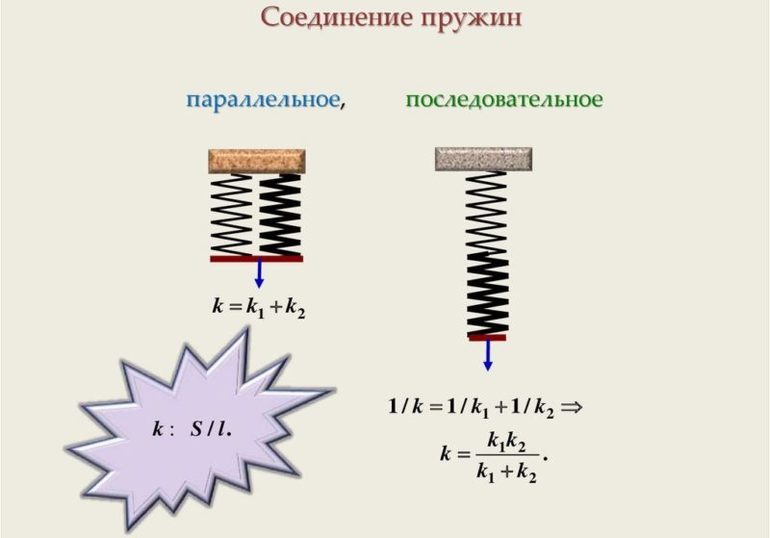
На практике перед школьниками и механиками может стоять более сложная задача, к примеру, найти общую жёсткость. В таком случае пружины соединены последовательным либо параллельным способом. В первом случае уменьшается суммарная жесткость. Если пружины расположены последовательно, используется следующая формула: 1/k = 1/k1 + 1/k2 + … + 1/ki, где:
- k — суммарная жёсткость соединений;
- k1 …ki — жёсткость каждого элемента системы;
- i — число пружин в цепи.
Если невесомые (расположены горизонтально) предметы соединены параллельно, значение общего k будет увеличиваться. Величина вычисляется по следующей формуле: k = k1 + k2 + … + ki.
Основная методика для вычислений
На практике коэффициент Гука определяется самостоятельно. Для эксперимента потребуется пружина, линейка, груз с определённой массой. Необходимо соблюдать следующую последовательность действий:
- Пружина фиксируется вертикально. Для этого используется любая удобная опора со свободной нижней частью.
- Линейкой измеряется длина предмета. Результат записывается как х1.
- На свободный конец подвешивается груз с известной массой m.
- Измеряется длина изделия под воздействием амплитуды. Вывод записывается как х2.
- Производит подсчёт абсолютного удлинения: x = x2-x1. Для определения энергии (силы) и k в международной системе СИ осуществляется перевод длины из разных единиц измерения в метры.
- Сила, спровоцировавшая деформацию, считается силой тяжести тела. Она рассчитывается по формуле: F = mg, где м является массой используемого груза (вес переводится в килограммы), а g (равен 9,8) — постоянная величина, с помощью которой отмечается ускорение свободного падения.
Если вышеописанные вычисления произведены, необходимо найти значение коэффициента жёсткости. Используется закон Гука, из которого следует, что k=F/x.
Решение задач
Для нахождения жёсткости в случае использования разных предметов, включая пружинные маятники с разной частотой колебаний, применяется формула Гука либо следствие, вытекающее из неё.
Задача № 1. Пружина имеет длину 10 см. На неё оказывается сила в 100 Н. Изделие растянулось на 14 см. Нужно найти k.
Решение: предварительно вычисляется абсолютное удлинение: 14−10=4 см. Результат переводится в метры: 0,04 м. Используя основную формулу, находится k. Его значение равняется 2500 Н/м.
Задача № 2. На пружину подвешивается груз массой 10 кг. Изделие растягивается на 4 см. Нужно найти длину, на которую растянется пружина, если использовать груз массой в 25 кг.
Решение: Определяется сила тяжести путем умножения 10 кг на 9.8. Результат записывается в Ньютонах. Определяется k=98/0.04=2450 Н/м. Рассчитывается, с какой силой воздействует второй груз: F=mg=245 Н. Для нахождения абсолютного удлинения используется формула x=F/k. Во втором случае х равняется 0,1 м.
Применение цилиндрических пружин
На производстве наиболее востребованы цилиндрические пружины, так как они обладают уникальными особенностями. При создании системы отмечается центральная ось, вдоль которой действуют разные силы. В процессе изготовления подобных изделий используется проволока соответствующего диаметра.
Для её изготовления понадобится специальный сплав либо обычные металлы. Сам материал должен обладать высокой упругостью. Проволока может иметь витки одного диаметра либо разных радиусов. Большим спросом пользуются цилиндрическая пружина, которая в сжатом состоянии обладает незначительной толщиной.
Главными параметрами изделия считаются:
- малый, средний и большой диаметр витков и самой проволоки;
- шаг размещения отдельный колец.
В задачах по физике вычисляется k для двух состояний: растяжение и сжатие. В любом случае используется одна формула для определения величины. Разница понятий:
- Исполнение, рассчитанное на сжатие, характеризуется дальним размещением витков. Расстояние, образуемое между ними, появляется возможность на сжатие.
- Модель, связанная с растяжением, имеет кольца, расположенные плотно между собой. Такая форма определяет то, что при максимальной силе растяжение минимальное.
Отдельно рассматриваются варианты на изгиб и кручение. Такие детали рассчитываются по специальным формулам. Для разных соединений характерны определённые особенности. Чтобы провести определения растяжения, учитывается момент теста.
Показатель зависит от характеристик проволоки, оказываемой силы либо массы тела. Для всех систем используются разные формулы, но полученные результаты не имеют погрешностей. Чтобы провести тесты для вычисления основных параметров, используется специальное оборудование. Простые задачи с деформацией пружин решают ученики на уроках физике в 7−8 классе. О параллельном и последовательном соединении элементов системы узнают учащиеся старших классов.
Определение
Жесткость — способность твёрдого тела, конструкции или её элементов сопротивляться деформации от приложенного усилия вдоль выбранного направления в заданной системе координат.
Сила жесткости — сила, возникающая в теле в результате его деформации и стремящаяся вернуть его в исходное состояние.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
От чего зависит жесткость
Жесткость пружины зависит от нескольких параметров:
- геометрии пружины;
- типа материала;
- коэффициента;
- срока эксплуатации.
Геометрия пружины
На жесткость витой пружины влияет:
- количество витков;
- их диаметр;
- диаметр проволоки.
Диаметр намотки измеряется от оси пружины. Так как длина проволоки в пружине значительно больше длины упругого стержня, сопротивляемость внешней деформации многократно возрастает.
Волновые пружины состоят из металлических лент, навитых ребром по окружности заданного диаметра.
Их основные геометрические параметры:
- количество витков;
- количество волн на виток;
- сечение ленты.
Тип материала
У каждого материала есть условный предел упругости, характеризующий его способность восстанавливаться после деформации. Если этот предел превышается, в структуре материала возникают необратимые изменения.
Определение
Предел упругости — механическая характеристика материала, показывающая максимальное напряжение, при котором имеют место только упругие, обратимые деформации.
Предел упругости измеряют в паскалях и определяют по формуле:
(sigma_{у;}=;frac FS)
где F — действие внешней силы на исследуемый образец, приводящее к повреждениям, а S — его площадь.
Кроме предела упругости, существуют такие характеристики упругости материалов, как модули упругости (модуль Юнга) и сдвига, коэффициент жесткости и другие. Все они взаимосвязаны, поэтому, выяснив значение одной из величин с помощью справочной таблицы, можно вычислить другие.
Коэффициент
Определение
Согласно закону Гука, при малой деформации абсолютная величина силы упругости прямо пропорциональна величине деформации.
Эта линейная зависимость описывается формулой:
(F=;k;times;x)
где k — коэффициент жесткости, а х — величина, на которую сжалась или растянулась пружина.
Примечание
Деформация считается малой в том случае, когда изменение размеров тела значительно меньше его первоначальных размеров.
Срок эксплуатации
Нахождение под напряжением приводит к постепенной необратимой деформации, называемой ослаблением пружины.
Жесткость пружины влияет на срок ее эксплуатации, как и сила воздействия. Конструкторы пружин, предварительно рассчитав эти параметры, проводят тесты на прототипах, прежде чем начать массовое производство. В специальных установках для испытания на усталость материала их сжимают и отпускают определенное количество циклов, отдельно проверяя поведение пружин при максимальной и минимальной нагрузке.
В чем измеряется жесткость
Жесткость пружины в системе СИ измеряется в ньютонах на метр, Н/м. Также встречается единица измерения ньютон на миллиметр, Н/мм. Численно жесткость равна величине силы, изменяющей размер пружины на метр длины.
Как обозначается
Коэффициент жесткости пружины обозначают буквой k.
Коэффициент жесткости пружины
Определение
Коэффициент жесткости — коэффициент, связывающий в законе Гука удлинение упругого тела и возникающую вследствие этого удлинения силу жесткости.
Применяется в механике твердого тела в разделе упругости.
Формула расчета через массу и длину
Используя закон Гука, коэффициент жесткости можно вычислить по формуле:
(k;=;frac Fx)
Чтобы выяснить силу тяжести, воздействующую на пружину, нужно воспользоваться формулой:
(F;=;m;times;g)
где m — масса подвешенного на пружине тела, а g — величина свободного ускорения, равная 9,8.
Чтобы найти х, нужно дважды измерить длину пружины и вычислить разницу между этими двумя значениями.
При соединении нескольких пружин общая жесткость системы меняется. Коэффициенты каждой из пружин суммируются при параллельном соединении. При последовательном соединении общая жесткость вычисляется по формуле:
(frac1k;=;(frac1{k_1};+;frac1{k_2};+;…;+;frac1{k_n}))
Как можно измерить жесткость
Измерительные приборы
Приборы для испытания пружин на сжатие-растяжение контролируют приложенное усилие с помощью тензометрического датчика, а также изменение их длины, выводя показатели на дисплей. Без специального прибора измерить осевую жесткость можно, используя динамометр и линейку.
Существуют приборы и для измерения поперечной жесткости пружин. Для этого нужно измерить смещение нескольких точек пружины, определив расстояние и угол между ними.
Практическая задача
Самый простой способ измерить жесткость пружины — провести стандартный школьный опыт со штативом и подвешенными на пружине грузиками.
Для измерения осевой жесткости спиральной пружины используют:
- штатив, на котором закрепляют пружину;
- крючок, который крепят на свободный ее конец;
- грузики с известной массой, которые подвешивают на свободный конец пружины;
- линейку, чтобы измерить длину пружины с грузом и без груза.
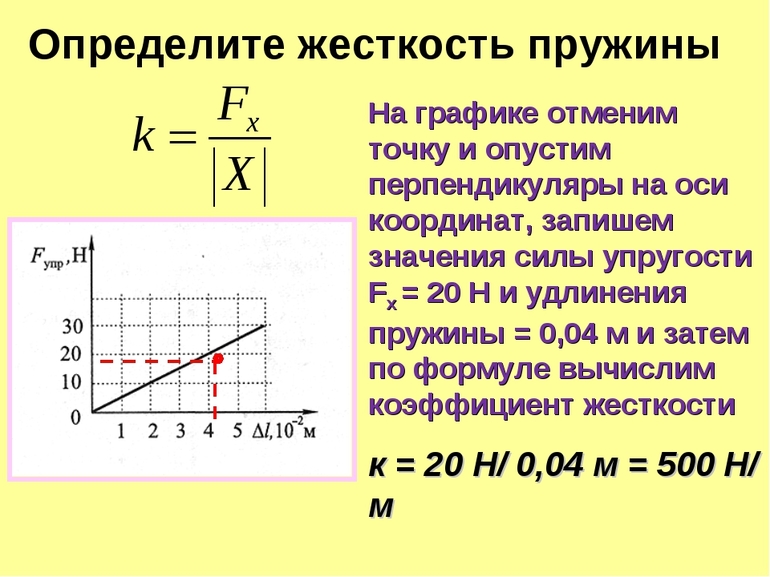
Проведя несколько измерений с грузиками разной массы и вычислив силу тяжести, воздействовавшую на пружину в каждом из них, можно построить график зависимости длины пружины от приложенного усилия и узнать среднее значение коэффициента жесткости.
Альтернативные способы определения жесткости
Жесткость пружины можно определить и через период ее колебания, воспользовавшись формулой:
(Т;=;2mathrmpisqrt{frac{mathrm m}{mathrm k}})
Или через частоту колебаний по формуле:
(omega=;sqrt{frac{mathrm k}{mathrm m}})
Проводя опыт с пружиной, закрепленной на штативе, и грузиками с известной массой, можно не измерять длину пружины, а привести ее в колебательное движение и сосчитать количество колебаний в период времени.
Формула расчета через длину, дающая более точные результаты и применимая к пружинам со значительной деформацией, различается для пружин разных геометрических параметров. Например, жесткость витой цилиндрической пружины, упруго деформируемой вдоль оси, вычисляется по формуле:
(k=;frac{d_D^4;times;G}{8;times;d_F^3;times;n})
где (d_D) — диаметр проволоки, (d_F) — диаметр намотки, (G) — модуль сдвига, который зависит от материала, а (n) — число витков.
Задача
Рассчитайте коэффициент жесткости пружины, если известно, что ее диаметр 20 мм, диаметр проволоки 1 мм, число витков — 25. Модуль сдвига равен (8times;10^{10};) Па.
Решение
Переведем числовые значения в систему СИ и подставим в формулу:
(k;=;frac{{(10^{-3})}^{4;}times8;times;10^{10}}{8;times;left(2;times;10^{-2}right)^3;times;25})
(k = 100 frac Нм)
Жесткость при деформации кручения существенно отличается от жесткости сжатия-растяжения. Предел прочности при кручении у любого материала будет меньше, чем предел прочности при сжатии-растяжении или изгибе. Торсионная жесткость, также называемая крутильной, в системе СИ измеряется в ньютон-метрах на радиан, сокращенно Н-м/рад. Ее можно определить по формуле:
(k;=;frac Malpha)
где (М) — крутящий момент, приложенный к телу, а (alpha) — угол закручивания тела по оси приложения крутящего момента.
Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?
Содержание:
- Сила упругости и закон Гука
- Определение коэффициента жесткости
- Расчет жесткости системы
- Последовательное соединение системы пружин
- Параллельное соединение системы пружин
- Вычисление коэффициента жесткости опытным методом
- Примеры задач на нахождение жесткости
- Видео
Сила упругости и закон Гука
Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.
Примерами пластических деформаций являются:
- лепка из глины;
- погнутая алюминиевая ложка.
В свою очередь, упругими деформациями будут считаться:
- резинка (можно растянуть ее, после чего она вернется в исходное состояние);
- пружина (после сжатия снова распрямляется).
В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:
F = — k·x;
где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).
Определение коэффициента жесткости
Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:
k = F/x.
Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.
Единица измерения жесткости в СИ — Н/м.
Расчет жесткости системы
Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.
Последовательное соединение системы пружин
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
1/k = 1/k1 + 1/k2 + … + 1/ki,
где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.
Параллельное соединение системы пружин
В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
k = k1 + k2 + … + ki.
Измерение жесткости пружины опытным путем — в этом видео.
Вычисление коэффициента жесткости опытным методом
С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:
- линейка;
- пружина;
- груз с известной массой.
Последовательность действий для опыта такова:
- Необходимо закрепить пружину вертикально, подвесив ее к любой удобной опоре. Нижний край должен остаться свободным.
- При помощи линейки измеряется ее длина и записывается как величина x1.
- На свободный конец нужно подвесить груз с известной массой m.
- Длина пружины измеряется в нагруженном состоянии. Обозначается величиной x2.
- Подсчитывается абсолютное удлинение: x = x2-x1. Для того чтобы получить результат в международной системе единиц, лучше сразу перевести его из сантиметров или миллиметров в метры.
- Сила, которая вызвала деформацию, — это сила тяжести тела. Формула для ее расчета — F = mg, где m — это масса используемого в эксперименте груза (переводится в кг), а g — величина свободного ускорения, равная приблизительно 9,8.
- После проведенных расчетов остается найти только сам коэффициент жесткости, формула которого была указана выше: k = F/x.
Примеры задач на нахождение жесткости
Задача 1
На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.
- Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
- По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.
Ответ: жесткость пружины составит 2500 Н/м.
Задача 2
Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.
- Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
- Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
- Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
- По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
- Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.
Ответ: во втором случае пружина растянется на 10 см.
Видео
Из этого видео вы узнаете, как определить жесткость пружины.
На чтение 6 мин Просмотров 1.5к.
При внешнем воздействии тело ускоряется либо деформируется. Последнее явление проявляется изменением форм или размеров. Если объект восстанавливается в покое на 100%, деформация называется упругой (резинка), а в остальных случаях — пластической (лепка изделий из глины). Для вычисления первого показателя используется формула жесткости пружины (F = k · x).
Трактовка понятий
В физике упругая деформация возникает из-за силы, равной по модулю оказываемому воздействию. Сила упругости для пружины (F) пропорциональна её удлинению. Для определения жесткости пружины зависимость записывается математически с помощью следующей формулы: F = k·x; где х — длина предмета после его растяжения, а k — коэффициент жесткости.
Формула считается частным случаем закона Гука, который используется для растяжимого тонкого стержня. Чрезмерное воздействие приводит к появлению разных дефектов. Для процесса характерны некоторые особенности, от чего зависит жесткость пружины:
- геометрические параметры детали;
- срок эксплуатации;
- значение коэффициента k, который при определённых условиях способствует снижению сжатия и сохранению силы на одинаковом уровне;
- тип используемого материала (сталь, сплав) в процессе изготовления пружины.
На практических занятиях по физике в 7 классе применяются изделия разных типов. В автомобилестроении используется цветовое обозначение. Для расчета коэффициента жесткости пружины специалисты ориентируются на формулу k=Gd 4 /8D 3 n, где:
- G — определяет модуль сдвига (свойство зависит, к примеру, от используемого сырья);
- d — диаметр куска проволоки (величина определяется в период производства путём проката, а результат записывается в технической документации);
- D — диаметр витков, которые получаются в результате намотки на проволоку (расчет осуществляется с учетом поставленных задач и зависит от нагрузки, оказываемой для сжатия объекта);
- n — количество витков в системе (показатель варьируется в значительном диапазоне, от чего зависят эксплуатационные характеристики предмета).
С помощью формулы может измеряться жёсткость цилиндрической пружины, используемой в разных механизмах. Показатель измеряется в Ньютонах и обозначается Н.
Практические занятия
Механики и физики обозначают с помощью k, c и D коэффициент упругости, пропорциональности, жесткости. Смысл математической записи одинаковый. Численно показатель равняется силе, которая создаёт колебания на одну единицу длины. На практических работах по физике используется в качестве последней величины 1 метр.
Чем выше k, тем больше сопротивление предмета относительно деформации. Дополнительно коэффициент показывает степень устойчивости тела к колебаниям со стороны внешней нагрузки. Параметр зависит от длины и диаметра винтового изделия, количества витков, сырья. Единица измерения жесткости пружины — Н/м.
На практике перед школьниками и механиками может стоять более сложная задача, к примеру, найти общую жёсткость. В таком случае пружины соединены последовательным либо параллельным способом. В первом случае уменьшается суммарная жесткость. Если пружины расположены последовательно, используется следующая формула: 1/k = 1/k1 + 1/k2 + … + 1/ki, где:
- k — суммарная жёсткость соединений;
- k1 …ki — жёсткость каждого элемента системы;
- i — число пружин в цепи.
Если невесомые (расположены горизонтально) предметы соединены параллельно, значение общего k будет увеличиваться. Величина вычисляется по следующей формуле: k = k1 + k2 + … + ki.
Основная методика для вычислений
На практике коэффициент Гука определяется самостоятельно. Для эксперимента потребуется пружина, линейка, груз с определённой массой. Необходимо соблюдать следующую последовательность действий:
Если вышеописанные вычисления произведены, необходимо найти значение коэффициента жёсткости. Используется закон Гука, из которого следует, что k=F/x.
Решение задач
Для нахождения жёсткости в случае использования разных предметов, включая пружинные маятники с разной частотой колебаний, применяется формула Гука либо следствие, вытекающее из неё.
Задача № 1. Пружина имеет длину 10 см. На неё оказывается сила в 100 Н. Изделие растянулось на 14 см. Нужно найти k.
Решение: предварительно вычисляется абсолютное удлинение: 14−10=4 см. Результат переводится в метры: 0,04 м. Используя основную формулу, находится k. Его значение равняется 2500 Н/м.
Задача № 2. На пружину подвешивается груз массой 10 кг. Изделие растягивается на 4 см. Нужно найти длину, на которую растянется пружина, если использовать груз массой в 25 кг.
Решение: Определяется сила тяжести путем умножения 10 кг на 9.8. Результат записывается в Ньютонах. Определяется k=98/0.04=2450 Н/м. Рассчитывается, с какой силой воздействует второй груз: F=mg=245 Н. Для нахождения абсолютного удлинения используется формула x=F/k. Во втором случае х равняется 0,1 м.
Применение цилиндрических пружин
На производстве наиболее востребованы цилиндрические пружины, так как они обладают уникальными особенностями. При создании системы отмечается центральная ось, вдоль которой действуют разные силы. В процессе изготовления подобных изделий используется проволока соответствующего диаметра.
Для её изготовления понадобится специальный сплав либо обычные металлы. Сам материал должен обладать высокой упругостью. Проволока может иметь витки одного диаметра либо разных радиусов. Большим спросом пользуются цилиндрическая пружина, которая в сжатом состоянии обладает незначительной толщиной.
Главными параметрами изделия считаются:
- малый, средний и большой диаметр витков и самой проволоки;
- шаг размещения отдельный колец.
В задачах по физике вычисляется k для двух состояний: растяжение и сжатие. В любом случае используется одна формула для определения величины. Разница понятий:
Отдельно рассматриваются варианты на изгиб и кручение. Такие детали рассчитываются по специальным формулам. Для разных соединений характерны определённые особенности. Чтобы провести определения растяжения, учитывается момент теста.
Показатель зависит от характеристик проволоки, оказываемой силы либо массы тела. Для всех систем используются разные формулы, но полученные результаты не имеют погрешностей. Чтобы провести тесты для вычисления основных параметров, используется специальное оборудование. Простые задачи с деформацией пружин решают ученики на уроках физике в 7−8 классе. О параллельном и последовательном соединении элементов системы узнают учащиеся старших классов.
Формула жесткости пружины в физике
Формула жесткости пружины
Определение и формула жесткости пружины
Определение
Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости.
Чаще всего ее обозначают ${overline{F}}_{upr}$. Сила упругости появляется только при деформации тела и исчезает, если пропадает деформация. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.
Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.
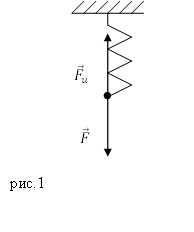
Рассмотрим пружину, на которую действует растягивающая сила ($overline{F}$), которая направлена вертикально вниз (рис.1).
Силу $overline{F }$ назовем деформирующей силой. От воздействия деформирующей силы длина пружины увеличивается. В результате в пружине появляется сила упругости (${overline{F}}_u$), уравновешивающая силу $overline{F }$. Если деформация является небольшой и упругой, то удлинение пружины ($Delta l$) прямо пропорционально деформирующей силе:
[overline{F}=kDelta lleft(1right),]
где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) $k$.
Жесткость (как свойство) — это характеристика упругих свойств тела, которое деформируют. Жесткость считают возможностью тела оказать противодействие внешней силе, способность сохранять свои геометрические параметры. Чем больше жесткость пружины, тем меньше она изменяет свою длину под воздействием заданной силы. Коэффициент жесткости — это основная характеристика жесткости (как свойства тела).
Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:
[k=frac{Gd^4}{8d^3_pn}left(2right),]
где $G$ — модуль сдвига (величина, зависящая от материала); $d$ — диаметр проволоки; $d_p$ — диаметр витка пружины; $n$ — количество витков пружины.
Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:
[left[kright]=left[frac{F_{upr }}{x}right]=frac{left[F_{upr }right]}{left[xright]}=frac{Н}{м}.]
Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.
Формула жесткости соединений пружин
Пусть $N$ пружин соединены последовательно. Тогда жесткость всего соединения равна:
[frac{1}{k}=frac{1}{k_1}+frac{1}{k_2}+dots =sumlimits^N_{ i=1}{frac{1}{k_i}left(3right),}]
где $k_i$ — жесткость $i-ой$ пружины.
При последовательном соединении пружин жесткость системы определяют как:
[k=k_1+k_2+dots +sumlimits^N_{i=1}{k_i}left(4right).]
Примеры задач с решением
Пример 1
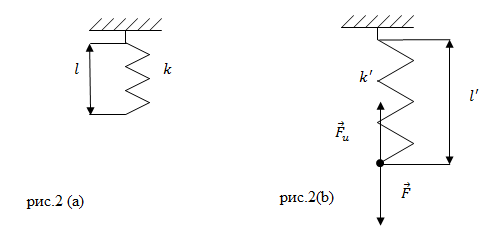
Задание. Пружина в отсутствии нагрузки имеет длину $l=0,01$ м и жесткость равную 10 $frac{Н}{м}. $Чему будет равна жесткость пружины и ее длина, если на пружину действовать силой $F$= 2 Н? Считайте деформацию пружины малой и упругой.
Решение. Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:
[k=k’left(1.1right).]
При упругих деформациях выполняется закон Гука:
[F=kDelta l left(1.2right).]
Из (1.2) найдем удлинение пружины:
[Delta l=frac{F}{k}left(1.3right).]
Длина растянутой пружины равна:
[l’=l+Delta l=l+frac{F}{k}.]
Вычислим новую длину пружины:
[l’=0,01+frac{2}{10}=0,21 left(мright).]
Ответ. 1) $k’=10 frac{Н}{м}$; 2) $l’=0,21$ м
Пример 2
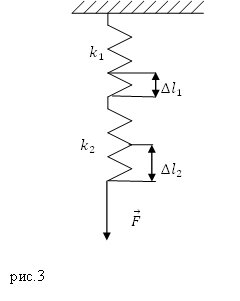
Задание. Две пружины, имеющие жесткости $k_1$ и $k_2$ соединили последовательно. Какой будет удлинение первой пружины (рис.3), если длина второй пружины увеличилась на величину $Delta l_2$?
Решение. Если пружины соединены последовательно, то деформирующая сила ($overline{F}$), действующая на каждую из пружин одинакова, то есть можно записать для первой пружины:
[F=k_1Delta l_1left(2.1right).]
Для второй пружины запишем:
[F=k_2Delta l_2left(2.2right).]
Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:
[k_1Delta l_1=k_2Delta l_2left(2.3right).]
Из равенства (2.3) получим удлинение первой пружины:
[Delta l_1=frac{k_2Delta l_2}{k_1}.]
Ответ. $Delta l_1=frac{k_2Delta l_2}{k_1}$
Читать дальше: формула закона Архимеда.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
For pain and/or loss of range of motion of a joint, see joint stiffness. For the term regarding the stability of a differential equation, see stiff equation.
Extension of a coil spring, 
Stiffness is the extent to which an object resists deformation in response to an applied force.[1]
The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is.[2]
Calculations[edit]
The stiffness, 
where,
In the International System of Units, stiffness is typically measured in newtons per meter (
Generally speaking, deflections (or motions) of an infinitesimal element (which is viewed as a point) in an elastic body can occur along multiple DOF (maximum of six DOF at a point). For example, a point on a horizontal beam can undergo both a vertical displacement and a rotation relative to its undeformed axis. When there are 

It is noted that for a body with multiple DOF, the equation above generally does not apply since the applied force generates not only the deflection along its direction (or degree of freedom) but also those along with other directions.
For a body with multiple DOF, to calculate a particular direct-related stiffness (the diagonal terms), the corresponding DOF is left free while the remaining should be constrained. Under such a condition, the above equation can obtain the direct-related stiffness for the degree of unconstrained freedom. The ratios between the reaction forces (or moments) and the produced deflection are the coupling stiffnesses.
The elasticity tensor describes all possible stretch and shear parameters is given by the elasticity tensor.
Compliance[edit]
The inverse of stiffness is flexibility or compliance, typically measured in units of metres per newton. In rheology, it may be defined as the ratio of strain to stress,[3] and so take the units of reciprocal stress, for example, 1/Pa.
Rotational stiffness[edit]
Twist, by angle 

A body may also have a rotational stiffness, 
where
In the SI system, rotational stiffness is typically measured in newton-metres per radian.
In the SAE system, rotational stiffness is typically measured in inch-pounds per degree.
Further measures of stiffness are derived on a similar basis, including:
- shear stiffness — the ratio of applied shear force to shear deformation
- torsional stiffness — the ratio of applied torsion moment to the angle of twist
Relationship to elasticity[edit]
The elastic modulus of a material is not the same as the stiffness of a component made from that material. Elastic modulus is a property of the constituent material; stiffness is a property of a structure or component of a structure, and hence it is dependent upon various physical dimensions that describe that component. That is, the modulus is an intensive property of the material; stiffness, on the other hand, is an extensive property of the solid body that is dependent on the material and its shape and boundary conditions. For example, for an element in tension or compression, the axial stiffness is
where
Similarly, the torsional stiffness of a straight section is
where
Note that the torsional stiffness has dimensions [force] * [length] / [angle], so that its SI units are N*m/rad.
For the special case of unconstrained uniaxial tension or compression, Young’s modulus can be thought of as a measure of the stiffness of a structure.
Applications[edit]
The stiffness of a structure is of principal importance in many engineering applications, so the modulus of elasticity is often one of the primary properties considered when selecting a material. A high modulus of elasticity is sought when deflection is undesirable, while a low modulus of elasticity is required when flexibility is needed.
In biology, the stiffness of the extracellular matrix is important for guiding the migration of cells in a phenomenon called durotaxis.
Another application of stiffness finds itself in skin biology. The skin maintains its structure due to its intrinsic tension, contributed to by collagen, an extracellular protein that accounts for approximately 75% of its dry weight.[4] The pliability of skin is a parameter of interest that represents its firmness and extensibility, encompassing characteristics such as elasticity, stiffness, and adherence. These factors are of functional significance to patients.[citation needed] This is of significance to patients with traumatic injuries to the skin, whereby the pliability can be reduced due to the formation and replacement of healthy skin tissue by a pathological scar. This can be evaluated both subjectively, or objectively using a device such as the Cutometer. The Cutometer applies a vacuum to the skin and measures the extent to which it can be vertically distended. These measurements are able to distinguish between healthy skin, normal scarring, and pathological scarring,[5] and the method has been applied within clinical and industrial settings to monitor both pathophysiological sequelae, and the effects of treatments on skin.
See also[edit]
- Bending stiffness
- Compliant mechanism – Mechanism which transmits force through elastic body deformation
- Elasticity (physics) – Physical property when materials or objects return to original shape after deformation
- Elastic modulus – Physical property that measures stiffness of material
- Elastography – Any of several imaging modalities that map degrees of soft-tissue elasticity and stiffness
- Hardness – Measure of a material’s resistance to localized plastic deformation
- Hooke’s law – Physical law: force needed to deform a spring scales linearly with distance
- Mechanical impedance – Relationship between harmonic force and velocity
- Moment of inertia – Scalar measure of the rotational inertia with respect to a fixed axis of rotation
- Shore durometer
- Spring (device) – Elastic object that stores mechanical energy
- Stiffness (mathematics)
- Stiffness tensor
- Young’s modulus – Mechanical property that measures stiffness of a solid material
References[edit]
- ^ Baumgart F. (2000). «Stiffness—an unknown world of mechanical science?». Injury. Elsevier. 31: 14–84. doi:10.1016/S0020-1383(00)80040-6.
“Stiffness” = “Load” divided by “Deformation”
- ^ Martin Wenham (2001), «Stiffness and flexibility», 200 science investigations for young students, p. 126, ISBN 978-0-7619-6349-3
- ^ V. GOPALAKRISHNAN and CHARLES F. ZUKOSKI; «Delayed flow in thermo-reversible colloidal gels»; Journal of Rheology; Society of Rheology, U.S.A.; July/August 2007; 51 (4): pp. 623–644.
- ^ Chattopadhyay, S.; Raines, R. (August 2014). «Collagen-Based Biomaterials for Wound Healing». Biopolymers. 101 (8): 821–833. doi:10.1002/bip.22486. PMC 4203321. PMID 24633807.
- ^ Nedelec, Bernadette; Correa, José; de Oliveira, Ana; LaSalle, Leo; Perrault, Isabelle (2014). «Longitudinal burn scar quantification». Burns. 40 (8): 1504–1512. doi:10.1016/j.burns.2014.03.002. PMID 24703337.
For pain and/or loss of range of motion of a joint, see joint stiffness. For the term regarding the stability of a differential equation, see stiff equation.
Extension of a coil spring, 
Stiffness is the extent to which an object resists deformation in response to an applied force.[1]
The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is.[2]
Calculations[edit]
The stiffness, 
where,
In the International System of Units, stiffness is typically measured in newtons per meter (
Generally speaking, deflections (or motions) of an infinitesimal element (which is viewed as a point) in an elastic body can occur along multiple DOF (maximum of six DOF at a point). For example, a point on a horizontal beam can undergo both a vertical displacement and a rotation relative to its undeformed axis. When there are 

It is noted that for a body with multiple DOF, the equation above generally does not apply since the applied force generates not only the deflection along its direction (or degree of freedom) but also those along with other directions.
For a body with multiple DOF, to calculate a particular direct-related stiffness (the diagonal terms), the corresponding DOF is left free while the remaining should be constrained. Under such a condition, the above equation can obtain the direct-related stiffness for the degree of unconstrained freedom. The ratios between the reaction forces (or moments) and the produced deflection are the coupling stiffnesses.
The elasticity tensor describes all possible stretch and shear parameters is given by the elasticity tensor.
Compliance[edit]
The inverse of stiffness is flexibility or compliance, typically measured in units of metres per newton. In rheology, it may be defined as the ratio of strain to stress,[3] and so take the units of reciprocal stress, for example, 1/Pa.
Rotational stiffness[edit]
Twist, by angle 

A body may also have a rotational stiffness, 
where
In the SI system, rotational stiffness is typically measured in newton-metres per radian.
In the SAE system, rotational stiffness is typically measured in inch-pounds per degree.
Further measures of stiffness are derived on a similar basis, including:
- shear stiffness — the ratio of applied shear force to shear deformation
- torsional stiffness — the ratio of applied torsion moment to the angle of twist
Relationship to elasticity[edit]
The elastic modulus of a material is not the same as the stiffness of a component made from that material. Elastic modulus is a property of the constituent material; stiffness is a property of a structure or component of a structure, and hence it is dependent upon various physical dimensions that describe that component. That is, the modulus is an intensive property of the material; stiffness, on the other hand, is an extensive property of the solid body that is dependent on the material and its shape and boundary conditions. For example, for an element in tension or compression, the axial stiffness is
where
Similarly, the torsional stiffness of a straight section is
where
Note that the torsional stiffness has dimensions [force] * [length] / [angle], so that its SI units are N*m/rad.
For the special case of unconstrained uniaxial tension or compression, Young’s modulus can be thought of as a measure of the stiffness of a structure.
Applications[edit]
The stiffness of a structure is of principal importance in many engineering applications, so the modulus of elasticity is often one of the primary properties considered when selecting a material. A high modulus of elasticity is sought when deflection is undesirable, while a low modulus of elasticity is required when flexibility is needed.
In biology, the stiffness of the extracellular matrix is important for guiding the migration of cells in a phenomenon called durotaxis.
Another application of stiffness finds itself in skin biology. The skin maintains its structure due to its intrinsic tension, contributed to by collagen, an extracellular protein that accounts for approximately 75% of its dry weight.[4] The pliability of skin is a parameter of interest that represents its firmness and extensibility, encompassing characteristics such as elasticity, stiffness, and adherence. These factors are of functional significance to patients.[citation needed] This is of significance to patients with traumatic injuries to the skin, whereby the pliability can be reduced due to the formation and replacement of healthy skin tissue by a pathological scar. This can be evaluated both subjectively, or objectively using a device such as the Cutometer. The Cutometer applies a vacuum to the skin and measures the extent to which it can be vertically distended. These measurements are able to distinguish between healthy skin, normal scarring, and pathological scarring,[5] and the method has been applied within clinical and industrial settings to monitor both pathophysiological sequelae, and the effects of treatments on skin.
See also[edit]
- Bending stiffness
- Compliant mechanism – Mechanism which transmits force through elastic body deformation
- Elasticity (physics) – Physical property when materials or objects return to original shape after deformation
- Elastic modulus – Physical property that measures stiffness of material
- Elastography – Any of several imaging modalities that map degrees of soft-tissue elasticity and stiffness
- Hardness – Measure of a material’s resistance to localized plastic deformation
- Hooke’s law – Physical law: force needed to deform a spring scales linearly with distance
- Mechanical impedance – Relationship between harmonic force and velocity
- Moment of inertia – Scalar measure of the rotational inertia with respect to a fixed axis of rotation
- Shore durometer
- Spring (device) – Elastic object that stores mechanical energy
- Stiffness (mathematics)
- Stiffness tensor
- Young’s modulus – Mechanical property that measures stiffness of a solid material
References[edit]
- ^ Baumgart F. (2000). «Stiffness—an unknown world of mechanical science?». Injury. Elsevier. 31: 14–84. doi:10.1016/S0020-1383(00)80040-6.
“Stiffness” = “Load” divided by “Deformation”
- ^ Martin Wenham (2001), «Stiffness and flexibility», 200 science investigations for young students, p. 126, ISBN 978-0-7619-6349-3
- ^ V. GOPALAKRISHNAN and CHARLES F. ZUKOSKI; «Delayed flow in thermo-reversible colloidal gels»; Journal of Rheology; Society of Rheology, U.S.A.; July/August 2007; 51 (4): pp. 623–644.
- ^ Chattopadhyay, S.; Raines, R. (August 2014). «Collagen-Based Biomaterials for Wound Healing». Biopolymers. 101 (8): 821–833. doi:10.1002/bip.22486. PMC 4203321. PMID 24633807.
- ^ Nedelec, Bernadette; Correa, José; de Oliveira, Ana; LaSalle, Leo; Perrault, Isabelle (2014). «Longitudinal burn scar quantification». Burns. 40 (8): 1504–1512. doi:10.1016/j.burns.2014.03.002. PMID 24703337.