Как пишется знак бесконечности на бумаге

Infinity symbol
In Unicode	U+221E ∞ INFINITY (∞)
Different from
Different from	U+267E ♾ PERMANENT PAPER SIGN U+26AD ⚭ MARRIAGE SYMBOL

The infinity symbol () is a mathematical symbol representing the concept of infinity. This symbol is also called a lemniscate,^[1] after the lemniscate curves of a similar shape studied in algebraic geometry,^[2] or «lazy eight», in the terminology of livestock branding.^[3]

This symbol was first used mathematically by John Wallis in the 17th century, although it has a longer history of other uses. In mathematics, it often refers to infinite processes (potential infinity) rather than infinite values (actual infinity). It has other related technical meanings, such as the use of long-lasting paper in bookbinding, and has been used for its symbolic value of the infinite in modern mysticism and literature. It is a common element of graphic design, for instance in corporate logos as well as in older designs such as the Métis flag.

Both the infinity symbol itself and several variations of the symbol are available in various character encodings.

History[edit]

The lemniscate has been a common decorative motif since ancient times; for instance it is commonly seen on Viking Age combs.^[4]

The English mathematician John Wallis is credited with introducing the infinity symbol with its mathematical meaning in 1655, in his De sectionibus conicis.^[5][6][7] Wallis did not explain his choice of this symbol. It has been conjectured to be a variant form of a Roman numeral, but which Roman numeral is unclear. One theory proposes that the infinity symbol was based on the numeral for 100 million, which resembled the same symbol enclosed within a rectangular frame.^[8] Another proposes instead that it was based on the notation CIↃ used to represent 1,000.^[9] Instead of a Roman numeral, it may alternatively be derived from a variant of ω, the lower-case form of omega, the last letter in the Greek alphabet.^[9]

Perhaps in some cases because of typographic limitations, other symbols resembling the infinity sign have been used for the same meaning.^[7] Leonhard Euler used an open letterform more closely resembling a reflected and sideways S than a lemniscate,^[10] and even «O–O» has been used as a stand-in for the infinity symbol itself.^[7]

Usage[edit]

Mathematics[edit]

In mathematics, the infinity symbol is used more often to represent a potential infinity,^[11] rather than an actually infinite quantity as included in the extended real numbers, the cardinal numbers and the ordinal numbers (which use other notations, such as and ω, for infinite values). For instance, in mathematical expressions with summations and limits such as

the infinity sign is conventionally interpreted as meaning that the variable grows arbitrarily large towards infinity, rather than actually taking an infinite value, although other interpretations are possible.^[12]

The infinity symbol may also be used to represent a point at infinity, especially when there is only one such point under consideration. This usage includes, in particular, the infinite point of a projective line,^[13] and the point added to a topological space to form its one-point compactification.^[14]

Other technical uses[edit]

In areas other than mathematics, the infinity symbol may take on other related meanings. For instance, it has been used in bookbinding to indicate that a book is printed on acid-free paper and will therefore be long-lasting.^[15] On cameras and their lenses, the infinity symbol indicates that the lens’s focal length is set to an infinite distance, and is «probably one of the oldest symbols to be used on cameras».^[16]

Symbolism and literary uses[edit]

In modern mysticism, the infinity symbol has become identified with a variation of the ouroboros, an ancient image of a snake eating its own tail that has also come to symbolize the infinite, and the ouroboros is sometimes drawn in figure-eight form to reflect this identification—rather than in its more traditional circular form.^[18]

In the works of Vladimir Nabokov, including The Gift and Pale Fire, the figure-eight shape is used symbolically to refer to the Möbius strip and the infinite, as is the case in these books’ descriptions of the shapes of bicycle tire tracks and of the outlines of half-remembered people. Nabokov’s poem after which he entitled Pale Fire explicitly refers to «the miracle of the lemniscate».^[19] Other authors whose works use this shape with its symbolic meaning of the infinite include James Joyce, in Ulysses,^[20] and David Foster Wallace, in Infinite Jest.^[21]

Graphic design[edit]

The well-known shape and meaning of the infinity symbol have made it a common typographic element of graphic design. For instance, the Métis flag, used by the Canadian Métis people since the early 19th century, is based around this symbol.^[22] Different theories have been put forward for the meaning of the symbol on this flag, including the hope for an infinite future for Métis culture and its mix of European and First Nations traditions,^[23][24] but also evoking the geometric shapes of Métic dances,^[25], Celtic knots,^[26] or Plains First Nations Sign Language.^[27]

A rainbow-coloured infinity symbol is also used by the neurodiversity movement, as a way to symbolize the infinite variation of the people in the movement and of human cognition.^[28] The Bakelite company took up this symbol in its corporate logo to refer to the wide range of varied applications of the synthetic material they produced.^[29] Versions of this symbol have been used in other trademarks, corporate logos, and emblems including those of Fujitsu,^[30] Cell Press,^[31] and the 2022 FIFA World Cup.^[32]

Encoding[edit]

The symbol is encoded in Unicode at U+221E ∞ INFINITY^[33] and in LaTeX as infty: .^[34] An encircled version is encoded for use as a symbol for acid-free paper.

Character information

Preview	∞	♾
Unicode name	INFINITY	PERMANENT PAPER SIGN
Encodings	decimal	hex	dec	hex
Unicode	8734	U+221E	9854	U+267E
UTF-8	226 136 158	E2 88 9E	226 153 190	E2 99 BE
GB 18030	161 222	A1 DE	129 55 174 56	81 37 AE 38
Numeric character reference	∞	∞	♾	♾
Named character reference	∞
OEM-437 (Alt Code)[35]	236	EC
Mac OS Roman[36]	176	B0
Symbol Font encoding[37]	165	A5
Shift JIS[38]	129 135	81 87
EUC-JP[39]	161 231	A1 E7
EUC-KR[40] / UHC[41]	161 196	A1 C4
EUC-KPS-9566[42]	162 172	A2 AC
Big5[43]	161 219	A1 DB
LaTeX[34]	infty	acidfree
CLDR text-to-speech name[44]	infinity sign	infinity

The Unicode set of symbols also includes several variant forms of the infinity symbol that are less frequently available in fonts in the block Miscellaneous Mathematical Symbols-B.^[45]

Character information

Preview	⧜	⧝	⧞
Unicode name	INCOMPLETE INFINITY	TIE OVER INFINITY	INFINITY NEGATED WITH VERTICAL BAR
Encodings	decimal	hex	dec	hex	dec	hex
Unicode	10716	U+29DC	10717	U+29DD	10718	U+29DE
UTF-8	226 167 156	E2 A7 9C	226 167 157	E2 A7 9D	226 167 158	E2 A7 9E
Numeric character reference	⧜	⧜	⧝	⧝	⧞	⧞
Named character reference	⧜	⧝	⧞
LaTeX[34]	iinfin	tieinfty	nvinfty

See also[edit]

• Aleph number
• History of mathematical notation
• Lazy Eight (disambiguation)

References[edit]

Infinity symbol
In Unicode	U+221E ∞ INFINITY (∞)
Different from
Different from	U+267E ♾ PERMANENT PAPER SIGN U+26AD ⚭ MARRIAGE SYMBOL

The infinity symbol () is a mathematical symbol representing the concept of infinity. This symbol is also called a lemniscate,^[1] after the lemniscate curves of a similar shape studied in algebraic geometry,^[2] or «lazy eight», in the terminology of livestock branding.^[3]

This symbol was first used mathematically by John Wallis in the 17th century, although it has a longer history of other uses. In mathematics, it often refers to infinite processes (potential infinity) rather than infinite values (actual infinity). It has other related technical meanings, such as the use of long-lasting paper in bookbinding, and has been used for its symbolic value of the infinite in modern mysticism and literature. It is a common element of graphic design, for instance in corporate logos as well as in older designs such as the Métis flag.

Both the infinity symbol itself and several variations of the symbol are available in various character encodings.

History[edit]

The lemniscate has been a common decorative motif since ancient times; for instance it is commonly seen on Viking Age combs.^[4]

The English mathematician John Wallis is credited with introducing the infinity symbol with its mathematical meaning in 1655, in his De sectionibus conicis.^[5][6][7] Wallis did not explain his choice of this symbol. It has been conjectured to be a variant form of a Roman numeral, but which Roman numeral is unclear. One theory proposes that the infinity symbol was based on the numeral for 100 million, which resembled the same symbol enclosed within a rectangular frame.^[8] Another proposes instead that it was based on the notation CIↃ used to represent 1,000.^[9] Instead of a Roman numeral, it may alternatively be derived from a variant of ω, the lower-case form of omega, the last letter in the Greek alphabet.^[9]

Perhaps in some cases because of typographic limitations, other symbols resembling the infinity sign have been used for the same meaning.^[7] Leonhard Euler used an open letterform more closely resembling a reflected and sideways S than a lemniscate,^[10] and even «O–O» has been used as a stand-in for the infinity symbol itself.^[7]

Usage[edit]

Mathematics[edit]

In mathematics, the infinity symbol is used more often to represent a potential infinity,^[11] rather than an actually infinite quantity as included in the extended real numbers, the cardinal numbers and the ordinal numbers (which use other notations, such as and ω, for infinite values). For instance, in mathematical expressions with summations and limits such as

the infinity sign is conventionally interpreted as meaning that the variable grows arbitrarily large towards infinity, rather than actually taking an infinite value, although other interpretations are possible.^[12]

The infinity symbol may also be used to represent a point at infinity, especially when there is only one such point under consideration. This usage includes, in particular, the infinite point of a projective line,^[13] and the point added to a topological space to form its one-point compactification.^[14]

Other technical uses[edit]

In areas other than mathematics, the infinity symbol may take on other related meanings. For instance, it has been used in bookbinding to indicate that a book is printed on acid-free paper and will therefore be long-lasting.^[15] On cameras and their lenses, the infinity symbol indicates that the lens’s focal length is set to an infinite distance, and is «probably one of the oldest symbols to be used on cameras».^[16]

Symbolism and literary uses[edit]

In modern mysticism, the infinity symbol has become identified with a variation of the ouroboros, an ancient image of a snake eating its own tail that has also come to symbolize the infinite, and the ouroboros is sometimes drawn in figure-eight form to reflect this identification—rather than in its more traditional circular form.^[18]

In the works of Vladimir Nabokov, including The Gift and Pale Fire, the figure-eight shape is used symbolically to refer to the Möbius strip and the infinite, as is the case in these books’ descriptions of the shapes of bicycle tire tracks and of the outlines of half-remembered people. Nabokov’s poem after which he entitled Pale Fire explicitly refers to «the miracle of the lemniscate».^[19] Other authors whose works use this shape with its symbolic meaning of the infinite include James Joyce, in Ulysses,^[20] and David Foster Wallace, in Infinite Jest.^[21]

Graphic design[edit]

The well-known shape and meaning of the infinity symbol have made it a common typographic element of graphic design. For instance, the Métis flag, used by the Canadian Métis people since the early 19th century, is based around this symbol.^[22] Different theories have been put forward for the meaning of the symbol on this flag, including the hope for an infinite future for Métis culture and its mix of European and First Nations traditions,^[23][24] but also evoking the geometric shapes of Métic dances,^[25], Celtic knots,^[26] or Plains First Nations Sign Language.^[27]

A rainbow-coloured infinity symbol is also used by the neurodiversity movement, as a way to symbolize the infinite variation of the people in the movement and of human cognition.^[28] The Bakelite company took up this symbol in its corporate logo to refer to the wide range of varied applications of the synthetic material they produced.^[29] Versions of this symbol have been used in other trademarks, corporate logos, and emblems including those of Fujitsu,^[30] Cell Press,^[31] and the 2022 FIFA World Cup.^[32]

Encoding[edit]

The symbol is encoded in Unicode at U+221E ∞ INFINITY^[33] and in LaTeX as infty: .^[34] An encircled version is encoded for use as a symbol for acid-free paper.

Character information

Preview	∞	♾
Unicode name	INFINITY	PERMANENT PAPER SIGN
Encodings	decimal	hex	dec	hex
Unicode	8734	U+221E	9854	U+267E
UTF-8	226 136 158	E2 88 9E	226 153 190	E2 99 BE
GB 18030	161 222	A1 DE	129 55 174 56	81 37 AE 38
Numeric character reference	∞	∞	♾	♾
Named character reference	∞
OEM-437 (Alt Code)[35]	236	EC
Mac OS Roman[36]	176	B0
Symbol Font encoding[37]	165	A5
Shift JIS[38]	129 135	81 87
EUC-JP[39]	161 231	A1 E7
EUC-KR[40] / UHC[41]	161 196	A1 C4
EUC-KPS-9566[42]	162 172	A2 AC
Big5[43]	161 219	A1 DB
LaTeX[34]	infty	acidfree
CLDR text-to-speech name[44]	infinity sign	infinity

The Unicode set of symbols also includes several variant forms of the infinity symbol that are less frequently available in fonts in the block Miscellaneous Mathematical Symbols-B.^[45]

Character information

Preview	⧜	⧝	⧞
Unicode name	INCOMPLETE INFINITY	TIE OVER INFINITY	INFINITY NEGATED WITH VERTICAL BAR
Encodings	decimal	hex	dec	hex	dec	hex
Unicode	10716	U+29DC	10717	U+29DD	10718	U+29DE
UTF-8	226 167 156	E2 A7 9C	226 167 157	E2 A7 9D	226 167 158	E2 A7 9E
Numeric character reference	⧜	⧜	⧝	⧝	⧞	⧞
Named character reference	⧜	⧝	⧞
LaTeX[34]	iinfin	tieinfty	nvinfty

See also[edit]

• Aleph number
• History of mathematical notation
• Lazy Eight (disambiguation)

References[edit]

Знак бесконечности (∞) — это символ, который используется для определения чего-то безграничного/бесконечного. Его используют в математике, физике, философии и других науках.

Кодировка символа бесконечности

Платформа	Сочетание клавиш	Описание
Компьютер с Windows	Alt + 236	удерживая клавишу ALT, набрать 236 на цифровой клавиатуре;
Apple macOS	Option + 5	удерживая клавишу Option, нажать 5;
Microsoft word и Microsoft excel	Вставка → Символ → Другие символы → Код знака:221E Скопировать ∞ Ctrl+C → Ctrl+V Alt + 236	слева будет «Вставка», в правом верхнем углу будет «Символ» скопировать знак здесь ∞ и вставить в документ удерживая клавишу ALT, набрать 236 на цифровой клавиатуре;
Вебсайт	Ctrl+C → Ctrl+V	Скопировать знак здесь ∞ и вставить его на свою веб-страницу
Код для ВК	‎&‎#9854 ♾
Facebook, инстаграм и т. д.	Ctrl+C → Ctrl+V	Скопировать знак здесь ∞
Символ бесконечности HTML	&‎#8734
Юникод	U+221E
CSS-код	221E
ASCII	236
LaTeX и MATLAB	infty

Значение знака бесконечности

Символ бесконечности обозначает идею безграничности или вечности. Зачастую используется в математике и метафорически относительно любви.

В математике этот символ используется как число, но бесконечность не является чем-то конкретным, это лишь концепция.

Если говорить о любви, то эти два взаимосвязанных круга, каждый из которых представляет собой человека в отношениях, изображают идею «быть навсегда вместе».

Символ бесконечности также может выражать чувство простоты и равновесия. Он напоминает, что наши возможности бесконечны.

Символ бесконечности используется и в медитации, чтобы напомнить человеку о ценности равновесия, сосредоточенности, единства, гармонии и мира.

История знака бесконечности

Символ бесконечности (∞) был создан Джоном Уоллисом, английским математиком в 1655 году. Однако само понятие бесконечности было задокументировано ещё с древнегреческих времён.

Учение «апейрон» философа Анаксимандра

Самые ранние записи идеи бесконечности датируются ещё 610 – 546 гг.

Древнегреческий философ Анаксимандр полагал, что Вселенная возникла из апейрона (вечное движение времени), на греческом это означает «бесконечный» или «неограниченный».

Философия Анаксимандра заключалась в том, что апейрон приводит к тому, что по мере возникновения мира противоположности (такие как жар и холод, ночь и день) отделяются друг от друга.

Изображение змеи/дракона Уроборос

Посредством изображения Уроборос (змеи, которая поедала свой собственный хвост) мир искусства передал идею, похожую на бесконечность. Этот образ считается самым старым и известным изображением бесконечности. Уроборос был у греков в 400 году нашей эры, но символ фактически восходит ещё к Древнему Египту, к 14 веку до нашей эры.

Иногда Уроборос изображается как две переплетённые змеи, или как змея в форме восьмёрки, или в форме круга. Зачастую это изображение интерпретируется как цикл жизни и смерти, но существуют и другие толкования.

Использование знака бесконечности

Символ бесконечности используется в своём первоначальном значении в таких областях, как: математика, физика, информатика. Его часто применяют и в графическом дизайне, чтобы подать мысль о постоянстве, стабильности и вечности. Его часто используют в логотипах.

Влюблённая пара может использовать предметы бижутерии (или даже сделать татуировки) с этим знаком, чтобы показать свою вечную любовь друг к другу.

Однако этот символ можно увидеть настолько часто (особенно татуировки), что в последнее время его стали больше использовать с юмором, иронией или даже сарказмом.

Смотрите также значение Иронии.

Символ бесконечности
∞
Изображение
◄ (b) √ (b) ∛ (b) ∜ (b) ∝ (b) ∞ ∟ (b) ∠ (b) ∡ (b) ∢ (b) ► (b)
Характеристики
Название	infinity
Юникод	U+221E
HTML-код	∞ или ∞
UTF-16	0x221E
URL-код	%E2%88%9E
Мнемоника	∞

Символ бесконечности(∞) — математический символ (b) , представляющий концепцию бесконечности (b) .

История

Введение символа бесконечности в математическом смысле в его современном виде принадлежит английскому математику Валлису (b) , который впервые использовал этот символ в своём трактате 1655 года «О конических сечениях (b) » (лат. (b)  De sectionibus conicis)^[1][2][3][4]. В своей книге Валлис никак не объяснил выбор этого символа для обозначения бесконечности, по некоторым предположениям, это мог быть вариант записи числа 1000 (b) римскими цифрами (b) (первоначально выглядевшей как CIƆ, либо CƆ), или буквы омега (b) (ω) — последней буквы греческого алфавита^[5].

Леонард Эйлер (b) использовал особый, открытый вариант символа бесконечности^[6] для того, чтобы обозначить «абсолютную бесконечность» (лат. (b)  absolutus infinitus). Этот символ бесконечности впоследствии никем не использовался и не представлен в Юникоде (b) .

Использование

В математике символ бесконечности используется чаще всего для выражения потенциальной бесконечности (b) ^[2], а не обозначения каких-то реальных бесконечно больших величин. Например, в математическом обозначении предела (b) :

,

знак бесконечности можно условно интерпретировать в том смысле, что переменная (b) достигает сколь угодно больших значений (стремится к бесконечности), но не принимает значения, равного бесконечности.

В топологии (b) символом бесконечности обозначается дополнительная точка, которая вводится при одноточечной компактификации (b) Александрова. Аналогично, в комплексном анализе (b) и проективной геометрии (b) символ обозначает бесконечно удалённую точку.

Но в областях математики, в которых возникает необходимость сравнивать и различать между различными типами бесконечности, для конкретных бесконечных величин вместо символа используются иные обозначения. Например, в теории множеств (b) , бесконечное кардинальное число множества (b) натуральных чисел (b) (мощность множества всех натуральных чисел) обозначается символом (читается «алеф (b) -нуль»), бесконечное кардинальное число множества счётных (b) порядковых чисел (b) обозначается , при этом . См. Иерархия алефов (b) .

В других отраслях символ бесконечности может иметь другой смысл; например, в переплётном (b) деле он используется для указания, что книга напечатана на долговечной бумаге^[7].

Символика

В современной мистике (b) символ бесконечности нередко отождествляется с образом Уробороса (b)  — змеи, поедающей собственный хвост^[8].

Владимир Набоков (b) в таких своих произведениях, как «Дар (b) » и «Бледный огонь (b) », использует символический образ восьмёрки (в частности, в виде ленты Мёбиуса (b) и символа бесконечности) в описаниях форм велосипедных шин и очертаний полузабытых людей. В поэме «Бледный огонь» упоминается, например «чудо лемнискаты (b) »^[9].

Применение в графическом дизайне

Символ бесконечности в настоящее время стал популярным элементом графического дизайна (b) . Например, это изображение является основным на флаге канадских метисов (b) , под которым сторонники Северо-западной компании (b) выступили в сражении у семи дубов  (англ.) (рус. (b) 1816 года^[10].

Многие современные крупные компании используют символ бесконечности в своих корпоративных логотипах (b) , в частности, Infiniti (b) , Room for PlayStation Portable (b) ^[en], Microsoft Visual Studio (b) , CoorsTek (b) ^[en], Meta (b) и другие.

Версии этого символа использовались в других товарных знаках, корпоративных логотипах и эмблемах, включая Fujitsu (b) ^[11] , Cell Press (b) ^[12],  и Чемпионат мира по футболу 2022 года (b) ^[13] .

Кодировка

В Юникоде (b) бесконечность обозначена символом ∞ (U+221E), в макропакете LaTeX (b) как (infty), имеются также другие варианты кодировки^[14].

См. также

• История математических обозначений (b)

Примечания

1. ↑ De sectionibus conicis nova methodo expositis tractatus — John Wallis — Google Boeken. Books.google.com. Дата обращения: 1 декабря 2013. Архивировано 2 января 2014 года.
2. 1 2 Barrow, John D. (b) (2008), Infinity: Where God Divides by Zero, Cosmic Imagery: Key Images in the History of Science, W. W. Norton & Company, с. 339–340, ISBN 9780393061772, <https://books.google.com/books?id=uRg6iN10JCIC&pg=PA339>Архивная копия от 18 августа 2020 на Wayback Machine (b)
3. ↑ Scott, Joseph Frederick (1981), The mathematical work of John Wallis, D.D., F.R.S., (1616-1703) (2 ed.), American Mathematical Society (b) , с. 24, ISBN 0-8284-0314-7, <https://books.google.com/books?id=XX9PKytw8g8C&pg=PA24>Архивная копия от 18 ноября 2016 на Wayback Machine (b)
4. ↑ Martin-Löf, Per (b) (1990), Mathematics of infinity, COLOG-88 (Tallinn, 1988), vol. 417, Lecture Notes in Computer Science (b) , Berlin: Springer, с. 146–197, DOI 10.1007/3-540-52335-9_54
5. ↑ Clegg, Brian (2003), A brief history of infinity: the quest to think the unthinkable, Robinson, ISBN 9781841196503
6. ↑ See for instance Cor. 1 p. 174 in: Leonhard Euler. Variae observationes circa series infinitas. Commentarii academiae scientiarum Petropolitanae 9, 1744, pp. 160—188. Архивная копия от 5 октября 2013 на Wayback Machine (b)
7. ↑ Zboray, Ronald J. & Zboray, Mary Saracino (2000), A handbook for the study of book history in the United States, Center for the Book, Library of Congress, с. 49, ISBN 9780844410159
8. ↑ O’Flaherty, Wendy Doniger (1986), Dreams, Illusion, and Other Realities, University of Chicago Press, с. 243, ISBN 9780226618555, <https://books.google.com/books?id=vhNNrX3bmo4C&pg=PA243>Архивная копия от 18 ноября 2016 на Wayback Machine (b) . The book also features this image on its cover.
9. ↑ Toker, Leona (1989), Nabokov: The Mystery of Literary Structures, Cornell University Press, с. 159, ISBN 9780801422119, <https://books.google.com/books?id=Jud1q_NrqpcC&pg=PA159>Архивная копия от 18 ноября 2016 на Wayback Machine (b)
10. ↑ Healy, Donald T. & Orenski, Peter J. (2003), Native American Flags, University of Oklahoma Press, с. 284, ISBN 978-0-8061-3556-4
11. ↑ Steve Rivkin, Fraser Sutherland. The Making of a Name: The Inside Story of the Brands We Buy. — Oxford University Press, 2005-01-13. — 286 с. — ISBN 978-0-19-988340-0.
12. ↑ Claudia Gisela Willmes. Science that Inspires (англ.) // Trends in Molecular Medicine. — 2021-01-01. — Т. 27, вып. 1. — С. 1. — ISSN (b) 1471-499X 1471-4914, 1471-499X. — doi (b) :10.1016/j.molmed.2020.11.001.
13. ↑ Qatar 2022: Football World Cup logo unveiled (англ.). www.aljazeera.com. Дата обращения: 16 октября 2022.
14. ↑ Unicode chart (odf) (PDF). Дата обращения: 1 декабря 2013. Архивировано 27 декабря 2017 года.

Ссылки

• ∞ на сайте Scriptsource.org (англ.)

Математические знаки (b)
Плюс (b) (+) Минус (b) (−) Знак умножения (b) (· или ×) Знак деления (b) (: или /) Обелюс (b) (÷) Знак корня (b) (√) Факториал (b) (!) Знак интеграла (b) (∫) Набла (b) (∇) Знак равенства (b) (=, ≈, ≡ и др.) Знаки неравенства (b) (≠, >, < и др.) Пропорциональность (b) (∝) Скобки (b) (( ), [ ], ⌈ ⌉, ⌊ ⌋, { }, ⟨ ⟩) Вертикальная черта (b) (|) Косая черта, слеш (b) (/) Обратная косая черта, бэкслеш (b) () Знак бесконечности (b) (∞) Знак градуса (b) (°) Штрих (b) (′, ″, ‴, ⁗) Звёздочка (b) (*) Процент (b) (%) Промилле (b) (‰) Тильда (b) (~) Карет (b) (^) Циркумфлекс (b) (ˆ) Плюс-минус (b) (±) Знак минус-плюс (∓) Десятичный разделитель (b) (, или .) Символ конца доказательства (b) (∎)
Таблица математических символов (b) История математических обозначений (b)

Символ бесконечности

Символ бесконечности — это математический символ, представляющий бесконечно большое число.

Символ бесконечности написан символом лемнискаты:

∞

Он представляет собой бесконечно положительное большое число.

Когда мы хотим написать бесконечно отрицательное число, мы должны написать:

-∞

Когда мы хотим написать бесконечно малое число, мы должны написать:

1 / ∞

Бесконечность — реальное число?

Бесконечность — это не число. Это не конкретное число, а бесконечно большое количество.

Правила и свойства бесконечности

название	Тип ключа
Положительная бесконечность	∞
Отрицательная бесконечность	-∞
Бесконечная разница	∞ — ∞ не определено
Нулевой продукт	0 ⋅ ∞ не определено
Коэффициент бесконечности	∞ / ∞ не определено
Сумма действительного числа	x + ∞ = ∞, для x ∈ℝ
Продукт с положительным числом	x ⋅ ∞ = ∞, для x / 0

Как набрать символ бесконечности на клавиатуре

Платформа	Тип ключа	Описание
Окна ПК	Alt + 2 3 6	Удерживая клавишу ALT, введите 236 на цифровой клавиатуре.
Macintosh	Вариант + 5	Удерживая клавишу Option, нажмите 5.
Microsoft Word	Я nsert/ S ymbol/ ∞	Выбор меню: I nsert/ S ymbol/ ∞
Alt + 2 3 6	Удерживая клавишу ALT, введите 236 на цифровой клавиатуре.
Майкрософт Эксель	Я nsert/ S ymbol/ ∞	Выбор меню: I nsert/ S ymbol/ ∞
Alt + 2 3 6	Удерживая клавишу ALT, введите 236 на цифровой клавиатуре.
страница интернета	Ctrl + C , Ctrl + V	Скопируйте отсюда ∞ и вставьте на свою веб-страницу.
Facebook	Ctrl + C , Ctrl + V	Скопируйте ∞ отсюда и вставьте на свою страницу в Facebook.
HTML	& infin; или & # 8734;
Код ASCII	236
Unicode	U + 221E
Латекс	infty
MATLAB	infty	Пример: title (‘График до infty’)

Бесконечность в теории множеств

Aleph-null ( ) — это бесконечное количество элементов (мощность) набора натуральных чисел ( ).

Алеф-единица ( ) — это бесконечное число элементов (мощность) счетного множества порядковых чисел (ω ₁ ).

Символы алгебры ►

---

Смотрите также

• Математические символы
• Символы исчисления
• Символы алгебры
• Логарифм бесконечности
• Ln бесконечности
• Арктан бесконечности
• Арксин бесконечности
• Символ бесконечности ALT-код
• Символ бесконечности на Mac
• Тип символа бесконечности на клавиатуре
• Тип бесконечности sumbol на Facebook
• Символ бесконечности в Word
• Бесконечность — реальное число

∞
Символ бесконечности
ВUnicode	U + 221E ∞ БЕСКОНЕЧНОСТЬ (HTML∞ · & infin;)
Отличный от
Отличный от	U + 267E ♾ ПОСТОЯННЫЙ БУМАЖНЫЙ ЗНАК (HTML♾)

В символ бесконечности (, ∞, или в юникод ∞) является математический символ представляя концепцию бесконечность. В алгебраическая геометрия, фигура называется лемниската.

История

Форма боковой восьмерки имеет длинную родословную; например, он появляется в кресте Святой Бонифаций, обернутые вокруг стержней Латинский крест.^[1] Однако, Джон Уоллис приписывают введение символа бесконечности с его математическим значением в 1655 году в его De sectionibus conicis.^{[1][2][3][4][5]} Уоллис не объяснил свой выбор этого символа, но было высказано предположение, что это вариант формы символа Римская цифра за 1000 (первоначально CIƆ, также CƆ,^[6] что иногда использовалось для обозначения «многие») или вариант греческой буквы ω (омега ) — последняя буква в Греческий алфавит.^[7]

Леонард Эйлер использовали открытый вариант символа^[8] для обозначения «absolutus infinitus». Эйлер свободно выполнял различные операции над бесконечность, например, взяв его логарифм. Этот символ больше не используется и не кодируется как отдельный символ в Unicode.

Применение

В математике символ бесконечности чаще используется для обозначения потенциальная бесконечность,^[1] а не фактически бесконечное количество, включенное в расширенные действительные числа, то порядковые номера и Количественные числительные (которые используют другие обозначения).^[9] Например, в математических выражениях с подведения итогов и пределы например, ниже:

знак бесконечности условно интерпретируется как означающий рост переменной произвольно большой к бесконечности — вместо того, чтобы принимать бесконечное значение.

Символ бесконечности также может использоваться для обозначения точка в бесконечности, особенно когда рассматривается только один такой момент. Это использование включает, в частности, бесконечную точку проективная линия,^[10][11] и точка добавлена ​​к топологическое пространство сформировать свой одноточечная компактификация .^[12]

В областях, отличных от математики, символ бесконечности может иметь другие связанные значения. Например, он использовался в переплетное дело чтобы указать, что книга напечатана на бескислотная бумага и, следовательно, будет долговечным.^[13]

Современный символизм

В современном мистицизме символ бесконечности отождествляется с разновидностью уроборос, древнее изображение змеи, поедающей свой собственный хвост, которое также стало символом бесконечности, и уроборос иногда рисуют в форме восьмерки, чтобы отразить это отождествление, а не в более традиционной круглой форме.^[14]

В произведениях Владимир Набоков, в том числе Подарок и Бледный огонь, восьмерка символически используется для обозначения Лента Мебиуса и бесконечное, как в случае с описаниями в этих книгах форм следов велосипедных шин и очертаний полузабытых людей. Поэма, после которой Бледный огонь под названием прямо говорится о «чуде лемнискаты».^[15]

Графический дизайн

Хорошо известная форма и значение символа бесконечности сделали его обычным типографский элемент графический дизайн. Например, Метис флаг, используется канадской Метисы с начала 19 века основан на этом символе.^[16] А радуга -цветный символ бесконечности также используется движение за нейроразнообразие.^[17] В современной торговле корпоративные логотипы с этим символом использовались, среди прочего, Чемпионат мира по футболу 2022 года.^[18]

Кодирование

Символ закодирован в Unicode в U + 221E ∞ БЕСКОНЕЧНОСТЬ (HTML∞ · & infin;) ^[19]И в Латекс так как infty: .^[20]

Набор символов Unicode также включает несколько вариантов формы символа бесконечности, которые реже доступны в шрифтах: U + 29DC ⧜ НЕПОЛНАЯ БЕСКОНЕЧНОСТЬ (HTML⧜ · & iinfin; · Организация ISOtech ⧜), U + 29DD ⧝ НАВЯЗАТЬ НА БЕСКОНЕЧНОСТЬ (HTML⧝ · & infintie;) и U + 29DE ⧞ БЕСКОНЕЧНОСТЬ С ВЕРТИКАЛЬНОЙ ПОЛОСКОЙ (HTML⧞ · & nvinfin;) в блоке Разные математические символы-B.^[21]

Смотрите также

• История математической записи

использованная литература

Как написать знак бесконечность

Повернутая на 90° восьмерка впервые была использована для обозначения бесконечности английским математиком Джоном Уоллесом в трактате, опубликованном в 1655 году. Такого знака вы не найдете на клавиатуре, но в кодовых таблицах символов, используемых компьютером, он предусмотрен. Поэтому существуют и способы для вставки этого знака в большинство текстовых и гипертекстовых документов.

Инструкция

Не пытайтесь вставить знак бесконечности в текстовые документы, которые хранятся в файлах с расширением txt. Увы, формат таких документов рассчитан на работу только с первыми 128 символами кодовых таблиц, используемых компьютером, а символ бесконечности размещен гораздо дальше.

Используйте код 8734 для вставки этого символа в текстовые документы, которые могут отображать символы, включенные в юникод-таблицы. Установите курсор ввода в ту позицию в тексте, где должен быть знак бесконечности, и нажмите клавишу Alt. Удерживая эту клавишу, наберите на цифровой (дополнительной) клавиатуре код, а затем отпустите Alt, и знак бесконечности появится в тексте.

В текстовом процессоре Microsoft Office Word кроме приведенного в предыдущем шаге десятичного кода символа бесконечности можно использовать и его шестнадцатеричный эквивалент 221E (E — английская литера). Наберите его в нужном месте текста, а затем нажмите сочетание клавиш Alt и X — текстовый процессор заменит эти четыре символа одним знаком бесконечности.

Держать в памяти десятичные или шестнадцатеричные коды не очень удобно, поэтому в приложении Microsoft Word лучше пользоваться помещенным во вкладке «Вставка» выпадающим списком символов — ищите его в крайней справа группе команд. В этот список попадают двадцать последних символов из недавно использовавшихся, поэтому первый раз вам придется воспользоваться полной версией таблицы символов. Откройте ее, выбрав в выпадающем списке строку «Другие символы». В поле «Набор» установите значение «математические операторы», кликните символ бесконечности в таблице символов и нажмите кнопку «Вставить».

В гипертекстовых документах с юникод-кодировкой используйте для отображения нестандартных знаков символьные примитивы языка HTML 4. Для вывода на страницу знака бесконечности в ее исходный код надо поместить набор символов &infin;. Можно воспользоваться и шестнадцатеричным кодом этого знака — набор символов ∞ отобразит на гипертекстовой странице такой же знак бесконечности.

Видео по теме

Источники:

• как пишется знак меньше в математике
• По настоящему интересное значение татуировки бесконечность

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Содержание

• Использование кода для вставки знака бесконечности
  • Цифровой код
  • Шестнадцатеричный код
• Вопросы и ответы

Активные пользователи Microsoft Word хорошо знают о наборе символов и специальных знаков, содержащихся в арсенале этой замечательной программы. Все они находятся в окне «Символ», расположенном во вкладке «Вставка». В этом разделе представлен действительно огромный набор символов и знаков, удобно рассортированных по группам и темам.

Урок: Вставка символов в Ворде

Каждый раз, когда возникает необходимость поставить какой-либо знак или символ, отсутствующий на клавиатуре, знайте, искать его нужно именно в меню «Символ». Точнее, в подменю этого раздела, получившем название «Другие символы».

Урок: Как вставить знак дельты в Word

Огромный выбор знаков — это, конечно, хорошо, вот только в этом обилии иногда очень сложно найти то, что нужно. Один из таких символов — это знак бесконечности, о вставке которого в документе Ворд мы и расскажем.

Использование кода для вставки знака бесконечности

Хорошо, что разработчики Microsoft Word не только интегрировали в свое офисное детище множество знаков и символов, но и наделили каждый из них специальным кодом. Более того, зачастую этих кодов даже два. Зная хотя бы один из них, а также комбинацию клавиш, которая преобразует этот самый код в вожделенный символ, можно работать в Ворде куда быстрее.

Цифровой код

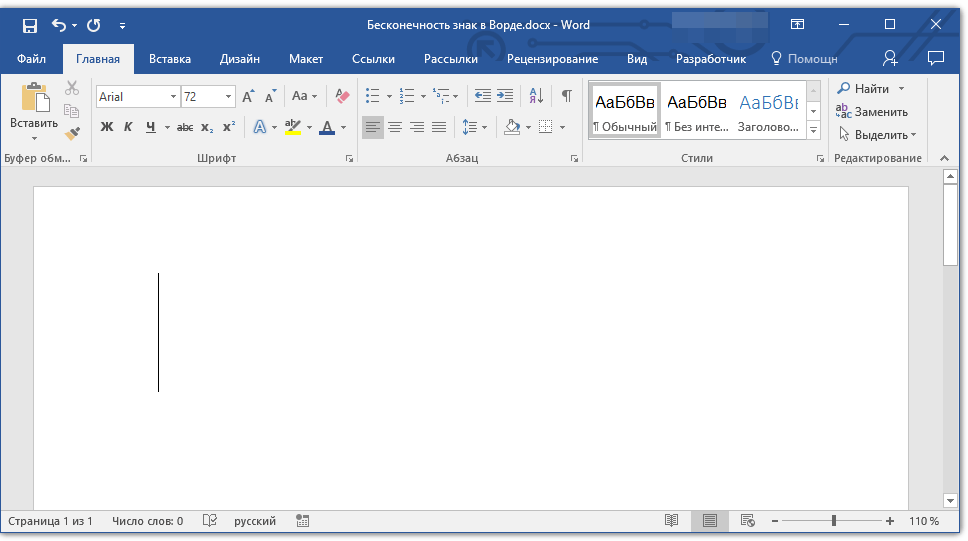
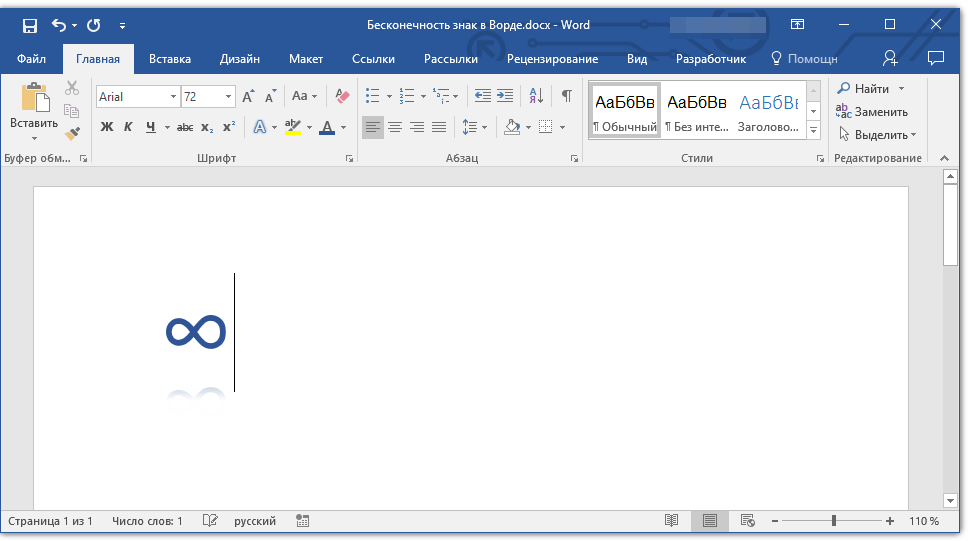
1. Установите курсор в месте, где должен находиться знак бесконечности, и зажмите клавишу «ALT».

2. Не отпуская клавишу, на цифровой клавиатуре наберите цифры «8734» без кавычек.

3. Отпустите клавишу «ALT», в указанном месте появится знак бесконечности.

Урок: Вставка знака телефона в Word

Шестнадцатеричный код

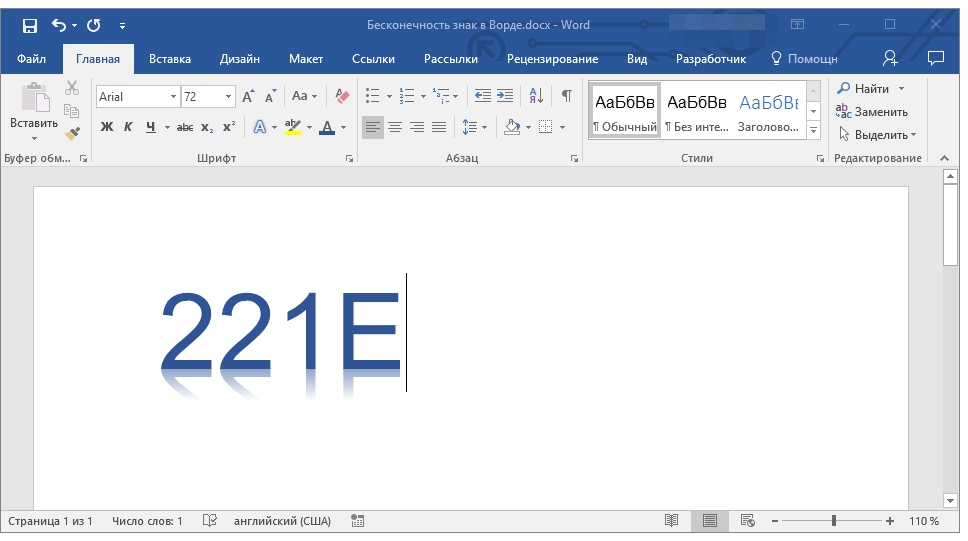
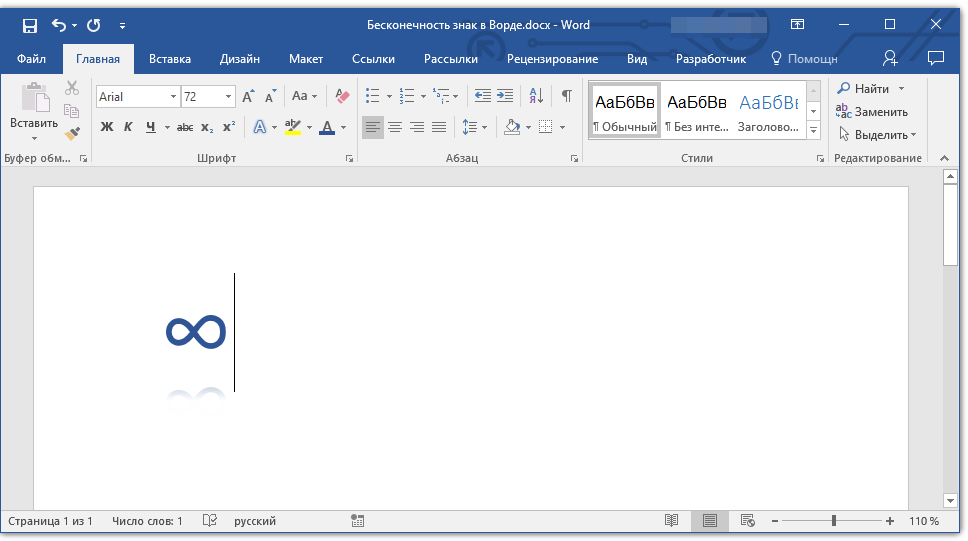
1. В месте, где должен находиться знак бесконечности, введите в английской раскладке код «221E» без кавычек.

2. Нажмите клавиши «ALT+X», чтобы преобразовать введенный код в знак бесконечности.

Урок: Вставка знака «крестик в квадратике» в Ворде

Вот так просто можно поставить знак бесконечности в Microsoft Word. Какой из вышеописанных методов выбрать, решать вам, главное, чтобы это было удобно и оперативно.

Мы рады, что смогли помочь Вам в решении проблемы.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

Еще статьи по данной теме: