Как пишется знак пересекает

Морфемный разбор слова:

Однокоренные слова к слову:

Знак пересечения

Определение

Знак пересечения – это символ, указывающий на пересечение прямых, углов, лучей, отрезков, плоскостей и других фигур в геометрии, пересечение множеств в математике (алгебре) и информатике.

Как пишется этот символ пересечения?

Этот знак выглядит и пишется так – ⋂

Его достаточно легко запомнить, он похож на русскую букву «П», начальную букву слова «пересечение».

Как быстро запомнить этот знак?

Просто представьте себе и запомните, что этот символ выглядит как буква «П» и похож на подкову, перевернутую вниз ногами.

Как применяется знак ⋂?

Применяется для обозначения пересечения прямых, углов, лучей, отрезков в геометрии, пересечение множеств в математике (алгебре) и информатике.

Как выглядит знак «не пересечения» в геометрии?

Пример

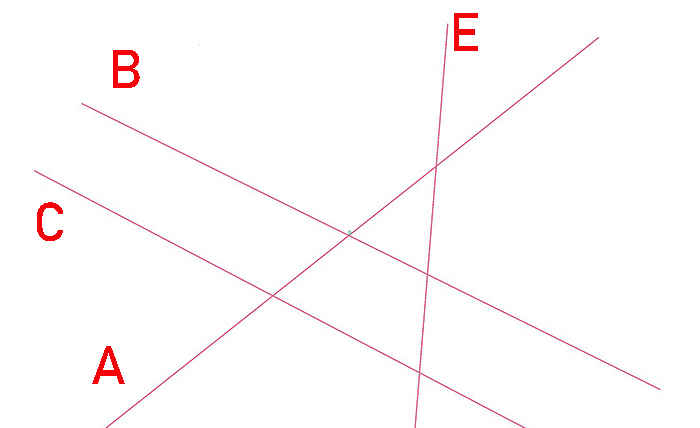
А ∩ С = ∅ — 2 луча или (2 прямые, 2отрезка) А и С не пересекаются.

Что обозначает знак пересечения наоборот?

Это символ выглядит и пишется следующим образом: ∪

Обозначается термином – «объединение».

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Обозначения и символика

Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).

Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:

группа I — обозначения геометрических фигур и отношений между ними;

группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.

Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.

СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ

А. Обозначение геометрических фигур

1. Геометрическая фигура обозначается — Ф.

2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:

3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:

Линии уровня обозначаются: h — горизонталь; f— фронталь.

Для прямых используются также следующие обозначения:

(АВ) — прямая, проходящая через точки А а В;

[АВ) — луч с началом в точке А;

[АВ] — отрезок прямой, ограниченный точками А и В.

4. Поверхности обозначаются строчными буквами греческого алфавита:

Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:

α(а || b) — плоскость α определяется параллельными прямыми а и b;

5. Углы обозначаются:

6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:

— величина угла АВС;

— величина угла φ.

Прямой угол отмечается квадратом с точкой внутри

7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.

|АВ| — расстояние между точками А и В (длина отрезка АВ);

|Аа| — расстояние от точки А до линии a;

|Аα| — расстояшие от точки А до поверхности α;

|аb| — расстояние между линиями а и b;

|αβ| расстояние между поверхностями α и β.

π₂ —фрюнтальная плоскость проекций.

При замене плоскостей проекций или введении новых плоскостей последние обозначают π₃, π₄ и т. д.

Постояшную прямую эпюра Монжа обозначают k.

10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:

11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса _0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.

12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.

Например: H_a — горизонтальный след прямой (линии) а;

F_a — фронтальный след прямой (линии ) a.

13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами _{1,2,3. n:}

Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом ₀:

14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0 :

15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :

Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.

Источник

Лучший ответ

Максим Ковалев

Профи

(920)


13 лет назад

пересечение обозначается так ∩ я нашел его в символах

Витя ГрабоварУченик (202)

5 лет назад

спасибо! Ты очень помог!

Остальные ответы

Юлия Хуторная

Просветленный

(36782)


13 лет назад

этот значок похож на арку

A-Gem

Знаток

(333)


13 лет назад

на клаве к сжалению такоко значка нет, но попробую объяснить: переверни U наоборот, мы этот знак «радугой» называем=)))

Ирина ВербицкаяЗнаток (496)

1 год назад

Ну и как «радугу» поставить над буквами в документе? Надо переписать старый учебник и у меня не получается поставить этот значок.

Умка

Ученик

(103)


13 лет назад

подкова, только кверх ногами!

Gala

Мыслитель

(5452)


13 лет назад

U-это знак объединения, переверни-получится знак пересечения

Гоар Бернецян

Ученик

(137)


6 лет назад

спасибо, выручили

Мери теккозян

Ученик

(136)


6 лет назад

Этот знак используется не только в геометрии и изображается ∩

Vladis )

Знаток

(425)


5 лет назад

∩

Хо Минхо

Профи

(690)


5 лет назад

∩ — знак пересечения

Александра Соболева

Ученик

(119)


5 лет назад

радуга

Lev Matveev

Ученик

(242)


5 лет назад

∩ радуга, арка, подкова верх ногами.

АСВысший разум (138139)

4 года назад

https://otvet.mail.ru/question/206345385 — подсказка: 3y² — 2x² — xy — 5y + 2 = 0, x² + y² = 1
3y² — 2x² — xy — 5y + 2 = (x-y+1)(2x+3y-2)=0
x-y+1=0 и 2x+3y-2=0 — уравнение прямых, x² + y² = 1 — уравнение окружности
Вот и решай системы:
x-y+1=0, x² + y² = 1 и x+3y-2=0, x² + y² = 1
В результате получишь ЧЕТЫРЕ пары решений

DYRAK

Профи

(538)


5 лет назад

∩ это пересечение U это обьеденение

Настя Пунюшкина

Ученик

(141)


4 года назад

U так только переверни

Александр Давыдов

Знаток

(377)


3 года назад

∩

Ҝρนĉ⍡นӈα

Гуру

(3130)


3 года назад

∩

hito_pae

Профи

(650)


8 месяцев назад

∩

0 интересует


0 не интересует

ответил

27 Март, 18


от
kravchenkoanyu_zn
Начинающий

(136 баллов)

Лучший ответ

Мне кажется так,просто я ещё не изучаю геометрию. 

---

Определение

Знак пересечения – это символ, указывающий на пересечение прямых, углов, лучей, отрезков, плоскостей и других фигур в геометрии, пересечение множеств в математике (алгебре) и информатике.

Как пишется этот символ пересечения?

Этот знак выглядит и пишется так – ⋂

Его достаточно легко запомнить, он похож на русскую букву «П», начальную букву слова «пересечение».

Как быстро запомнить этот знак?

Просто представьте себе и запомните, что этот символ выглядит как буква «П» и похож на подкову, перевернутую вниз ногами.

Как применяется знак ⋂?

Применяется для обозначения пересечения прямых, углов, лучей, отрезков в геометрии, пересечение множеств в математике (алгебре) и информатике.

Как выглядит знак «не пересечения» в геометрии?

Пример

А ∩ С = ∅ — 2 луча или (2 прямые, 2отрезка) А и С не пересекаются.

Что обозначает знак пересечения наоборот?

Это символ выглядит и пишется следующим образом: ∪

Обозначается термином – «объединение».

Опубликовано — 2 года назад | По предмету
Геометрия |
автор julia2000B

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

{} набор набор элементов A = {3,7,9,14},
B = {9,14,28} А ∩ Б пересечение объекты, принадлежащие множеству A и множеству B A ∩ B = {9,14} А ∪ Б союз объекты, принадлежащие множеству A или множеству B A ∪ B = {3,7,9,14,28} А ⊆ Б подмножество A является подмножеством B. множество A включено в набор B. {9,14,28} ⊆ {9,14,28} A ⊂ B правильное подмножество / строгое подмножество A является подмножеством B, но A не равно B. {9,14} ⊂ {9,14,28} А ⊄ Б не подмножество множество A не является подмножеством множества B {9,66} ⊄ {9,14,28} А ⊇ Б суперсет A является надмножеством B. множество A включает множество B {9,14,28} ⊇ {9,14,28} А ⊃ Б правильный суперсет / строгий суперсет A является надмножеством B, но B не равно A. {9,14,28} ⊃ {9,14} А ⊅ Б не суперсет множество A не является надмножеством множества B {9,14,28} ⊅ {9,66} 2 ^А набор мощности все подмножества A   набор мощности все подмножества A   А = В равенство оба набора имеют одинаковые элементы A = {3,9,14},
B = {3,9,14},
A = B А ^в дополнять все объекты, не принадлежащие множеству A   А Б относительное дополнение объекты, принадлежащие A, а не B A = {3,9,14},
B = {1,2,3},
AB = {9,14} А — Б относительное дополнение объекты, принадлежащие A, а не B A = {3,9,14},
B = {1,2,3},
AB = {9,14} A ∆ B симметричная разница объекты, принадлежащие A или B, но не их пересечение A = {3,9,14},
B = {1,2,3},
A ∆ B = {1,2,9,14} А ⊖ Б симметричная разница объекты, принадлежащие A или B, но не их пересечение A = {3,9,14},
B = {1,2,3},
A ⊖ B = {1,2,9,14} a ∈A элемент,
принадлежит установить членство A = {3,9,14}, 3 ∈ A x ∉A не элемент нет установленного членства A = {3,9,14}, 1 ∉ A ( а , б ) упорядоченная пара сборник из 2-х элементов   A × B декартово произведение множество всех упорядоченных пар из A и B   | A | мощность количество элементов множества A A = {3,9,14}, | A | = 3 #A мощность количество элементов множества A A = {3,9,14}, # A = 3 | вертикальная полоса такой, что А = {х | 3 <х <14} алеф-нуль бесконечная мощность множества натуральных чисел   алеф-он мощность множества счетных порядковых чисел   Ø пустой набор Ø = {} C = {Ø} универсальный набор набор всех возможных значений   ₀ набор натуральных / целых чисел (с нулем) ₀ = {0,1,2,3,4, …} 0 ∈ _{0 1} набор натуральных / целых чисел (без нуля) ₁ = {1,2,3,4,5, …} 6 ∈ ₁ набор целых чисел = {…- 3, -2, -1,0,1,2,3, …} -6 ∈ набор рациональных чисел = { x | x = a / b , a , b ∈ } 2/6 ∈ набор реальных чисел = { x | -∞ < х <∞} 6.343434∈ набор комплексных чисел = { z | z = a + bi , -∞ < a <∞, -∞ < b <∞} 6 + 2 i ∈