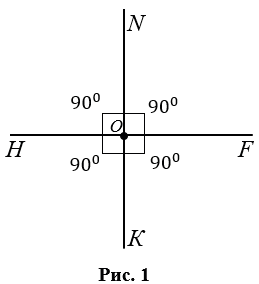⟂ Перпендикуляр
Нажмите, чтобы скопировать и вставить символ
Значение символа
Перпендикуляр. Разные математические символы — A.
Символ «Перпендикуляр» был утвержден как часть Юникода версии 4.1 в 2005 г.
Свойства
| Версия | 4.1 |
| Блок | Разные математические символы — A |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 27C2 |
| Простое изменение регистра | 27C2 |
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 9F 82 | 226 159 130 | 14851970 | 11100010 10011111 10000010 |
| UTF-16BE | 27 C2 | 39 194 | 10178 | 00100111 11000010 |
| UTF-16LE | C2 27 | 194 39 | 49703 | 11000010 00100111 |
| UTF-32BE | 00 00 27 C2 | 0 0 39 194 | 10178 | 00000000 00000000 00100111 11000010 |
| UTF-32LE | C2 27 00 00 | 194 39 0 0 | 3257335808 | 11000010 00100111 00000000 00000000 |
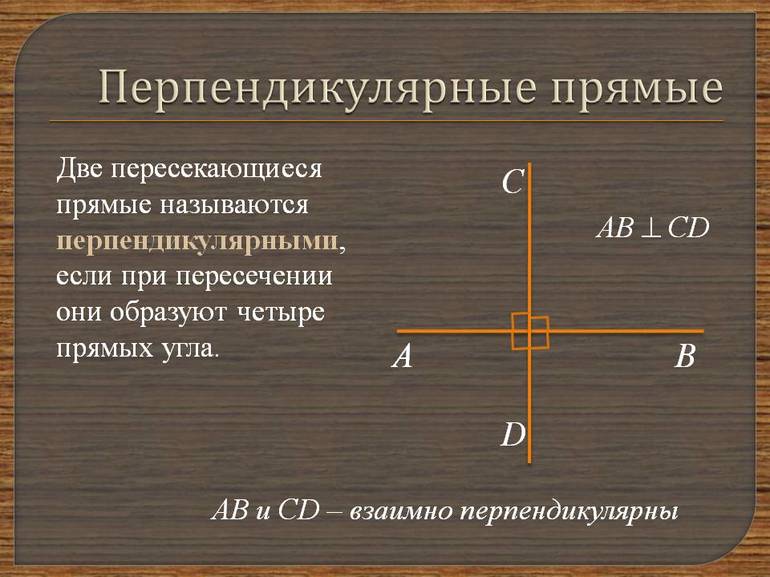
The segment AB is perpendicular to the segment CD because the two angles it creates (indicated in orange and blue) are each 90 degrees. The segment AB can be called the perpendicular from A to the segment CD, using «perpendicular» as a noun. The point B is called the foot of the perpendicular from A to segment CD, or simply, the foot of A on CD.[1]
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians). The condition of perpendicularity may be represented graphically using the perpendicular symbol, ⟂. It can be defined between two lines (or two line segments), between a line and a plane, and between two planes.
Perpendicularity is one particular instance of the more general mathematical concept of orthogonality; perpendicularity is the orthogonality of classical geometric objects. Thus, in advanced mathematics, the word «perpendicular» is sometimes used to describe much more complicated geometric orthogonality conditions, such as that between a surface and its normal vector.
Definitions[edit]
A line is said to be perpendicular to another line if the two lines intersect at a right angle.[2] Explicitly, a first line is perpendicular to a second line if (1) the two lines meet; and (2) at the point of intersection the straight angle on one side of the first line is cut by the second line into two congruent angles. Perpendicularity can be shown to be symmetric, meaning if a first line is perpendicular to a second line, then the second line is also perpendicular to the first. For this reason, we may speak of two lines as being perpendicular (to each other) without specifying an order.
Perpendicularity easily extends to segments and rays. For example, a line segment 


A line is said to be perpendicular to a plane if it is perpendicular to every line in the plane that it intersects. This definition depends on the definition of perpendicularity between lines.
Two planes in space are said to be perpendicular if the dihedral angle at which they meet is a right angle.
Foot of a perpendicular[edit]
The word foot is frequently used in connection with perpendiculars. This usage is exemplified in the top diagram, above, and its caption. The diagram can be in any orientation. The foot is not necessarily at the bottom.
More precisely, let A be a point and m a line. If B is the point of intersection of m and the unique line through A that is perpendicular to m, then B is called the foot of this perpendicular through A.
Construction of the perpendicular[edit]
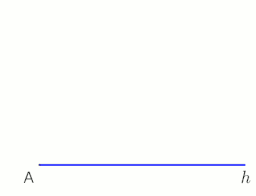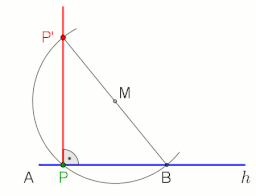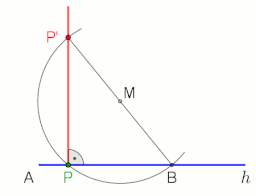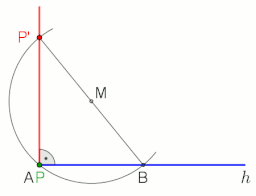
Construction of the perpendicular (blue) to the line AB through the point P.
Construction of the perpendicular to the half-line h from the point P (applicable not only at the end point A, M is freely selectable), animation at the end with pause 10 s
To make the perpendicular to the line AB through the point P using compass-and-straightedge construction, proceed as follows (see figure left):
- Step 1 (red): construct a circle with center at P to create points A’ and B’ on the line AB, which are equidistant from P.
- Step 2 (green): construct circles centered at A’ and B’ having equal radius. Let Q and P be the points of intersection of these two circles.
- Step 3 (blue): connect Q and P to construct the desired perpendicular PQ.
To prove that the PQ is perpendicular to AB, use the SSS congruence theorem for QPA’ and QPB’ to conclude that angles OPA’ and OPB’ are equal. Then use the SAS congruence theorem for triangles OPA’ and OPB’ to conclude that angles POA and POB are equal.
To make the perpendicular to the line g at or through the point P using Thales’s theorem, see the animation at right.
The Pythagorean theorem can be used as the basis of methods of constructing right angles. For example, by counting links, three pieces of chain can be made with lengths in the ratio 3:4:5. These can be laid out to form a triangle, which will have a right angle opposite its longest side. This method is useful for laying out gardens and fields, where the dimensions are large, and great accuracy is not needed. The chains can be used repeatedly whenever required.
In relationship to parallel lines[edit]
The arrowhead marks indicate that the lines a and b, cut by the transversal line c, are parallel.
If two lines (a and b) are both perpendicular to a third line (c), all of the angles formed along the third line are right angles. Therefore, in Euclidean geometry, any two lines that are both perpendicular to a third line are parallel to each other, because of the parallel postulate. Conversely, if one line is perpendicular to a second line, it is also perpendicular to any line parallel to that second line.
In the figure at the right, all of the orange-shaded angles are congruent to each other and all of the green-shaded angles are congruent to each other, because vertical angles are congruent and alternate interior angles formed by a transversal cutting parallel lines are congruent. Therefore, if lines a and b are parallel, any of the following conclusions leads to all of the others:
- One of the angles in the diagram is a right angle.
- One of the orange-shaded angles is congruent to one of the green-shaded angles.
- Line c is perpendicular to line a.
- Line c is perpendicular to line b.
In computing distances[edit]
In geometry, the perpendicular distance between two objects is the distance from one to the other, measured along a line that is perpendicular to one or both.
The distance from a point to a line is the distance to the nearest point on that line. That is the point at which a segment from it to the given point is perpendicular to the line.
Likewise, the distance from a point to a curve is measured by a line segment that is perpendicular to a tangent line to the curve at the nearest point on the curve.
The distance from a point to a plane is measured as the length from the point along a segment that is perpendicular to the plane, meaning that it is perpendicular to all lines in the plane that pass through the nearest point in the plane to the given point.
Other instances include:
- Point on plane closest to origin, for the perpendicular distance from the origin to a plane in three-dimensional space
- Nearest distance between skew lines, for the perpendicular distance between two non-parallel lines in three-dimensional space
Perpendicular regression fits a line to data points by minimizing the sum of squared perpendicular distances from the data points to the line.
Other geometric curve fitting methods using perpendicular distance to measure the quality of a fit exist, as in total least squares.
The concept of perpendicular distance may be generalized to
- orthogonal distance, between more abstract non-geometric orthogonal objects, as in linear algebra (e.g., principal components analysis);
- normal distance, involving a surface normal, between an arbitrary point and its foot on the surface. It can be used for surface fitting and for defining offset surfaces.
Graph of functions[edit]
In the two-dimensional plane, right angles can be formed by two intersected lines if the product of their slopes equals −1. Thus defining two linear functions: y1 = a1x + b1 and y2 = a2x + b2, the graphs of the functions will be perpendicular and will make four right angles where the lines intersect if a1a2 = −1. However, this method cannot be used if the slope is zero or undefined (the line is parallel to an axis).
For another method, let the two linear functions be: a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0. The lines will be perpendicular if and only if a1a2 + b1b2 = 0. This method is simplified from the dot product (or, more generally, the inner product) of vectors. In particular, two vectors are considered orthogonal if their inner product is zero.
In circles and other conics[edit]
Circles[edit]
Each diameter of a circle is perpendicular to the tangent line to that circle at the point where the diameter intersects the circle.
A line segment through a circle’s center bisecting a chord is perpendicular to the chord.
If the intersection of any two perpendicular chords divides one chord into lengths a and b and divides the other chord into lengths c and d, then a2 + b2 + c2 + d2 equals the square of the diameter.[4]
The sum of the squared lengths of any two perpendicular chords intersecting at a given point is the same as that of any other two perpendicular chords intersecting at the same point, and is given by 8r2 – 4p2 (where r is the circle’s radius and p is the distance from the center point to the point of intersection).[5]
Thales’ theorem states that two lines both through the same point on a circle but going through opposite endpoints of a diameter are perpendicular. This is equivalent to saying that any diameter of a circle subtends a right angle at any point on the circle, except the two endpoints of the diameter.
Ellipses[edit]
The major and minor axes of an ellipse are perpendicular to each other and to the tangent lines to the ellipse at the points where the axes intersect the ellipse.
The major axis of an ellipse is perpendicular to the directrix and to each latus rectum.
Parabolas[edit]
In a parabola, the axis of symmetry is perpendicular to each of the latus rectum, the directrix, and the tangent line at the point where the axis intersects the parabola.
From a point on the tangent line to a parabola’s vertex, the other tangent line to the parabola is perpendicular to the line from that point through the parabola’s focus.
The orthoptic property of a parabola is that If two tangents to the parabola are perpendicular to each other, then they intersect on the directrix. Conversely, two tangents which intersect on the directrix are perpendicular. This implies that, seen from any point on its directrix, any parabola subtends a right angle.
Hyperbolas[edit]
The transverse axis of a hyperbola is perpendicular to the conjugate axis and to each directrix.
The product of the perpendicular distances from a point P on a hyperbola or on its conjugate hyperbola to the asymptotes is a constant independent of the location of P.
A rectangular hyperbola has asymptotes that are perpendicular to each other. It has an eccentricity equal to 
In polygons[edit]
Triangles[edit]
The legs of a right triangle are perpendicular to each other.
The altitudes of a triangle are perpendicular to their respective bases. The perpendicular bisectors of the sides also play a prominent role in triangle geometry.
The Euler line of an isosceles triangle is perpendicular to the triangle’s base.
The Droz-Farny line theorem concerns a property of two perpendicular lines intersecting at a triangle’s orthocenter.
Harcourt’s theorem concerns the relationship of line segments through a vertex and perpendicular to any line tangent to the triangle’s incircle.
Quadrilaterals[edit]
In a square or other rectangle, all pairs of adjacent sides are perpendicular. A right trapezoid is a trapezoid that has two pairs of adjacent sides that are perpendicular.
Each of the four maltitudes of a quadrilateral is a perpendicular to a side through the midpoint of the opposite side.
An orthodiagonal quadrilateral is a quadrilateral whose diagonals are perpendicular. These include the square, the rhombus, and the kite. By Brahmagupta’s theorem, in an orthodiagonal quadrilateral that is also cyclic, a line through the midpoint of one side and through the intersection point of the diagonals is perpendicular to the opposite side.
By van Aubel’s theorem, if squares are constructed externally on the sides of a quadrilateral, the line segments connecting the centers of opposite squares are perpendicular and equal in length.
Lines in three dimensions[edit]
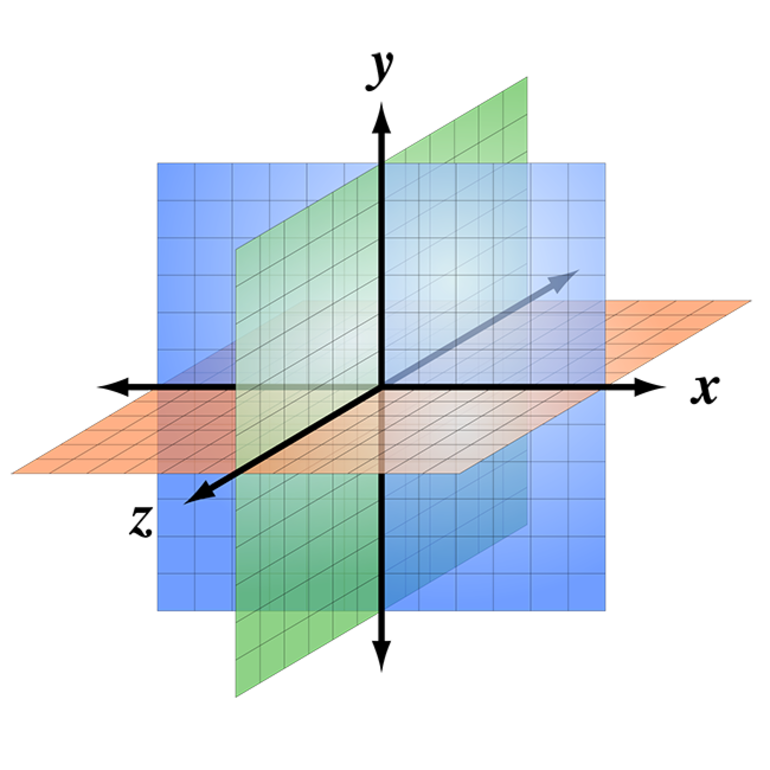
Up to three lines in three-dimensional space can be pairwise perpendicular, as exemplified by the x, y, and z axes of a three-dimensional Cartesian coordinate system.
See also[edit]
- Orthogonal projection
- Tangential and normal components
Notes[edit]
- ^ Kay (1969, p. 114)
- ^ Kay (1969, p. 91)
- ^ Kay (1969, p. 91)
- ^ Posamentier and Salkind, Challenging Problems in Geometry, Dover, 2nd edition, 1996: pp. 104–105, #4–23.
- ^ College Mathematics Journal 29(4), September 1998, p. 331, problem 635.
References[edit]
- Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble, LCCN 52-13504
- Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69-12075
External links[edit]
- Definition: perpendicular with interactive animation.
- How to draw a perpendicular bisector of a line with compass and straight edge (animated demonstration).
- How to draw a perpendicular at the endpoint of a ray with compass and straight edge (animated demonstration).
The segment AB is perpendicular to the segment CD because the two angles it creates (indicated in orange and blue) are each 90 degrees. The segment AB can be called the perpendicular from A to the segment CD, using «perpendicular» as a noun. The point B is called the foot of the perpendicular from A to segment CD, or simply, the foot of A on CD.[1]
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians). The condition of perpendicularity may be represented graphically using the perpendicular symbol, ⟂. It can be defined between two lines (or two line segments), between a line and a plane, and between two planes.
Perpendicularity is one particular instance of the more general mathematical concept of orthogonality; perpendicularity is the orthogonality of classical geometric objects. Thus, in advanced mathematics, the word «perpendicular» is sometimes used to describe much more complicated geometric orthogonality conditions, such as that between a surface and its normal vector.
Definitions[edit]
A line is said to be perpendicular to another line if the two lines intersect at a right angle.[2] Explicitly, a first line is perpendicular to a second line if (1) the two lines meet; and (2) at the point of intersection the straight angle on one side of the first line is cut by the second line into two congruent angles. Perpendicularity can be shown to be symmetric, meaning if a first line is perpendicular to a second line, then the second line is also perpendicular to the first. For this reason, we may speak of two lines as being perpendicular (to each other) without specifying an order.
Perpendicularity easily extends to segments and rays. For example, a line segment 


A line is said to be perpendicular to a plane if it is perpendicular to every line in the plane that it intersects. This definition depends on the definition of perpendicularity between lines.
Two planes in space are said to be perpendicular if the dihedral angle at which they meet is a right angle.
Foot of a perpendicular[edit]
The word foot is frequently used in connection with perpendiculars. This usage is exemplified in the top diagram, above, and its caption. The diagram can be in any orientation. The foot is not necessarily at the bottom.
More precisely, let A be a point and m a line. If B is the point of intersection of m and the unique line through A that is perpendicular to m, then B is called the foot of this perpendicular through A.
Construction of the perpendicular[edit]
Construction of the perpendicular (blue) to the line AB through the point P.
Construction of the perpendicular to the half-line h from the point P (applicable not only at the end point A, M is freely selectable), animation at the end with pause 10 s
To make the perpendicular to the line AB through the point P using compass-and-straightedge construction, proceed as follows (see figure left):
- Step 1 (red): construct a circle with center at P to create points A’ and B’ on the line AB, which are equidistant from P.
- Step 2 (green): construct circles centered at A’ and B’ having equal radius. Let Q and P be the points of intersection of these two circles.
- Step 3 (blue): connect Q and P to construct the desired perpendicular PQ.
To prove that the PQ is perpendicular to AB, use the SSS congruence theorem for QPA’ and QPB’ to conclude that angles OPA’ and OPB’ are equal. Then use the SAS congruence theorem for triangles OPA’ and OPB’ to conclude that angles POA and POB are equal.
To make the perpendicular to the line g at or through the point P using Thales’s theorem, see the animation at right.
The Pythagorean theorem can be used as the basis of methods of constructing right angles. For example, by counting links, three pieces of chain can be made with lengths in the ratio 3:4:5. These can be laid out to form a triangle, which will have a right angle opposite its longest side. This method is useful for laying out gardens and fields, where the dimensions are large, and great accuracy is not needed. The chains can be used repeatedly whenever required.
In relationship to parallel lines[edit]
The arrowhead marks indicate that the lines a and b, cut by the transversal line c, are parallel.
If two lines (a and b) are both perpendicular to a third line (c), all of the angles formed along the third line are right angles. Therefore, in Euclidean geometry, any two lines that are both perpendicular to a third line are parallel to each other, because of the parallel postulate. Conversely, if one line is perpendicular to a second line, it is also perpendicular to any line parallel to that second line.
In the figure at the right, all of the orange-shaded angles are congruent to each other and all of the green-shaded angles are congruent to each other, because vertical angles are congruent and alternate interior angles formed by a transversal cutting parallel lines are congruent. Therefore, if lines a and b are parallel, any of the following conclusions leads to all of the others:
- One of the angles in the diagram is a right angle.
- One of the orange-shaded angles is congruent to one of the green-shaded angles.
- Line c is perpendicular to line a.
- Line c is perpendicular to line b.
In computing distances[edit]
In geometry, the perpendicular distance between two objects is the distance from one to the other, measured along a line that is perpendicular to one or both.
The distance from a point to a line is the distance to the nearest point on that line. That is the point at which a segment from it to the given point is perpendicular to the line.
Likewise, the distance from a point to a curve is measured by a line segment that is perpendicular to a tangent line to the curve at the nearest point on the curve.
The distance from a point to a plane is measured as the length from the point along a segment that is perpendicular to the plane, meaning that it is perpendicular to all lines in the plane that pass through the nearest point in the plane to the given point.
Other instances include:
- Point on plane closest to origin, for the perpendicular distance from the origin to a plane in three-dimensional space
- Nearest distance between skew lines, for the perpendicular distance between two non-parallel lines in three-dimensional space
Perpendicular regression fits a line to data points by minimizing the sum of squared perpendicular distances from the data points to the line.
Other geometric curve fitting methods using perpendicular distance to measure the quality of a fit exist, as in total least squares.
The concept of perpendicular distance may be generalized to
- orthogonal distance, between more abstract non-geometric orthogonal objects, as in linear algebra (e.g., principal components analysis);
- normal distance, involving a surface normal, between an arbitrary point and its foot on the surface. It can be used for surface fitting and for defining offset surfaces.
Graph of functions[edit]
In the two-dimensional plane, right angles can be formed by two intersected lines if the product of their slopes equals −1. Thus defining two linear functions: y1 = a1x + b1 and y2 = a2x + b2, the graphs of the functions will be perpendicular and will make four right angles where the lines intersect if a1a2 = −1. However, this method cannot be used if the slope is zero or undefined (the line is parallel to an axis).
For another method, let the two linear functions be: a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0. The lines will be perpendicular if and only if a1a2 + b1b2 = 0. This method is simplified from the dot product (or, more generally, the inner product) of vectors. In particular, two vectors are considered orthogonal if their inner product is zero.
In circles and other conics[edit]
Circles[edit]
Each diameter of a circle is perpendicular to the tangent line to that circle at the point where the diameter intersects the circle.
A line segment through a circle’s center bisecting a chord is perpendicular to the chord.
If the intersection of any two perpendicular chords divides one chord into lengths a and b and divides the other chord into lengths c and d, then a2 + b2 + c2 + d2 equals the square of the diameter.[4]
The sum of the squared lengths of any two perpendicular chords intersecting at a given point is the same as that of any other two perpendicular chords intersecting at the same point, and is given by 8r2 – 4p2 (where r is the circle’s radius and p is the distance from the center point to the point of intersection).[5]
Thales’ theorem states that two lines both through the same point on a circle but going through opposite endpoints of a diameter are perpendicular. This is equivalent to saying that any diameter of a circle subtends a right angle at any point on the circle, except the two endpoints of the diameter.
Ellipses[edit]
The major and minor axes of an ellipse are perpendicular to each other and to the tangent lines to the ellipse at the points where the axes intersect the ellipse.
The major axis of an ellipse is perpendicular to the directrix and to each latus rectum.
Parabolas[edit]
In a parabola, the axis of symmetry is perpendicular to each of the latus rectum, the directrix, and the tangent line at the point where the axis intersects the parabola.
From a point on the tangent line to a parabola’s vertex, the other tangent line to the parabola is perpendicular to the line from that point through the parabola’s focus.
The orthoptic property of a parabola is that If two tangents to the parabola are perpendicular to each other, then they intersect on the directrix. Conversely, two tangents which intersect on the directrix are perpendicular. This implies that, seen from any point on its directrix, any parabola subtends a right angle.
Hyperbolas[edit]
The transverse axis of a hyperbola is perpendicular to the conjugate axis and to each directrix.
The product of the perpendicular distances from a point P on a hyperbola or on its conjugate hyperbola to the asymptotes is a constant independent of the location of P.
A rectangular hyperbola has asymptotes that are perpendicular to each other. It has an eccentricity equal to 
In polygons[edit]
Triangles[edit]
The legs of a right triangle are perpendicular to each other.
The altitudes of a triangle are perpendicular to their respective bases. The perpendicular bisectors of the sides also play a prominent role in triangle geometry.
The Euler line of an isosceles triangle is perpendicular to the triangle’s base.
The Droz-Farny line theorem concerns a property of two perpendicular lines intersecting at a triangle’s orthocenter.
Harcourt’s theorem concerns the relationship of line segments through a vertex and perpendicular to any line tangent to the triangle’s incircle.
Quadrilaterals[edit]
In a square or other rectangle, all pairs of adjacent sides are perpendicular. A right trapezoid is a trapezoid that has two pairs of adjacent sides that are perpendicular.
Each of the four maltitudes of a quadrilateral is a perpendicular to a side through the midpoint of the opposite side.
An orthodiagonal quadrilateral is a quadrilateral whose diagonals are perpendicular. These include the square, the rhombus, and the kite. By Brahmagupta’s theorem, in an orthodiagonal quadrilateral that is also cyclic, a line through the midpoint of one side and through the intersection point of the diagonals is perpendicular to the opposite side.
By van Aubel’s theorem, if squares are constructed externally on the sides of a quadrilateral, the line segments connecting the centers of opposite squares are perpendicular and equal in length.
Lines in three dimensions[edit]
Up to three lines in three-dimensional space can be pairwise perpendicular, as exemplified by the x, y, and z axes of a three-dimensional Cartesian coordinate system.
See also[edit]
- Orthogonal projection
- Tangential and normal components
Notes[edit]
- ^ Kay (1969, p. 114)
- ^ Kay (1969, p. 91)
- ^ Kay (1969, p. 91)
- ^ Posamentier and Salkind, Challenging Problems in Geometry, Dover, 2nd edition, 1996: pp. 104–105, #4–23.
- ^ College Mathematics Journal 29(4), September 1998, p. 331, problem 635.
References[edit]
- Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble, LCCN 52-13504
- Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69-12075
External links[edit]
- Definition: perpendicular with interactive animation.
- How to draw a perpendicular bisector of a line with compass and straight edge (animated demonstration).
- How to draw a perpendicular at the endpoint of a ray with compass and straight edge (animated demonstration).
Значок перпендикулярности в ворде
Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).
В Word можно вставлять математические символы в уравнения и текст.
На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.
В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.
Щелкните стрелку рядом с названием набора символов, а затем выберите набор символов, который вы хотите отобразить.
Щелкните нужный символ.
Доступные наборы символов
В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.
Основные математические символы
Часто используемые математические символы, такие как > и
Вопрос решен и закрыт.
Лучший ответ
Енот 8 (337417) 6 26 633 6 лет
Ответы
FighteR (30) 7 (88378) 7 26 967 6 лет
ПРОЖЕКТОР 6 (9106) 3 13 43 6 лет
радует, что у некоторых очень не плохо развито ассоциативное мышление! Причем морфологически безупречное .))
Ylarya 6 (6586) 2 4 15 6 лет
Vadinho 6 (16535) 3 41 85 6 лет
Похожие вопросы
Это лого фирмы Ямаха. 3 скрещённых камертона (небольшой портативный прибор, точно и ясно издающий звук определённой высоты со слабыми гармоническими призвуками.)
Скорее всего на уроках музыки вам это рассказывали.
Для обозначения перпендикулярности имеется общепринятый символ: ⊥ <displaystyle perp > , предложенный в 1634 году французским математиком Пьером Эригоном. Например, перпендикулярность прямых m <displaystyle m> и n <displaystyle n> записывают как m ⊥ n <displaystyle mperp n> .
Содержание
На плоскости [ править | править код ]
Перпендикулярные прямые на плоскости [ править | править код ]
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.
Про прямую m <displaystyle m> перпендикулярную к прямой ℓ <displaystyle ell > проведённую через точку P <displaystyle P> вне прямой ℓ <displaystyle ell > , говорят, что m <displaystyle m> есть перпендикуляр опущенный из P <displaystyle P> на ℓ <displaystyle ell > . Если же точка P <displaystyle P> лежит на прямой ℓ <displaystyle ell > , то говорят, что m <displaystyle m> есть перпендикуляр к восстановленный из P <displaystyle P> к ℓ <displaystyle ell > (устаревший термин восставленный [1] ).
В координатах [ править | править код ]
В аналитическом выражении прямые, заданные линейными функциями
y = a ⋅ x + b <displaystyle y=acdot x+b>
y = k ⋅ x + m <displaystyle y=kcdot x+m>
будут перпендикулярны, если выполнено следующее условие на их угловые коэффициенты
a ⋅ k = − 1. <displaystyle acdot k=-1.>
Построение перпендикуляра [ править | править код ]
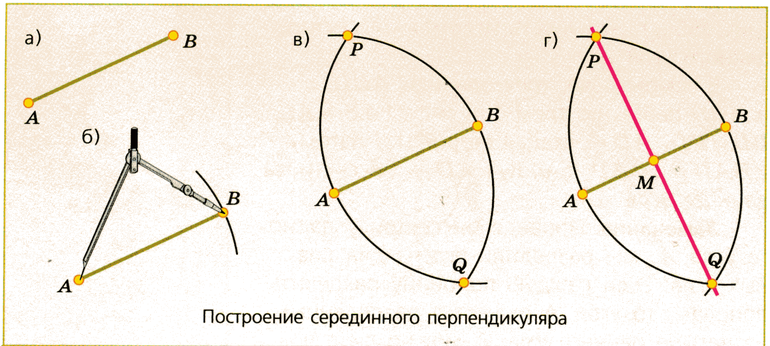
Шаг 1: С помощью циркуля проведём полуокружность с центром в точке P, получив точки А и В.
Шаг 2: Не меняя радиуса, построим две полуокружности с центром в точках A и В соответственно, проходящими через точку P. Кроме точки P есть ещё одна точка пересечения этих полуокружностей, назовём её Q.
Шаг 3: Соединяем точки P и Q. PQ и есть перпендикуляр к прямой AB.
Координаты точки основания перпендикуляра к прямой [ править | править код ]
Пусть прямая задаётся точками A ( x a , y a ) <displaystyle A(x_,y_)> и B ( x b , y b ) <displaystyle B(x_,y_)> . На прямую опускается перпендикуляр из точки P ( x p , y p ) <displaystyle P(x_
)> . Тогда основание перпендикуляра O ( x o , y o ) <displaystyle O(x_ ,y_ )> можно найти следующим образом.
Если x a = x b <displaystyle x_=x_> (вертикаль), то x o = x a <displaystyle x_ =x_> и y o = y p <displaystyle y_ =y_
> . Если y a = y b <displaystyle y_=y_> (горизонталь), то x o = x p <displaystyle x_ =x_
> и y o = y a <displaystyle y_ =y_> .
Во всех остальных случаях:
x o = x a ⋅ ( y b − y a ) 2 + x p ⋅ ( x b − x a ) 2 + ( x b − x a ) ⋅ ( y b − y a ) ⋅ ( y p − y a ) ( y b − y a ) 2 + ( x b − x a ) 2 <displaystyle x_ =<frac -y_)^<2>+x_
cdot (x_-x_)^<2>+(x_-x_)cdot (y_-y_)cdot (y_
-y_)><(y_-y_)^<2>+(x_-x_)^<2>>>> ; y o = ( x b − x a ) ⋅ ( x p − x o ) ( y b − y a ) + y p <displaystyle y_ =<frac <(x_ -x_)cdot (x_
В трёхмерном пространстве [ править | править код ]
Перпендикулярные прямые [ править | править код ]
Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим взаимно перпендикулярным прямым, лежащим в одной плоскости. Две прямые, лежащие в одной плоскости, называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.
Перпендикулярность прямой к плоскости [ править | править код ]
Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна всем прямым, лежащим в этой плоскости.
Признак: Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна этой плоскости.
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Перпендикулярные плоскости [ править | править код ]
Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.
- Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
- Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
- Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
- Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна их линии пересечения [2] .
В многомерных пространствах [ править | править код ]
Перпендикулярность плоскостей в 4-мерном пространстве [ править | править код ]
Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.
Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.
В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).
Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно ( 4 2 ) = 6 <displaystyle < binom <4><2>>=6> : xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).
Перпендикулярность прямой и гиперплоскости [ править | править код ]
Пусть задано n-мерное евклидово пространство R n <displaystyle mathbb ^ > (n>2) и ассоциированное с ним векторное пространство W n <displaystyle W^ > , а прямая l с направляющим векторным пространством L 1 <displaystyle L^<1>> и гиперплоскость Π k <displaystyle Pi _ > с направляющим векторным пространством L k <displaystyle L^ > (где L 1 ⊂ W n <displaystyle L_<1>subset W^ > , L k ⊂ W n , k n <displaystyle L^ subset W^ , k ) принадлежат пространству R n <displaystyle mathbb ^ > .
Прямая l называется перпендикулярной гиперплоскости Π k <displaystyle Pi _ > , если подпространство L 1 <displaystyle L_<1>> ортогонально подпространству L k <displaystyle L^ > , то есть ( ∀ a → ∈ L 1 ) ( ∀ b → ∈ L k ) a → b → = 0 <displaystyle (forall <vec >in L_<1>) (forall <vec >in L_ ) <vec ><vec >=0>
Как сделать вертикальный текст в Word — 5 способов
В процессе оформления документа в текстовом редакторе Microsoft Word пользователю может понадобиться сделать вертикальный текст в Ворде. Это необходимо, например, для печати вертикально расположенного текста или для оформления документа со сложной структурой.
В программе Word можно набирать текст, расположенный горизонтально или вертикально. В случае необходимости вы можете изменить горизонтальное расположение текста на вертикальное направление текста.
В связи с этим, у пользователей возникают вопросы о том, как сделать вертикальный текст в программе MS Word. Решить данную проблему можно несколькими способами.
В редакторе Word вертикальный текст можно напечатать следующими методами:
- вертикальный текст вводится в Ворде в таблице;
- вертикальное положение текста создается с помощью надписи;
- установка направления текста в формате фигуры;
- набор текста в столбик;
- использование шаблона рисунка в SmartArt.
Вы можете вставить текст с вертикальным направлением в любом месте документа Word, используя предложенные варианты.
В этом руководстве вы найдете инструкции о том, как расположить текст вертикально в документе, открытом в разных версиях программы Word. Необходимые действия выполняются подобным образом, имеются только некоторые отличия в интерфейсе приложения.
Как в таблице Ворд сделать текст вертикально
Использование таблицы — первое, что обычно рекомендуют пользователю, когда его интересует ответ на вопрос о том, как в Ворде сделать вертикальный текст. Это довольно простой способ для изменения направления текста в документе.
Выполните следующие действия:
- В окне открытого документа Word установите курсор мыши в том месте, где необходимо вывести вертикальное расположение текста.
- Войдите во вкладку «Вставка», а затем щелкните по кнопке «Таблица».
- В выпадающем меню нажмите на одну или несколько ячеек, в зависимости от того, сколько вертикальных надписей вам нужно сделать.
- В ячейке таблицы наберите необходимый текст.
- Нажмите на правую кнопку мыши, а в контекстном меню выберите пункт «Направление текста…».
- В окне «Направление текста – Ячейка таблицы», в группе «Ориентация» нажмите сначала на подходящий вариант размещения текста, а потом на «ОК».
- Потяните край таблицы за нижнюю линию, чтобы сузить и растянуть ее до нужного размера.
- Щелкните внутри таблицы правой кнопкой мыши.
- Выберите «Свойства таблицы…». В Word 2007-2010 можно сразу нажать на пункт «Границы и заливка…», потому что там есть такой пункт в контекстном меню.
- В окне «Свойства таблицы», во вкладке «Таблица» нажмите на кнопку «Границы и заливка…».
- В окне «Границы и заливка», во вкладке «Граница», в опции «Тип:» нажмите на «Нет».
- Подтвердите свои действия нажатием на кнопку «ОК».
- В результате, у вас появилось вертикальное направление текста в Ворде без границы таблицы.
Как в Ворде написать текст вертикально с помощью функции «Надпись»
Сейчас мы разберем, как написать текст вертикально, используя функцию «Надпись». Этот простой способ поможет вам быстро вставить в документ необходимый текст в вертикальном положении.
Пройдите несколько последовательных шагов:
- Откройте вкладку «Вставка».
- В группе «Текст» нажмите на кнопку «Текстовое поле».
- В открывшемся меню выберите «Простая надпись».
- В окне документа появиться текстовое поле с надписью по умолчанию.
- Нажмите на клавишу «Del» (Delete) для удаления имеющегося текста.
- Напишите там свой текст.
- Кликните по краю границы, а затем с помощью кнопки с поворотом вручную поверните текст как вам нужно.
Выполняя подобную операцию с использованием функции надписи, вы можете повернуть текст автоматически, а не вручную.
- После создания надписи войдите во вкладку «Формат фигуры» («Формат»).
- В группе «Текст» нажмите на значок «Направление текста».
- Выберите вариант: «Повернуть на 90°» или «Повернуть на 270°». В зависимости от выбранного варианта, текст надписи расположится сверху вниз или снизу вверх.
- Чтобы удалить контур надписи, кликните по значку «Контур фигуры» в группе «Стили фигур», а выпадающем меню нажмите «Нет контура».
Указываем направление текста в макете фигуры
Похожий на предыдущий способ предполагает использование формата фигуры, в которой набирается нужный вам текст.
- Из меню «Вставка» в группе «Текст» нажмите на «Текстовое поле».
- В открывшемся меню нажмите на пункт «Добавление надписи».
- С помощью указателя мыши начертите контур, в который нужно будет вставить текст.
- Напишите необходимый текст.
- Щелкните по краю контура, а в контекстном меню нажмите «Формат фигуры…».
- В области «Формат фигуры», в разделе «Параметры фигуры» («Макет фигуры») нажмите на кнопку «Макет и свойства».
- В опции «Надпись», в параметре «Направление текста» укажите: «Повернуть на 270°» или «Повернуть на 90°».
- Отрегулируйте правильное отображение текста по высоте и ширине.
- Кликните по границе контура.
- В открывшемся меню нажмите на «Контур», выберите параметр «Нет контура».
Как сделать направление текста в Ворде вертикально в SmartArt
Этот способ подходит, если вам нужно добавить в документ Word вертикальный текст, помещенный в какой-нибудь рисунок с готовым блоком. В этом случае, мы используем графические объекты SmartArt.
- Войдите во вкладку «Вставка», в группе «Иллюстрации» нажмите на кнопку «SmartArt».
- В окне «Выбор рисунка SmartArt» выберите «Простой блочный список» или другой подходящий вариант.
- Введите нужный текст в выбранную фигуру.
- Щелкните правой кнопкой мыши, в открывшемся меню нажмите на пункт «Формат фигуры…».
- В области «Формат фигуры» откройте «Параметры текста», а в опции «Направление текста» установите значение поворота.
- Подгоните текст по масштабу, в случае необходимости измените размер шрифта.
- Удалите из документа остальные фигуры, если они не нужны, используя функцию «Вырезать».
Как расположить текст вертикально столбиком в Ворде
Данный метод не самый подходящий для наших целей, но есть и такой вариант, который можно использовать. Суть метода в том, чтобы вводить по одной букве с новой строки, постепенно набирая наше выражение в столбик. Затем нужно будет изменить междустрочный интервал между отдельными буквами набранного текста, чтобы привести его в более подходящий вид.
Проделайте следующие действия:
- Набирайте по одной букве из слова или словосочетания, а затем сразу нажимайте на клавишу «Enter».
- Введите следующую букву с новой строчки, и так далее.
- После того, как текст расположился столбиком, нам необходимо сократить межстрочные интервалы, чтобы привести его в более благоприятный вид.
- В группе «Абзац» нажмите на кнопку «Интервал».
- В открывшемся меню нажмите на пункт «Другие варианты междустрочных интервалов…».
- В окне «Абзац», во вкладке «Отступы и интервалы», перейдите к группе «Интервал», а в параметре «междустрочный:» установите соответствующее значение. Опытным путем выяснилось, что без искажений исходного текста подходит величина не ниже «0,7».
- Нажмите на кнопку «ОК».
Выводы статьи
В процессе редактирования некоторым пользователям необходимо узнать о том, как сделать вертикальное направление текста в документе Word. Это бывает нужно для оформления или форматирования документа. Существует несколько способов с помощью которых пользователь может расположить вертикальный текст в необходимом месте редактируемого документа, открытого в программе Microsoft Word.
Где взять символы для «Ворда» и как их вставить в текст
При наборе текста в программе «Майкрософт Ворд» многие пользователи испытывают потребность во вставке специального символа и знака, но не каждый знает, как это сделать. Забегая вперед, скажем, что существует не один способ выполнения поставленной задачи. В статье будет представлено шесть самых известных и легко выполнимых.
Способ 1: таблица символов в программе
Сейчас будет разобран самый традиционный метод, как вставить символ в «Ворде». Подразумевает он использование встроенной в программу утилиты «Таблица символов». Итак, вот что необходимо сделать, чтобы открыть ее:
- Откройте программу и перейдите во вкладку под названием «Вставка».
- На панели инструментов отыщите группу «Символы», где нажмите по кнопке «Символ».
- В появившемся подменю выберите строку «Другие символы».
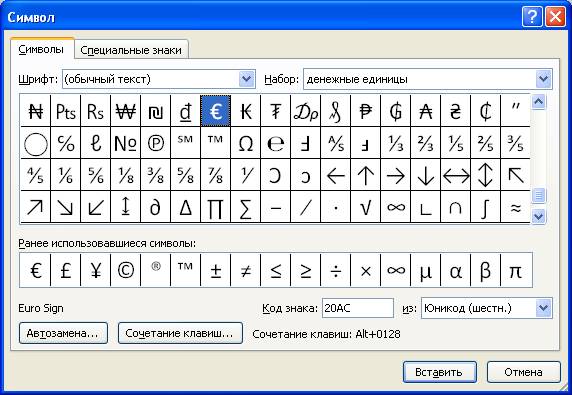
После выполнения этих действий появится новое окно с соответствующим названием. В нем вы можете найти практически все известные символы и знаки. Для быстрой навигации вы можете выбрать отдельный набор из одноименного выпадающего списка. Теперь давайте разберемся, как произвести вставку символа евро. Его мы будем использовать в качестве примера.
- В выпадающем списке «Набор» выберите «Денежные единицы».
- Среди всех прочих знаков отыщите символ евро и выделите его.
- Нажмите кнопку «Вставить».
После этого выбранный символ будет вставлен в текст. Обратите внимание, что вписывается он непосредственно в то место, где был установлен курсор, поэтому предварительно установите его в нужную часть текста.
Способ 2: горячие клавиши
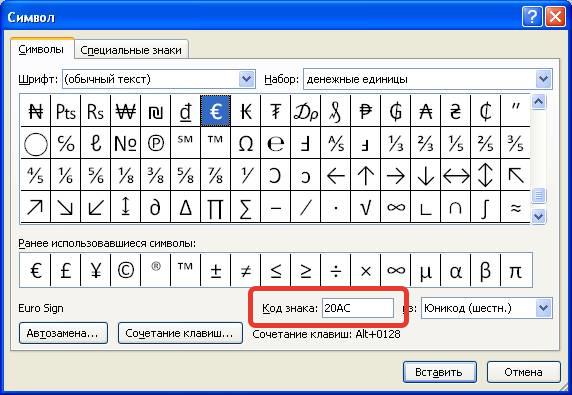
Первый способ, как вставить символ в «Ворде», некоторым может показаться слишком долгим, ведь необходимо проделать немало действий, чтобы выполнить вставку интересующего символа. Куда проще и быстрее будет использовать для этих целей специальные горячие клавиши. Все, что необходимо знать, — это специальный код нужного символа. Чтобы его посмотреть, необходимо в «Таблице символов» выделить нужный знак и обратить внимание на поле «Код знака», именно там и расположен нужный код.
Чтобы вставить символ с помощью горячих клавиш, необходимо:
- Поставить курсор в ту часть текста, где будет произведена вставка.
- Ввести код, например, символа евро — 20AC.
- Нажать клавиши Alt+X.
После этого код будет заменен на знак евро.
Способ 3: таблица символов на компьютере
Есть «Таблица символов» для «Ворда», но также на компьютере есть ее аналог, который носит такое же название. С его помощью без труда удастся вставить необходимый знак как в текстовом редакторе, так и в любом другом текстовом поле. Для начала рассмотрим, как запустить эту утилиту:
- Откройте меню «Пуск».
- Перейдите в меню всех приложений.
- Отыщите папку «Стандартные» и откройте ее.
- В ней запустите приложение «Таблица символов».
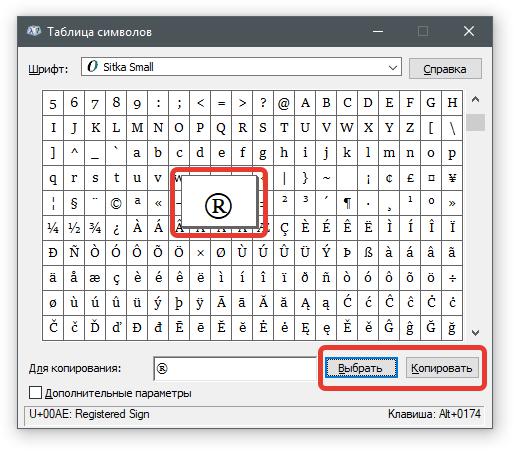
Итак, таблица запущена, можно переходить непосредственно к вставке необходимого символа.
- В списке всех символов выделите необходимый.
- Нажмите кнопку «Выбрать».
- Если вам необходимо вставить несколько символов подряд, то можете таким же образом добавить еще.
- Нажмите кнопку «Копировать», чтобы поместить выбранные символы в буфер обмена.
- Установите курсор в текстовое поле, в ту часть, куда нужно вставить символы.
- Нажмите ПКМ и выберите опцию «Вставить».
Также заметьте, что в таблице можно выбирать шрифты. Если текстовое поле поддерживает данное форматирование, то в него будет вставлен символ выбранного вами шрифта.
Способ 4: альт-коды
Как было уже выяснено, символы для «Ворда» можно брать за пределами самой программы. Сейчас будет рассказано об альт-кодах и том, как ими пользоваться. Но сразу стоит пояснить, что данный метод работает лишь на операционных системах под руководством Windows.
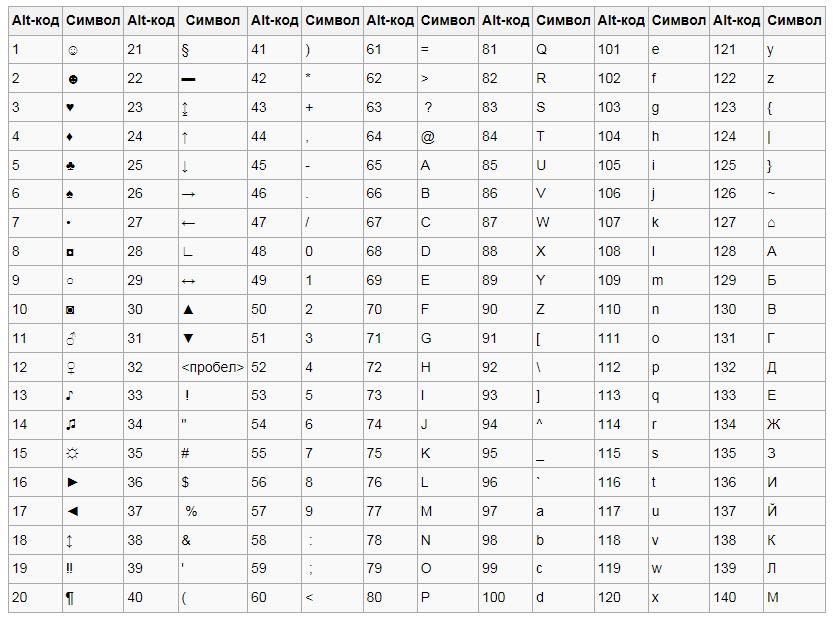
Итак, у каждого символа есть собственный код, зная который, можно выполнить его вставку в любое место текста. Полный перечень кодов знаков вы можете посмотреть в «Википедии», мы же рассмотрим принцип их использования. Например, вы решили вставить символ «Стрелка» в «Ворде», код которого — «26». Чтобы произвести вставку, вам необходимо:
- Зажать и удерживать клавишу Alt, находящуюся в левой части клавиатуры.
- Ввести код символа, в данном примере — «26».
- Отпустить клавишу Alt.
После этого на месте курсора появится выбранный вами знак.
Способ 5: таблица символов в интернете
Для «Ворда» символы можно брать из таблицы в интернете. Например, для этого подойдет сайт unicode-table.com. Пользоваться данным способом так же просто, как третьим. Вот что вам нужно:
- Откройте сайт с таблицей символов.
- Выберите из огромного списка необходимый вам знак.
- Нажмите кнопку «Копировать», чтобы поместить его в буфер обмена.
- Установите курсор в ту часть текста, куда необходимо вставить символ.
- Нажмите ПКМ и выберите из меню «Вставить».
Символ будет вставлен.
Способ 6: обычное копирование
Было уже разобрано пять способов, как вставить символ в «Ворде». Некоторые из них подходят даже для вставки вне рамок приведенной программы. К ним относится и этот. По названию раздела уже можно догадаться, что данный метод подразумевает использование опции обычного копирования. То есть вам необходимо:
- Зажав ЛКМ, выделить в тексте нужный вам символ.
- Нажать ПКМ и выбрать опцию «Копировать».
- Установить курсор в ту часть текста, куда предполагается осуществить вставку скопированного символа.
- Нажать ПКМ и выбрать «Вставить».
Конечно, этот метод не самый лучший, но если вы делаете рерайт какого-то текста, и вам необходимо написать символ, который есть в нем, то куда проще и быстрей будет сделать это именно таким способом.
Заключение
В завершение статьи скажем, что символы для «Ворда» могут браться не только из предустановленных приложений и утилит, но и со сторонних ресурсов. Например, со специального сайта, который был представлен в пятом способе, или вообще из случайного текста в Сети или на компьютере, как было продемонстрировано в шестом методе. Надеемся, статья помогла вам в решении поставленной задачи.
Пишем символы на клавиатуре
Иногда возникает ситуация, когда вам необходимо употребить в каком-нибудь тексте специальный символ, однако на клавиатуре клавиши с таким символом не существует. Что тогда?
Существует несколько путей.
Если вы печатаете в текстовом редакторе Microsoft Word 2007, то все просто: достаточно выбрать на закладке Вставка пункт “Символ”. В раскрывшемся списке выбираете нужный символ либо нажимаете на Другие символы… В открывшемся диалоговом окне находите необходимый символ и нажимаете клавишу Вставить.
А как поступить с другими редакторами или поисковиками?
Вот коды некоторых символов.
●Пошагово:
1.Включаем кнопку NumLock(в правой части клавиатуры)
2. Зажимаем Alt.
3. И одновременно с зажатой клавишей alt Набираем на цифровом блоке комбинацию.
4. Отжимаем Alt.
4. Любуемся значком.
Еще символы:
© Копирайт [0169]♥ Сердечко [3]® Зарезервировано [0174]℠ Знак обслуживания [8480]℃ Цельсий [8451]℅ C/о [8453]℉ Фаренгейт [8457]№ Номерной знак [8470]℗ Копирайт записи [8471]℞ Фармацевтический символ [8478]Ω Ом [8486]℧ Перевернутый Ом [8487]☀ Солнце [9728]☁ Туча [9729]☂ Зонтик [9730]☃ Снеговик [9731]☄ Комета [9732]★ Звезда (закрашенная) [9733]☆ Звезда (контуры) [9734]☇ Молния [9735]☈ Гроза [9736]☉ Солнце (контур) [9737]☊ Восходящий узел [9738]☋ Нисходящий узел [9739]☌ Сопряжение [9740]☍ Оппозиция [9741]☎ Телефон (закрашенный) [9742]☏ Телефон (контур) 9743]☐ Пустой квадрат [9744]☑ Квадратик с галочкой [9745]☒ Квадратик с крестиком X [9746]☓ Андреевский крест [9747]☚ Палец, показывающий налево (закрашенный) [9754]☛ Палец, показывающий направо (закрашенный) [9755]☜ Палец, показывающий налево (контур) [9756]☝ Палец, показывающий вверх (контур) [9757]☞ Палец, показывающий направо (контур) [9758]☟ Палец, показывающий вниз (контур) [9759]☠ Череп и кости [9760]☡ Предупреждающий знак [9761]☢ Знак радиации [9762]☣ Знак биологической опасности [9763]☤ Кадуцей (жезл Гермеса) [9764]☥ Анкх [9765]☦ Восточно-христианский крест [9766]☧ Христограмма [9767]☨ Патриархальный крест [9768]☩ Греческий крест [9769]☪ Луна и звезда [9770]☫ Символ Фарси [9771]☬ Ади Шакти [9772]☭ Серп и молот [9773]☮ Знак мира [9774]☯ Инь и Янь [9775]☰ Триграмма небо [9776]☱ Триграмма озеро [9777]☲ Триграмма огонь [9778]☳ Триграмма гроза [9779]☴ Триграмма ветер [9780]☵ Триграмма вода [9781]☶ Триграмма гора [9782]☷ Триграмма земля [9783]☸ Колесо дхарма [9784]☹ Грустный смайл [9785]☺ Веселый смайл [9786]☻ Черный смайл [9787]☽ Растущая луна [9789]☾ Спадающая луна [9790]☿ Меркурий [9791]♀ Венера (знак женщины) [9792]♁ Земля [9793]♂ Марс (знак мужчины) [9794]♃ Юпитер [9795]♄ Сатурн [9796]♅ Уран [9797]♆ Нептун [9798]♇ Плутон [9799]♈ Овен [9800]♉ Телец [9801]♊ Близнецы [9802]♋ Рак [9803]♌ Лев [9804]♍ Дева [9805]♎ Весы [9806]♏ Скорпион [9807]♐ Стрелец [9808]♑ Козерог [9809]♒ Водолей [9810]♓ Рыбы [9811]♔ Белый король [9812]♕ Белая королева [9813]♖ Белая ладья [9814]♗ Белый слон [9815]♘ Белая лошадь [9816]♙ Белая пешка [9817]♚ Черный король [9818]♛ Черная королева [9819]♜ Черная ладья [9820]♝ Черный слон [9821]♞ Черная лошадь [9822]♟ Черная пешка [9823]♠ Черная пика [9824]♡ Черва [9825]♢ Бубна [9826]♣ Трефа [9827]♤ Пика (контур) [9828]♥ Черва (закрашенная) или сердце [9829]♦ Бубна (закрашенная) [9830]♧ Трефа (контур) [9831]♨ Гейзер [9832]♩ Музыкальная четвертная нота [9833]♪ Музыкальная восьмая нота [9834]♫ Соединенные две ноты [9835]♬ Соединенные двойной планкой две ноты [9836]♭ Бемоль [9837]♮ Звук натурального звукоряда [9838]♯ Диез [9839]✁ Отрезать сверху [9985]✂ Отрезать здесь [9986]✃ Отрезать снизу [9987]✄ Ножницы [9988]✆ Общественный телефон [9990]✇ Кассета [9991]✈ Аэропорт/самолет [9992]✉ Конверт/email [9993]✌ Знак победы [9996]✍ Подпись [9997]✎ Диагональный карандаш [9998]✏ Карандаш [9999]✐ Диагональный карандаш, смотрящий вверх [10000]✓ Галочка [10003]✔ Жирная галочка [10004]✕ Знак умножения/X [100005]✖ Жирный знак умножения/X [10006]✗ Наклоненный знак X [10007]✘ Жирный наклоненный знак X [10008]✝ Римский крест [10013]✞ Римский крест 3D [10014]✟ Латинский крест (контур) [10015]✠ Мальтийский крест [10016]✡ Звезда Давида [10017]❛ Знак кавычек [10075]❜ Знак кавычек (перевернутый) [10076]❝ Двойной знак кавычек [10077]❞ Двойной знак кавычек (перевернутый) [10078]™ Товарный знак [0153]○= 777
Не забывайте подписываться и делиться с друзьями ссылкой на наш канал. Самое интересное впереди.
Источник статьи: http://zen.yandex.ru/media/goodtip/pishem-simvoly-na-klaviature-5ba8ef802098b300aab5f80a
Значок перпендикулярности в ворде
Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).
В Word можно вставлять математические символы в уравнения и текст.
На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.
В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.
Щелкните стрелку рядом с названием набора символов, а затем выберите набор символов, который вы хотите отобразить.
Доступные наборы символов
В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.
Основные математические символы
Часто используемые математические символы, такие как > и
Лучший ответ
Енот 8 (337417) 6 26 633 6 лет
Ответы
FighteR (30) 7 (88378) 7 26 967 6 лет
ПРОЖЕКТОР 6 (9106) 3 13 43 6 лет
радует, что у некоторых очень не плохо развито ассоциативное мышление! Причем морфологически безупречное .))
Ylarya 6 (6586) 2 4 15 6 лет
Vadinho 6 (16535) 3 41 85 6 лет
Похожие вопросы
Это лого фирмы Ямаха. 3 скрещённых камертона (небольшой портативный прибор, точно и ясно издающий звук определённой высоты со слабыми гармоническими призвуками.)
Скорее всего на уроках музыки вам это рассказывали.
Для обозначения перпендикулярности имеется общепринятый символ: ⊥ 



Содержание
На плоскости [ править | править код ]
Перпендикулярные прямые на плоскости [ править | править код ]
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.
Про прямую m 











В координатах [ править | править код ]
В аналитическом выражении прямые, заданные линейными функциями
y = a ⋅ x + b
y = k ⋅ x + m
будут перпендикулярны, если выполнено следующее условие на их угловые коэффициенты
a ⋅ k = − 1.
Построение перпендикуляра [ править | править код ]
Шаг 1: С помощью циркуля проведём полуокружность с центром в точке P, получив точки А и В.
Шаг 2: Не меняя радиуса, построим две полуокружности с центром в точках A и В соответственно, проходящими через точку P. Кроме точки P есть ещё одна точка пересечения этих полуокружностей, назовём её Q.
Шаг 3: Соединяем точки P и Q. PQ и есть перпендикуляр к прямой AB.
Координаты точки основания перпендикуляра к прямой [ править | править код ]
Пусть прямая задаётся точками A ( x a , y a ) 



Если x a = x b 

> 

> 

Во всех остальных случаях:
x o = x a ⋅ ( y b − y a ) 2 + x p ⋅ ( x b − x a ) 2 + ( x b − x a ) ⋅ ( y b − y a ) ⋅ ( y p − y a ) ( y b − y a ) 2 + ( x b − x a ) 2 = +x_
-y_)> +(x_-x_)^ >>> 
> 
В трёхмерном пространстве [ править | править код ]
Перпендикулярные прямые [ править | править код ]
Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим взаимно перпендикулярным прямым, лежащим в одной плоскости. Две прямые, лежащие в одной плоскости, называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.
Перпендикулярность прямой к плоскости [ править | править код ]
Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна всем прямым, лежащим в этой плоскости.
Признак: Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна этой плоскости.
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Перпендикулярные плоскости [ править | править код ]
Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.
- Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
- Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
- Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
- Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна их линии пересечения [2] .
В многомерных пространствах [ править | править код ]
Перпендикулярность плоскостей в 4-мерном пространстве [ править | править код ]
Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.
Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.
В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).
Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно ( 4 2 ) = 6 >=6> 
Перпендикулярность прямой и гиперплоскости [ править | править код ]
Пусть задано n-мерное евклидово пространство R n ^ > 







Прямая l называется перпендикулярной гиперплоскости Π k > 



Источник статьи: http://pcznatok.ru/kompjutery/znachok-perpendikuljarnosti-v-vorde.html
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Перпендикулярные прямые
Перпендикулярные прямые — это прямые, которые при пересечении образуют четыре прямых угла (Рис.1).
Перпендикулярность прямых обозначают специальным символом — 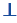
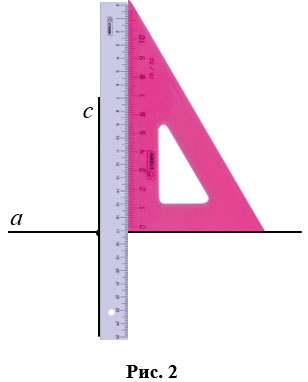
Чтобы начертить перпендикулярные прямые, используют чертежный угольник и линейку (Рис.2). С помощью линейки проводят прямую 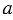
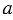
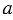
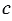
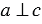
Свойство перпендикулярных прямых:
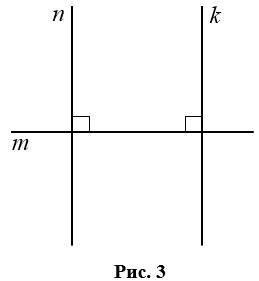
Если две прямые перпендикулярны к третьей, то они не пересекаются.
На Рис.3 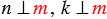
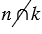
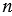
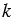
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точки, прямые, отрезки
Провешивание прямой на местности
Луч
Угол
Равенство геометрических фигур
Сравнение отрезков
Сравнение углов
Длина отрезка
Единицы измерения длины, расстояний
Градусная мера угла
Измерение углов на местности
Смежные углы
Вертикальные углы
Построение прямых углов на местности
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 214,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 17,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 334,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 436,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 444,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 669,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1076,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1281,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1297,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1303,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Перпендикуля́рность — бинарное отношение между различными объектами (векторами, прямыми, подпространствами и т. д.) в евклидовом пространстве. Частный случай ортогональности.
Содержание
- 1 На плоскости
- 1.1 Перпендикулярные прямые
- 1.2 Построение перпендикуляра
- 1.3 Координаты точки основания перпендикуляра к прямой
- 2 В трёхмерном пространстве
- 2.1 Перпендикулярные прямые
- 2.2 Перпендикулярность прямой и плоскости
- 2.3 Перпендикулярные плоскости
- 3 В многомерных пространствах
- 3.1 Перпендикулярность плоскостей в 4-мерном пространстве
- 3.2 Перпендикулярность прямой и гиперплоскости
- 3.3 Перпендикулярные гиперплоскости
- 4 См. также
- 5 Примечания
На плоскости
Перпендикулярные прямые
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.
В аналитическом выражении прямые, заданные линейными функциями 




Для обозначения перпендикулярности имеется общепринятый символ: 
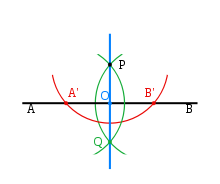
Построение перпендикуляра
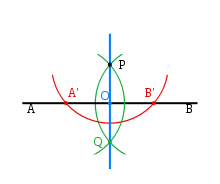
Построение перпендикуляра
Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А’ и В’.
Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A’ и В’ соответственно, проходящими через точку Р. Кроме точки Р есть ещё одна точка пересечения этих полуокружностей, назовём её Q.
Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ.
Координаты точки основания перпендикуляра к прямой
A(xa,ya) и B(xb,yb) — прямая, O(xo,yo) — основание перпендикуляра, опущенного из точки P(xp,yp).
Если xa = xb (вертикаль), то xo = xa и yo = yp. Если ya = yb (горизонталь), то xo = xp и yo = ya.
Во всех остальных случаях
- xo = (xa*(yb-ya)^2 + xp*(xb-xa)^2 + (xb-xa) * (yb-ya) * (yp-ya)) / ((yb-ya)^2+(xb-xa)^2);
- yo = (yb-ya)*(xo-xa)/(xb-xa)+ya.
В трёхмерном пространстве
Перпендикулярные прямые
Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим прямым, лежащим в одной плоскости и перпендикулярным в ней.
Перпендикулярность прямой и плоскости
Определение: Прямая называется перпендикулярной плоскости, если она перпендикулярна всем прямым лежащим в этой плоскости.
Признак: Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Перпендикулярные плоскости
Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.
- Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
- Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
- Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
- Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна их линии пересечения[1].
В многомерных пространствах
Перпендикулярность плоскостей в 4-мерном пространстве
Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.
Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.
В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).
Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно 
Перпендикулярность прямой и гиперплоскости
Пусть задано n-мерное евклидово пространство 







Прямая l называется перпендикулярной гиперплоскости 


Перпендикулярные гиперплоскости
См. также
- Параллельность
- Ортогональность
- Высота
- Теорема о трёх перпендикулярах
- N-мерная евклидова геометрия
Примечания
- ↑ Александров А.Д., Вернер А. Л., Рыжик В.И. Стереометрия. Геометрия в пространстве. — Висагинас: Alfa, 1998. — С. 46. — 576 с. — (Библиотека школьника). — ISBN 9986582539
Основные свойства
При рассмотрении того, какие прямые называют перпендикулярными, нужно уделить внимание свойствам. Они выглядят следующим образом:
- Через одну точку А можно провести только одну перпендикулярную линию основному отрезку, остальные линии будут наклонными и могут скрещиваться.
- Несколько перпендикуляров никогда не будут между собой пересекаться.
Для обозначения перпендикуляра применяется знак «⊥». В подобном случае угол составляет 90°. На чертеже пересечение обозначается своеобразным квадратом, которые рисуется от двух пересекающихся линий.
Доказательство взаимного расположения
Рассматриваемый термин получил широкое распространение, он фигурирует практически в каждой геометрической задаче. В некоторых случаях о взаимном расположении известно, в других это нужно доказать. Задача доказательства заключается в определении прямого угла между двумя прямыми или плоскостями. Необходимое и достаточное условие перпендикулярности заключается в теореме:
- Прямые взаимно перпендикулярны в случае, если направляющие векторы прямых перпендикулярны.
- Доказательство связано с определением направления векторов, любой должен быть перпендикулярен.
Для определения расположения плоскостей или отрезков относительно друг друга следует провести геометрическое построение. Проходить отрезки должны в одной точке.
Определение перпендикулярности прямой и плоскости
Рассматривая определение перпендикулярных прямых следует учитывать, что подобное свойство применимо к плоскости. Основной признак заключается в перпендикулярности отрезка к любому другому, который находится в плоскости. Перпендикулярность прямых в пространстве указывается определенным знаком.
Доказать перпендикулярность можно проведя геометрические построения. Признаки расположения плоскости и прямой под углом 90° заключаются в следующем:
- Если прямая перпендикулярна плоскости, то в ней можно отложить другую прямую, лежащую под углом 90°.
- В одной точке под прямым углом может пересекаться только две линии, значит, будет лежать только одна плоскость.
Отрезки могут быть также параллельными. В этом случае нет точки, в которой будут они пересекаться.
Построение перпендикуляра
Выдержать угловой коэффициент можно различным образом. В большинстве случаев для этого нужно иметь при себе циркуль. Построить перпендикуляр можно следующим образом:
- С помощью циркуля проводится построение полуокружности с центром в точке Х. На основном отрезке в результате этого получается две точки А и В. Для отображения полуокружности применяется другой цвет, полученная линия вспомогательная, поэтому не выделяется жирным.
- С точки А и В проводится откладывание двух полуокружностей, пересекающихся в двух местах по касательной. Данные точки (P и Q) используются для откладывания линии, которая может пересечь их и основной отрезок с ранее отложенными точками А и В.
Существенно упростить задачу можно путем применения специального чертежного инструмента, к примеру, любого прямоугольного треугольника. Он может называться угольником, основной его признак заключается в наличии двух перпендикулярных плоскостей. Построение проводится следующим образом:
- Одна из сторон, смежная с прямым углом, прикладывается к проведенному отрезку. На этом этапе главное — правильно совместить поверхность инструмента с ранее отложенной линией. Незначительное отклонение может привести к изменению угла.
- Проводится откладывание вертикального отрезка.
В геометрии чаще всего применяется именно второй способ. Однако первый урок позволяет начертить два взаимно перпендикулярных отрезка с высокой точностью. Недостаток применения циркуля заключается в наличии вспомогательных линий, которые стереть сложно. Написать о взаимном расположении линий можно в описательной записке.
Трехмерное пространство
В начертательной геометрии линии всегда находятся в двухмерном пространстве. В специальных программах можно начертить отрезки в трехмерном пространстве. Подобное взаимное расположение может выглядеть следующим образом:
- Два отрезка перпендикулярны относительно друг друга в случае, если они параллельны другим взаимно перпендикулярным линиям, лежащим в одной плоскости.
- Показать правильное взаимное расположение можно путем обозначения угла. Для этого применяются различные способы.
- Если две линии лежат в одной плоскости, то они взаимно перпендикулярны при образовании четырех прямых углов.
В жизни подобное расположение прямых встречается крайне часто. Проверить угол можно при применении специальных инструментов.
Четырехмерная система координат и лемма
Некоторые программы работают с четырехмерным пространством. Взаимное расположение плоскостей под прямым углом в этом случае имеет два смысла: они могут быть перпендикулярны в трехмерном смысле при образовании двугранного угла 90°.
Рассматриваться взаимное расположение плоскостей может и в 4-мерном смысле. Условия выглядят следующим образом:
- Они должны пересекаться в точке.
- Любые две линии, проведенные в плоскостях через точку пересечения также могут быть перпендикулярными.
Условия четырехмерного пространства определяют то, что через одну точку можно провести 6 взаимно перпендикулярных плоскостей. Определять их взаимное расположение можно несколькими различными способами.
Лемма, касающаяся перпендикулярности, связана с определением параллельности. Если одна из параллельных линий расположена под прямым углом относительно плоскости или отрезка, то вторая также перпендикулярна. Ответ на многие задачи связан с доказательством леммы:
- Даны два параллельных отрезка а и b, а также с. Задача заключается в доказательстве b ⊥ c при условии, что a ⊥ c.
- Через произвольную точку М проводится третий и четвертый отрезок, которые параллельны прямой а и с. Образующийся угол АМС равен 90°.
- Параллельны b и a при условии, что третий дополнительный отрезок параллелен отрезку а. В этом случае он будет параллелен и b.
При соблюдении условий полученный угол будет являться прямым. С учетом проведенных построений можно сформулировать определение перпендикулярности параллельных отрезков.
Применение термина
Как ранее было отмечено, встречается большое количество примеров применения рассматриваемого термина. На основе теоремы и доказательства были созданы различные формулы, позволяющие определить протяженность одного из сторон геометрической фигуры.
В средних и старших классах встречается большое количество задач, связанных с определением угла и протяженности сторон построенной фигуры. В некоторых случаях проводится построение диагонали, которая делит 90° на две равные части.
В жизни взаимное перпендикулярное расположение плоскостей встречается крайне часто. Примером служат несущие элементы различных сооружений. Подобное расположение позволяет правильно распределить оказываемую нагрузку. Править наклон можно путем применения специальных измерительных инструментов.
Многие геометрические фигуры построены на основе перпендикулярного расположения отрезков. Наиболее распространен параллелограмм или квадрат, треугольник. За счет выдерживания правильного угла обеспечивается также взаимное параллельное расположение сторон.
Приведенная выше информация указывает на то, что определение угла, под которым расположены плоскости, проводится в самых различных сферах. Инженеры и строители должны с высокой точностью контролировать этот показатель.