«÷» redirects here. For the music album of this name, see ÷ (album). For the Tifinagh character, see ⴻ.
| ÷ | |
|---|---|
|
Division sign |
|
| In Unicode | U+00F7 ÷ DIVISION SIGN (÷, ÷) |
| Different from | |
| Different from | U+2052 ⁒ COMMERCIAL MINUS SIGN U+002B + PLUS SIGN U+2020 † DAGGER U+034B ͋ COMBINING HOMOTHETIC ABOVE |
| Related | |
| See also | U+00D7 × MULTIPLICATION SIGN |
The division sign (÷) is a symbol consisting of a short horizontal line with a dot above and another dot below, used in Anglophone countries to indicate mathematical division. However, this usage, though widespread in some countries, is not universal; it is used for other purposes in other countries and its use to denote division is not recommended in the ISO 80000-2 standard for mathematical notation.[1]
In mathematics[edit]
The symbol does not represent division in every country. Here it is being used as a minus sign (not as a division sign) in an excerpt from an official Norwegian trading statement form called «Næringsoppgave 1» for the taxation year 2010.
The obelus, a historical glyph consisting of a horizontal line with (or without) one or more dots, was first used as a symbol for division in 1659, in the algebra book Teutsche Algebra by Johann Rahn, although previous writers had used the same symbol for subtraction.[2] Some near-contemporaries believed that John Pell, who edited the book, may have been responsible for this use of the symbol.[2] Other symbols for division include the slash or solidus /, the colon :, and the fraction bar (the horizontal bar in a vertical fraction).[3][4] The ISO 80000-2 standard for mathematical notation recommends only the solidus / or «fraction bar» for division, or the «colon» : for ratios; it says that the ÷ sign «should not be used» for division.[1]
In Italy, Poland and Russia, the ÷ sign was sometimes used to denote a range of values, and in Scandinavian countries it was used as a negation sign.[5]
Historically, an oblique form of the obelus, ⁒ (commercial minus sign), has also been used to represent subtraction in Northern Europe; such usage continued in some parts of Europe, including Norway and—until fairly recently—Denmark.[citation needed]
In computer systems[edit]
Encoding[edit]
The symbol was assigned to code point 0xF7 in ISO 8859-1, as the «division sign». This encoding was transferred to Unicode as U+00F7.[6] In HTML, it can be encoded as ÷ or ÷ (at HTML level 3.2), or as ÷.
Keyboard entry[edit]
In Microsoft Windows, this division sign is produced with Alt+0247 (or 246 with no zero) on the number pad, or by pressing Alt Gr+⇧ Shift++ when an appropriate keyboard layout is in use. In classic Mac OS and macOS, it is produced with ⌥ Option+/.
On UNIX-based systems using Screen or X with a Compose key enabled, it can be produced by composing : (colon) and - (hyphen/minus). It may also be produced using its Unicode code-point (F7), by pressing Control+⇧ Shift+u f7space.
In LaTeX, the division sign is obtained by the command div.
In ChromeOS (with International/Extended keyboard setting), the division sign is obtained by pressing AltGr+⇧ Shift++. Otherwise, the Unix-style methods may be used.
See also[edit]
- Plus and minus signs
- Multiplication sign
Notes[edit]
- ^ a b ISO 80000-2, Section 9 «Operations», 2-9.6
- ^ a b Cajori, Florian (1928). A history of mathematical notations. Vol. 1. Notations in Elementary Mathematics. The Open Court Company. pp. 242, 270–271. pp 270,271
- ^ Weisstein, Eric W. «Division». mathworld.wolfram.com. Retrieved 2020-08-26.
- ^ «Division». www.mathsisfun.com. Retrieved 2020-08-26.
- ^ «6. Writing Systems and Punctuation». The Unicode® Standard: Version 10.0 – Core Specification (PDF). Unicode Consortium. June 2017. p. 280, Obelus.
- ^ Korpela, Jukka (2006), Unicode Explained: Internationalize documents, programs, and web sites, O’Reilly Media, Inc., p. 397, ISBN 9780596101213
External links[edit]
- Jeff Miller: Earliest Uses of Various Mathematical Symbols
- Michael Quinion: Where our arithmetic symbols come from
The dictionary definition of division sign at Wiktionary
«÷» redirects here. For the music album of this name, see ÷ (album). For the Tifinagh character, see ⴻ.
| ÷ | |
|---|---|
|
Division sign |
|
| In Unicode | U+00F7 ÷ DIVISION SIGN (÷, ÷) |
| Different from | |
| Different from | U+2052 ⁒ COMMERCIAL MINUS SIGN U+002B + PLUS SIGN U+2020 † DAGGER U+034B ͋ COMBINING HOMOTHETIC ABOVE |
| Related | |
| See also | U+00D7 × MULTIPLICATION SIGN |
The division sign (÷) is a symbol consisting of a short horizontal line with a dot above and another dot below, used in Anglophone countries to indicate mathematical division. However, this usage, though widespread in some countries, is not universal; it is used for other purposes in other countries and its use to denote division is not recommended in the ISO 80000-2 standard for mathematical notation.[1]
In mathematics[edit]
The symbol does not represent division in every country. Here it is being used as a minus sign (not as a division sign) in an excerpt from an official Norwegian trading statement form called «Næringsoppgave 1» for the taxation year 2010.
The obelus, a historical glyph consisting of a horizontal line with (or without) one or more dots, was first used as a symbol for division in 1659, in the algebra book Teutsche Algebra by Johann Rahn, although previous writers had used the same symbol for subtraction.[2] Some near-contemporaries believed that John Pell, who edited the book, may have been responsible for this use of the symbol.[2] Other symbols for division include the slash or solidus /, the colon :, and the fraction bar (the horizontal bar in a vertical fraction).[3][4] The ISO 80000-2 standard for mathematical notation recommends only the solidus / or «fraction bar» for division, or the «colon» : for ratios; it says that the ÷ sign «should not be used» for division.[1]
In Italy, Poland and Russia, the ÷ sign was sometimes used to denote a range of values, and in Scandinavian countries it was used as a negation sign.[5]
Historically, an oblique form of the obelus, ⁒ (commercial minus sign), has also been used to represent subtraction in Northern Europe; such usage continued in some parts of Europe, including Norway and—until fairly recently—Denmark.[citation needed]
In computer systems[edit]
Encoding[edit]
The symbol was assigned to code point 0xF7 in ISO 8859-1, as the «division sign». This encoding was transferred to Unicode as U+00F7.[6] In HTML, it can be encoded as ÷ or ÷ (at HTML level 3.2), or as ÷.
Keyboard entry[edit]
In Microsoft Windows, this division sign is produced with Alt+0247 (or 246 with no zero) on the number pad, or by pressing Alt Gr+⇧ Shift++ when an appropriate keyboard layout is in use. In classic Mac OS and macOS, it is produced with ⌥ Option+/.
On UNIX-based systems using Screen or X with a Compose key enabled, it can be produced by composing : (colon) and - (hyphen/minus). It may also be produced using its Unicode code-point (F7), by pressing Control+⇧ Shift+u f7space.
In LaTeX, the division sign is obtained by the command div.
In ChromeOS (with International/Extended keyboard setting), the division sign is obtained by pressing AltGr+⇧ Shift++. Otherwise, the Unix-style methods may be used.
See also[edit]
- Plus and minus signs
- Multiplication sign
Notes[edit]
- ^ a b ISO 80000-2, Section 9 «Operations», 2-9.6
- ^ a b Cajori, Florian (1928). A history of mathematical notations. Vol. 1. Notations in Elementary Mathematics. The Open Court Company. pp. 242, 270–271. pp 270,271
- ^ Weisstein, Eric W. «Division». mathworld.wolfram.com. Retrieved 2020-08-26.
- ^ «Division». www.mathsisfun.com. Retrieved 2020-08-26.
- ^ «6. Writing Systems and Punctuation». The Unicode® Standard: Version 10.0 – Core Specification (PDF). Unicode Consortium. June 2017. p. 280, Obelus.
- ^ Korpela, Jukka (2006), Unicode Explained: Internationalize documents, programs, and web sites, O’Reilly Media, Inc., p. 397, ISBN 9780596101213
External links[edit]
- Jeff Miller: Earliest Uses of Various Mathematical Symbols
- Michael Quinion: Where our arithmetic symbols come from
The dictionary definition of division sign at Wiktionary
÷ Знак деления
Нажмите, чтобы скопировать и вставить символ
Значение символа
Знак деления. Дополнение к латинице — 1.
Символ «Знак деления» был утвержден как часть Юникода версии 1.1 в 1993 г.
Свойства
| Версия | 1.1 |
| Блок | Дополнение к латинице — 1 |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 00F7 |
| Простое изменение регистра | 00F7 |
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | C3 B7 | 195 183 | 50103 | 11000011 10110111 |
| UTF-16BE | 00 F7 | 0 247 | 247 | 00000000 11110111 |
| UTF-16LE | F7 00 | 247 0 | 63232 | 11110111 00000000 |
| UTF-32BE | 00 00 00 F7 | 0 0 0 247 | 247 | 00000000 00000000 00000000 11110111 |
| UTF-32LE | F7 00 00 00 | 247 0 0 0 | 4143972352 | 11110111 00000000 00000000 00000000 |
Знак разделить как пишется
Самый старый знак деления скорее всего знак ( / ) . Впервые его использовал английский математик Уильям Отред в своём труде Clavis Mathematicae (1631, Лондон).
Немецкий математик Лейбниц предпочитал двоеточие ( : ) . Этот символ он использовал впервые в 1684 году в своём труде Acta eruditorum. До Лейбница этот знак был использован англичанином Джонсоном в 1633 году в одной книге, но как знак дроби, а не деления в узком смысле.
Немецкий математик Йоханн Ран ввёл для обозначения деления знак ( ÷ ) . Вместе со знаком умножения в виде звёздочки ( ∗ ) он появился в его книге «Teutsche Algebra» в 1659 году. Из-за распространения в Англии знак Рана часто называют «английским знаком деления», но корни его лежат в Германии.
Другие употребления символов ( ÷ ) и ( : )
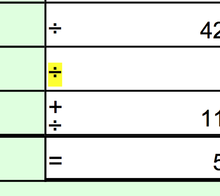
Символы ( ÷ ) и ( : ) могут использоваться также для обозначения диапазона. Например, «5÷10» может обозначать диапазон [5, 10], то есть от 5 до 10 включительно. Если имеется таблица, строки которой обозначаются числами, а столбцы — латинскими буквами, то запись вида «D4:F11» может использоваться для обозначения массива ячеек (двумерного диапазона) от D до F и от 4 до 11.
Источник статьи: http://dic.academic.ru/dic.nsf/ruwiki/232402
Блог молодого админа
Увлекательный блог увлеченного айтишника
Знак деления на клавиатуре компьютера или ноутбука: как поставить?
Если вы печатаете с помощью клавиатуры своего компьютера или ноутбука математические примеры, то можете все символы набрать на самой клавиатуре. Не верите? В этой статье мы покажем пример со знаком деления. Способов будет несколько. Какой из них использовать, решать вам. Начнем с наиболее простого.
Двоеточие
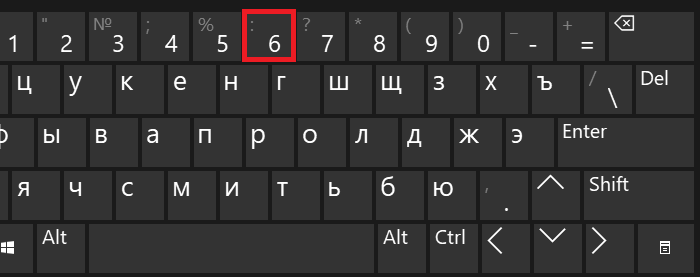
Надо отметить, что знаком деления могут выступать различные символы. Один из них — это двоеточие, находится он на той же клавише, что и цифра 6.
Чтобы поставить этот знак, нужно нажать на Shift и, удерживая клавишу, нажать на клавишу 6, после чего отпустить Shift.
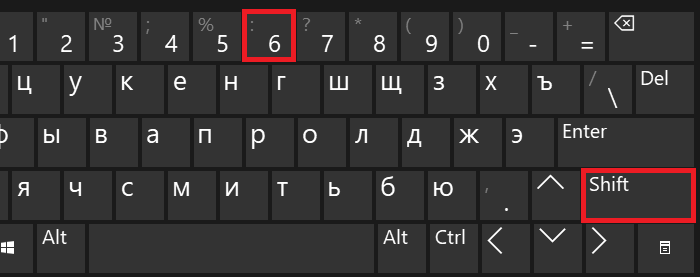
Если вы вдруг увидели другой символ, это говорит о том, что у вас используется англоязычная раскладка. Переключите ее на русскоязычную, нажав на клавиши Shift+Ctrl:
Можете также воспользоваться Alt-кодом. Для этого зажмите Alt и, удерживая его, наберите цифры 58, после чего отпустите Alt.
Если все сделано верно, вы увидите двоеточие.
Если не получилось с правым Alt, используйте левый.
Косая черта
В качестве знака деления может выступать косая черта. Она находится рядом с цифровой клавиатурой.
Просто нажмите на нее один раз.
Что должно получиться:
Раскладка клавиатуры роли не играет.
Alt-код для косой черты — 47:
Символ умножения из таблицы символов
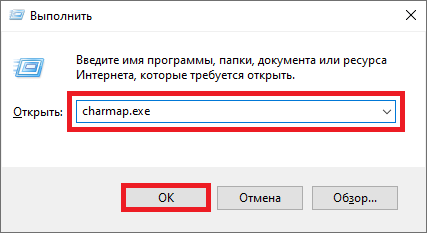
Можете использовать таблицу символов Windows, чтобы указать обелюс (знак деления), который обычно встречается на калькуляторах.
Затем в окно «Выполнить» введите команду charmap.exe и кликните ОК.
Если все сделали верно, увидите таблицу символов Windows.
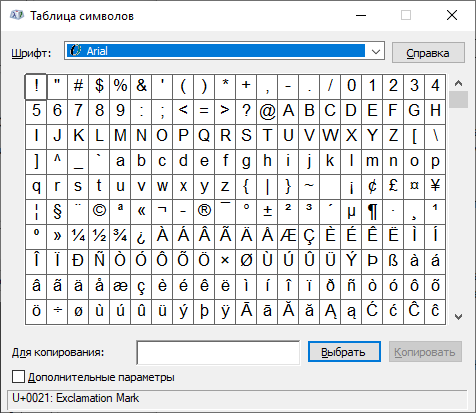
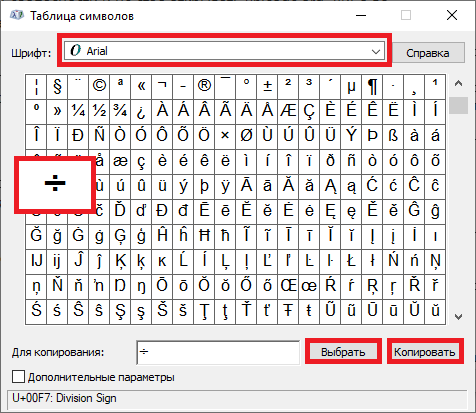
Выбираете шрифт Arial, находите символ деления, кликаете по нему, после чего кликаете по кнопкам «Выбрать» и «Копировать».
Можно использовать и Alt-коды.
В данном случае нужно набрать цифры 0247 на цифровой клавиатуре (англоязычная раскладка).
Источник статьи: http://fulltienich.com/znak-deleniya-na-klaviature-kompyutera-ili-noutbuka-windows/
Знак деления
Знак деления — математический символ в виде двоеточия ( : ) , обелюса ( ÷ ) или косой черты ( / ) , используемый для обозначения оператора деления.
В большинстве стран предпочитают двоеточие ( : ) , в англоязычных странах и на клавишах микрокалькуляторов — символ ( ÷ ) . Для математических формул во всём мире отдают предпочтение знаку ( / ) .
История символа
Самый старый знак деления скорее всего знак ( / ) . Впервые его использовал английский математик Уильям Отред в своём труде Clavis Mathematicae (1631, Лондон).
Немецкий математик Лейбниц предпочитал двоеточие ( : ) . Этот символ он использовал впервые в 1684 г. в своём труде Acta eruditorum. До Лейбница этот знак был использован англичанином Джонсоном 1633 в одной книге, но как знак дроби, а не деления в узком смысле.
Немецкий математик Йоханн Ран ввёл для обозначения деления знак ( ÷ ) . Вместе со знаком умножения в виде звездочки ( ∗ ) он появился в его книге «Teutsche Algebra» 1659 г. Из-за распространения в Англии знак Рана часто называют «английским знаком деления», но корни его лежат в Германии.
Другие употребления символов ( ÷ ) и ( : )
Символы ( ÷ ) и ( : ) могут использоваться также для обзначения диапазона. Например, «5÷10» может обозначать диапазон [5, 10], то есть от 5 до 10 включительно. Если имеется таблица, строки которой обозначаются числами, а столбцы — латинскими буквами, то запись вида «D4:F11» может использоваться для обозначения массива ячеек (двумерного диапазона) от D до F и от 4 до 11.
Источник статьи: http://vlab.wikia.org/ru/wiki/%D0%97%D0%BD%D0%B0%D0%BA_%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F
Как называется знак решётки? &, #, ÷, *
“Знак решётки”, “деление”, “вместо and”, “звёздочка” , “буква R”, “вопрос наоборот” – как правильно называются символы?
ДЕЛЕНИЕ – “ОБЕЛЮС”
От латинского obelus — от греческого ὀβελός. В этих словах тот же корень, что и в слове обелиск.
Именно так – обелюс – называется знак деления. Он напоминает объединение знаков минуса и двоеточия. Был введён древнегреческим филологом, александрийским библиотекарем Зенодотом Эфесским для обозначения сомнительности. Символ мог выглядеть либо как обычная горизонтальная черта, либо как та же черта, но с добавлением точек по одной сверху и снизу. Ставился на полях напротив тех частей текста, которые вызывали сомнения в ходе проверки поступавших в библиотеку рукописей.
В 1659 году немецкий математик Йоханн Ран в своей работе впервые применил обелюс для обозначения деления. Некоторые авторы использовали этот символ как знак вычитания, что стало нормой в некоторых странах Европы – например в Норвегии и Дании. В Польше обелюс использовался для обозначения диапазонов, например, запись 3÷7 означала «от трёх до семи».
РЕШЁТКА – ОКТОТОРП
От латинского octothorpe — восемь концов
Другие названия знака решётки – хеш, решётка, знак номера, диез или шарп (из-за внешнего сходства этих двух символов), знак фунта ( # часто используют в случаях, когда невозможно ввести символ фунта).
В 60-х годах XX века американские инженеры в области телефонии пытались придумать специальное название для этого символа, такие как октоторп, октаторп и октатерп. Однако ни одно из них так и не получило серьёзного распространения: все употребляли устоявшиеся формы hash sign (хеш-знак) или number sign (знак номера, который часто употребляют в английском языке).
Данный символ не был распространён в русской типографике вплоть до конца XX века. Неспециализированное, бытовое распространение знак получил с распространением цифрового набора номеров в телефонах. В языке за ним закрепился термин «знак решётки».
Источник статьи: http://zen.yandex.ru/media/tolk_slov/kak-nazyvaetsia-znak-reshetki—–5aa95947610493d45934e7c0
Деление в стоблик
Существуют элементарные вещи, не требующие объяснения. Но даже элементарное забывается, поэтому сегодня мы будем вспоминать деление в столбик.
Для примера разделим число 984 на 8. В любой операции деления есть делимое, делитель и частное. В нашем случае 984 – делимое, 8 – делитель, а результат деления – частное. Итак, будем искать частное от деления 984 на 8. Записываем рядом делимое и делитель, разделяя их уголком.
Теперь, двигаясь слева направо по цифрам делимого, найти в нем наименьшее число, которое больше делителя. Чисел тут три: 9, 98 и 984. Все они больше делителя (8), но наименьшим является 9. Теперь нужно ответить на вопрос: сколько раз наш делитель (8) содержится в числе 9? Один раз. Поэтому под чертой пишем 1– это первая цифра частного, которое мы пытаемся найти.

Теперь умножаем 8 на 1 и получаем 8. Записываем полученный результат под первым числом делимого. Далее вычитаем в столбик, то есть из 9 вычитаем 8 и получаем 1.

Если вы все сделали правильно, результат вычитания должен быть меньше делителя. У нас 1 меньше 8! Если у вас получилось больше, значит вы неправильно определили, сколько раз 8 содержится в 9.
Переходим к следующему этапу деления, для этого нужно увеличить наш результат вычитания. Делают это с помощью следующей цифры делимого. Первую цифру (9) мы уже использовали, значит, берем следующую (8) и приписываем к единице.

И снова отвечаем на знакомый вопрос. Сколько раз 8 содержится в 18? Два раза. Приписываем двойку к единице под чертой — это вторая цифра частного. Умножаем 2 на 8, получаем 16 и записываем результат под 18.

Дальше идем по уже знакомому пути. Вычитаем 16 из 18, получаем 2 (2 меньше 8, значит все сделано правильно). Используем следующую и последнюю цифру делимого – 4, сносим ее вниз и приписываем к двойке, получая 24.

Снова отвечаем на знакомый вопрос. Сколько раз 8 содержится в 24? Три раза. Пишем тройку под чертой. Умножаем 8 на 3, получаем 24 и записываем в столбик под 24. Вычитаем 24 из 24, получаем 0. Деление выполнено без остатка! Ответ – 123.

Если вы использовали все цифры делимого, а ноль так и не получился, значит или деление без остатка невозможно, или вы ошиблись в вычислениях.
Здесь вроде все просто, а как быть в случае, если при ответе на вопрос «Сколько раз делитель содержится в числе?» ответ – нисколько? Рассмотрим второй пример: теперь разделим 808 на 8: результат первого же вычитания равен нулю и приписываем к нулю тоже нуль. В этом случае в ноле восемь не содержится ни разу или нуль раз, значит записываем в результат нуль и сносим следующую цифру 8, а дальше повторяем знакомый алгоритм:

Все рассмотренные выше примеры заканчивались делением нацело, а как быть, если деление без остатка не возможно? В этом случае, когда цифры делимого закончились, в частном ставят десятичную запятую и приписывают к остатку от вычитания нули, продолжая известные действия деления в столбик. Например, при делении числа 804 на 8 приходим к случаю, когда в остатке вычитания нуль и приписанная цифра нуль – в результате записываем нуль и приписываем следующую цифру делимого (4), в которой 8 тоже содержится нуль раз. Снова в результат записываем нуль и ставим десятичную запятую, так как цифры делимого закончились, а приписываем 0. Теперь нужно определить сколько раз 8 содержится в 40. Пять раз. Продолжая деление в столбик, получаем в результате вычитания 0. Деление окончено.

И последний момент – это деление десятичных дробей. Для того, чтобы использовать приведенный алгоритм для деления десятичных дробей, необходимо умножить каждую из них на число 10 в степени, равной наибольшему количеству десятичных знаков после запятой в этих дробях. Например, нужно разделить 2025,255 на 2,5. Наибольшее количество знаков после запятой в делимом и оно равно 3. Значит умножить оба этих числа нужно на 10 в 3 степени, т. е. на 1000. Поэтому в столбик будем делить 2025255 на 2500. А это мы уже умеем.
Источник статьи: http://www.stranamam.ru/post/2531690/
Знак деления
-
Знак деления — математический символ в виде двоеточия (∶), обелюса (÷) или косой черты (∕), используемый для обозначения оператора деления.
В большинстве стран используют двоеточие (∶), в англоязычных странах и на клавишах микрокалькуляторов — символ (÷). В связи с большими неудобствами и даже невозможностью введения полноценных дробей в компьютер во времена операционных систем без GUI использовали упрощенные знаки для формул, в т.ч. для знака деления — использовали значок косой черты (⁄).
Источник: Википедия
Связанные понятия
О́белюс, обел (÷) (лат. obelus — от греч. ὀβελός, тот же корень, что и обелиск) — небуквенный символ, внешне напоминающий объединение знаков минуса и двоеточия.
Надстрочный знак, ве́рхний и́ндекс, суперскри́пт (англ. super script) (типографика) — знак, записанный выше основной строки. Применяется, например, при записи математических и химических формул.
Подробнее: Верхний индекс
Знаки «плюс» и «минус» (+ и −) — математические символы, используемые для обозначения операций сложения и вычитания, а также положительных и отрицательных величин. Кроме того, они используются и для обозначения других понятий. Латинские термины plus и minus означают «более» и «менее» соответственно.
Машинопи́сный апостро́ф (apostrophe, apostrophe-quote) — условное название знака, встречающегося на клавиатуре большинства пишущих машин с латинским шрифтом и компьютерных дисплеев. По историческим причинам лишь машинописный апостроф имеется на компьютерных клавиатурах и в 7-битовой кодировке ASCII. В качестве типографского символа он является суррогатом апострофа, кавычек, знака ударения, штриха (знака производной в математике, знака угловых минут и т. п.) и др. Часто смешивается с машинописным…
Веду́щие нули́ в записи числа при помощи позиционной системы счисления — последовательность из одного или более нулей, занимающая старшие разряды. Понятие ведущих нулей возникает при использовании представлений чисел, имеющих фиксированное количество разрядов. В остальных случаях, как правило, ведущие нули не пишутся.
Неразры́вный пробе́л (англ. non-breaking space) — элемент компьютерной кодировки текстов, отображающийся внутри строки подобно обычному пробелу, но не позволяющий программам отображения и печати разорвать в этом месте строку. Используется для автоматизации вёрстки, правила которой предписывают избегать разрыва строк в известных случаях (большей частью для удобочитаемости).
Перенос и заём в арифметике — приёмы, применяемые в арифметических алгоритмах позиционных систем счисления при выполнении операций сложения и вычитания соответственно, а также (в составе тех же сложения и вычитания) и иных арифметичких операций. Перенос можно понимать как выделение умножения на основание системы счисления в отдельное слагаемое, с последующей перегруппировкой слагаемых.
Универсальная тригонометрическая подстановка, в англоязычной литературе называемая в честь Карла Вейерштрасса подстановкой Вейерштрасса, применяется в интегрировании для нахождения первообразных, определённых и неопределённых интегралов от рациональных функций от тригонометрических функций. Без потери общности можно считать в данном случае такие функции рациональными функциями от синуса и косинуса. Подстановка использует тангенс половинного угла.
Рекурсивное определение или индуктивное определение определяет сущность в терминах её самой (то есть рекурсивно), хотя и полезным способом. Для того, чтобы это было возможно, определение в любом данном случае должно быть хорошо-основанным, избегая бесконечной регрессии.
Знак равенства (=) в математике, в логике и других точных науках — символ, который пишется между двумя идентичными по своему значению выражениями.
В математике, норма́льная фо́рма — простейший либо канонический вид, к которому объект приводится эквивалентными преобразованиями.
Нумерация Гёделя — это функция g, сопоставляющая каждому объекту некоторого формального языка её номер. С её помощью можно явно пронумеровать следующие объекты языка: переменные, предметные константы, функциональные символы, предикатные символы и формулы, построенные из них. Построение нумерации Гёделя для объектов теории называется арифметизацией теории — оно позволяет переводить высказывания, аксиомы, теоремы, теории в объекты арифметики. При этом требуется, чтобы нумерация g была эффективно вычислимой…
Математические обозначения («язык математики») — сложная графическая система обозначений, служащая для изложения абстрактных математических идей и суждений в человеко-читаемой форме. Составляет (по своей сложности и разнообразию) значительную долю неречевых знаковых систем, применяемых человечеством. В данной статье описывается общепринятая международная система обозначений, хотя различные культуры прошлого имели свои собственные, и некоторые из них даже имеют ограниченное применение до сих пор…
Греческая система счисления, также известная как ионийская или новогреческая — непозиционная система счисления. Алфавитная запись чисел, в которой в качестве символов для счёта, употребляют буквы классического греческого алфавита, а также некоторые буквы доклассической эпохи, такие как ϝ (дигамма), ϟ (коппа) и ϡ (сампи). Одно из начертаний дигаммы внешне похоже на распространившуюся в византийскую эпоху лигатуру ϛ (ϲτ), поэтому распространилось заблуждение, что для записи числа 6 использовалась стигма.Эта…
Календарная дата — порядковый номер календарного дня, порядковый номер или наименование календарного месяца и порядковый номер календарного года (Федеральный закон Российской Федерации от 3 июня 2011 г. № 107-ФЗ «Об исчислении времени»).
Минускульные цифры (старостильные цифры, «строчные» цифры) — символы арабских цифр, по высоте близкие к строчным буквам и обладающие (кроме цифр 0, 1 и 2) верхними или нижними выносными элементами. Предназначены для использования вместе со строчными буквами в тексте для сплошного чтения.
Дифференциа́л (от лат. differentia — разность, различие) в математике — линейная часть приращения дифференцируемой функции или отображения.
Армянская система счисления — историческая система счисления, созданная с использованием маюскулов (заглавных букв) армянского алфавита.
Тео́рия поле́й — раздел математики, занимающийся изучением свойств полей, то есть структур, обобщающих свойства сложения, вычитания, умножения и деления чисел.
Перебор делителей (пробное деление) — алгоритм факторизации или тестирования простоты числа путём полного перебора всех возможных потенциальных делителей.
При́знак Паска́ля — математический метод, позволяющий получить признаки делимости на любое число. Своего рода «универсальный признак делимости».
Геометрическая алгебра — историческое построение алгебры во второй книге «Начал» Евкида, где операции определялись непосредственно для геометрических величин, а теоремы доказывались геометрическими построениями.
Признаковое описание объекта (англ. feature vector) — это вектор, который составлен из значений, соответствующих некоторому набору признаков для данного объекта. Значения признаков могут быть различного, не обязательно числового, типа. Является одним из самых распространённых в машинном обучении способов ввода данных.
Языком Дика (англ. Dyck language) над 2n буквами называется контекстно-свободный язык над алфавитом…
Синглетон — множество с единственным элементом. Например, множество {0} является синглетоном.
Деление на ноль в математике — деление, при котором делитель равен нулю. Такое деление может быть формально записано а⁄0, где а — это делимое.
В теории чисел квадратным треугольным числом (или треугольным квадратным числом) называется число, являющееся как треугольным, так и квадратным.
Подробнее: Квадратное треугольное число
Гиппокра́товы лу́ночки — серповидные фигуры, указанные Гиппократом Хиосским, ограниченные дугами двух окружностей.
В теории представлений групп Ли и алгебр Ли, фундаментальное представление — это неприводимое конечномерное представление полупростой группы Ли или алгебры Ли, старший вес которого является фундаментальным весом. Например, определяющий модуль классической группы Ли является фундаментальным представлением. Любое конечномерное неприводимое представление полупростой группы Ли или алгебры Ли полностью определяется своим старшим весом (теорема Картана) и может быть построено из фундаментальных представлений…
Подробнее: Фундаментальное представление
Функция принадлежности нечёткого множества — обобщение индикаторной (или характеристической) функции классического множества. В нечёткой логике она представляет степень принадлежности каждого члена пространства рассуждения к данному нечёткому множеству.
Десятичный разделитель — знак, используемый для разделения целой и дробной частей вещественного числа в форме десятичной дроби в системе десятичного счисления. Для дробей в иных системах счисления может использоваться термин разделитель целой и дробной частей числа. Иногда также могут употребляться термины десятичная точка и десятичная запятая.
Теоре́ма Тоне́лли — Фуби́ни в математическом анализе, теории вероятностей и смежных дисциплинах сводит вычисление двойного интеграла к повторным.
Направленное множество в математике — непустое множество A с заданным на нем рефлексивным транзитивным отношением ≤ (то есть предпорядком), обладающее дополнительным свойством: у любой пары элементов из A есть верхняя грань в A.
Группа Григорчука — первый пример конечнопорождённой группы промежуточного роста (то есть её рост быстрее полиномиального, но медленнее экспоненциального).
Равноме́рная непреры́вность в математическом и функциональном анализе — это свойство функции быть одинаково непрерывной во всех точках области определения.
Ма́ркер списка, бу́ллит, бу́ллет, бу́лит (•) (англ. bullet) — типографский знак, используемый для выделения элементов списка, как показано на примере ниже…
Преобразование в математике — отображение (функция) множества в себя. Иногда (в особенности в математическом анализе и геометрии) преобразованиями называют отображения, переводящие некоторое множество в другое множество.
Единичный отрезок — величина, принимаемая за единицу при геометрических построениях. При изображении декартовой системы координат, единичный отрезок обычно отмечается на каждой из осей.
Звёздочка, или астери́ск (греч. ἀστέρισκος) — типографский знак в виде небольшой, обычно пяти- или шестиконечной звёздочки (*), расположенной в строке или поднятой над строкой.
Полурешётка (англ. semilattice, до 1960-х годов также использовался термин полуструктура) в общей алгебре — полугруппа, бинарная операция в которой коммутативна и идемпотентна.
Группы сферической симметрии также называются точечными группами в трёхмерном пространстве, однако эта статья рассматривает только конечные симметрии.
Φ, φ (название: фи, греч. φι) — 21-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 500. От буквы «фи» произошла кириллическая буква Ф.
Дискре́тное простра́нство в общей топологии и смежных областях математики — это пространство, все точки которого изолированы друг от друга в некотором смысле.
Список обозначений в физике включает обозначения понятий в физике из школьного и университетского курсов. Также включены и общие математические понятия и операции для того, чтобы сделать возможным полное прочтение физических формул.
Моноидальная категория (или тензорная категория) — категория C, снабженная бифунктором…
Квазиньютоновские методы — методы оптимизации, основанные на накоплении информации о кривизне целевой функции по наблюдениям за изменением градиента, чем принципиально отличаются от ньютоновских методов. Класс квазиньютоновских методов исключает явное формирование матрицы Гессе, заменяя её некоторым приближением.
|
÷ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Знак деления | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
:
÷
/
Знак деления — математический символ в виде двоеточия (:), обелюса (÷) или косой черты (/), используемый для обозначения оператора деления.
В большинстве стран предпочитают двоеточие (:), в англоязычных странах и на клавишах микрокалькуляторов — символ (÷). Для математических формул во всём мире отдают предпочтение знаку (/).
История символа
Самый старый знак деления скорее всего знак (/). Впервые его использовал английский математик Уильям Отред в своём труде Clavis Mathematicae (1631, Лондон).
Немецкий математик Лейбниц предпочитал двоеточие (:). Этот символ он использовал впервые в 1684 году в своём труде Acta eruditorum. До Лейбница этот знак был использован англичанином Джонсоном в 1633 году в одной книге, но как знак дроби, а не деления в узком смысле.
Немецкий математик Йоханн Ран ввёл для обозначения деления знак (÷). Вместе со знаком умножения в виде звёздочки (∗) он появился в его книге «Teutsche Algebra» в 1659 году. Из-за распространения в Англии знак Рана часто называют «английским знаком деления», но корни его лежат в Германии.
Другие употребления символов (÷) и (:)
Символы (÷) и (:) могут использоваться также для обозначения диапазона. Например, «5÷10» может обозначать диапазон [5, 10], то есть от 5 до 10 включительно. Если имеется таблица, строки которой обозначаются числами, а столбцы — латинскими буквами, то запись вида «D4:F11» может использоваться для обозначения массива ячеек (двумерного диапазона) от D до F и от 4 до 11.
Кодировка
| Знак | Unicode | Название | HTML/XML | LaTeX | |||
|---|---|---|---|---|---|---|---|
| код | название | шестнадцатерично | десятично | названно | |||
| (:) | U+003A | Colon | двоеточие | : | : | отсутствует | : |
| (÷) | U+00F7 | Division sign | ÷ | ÷ | ÷ | div | |
| (∕) | U+2215 | Division slash | ∕ | ∕ | отсутствует | / | |
| (⁄) | U+2044 | Fraction slash | знак дроби | ⁄ | ⁄ | ⁄ | / |
Литература
- Florian Cajori: A History of Mathematical Notations. Dover Publications 1993
См. также
Дробь (математика)
| |
|---|
| Плюс ( + ) • Минус ( − ) • Знак умножения ( · или × ) • Знак деления ( : или / ) • Знак корня ( √ ) • Знак равенства ( =, ≈, ≡ и др.) • Знаки неравенства ( ≠, >, < и др.) • Бесконечность ( ∞ ) • Знак интеграла ( ∫ ) • Факториал ( ! ) • Вертикальная черта ( | ) • Знак градуса ( ° ) • Минута градуса ( ′ ) • Секунда градуса ( ″ ) • Штрих ( ′ ) • Звёздочка ( * ) • Обратная косая черта, бэкслеш ( ) • Процент ( % ) • Промилле ( ‰ ) • Тильда ( ~ ) • Циркумфлекс ( ^ ) • Плюс-минус ( ± ) • Обелюс ( ÷ ) • Десятичный разделитель ( , или . ) |
| Математика • История математических обозначений |