Символьные обозначенияДля обозначения геометрических фигур и их проекций, для отображения отношения между геометрическими фигурами, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем используются символьные обозначения.
Символьные обозначения, все их многообразие, может быть подразделено на две группы: Символьные обозначения — Первая группа Символы, обозначающие геометрические фигуры и отношения между ними
Обозначения геометрических фигур:
O — точка пересечения осей проекций;
Проекции точек, линий, поверхностей любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса A`, A», A`» Символы взаиморасположения геометрических объектов
Символьные обозначения — Вторая группа Символы обозначающие логические операции
+ |
Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).
Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:
группа I — обозначения геометрических фигур и отношений между ними;
группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.
Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.
Группа I
СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ
А. Обозначение геометрических фигур
1. Геометрическая фигура обозначается — Ф.
2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:
А, В, С, D, … , L, М, N, …
1,2,3,4,…,12,13,14,…
3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:
а, b, с, d, … , l, m, n, …
Линии уровня обозначаются: h — горизонталь; f— фронталь.
Для прямых используются также следующие обозначения:
(АВ) — прямая, проходящая через точки А а В;
[АВ) — луч с началом в точке А;
[АВ] — отрезок прямой, ограниченный точками А и В.
4. Поверхности обозначаются строчными буквами греческого алфавита:
α, β, γ, δ,…,ζ,η,ν,…
Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:
α(а || b) — плоскость α определяется параллельными прямыми а и b;
β(d1 d2gα) — поверхность β определяется направляющими d1 и d2 , образующей g и плоскостью параллелизма α.
5. Углы обозначаются:
∠ABC — угол с вершиной в точке В, а также ∠α°, ∠β°, … , ∠φ°, …
6. Угловая: величина (градусная мера) обозначается знаком 


Прямой угол отмечается квадратом с точкой внутри
7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.
Например:
|АВ| — расстояние между точками А и В (длина отрезка АВ);
|Аа| — расстояние от точки А до линии a;
|Аα| — расстояшие от точки А до поверхности α;
|аb| — расстояние между линиями а и b;
|αβ| расстояние между поверхностями α и β.
8. Для плоскостей проекций приняты обозначения: π1 и π2,
где π1 — горизонтальная плоскость проекций;
π2 —фрюнтальная плоскость проекций.
При замене плоскостей проекций или введении новых плоскостей последние обозначают π3, π4 и т. д.
9. Оси проекций обозначаются: х, у, z, где х — ось абсцисс; у — ось ординат; z — ось аппликат.
Постояшную прямую эпюра Монжа обозначают k.
10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:
А’, В’, С’, D’, … , L’, М’, N’, горизонтальные проекции точек; А», В», С», D», … , L», М», N», … фронтальные проекции точек; a’ , b’ , c’ , d’ , … , l’, m’ , n’ , —
горизонтальные проекции линий; а» ,b» , с» , d» , … , l» , m» , n» , … фронтальные проекции линий; α’, β’, γ’, δ’,…,ζ’,η’,ν’,… горизонтальные проекции поверхностей;
α», β», γ», δ»,…,ζ»,η»,ν»,…
фронтальные проекции поверхностей.
11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса 0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.
Так: h0α — горизонтальный след плоскости (поверхности) α;
f0α — фронтальный след плоскости (поверхности) α.
12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.
Например: Ha — горизонтальный след прямой (линии) а;
Fa — фронтальный след прямой (линии ) a.
13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами 1,2,3,…, n:
А1, А2, А3,…,Аn;
a1, a2, a3,…,an;
α1, α2, α3,…,αn;
Ф1, Ф2, Ф3,…,Фn и т. д.
Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом 0:
A0, B0, С0, D0, …
Аксонометрические проекции
14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0:
А0, В0, С0, D0, …
10, 20, 30, 40, …
a0, b0, c0, d0, …
α0, β0, γ0, δ0, …
15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :
А1 0, В1 0, С1 0, D1 0, …
11 0, 21 0, 31 0, 41 0, …
a1 0, b1 0, c1 0, d1 0, …
α1 0, β1 0, γ1 0, δ1 0, …
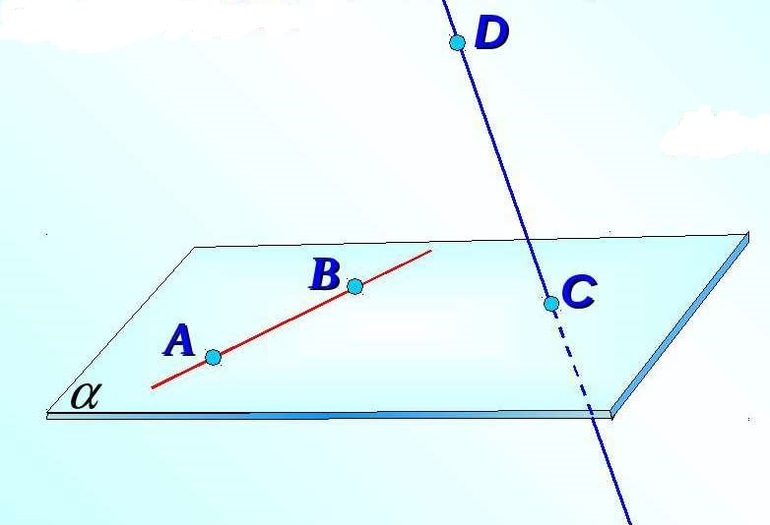
Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.
| № по пор. | Обозначение | Содержание | Пример символической записи |
|---|---|---|---|
| 1 | ≡ | Совпадают | (АВ)≡(CD) — прямая, проходящая через точки А и В, совпадает с прямой, проходящей через точки С и D |
| 2 | ≅ | Конгруентны | ∠ABC≅∠MNK — угол АВС конгруентен углу MNK |
| 3 | ∼ | Подобны | ΔАВС∼ΔMNK — треугольники АВС и MNK подобны |
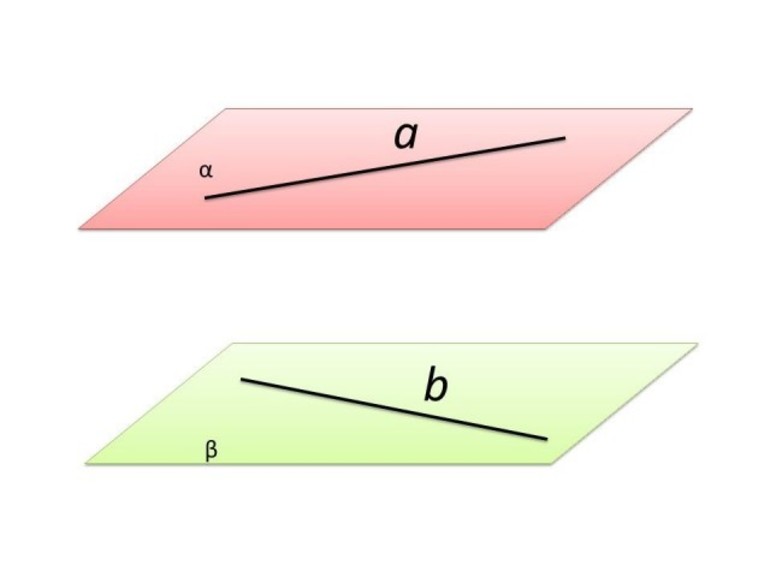
| 4 | || | Параллельны | α||β — плоскость α параллельна плоскости β |
| 5 | ⊥ | Перпендикулярны | а⊥b — прямые а и b перпендикулярны |
| 6 |  |
Скрещиваются | с  d — прямые с и d скрещиваются d — прямые с и d скрещиваются |
| 7 |  |
Касательные | t  l — прямая t является касательной к линии l. l — прямая t является касательной к линии l. β  α — плоскость β касательная к поверхности α α — плоскость β касательная к поверхности α |
| 8 | → | Отображаются | Ф1→Ф2 — фигура Ф1 отображается на фигуру Ф2 |
| 9 | S | Центр проецирования. Если центр проецирования несобственная точка, то его положение обозначается стрелкой, указывающей направление проецирования |
— |
| 10 | s | Направление проецирования | — |
| 11 | P | Параллельное проецирование | рsα Параллельное проецирование — параллельное проецирование на плоскость α в направлении s |
| № по пор. | Обозначение | Содержание | Пример символической записи | Пример символической записи в геометрии |
|---|---|---|---|---|
| 1 | M,N | Множества | — | — |
| 2 | A,B,C,… | Элементы множества |
— | — |
| 3 | { … } | Состоит из … | Ф{A, B, C,… } | Ф{A, B, C,… } — фигура Ф состоит из точек А, В,С, … |
| 4 | ∅ | Пустое множество | L — ∅ — множество L пустое (не содержит элементов ) | — |
| 5 | ∈ | Принадлежит, является элементом | 2∈N (где N — множество натуральных чисел) — число 2 принадлежит множеству N |
А ∈ а — точка А принадлежит прямой а (точка А лежит на прямой а ) |
| 6 | ⊂ | Включает, cодержит | N⊂М — множество N является частью (подмножеством) множества М всех рациональных чисел |
а⊂α — прямая а принадлежит плоскости α (понимается в смысле: множество точек прямой а является подмножеством точек плоскости α) |
| 7 | ∪ | Объединение | С = A U В — множество С есть объединение множеств A и В; {1, 2. 3, 4,5} = {1,2,3}∪{4,5} |
ABCD = [AB] ∪ [ВС] ∪ [CD] — ломаная линия, ABCD есть объединение отрезков [АВ], [ВС], [CD] |
| 8 | ∩ | Пересечение множеств | М=К∩L — множество М есть пересечение множеств К и L (содержит в себе элементы, принадлежащие как множеству К, так и множеству L). М ∩ N = ∅— пересечение множеств М и N есть пустое множество (множества М и N не имеют общих элементов) |
а = α ∩ β — прямая а есть пересечение плоскостей α и β а ∩ b = ∅ — прямые а и b не пересекаются (не имеют общих точек) |
| № по пор. | Обозначение | Содержание | Пример символической записи |
|---|---|---|---|
| 1 | ∧ | Конъюнкция предложений; соответствует союзу «и». Предложение (р∧q) истинно тогда и только тогда,когда р и q оба истинны |
α∩β = { К:K∈α∧K∈β} Пересечение поверхностей α и β есть множество точек (линия), состоящее из всех тех и только тех точек К, которые принадлежат как поверхности α, так и поверхности β |
| 2 | ∨ | Дизъюнкция предложений; соответствует союзу «или». Предложение (p∨q) истинно, когда истинно хотя бы одно из предложений р или q (т. е. или р, или q, или оба). |
— |
| 3 | ⇒ | Импликация — логическое следствие. Предложение р⇒q означает: «если р, то и q» | (а||с∧b||с)⇒a||b. Если две прямые параллельны третьей, то они параллельны между собой |
| 4 | ⇔ | Предложение (р⇔q) понимается в смысле: «если р, то и q; если q, то и р» | А∈α⇔А∈l⊂α. Точка принадлежит плоскости, если она принадлежит некоторой линии, принадлежащей этой плоскости. Справедливо также и обратное утверждение: если точка принадлежит некоторой линии, принадлежащей плоскости, то она принадлежит и самой плоскости |
| 5 | ∀ | Квантор общности, читается: для всякого, для всех, для любого. Выражение ∀(x)P(x) означает: «для всякого x: имеет место свойство Р(х) « |
∀( ΔАВС)(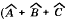 = 180°) Для всякого (для любого) треугольника сумма величин его углов = 180°) Для всякого (для любого) треугольника сумма величин его углов при вершинах равна 180° |
| 6 | ∃ | Квантор существования, читается: существует. Выражение ∃(х)P(х) означает: «существует х, обладающее свойством Р(х)» |
(∀α)(∃a)[a⊄α∧a||α].Для любой плоскости α существует прямая а, не принадлежащая плоскости α и параллельная плоскости α |
| 7 | ∃1 | Квантор единственности существования, читается: существует единственное (-я, -й)… Выражение ∃1(x)(Рх) означает: «существует единственное (только одно) х, обладающее свойством Рх» |
(∀ А, В)(А≠B)(∃1а)(а∋А, В) Для любых двух различных точек А и В существует единственная прямая a, проходящая через эти точки. |
| 8 | (Px) | Отрицание высказывания P(x) | а b(∃α)(α⊃а, Ь).Если прямые а и b скрещиваются, то не существует плоскости а, которая содержит их b(∃α)(α⊃а, Ь).Если прямые а и b скрещиваются, то не существует плоскости а, которая содержит их |
| 9 | Отрицание знака | [AB]≠[CD] —отрезок [АВ] не равен отрезку [CD].а?b — линия а не параллельна линии b |
Общая характеристика
Алгоритм определения того, что прямые линии (ПЛ) могут называться скрещивающимися, описывает расположение вне бесконечной поверхности. Существует несколько теорем и доказательств пересечения прямых в одной точке.
Основные понятия и теоремы
Из курса планиметрии известно, что две ПЛ в плоскости пересекаются, имеют одну точку или располагаются параллельно по отношению друг к другу.
Произвести вычисления, необходимые расчеты и графическое построение можно, изучив главные особенности и характеристику понятий. Когда прямые заданы векторными параметрическими уравнениями, выполняется равенство (формула) р = р0+SU и r = r0+tv.
Вычисление удаленности между ними определяется смешанным и векторным произведением D = (r 0 — p 0, u, v)/u, v.
Существует первая теорема, доказывающая признаки скрещивающихся ПЛ. Ее смысл заключается в теоретическом аспекте, указывающим на то, что когда одна из двух ПЛ расположена в плоскости, а другая ПЛ пересекает пространство в точке, не находящейся на отрезке, то эти ПЛ являются скрещивающимися. Данные можно доказать графически, используя методы черчения и рисования фигур, углов и перпендикуляров.
Например, дана плоскость α, в ней находится АВ, а прямая CD пересекается с плоскостью в т. С, расположенной на АВ. Для доказательства скрещивания прямых используется метод от обратного. Предполагается, что существует вторая плоскость, в которой расположены AB и DC. Во второй плоскости лежит отрезок АВ и т. С. Через ПЛ и точку, не лежащую на ней, проходит плоскость альфа. Второй плоскости бета не существует. Прямые скрещиваются.
Существует три положения прямых. В первом случае линии a и b пересекаются в т. С. Сквозь 2 ПЛ, которые пересекаются, проходит плоскость. ПЛ А II В, лежат в едином пространстве и не смогут пересечься. Прямые скрещиваются, когда не находятся в едином поле.
Вторая теорема о скрещивающихся прямых гласит, что через каждую из пары скрещивающихся ПЛ проходит одна плоскость, параллельная другой. Для подтверждения даны две ПЛ AB и CD. Требуется доказать, что через линию АВ проложена плоскость, параллельная СД.
Для этого через точку А проводится линия АЕ, расположенная параллельно DC. Согласно теореме о параллельных ПЛ, эта линия является единственной. Пересечение двух линий АВ и АЕ позволяет проложить плоскость альфа. Прямая DC, не лежащая в пространстве альфа, II АЕ, значит, DC параллельна пространству α.
Для доказательства единства такого пространства предполагается, что существует другая плоскость бета (β), проходящая через АВ, и является параллельной по отношению к DC.
Особенности ПЛ:
- Отрезок АЕ пересекает пространство бета, линия DC пересекает β.
- Отрезок DC не расположен параллельно бета.
Возникло противоречие, а плоскость α является единственной.
Прочие условия
У отрезков, которые скрещиваются, нет общей точки соприкосновения, потому что тогда они бы располагались в едином пространстве.
Признаки скрещивающихся прямых:
- Если на двух ПЛ имеются 4 точки, не находящиеся в одной плоскости, то линии будут скрещены. Если бы данные ПЛ были пересекающимися или параллельными по отношении друг к другу, то они лежали в единой плоскости.
- Чтобы сонаправить линии (сделать их параллельными по отношению друг к другу), угол между скрещивающимися прямыми должен быть 0 градусов. Величина, наименьшая из 2 пересекающихся линий, представляет собой угол. Когда все углы одинаковы, образуется его 90-градусный параметр и перпендикулярность.
Угол между скрещивающимися ПЛ — когда из одной точки выходят 2 луча между двумя ПЛ, которые пересекаются, а также параллельны данным линиям.
В тригонометрии еще существует понятие обозначения косинуса — это отношение длины стороны, прилежащей к острому углу, к гипотенузе. Осуществить нахождение ПЛ параллельно скрещивающимся можно через произвольную точку. Это официальное утверждение. Две ПЛ могут быть параллельными или пресекать плоскость, значит, они находятся в едином пространстве координат.
Практическое применение
Теоретические основы, понятия на уроках геометрии в режиме онлайн понятны, но для закрепления материала в классе решаются разные задачи с доказательствами. Сначала нужно найти в пространстве линии, углы и охарактеризовать их вид.
Типовые задачи
Чтобы на практике понять действие теорем, нужно использовать пример решения и наглядный рисунок. Например, точка D не лежит в плоскости АВС, точки M, N, P будут центром DA, DB и DC. Точка К расположена на прямой ВС. Требуется определить взаимное расположение линий.
1) ND, АВ.
Линии будут обозначаться буквами АВ и BD, они находятся в плоскости АВD и пересекаются.
2) PK и ВС.
Эти две линии расположены в единой плоскости, поэтому являются параллельными или пересекающимися. Нужно провести среднюю линию NP, где N, P являются серединой отрезка DB и DC. По свойству средней линии, NP II (знак параллельности) ВС. Через т. Р проводится отрезок, II ВС, и это NP. Любая другая линия, проходящая через т. Р, не II ВС, поэтому PK и ВС пересекаются.
3) MN и AB.
В треугольнике ABD точки M и N являются центрами сторон АD и ВD, значит, МN — средняя линия. Основываясь на типовых свойствах, МN II АВ.
4) МР и АС.
В ADС точки M и Р будут серединами АD и СD. Значит, МР является средней линией. МР IIАС.
5) КN и АС.
Прямопроходящая линия КN и ВD являются одной и той же прямой. АС располагается в плоскости АВС, линия ВD пересекает АВС в точке, не расположенной на АС. По признаку ВD и АС являются скрещивающимися, КN и АС — такая же.
6) МD и ВС.
MD и АD будут одинаковой ПЛ по всем характеристикам и параметрам. Линия ВС располагается в плоскости АВС, прямая АD пересекает АВС в точке, расположенной в стороне от ВС. АD и ВС относятся к скрещиванию, а МD и ВС такие же.
Сложные задания
В нижней части пирамиды SABC расположена геометрическая фигура с прямым углом при вершине С, гипотенузой АВ = 13 и катетом АС = 12 (когда 1 из 2 сторон прямоугольного треугольника образует прямой угол). Максимальная точка пирамиды S проектируется в основании В. Боковое ребро CS равняется 5*корень из 5. Требуется выяснить расстояние между ребрами AS и ВС.
Для решения нужно определить расстояние между отрезками AS и ВС. Они лежат на скрещивающихся прямых (СП). Точка s не принадлежит отрезку АВС, а точка А принадлежит АВС. AS пересекает АВС, ВС включает отрезок АВС и А не принадлежит ВС.
Расстояние между 1 из СП и плоскостью, проложенной через другую II первой, называется промежутком между СП. Нужно построить такое пространство, проходящее через 1 из СП, параллельно другой, и добавить перпендикуляр к пространству из точки, принадлежащей другой линии.
Выбрав прямую AS, нужно провести через нее плоскость, II ВС.
Пирамиду нужно достроить до параллелепипеда, через т. А на плоскости АВС проведя параллельную ВС и через т. В — АС. Точку пересечения ПЛ обозначают буквой D. Через А, С, D нужно провести прямые II SB, на каждой отложить отрезки, равные BS, а точки соединить линиями.
Определение скрещивающихся прямых подтверждено теоремами, также существует условие, описывающее, что через каждую пару ПЛ, которые скрещены, проложена плоскость, II другой линии. Изучены случаи расположения ПЛ в пространстве: они пересекаются, являются параллельными или скрещиваются.