Как пишется знак следовательно в геометрии

Определение и знак подобия в геометрии

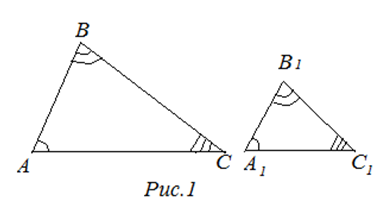
Обозначают подобие треугольников знаком «».

Пример. (читают: треугольник подобен треугольнику ).

Коэффициент подобия треугольников и знак подобия

Иногда над знаком подобия ставят коэффициент подобия треугольников, т.е. .

Знак «» представляет собой типографский знак «тильда», который изображается в виде волнистой черты. Этот знак может быть как надстрочным, так и междустрочным.

В математике «тильда» используется для обозначения различных видов отношений эквивалентности, в частности, отношения подобия.

Знак «тильда» (или «двойная тильда» ), который стоит перед числом может означать «примерно», «приблизительно равно».

В алгебре высказываний знак «» обозначает логическую операцию «эквиваленция».

Если знак «тильда» сочетать со знаком равенства: «», то он будет обозначать отношение конгруэнтности.

Также знак «тильда» активно используется в информатике и вычислительной технике. Например, в редакторе Tex этот знак означает «неразрывный пробел».

Понравился сайт? Расскажи друзьям!

Ольга Чернышева

Ученик

(122),
закрыт

7 лет назад

Ниже представлена таблица с основными математическими символами и знаками, которые используются в геометрии с 7 класса и старше.

Знак	Название	Значение/описание	Пример
∠	угол	фигура, состоящая из двух лучей и вершины	∠ABC = 30°
	острый угол	угол от 0 до 90 градусов	∠AOB = 60°
	прямой угол	угол, равный 90 граусам	∠AOB = 90°
	тупой угол	угол от 90 до 180 градусов	∠AOB = 120°
	развернутый угол	угол, равный 180 градусам	∠AOB = 180°
° (или deg)	градус	единица измерения угла, равна 1/360 окружности	45°
′	минута	единица измерения угла, 1° = 60′	α = 70°59′
″	секунда	единица измерения угла, 1′ = 60″	α = 70°59′59″
	линия	бесконечная прямая без начала и конца
	отрезок	участок на прямой между точками A и B
	луч	бесконечная прямая, имеющая начало в точке A, но не имеющая конца
	дуга	дуга, образованная между точками A и B
⊥	перпендикулярность	линии (прямые), расположенные под углом 90° по отношению друг к другу	AC ⊥ BC
||	параллельность	непересекающиеся прямые (линии)	AB || CD
∩	пересечение	множество одинаковых элементов, принадлежащих как множеству A, так и B	A ∩ B
∈ / ∉	принадлежность/ непринадлежность	элемент является/не является элементом заданного множества	a ∈ S
≅	конгуэнтность	эквивалентность геометрических форм и размеров	∆ABC ≅ ∆XYZ
~	подобие	та же форма, но разные размеры	∆ABC ~ ∆XYZ
Δ	треугольник	фигура треугольника	ΔABC ≅ ΔBCD
|x-y|	дистанция	дистанция между точками X и Y	| x-y | = 5
π	константа «Пи»	отношение длины окружности к диаметру круга, π = C/d	π = 3.141592654…
рад (rad) или c	радиан	единица измерения угла	360° = 2π c

microexcel.ru

Опубликовано — 2 года назад | По предмету
Геометрия |
автор julia2000B

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Сегодня 02.05.2022 07:56 свежие новости час назад
Прогноз на сегодня : Как пишется знак следовательно в геометрии . Развитие событий.

Актуально сегодня (02.05.2022 07:56): Как пишется знак следовательно в геометрии

Моменты силы относительно точки и оси в теоретической. Интеграл и его применение с примерами решения. ГАРАНТ Garant.В развитие интегрального исчисления значительный вклад внесли российские математики украинского происхождения М. В. Остроградский 1801 1862 В.Я.Буняковский 1804 1889 Вопрос: В организацию поступило дополнительное соглашение к договору поставки от 22.03.2022 от организации находящейся в РФ в котором говорится что цена товара поставляемого по договору также может устанавливаться в .

1. Как пишется знак следовательно в геометрии

2. Как выглядит знак следовательно в геометрии

3. Как пишется значок следовательно в геометрии

4. Как пишется знак принадлежит в геометрии

Как пишется знак следовательно в геометрии

Как пишется знак следовательно в геометрии

Как пишется знак следовательно в геометрии

Как пишется знак следовательно в геометрии

Как пишется знак следовательно в геометрии

Как пишется знак следовательно в геометрии

Как пишется знак следовательно в геометрии
Как пишется знак следовательно в геометрии
Как пишется знак следовательно в геометрии
Как пишется знак следовательно в геометрии
Как пишется знак следовательно в геометрии

Как пишется знак следовательно в геометрии

9041462618282665b80f0416d63c2cfc d6ccf4bfdafd7f9ce92d65f62548d457
Как пишется знак следовательно в геометрии
Как пишется знак следовательно в геометрии
Как пишется знак следовательно в геометрии

firmware prestigio through the computer | проект по формированию культурно-гигиенических навыков в подготовительной группе | firmware galaxy s | мария пирогова голое фото | решу впр 7 класс английский язык | Thomas fontana пылесос инструкция | проститутки ставрополья | the firmware upgrade motor to ffd 1 05 | edit firmware jan 5 1 | Призначення та тактико технічні характеристики пістолета форт |

Invision Community © 2022 IPS, Inc.
Карта сайт Rss
s
p

Морфемный разбор слова:

Однокоренные слова к слову:

Обозначения и символика

Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).

Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:

группа I — обозначения геометрических фигур и отношений между ними;

группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.

Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.

СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ

А. Обозначение геометрических фигур

1. Геометрическая фигура обозначается — Ф.

2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:

3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:

Линии уровня обозначаются: h — горизонталь; f— фронталь.

Для прямых используются также следующие обозначения:

(АВ) — прямая, проходящая через точки А а В;

[АВ) — луч с началом в точке А;

[АВ] — отрезок прямой, ограниченный точками А и В.

4. Поверхности обозначаются строчными буквами греческого алфавита:

Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:

α(а || b) — плоскость α определяется параллельными прямыми а и b;

5. Углы обозначаются:

6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:

— величина угла АВС;

— величина угла φ.

Прямой угол отмечается квадратом с точкой внутри

7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.

|АВ| — расстояние между точками А и В (длина отрезка АВ);

|Аа| — расстояние от точки А до линии a;

|Аα| — расстояшие от точки А до поверхности α;

|аb| — расстояние между линиями а и b;

|αβ| расстояние между поверхностями α и β.

π₂ —фрюнтальная плоскость проекций.

При замене плоскостей проекций или введении новых плоскостей последние обозначают π₃, π₄ и т. д.

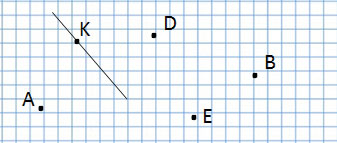
Постояшную прямую эпюра Монжа обозначают k.

10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:

11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса _0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.

12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.

Например: H_a — горизонтальный след прямой (линии) а;

F_a — фронтальный след прямой (линии ) a.

13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами _{1,2,3. n:}

Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом ₀:

14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0 :

15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :

Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.

Источник

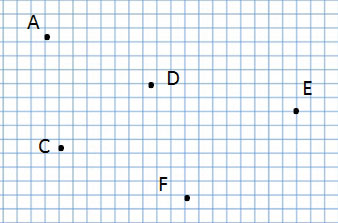
Обозначение геометрических фигур буквами

В математике есть правило: обозначать геометрические фигуры заглавными буквами латинского алфавита. Сегодня мы научимся этому.

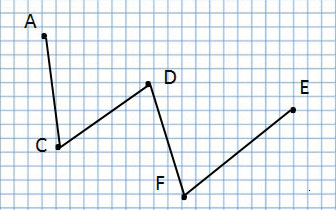
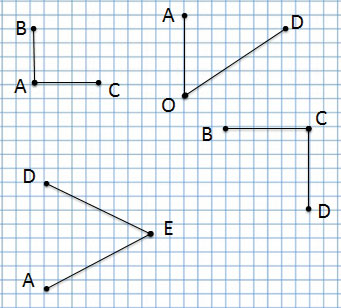
Точка

точка А, точка С, точка D, точка Е и точка F.

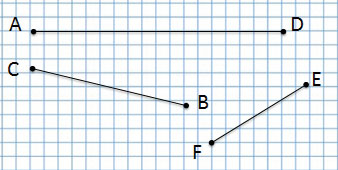
Отрезок

отрезок AD, отрезок СВ, отрезок FE

Сколько всего отрезков на данном чертеже?

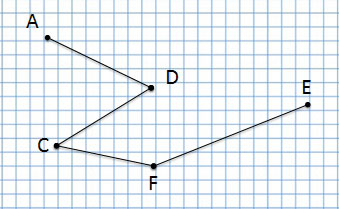
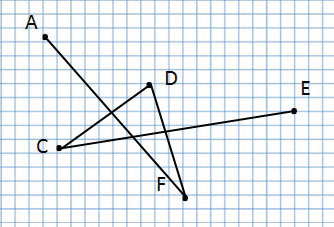
Ломаная линия

А эта ломаная линия совсем по-другому, потому что соединение точек у неё другое:

Ломаная линия ACDFE

Прочитаю название следующей ломаной линии:

Ломаная линия AFDCE

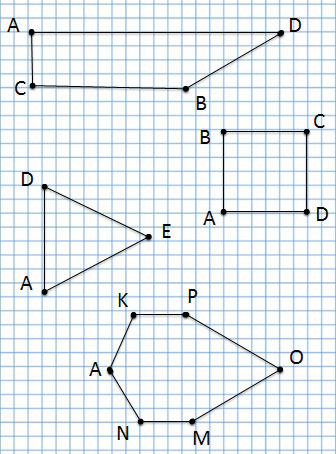
Многоугольники

Угол

Угол обозначается тремя буквами. В середине указывается буква, которая обозначает вершину угла.

1 угол: угол BAC или CAB с вершиной А

2 угол: угол AOD или DOA с вершиной О

3 угол: угол AED или DEA с вершиной Е

4 угол: угол BCD или DCB с вершиной С

Поделись с друзьями в социальных сетях:

Источник

Обозначение геометрических фигур буквами

В математике есть правило: обозначать геометрические фигуры заглавными буквами латинского алфавита. Сегодня мы научимся этому.

Точка

точка А, точка С, точка D, точка Е и точка F.

Отрезок

отрезок AD, отрезок СВ, отрезок FE

Сколько всего отрезков на данном чертеже?

Ломаная линия

А эта ломаная линия совсем по-другому, потому что соединение точек у неё другое:

Ломаная линия ACDFE

Прочитаю название следующей ломаной линии:

Ломаная линия AFDCE

Многоугольники

Угол

Угол обозначается тремя буквами. В середине указывается буква, которая обозначает вершину угла.

1 угол: угол BAC или CAB с вершиной А

2 угол: угол AOD или DOA с вершиной О

3 угол: угол AED или DEA с вершиной Е

4 угол: угол BCD или DCB с вершиной С

Поделись с друзьями в социальных сетях:

Источник

Обозначение геометрических фигур буквами

В математике есть правило: обозначать геометрические фигуры заглавными буквами латинского алфавита. Сегодня мы научимся этому.

Точка

точка А, точка С, точка D, точка Е и точка F.

Отрезок

отрезок AD, отрезок СВ, отрезок FE

Сколько всего отрезков на данном чертеже?

Ломаная линия

А эта ломаная линия совсем по-другому, потому что соединение точек у неё другое:

Ломаная линия ACDFE

Прочитаю название следующей ломаной линии:

Ломаная линия AFDCE

Многоугольники

Угол

Угол обозначается тремя буквами. В середине указывается буква, которая обозначает вершину угла.

1 угол: угол BAC или CAB с вершиной А

2 угол: угол AOD или DOA с вершиной О

3 угол: угол AED или DEA с вершиной Е

4 угол: угол BCD или DCB с вершиной С

Поделись с друзьями в социальных сетях:

Источник

{} набор набор элементов A = {3,7,9,14},
B = {9,14,28} А ∩ Б пересечение объекты, принадлежащие множеству A и множеству B A ∩ B = {9,14} А ∪ Б союз объекты, принадлежащие множеству A или множеству B A ∪ B = {3,7,9,14,28} А ⊆ Б подмножество A является подмножеством B. множество A включено в набор B. {9,14,28} ⊆ {9,14,28} A ⊂ B правильное подмножество / строгое подмножество A является подмножеством B, но A не равно B. {9,14} ⊂ {9,14,28} А ⊄ Б не подмножество множество A не является подмножеством множества B {9,66} ⊄ {9,14,28} А ⊇ Б суперсет A является надмножеством B. множество A включает множество B {9,14,28} ⊇ {9,14,28} А ⊃ Б правильный суперсет / строгий суперсет A является надмножеством B, но B не равно A. {9,14,28} ⊃ {9,14} А ⊅ Б не суперсет множество A не является надмножеством множества B {9,14,28} ⊅ {9,66} 2 ^А набор мощности все подмножества A   набор мощности все подмножества A   А = В равенство оба набора имеют одинаковые элементы A = {3,9,14},
B = {3,9,14},
A = B А ^в дополнять все объекты, не принадлежащие множеству A   А Б относительное дополнение объекты, принадлежащие A, а не B A = {3,9,14},
B = {1,2,3},
AB = {9,14} А — Б относительное дополнение объекты, принадлежащие A, а не B A = {3,9,14},
B = {1,2,3},
AB = {9,14} A ∆ B симметричная разница объекты, принадлежащие A или B, но не их пересечение A = {3,9,14},
B = {1,2,3},
A ∆ B = {1,2,9,14} А ⊖ Б симметричная разница объекты, принадлежащие A или B, но не их пересечение A = {3,9,14},
B = {1,2,3},
A ⊖ B = {1,2,9,14} a ∈A элемент,
принадлежит установить членство A = {3,9,14}, 3 ∈ A x ∉A не элемент нет установленного членства A = {3,9,14}, 1 ∉ A ( а , б ) упорядоченная пара сборник из 2-х элементов   A × B декартово произведение множество всех упорядоченных пар из A и B   | A | мощность количество элементов множества A A = {3,9,14}, | A | = 3 #A мощность количество элементов множества A A = {3,9,14}, # A = 3 | вертикальная полоса такой, что А = {х | 3 <х <14} алеф-нуль бесконечная мощность множества натуральных чисел   алеф-он мощность множества счетных порядковых чисел   Ø пустой набор Ø = {} C = {Ø} универсальный набор набор всех возможных значений   ₀ набор натуральных / целых чисел (с нулем) ₀ = {0,1,2,3,4, …} 0 ∈ _{0 1} набор натуральных / целых чисел (без нуля) ₁ = {1,2,3,4,5, …} 6 ∈ ₁ набор целых чисел = {…- 3, -2, -1,0,1,2,3, …} -6 ∈ набор рациональных чисел = { x | x = a / b , a , b ∈ } 2/6 ∈ набор реальных чисел = { x | -∞ < х <∞} 6.343434∈ набор комплексных чисел = { z | z = a + bi , -∞ < a <∞, -∞ < b <∞} 6 + 2 i ∈

Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).

Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:

группа I — обозначения геометрических фигур и отношений между ними;

группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.

Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.

Группа I

СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ

А. Обозначение геометрических фигур

1. Геометрическая фигура обозначается — Ф.

2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:

А, В, С, D, … , L, М, N, …

1,2,3,4,…,12,13,14,…

3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:

а, b, с, d, … , l, m, n, …

Линии уровня обозначаются: h — горизонталь; f— фронталь.

Для прямых используются также следующие обозначения:

(АВ) — прямая, проходящая через точки А а В;

[АВ) — луч с началом в точке А;

[АВ] — отрезок прямой, ограниченный точками А и В.

4. Поверхности обозначаются строчными буквами греческого алфавита:

α, β, γ, δ,…,ζ,η,ν,…

Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:

α(а || b) — плоскость α определяется параллельными прямыми а и b;

β(d₁ d₂gα) — поверхность β определяется направляющими d₁ и d₂ , образующей g и плоскостью параллелизма α.

5. Углы обозначаются:

∠ABC — угол с вершиной в точке В, а также ∠α°, ∠β°, … , ∠φ°, …

6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:

— величина угла АВС;

— величина угла φ.

Прямой угол отмечается квадратом с точкой внутри

7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.

Например:

|АВ| — расстояние между точками А и В (длина отрезка АВ);

|Аа| — расстояние от точки А до линии a;

|Аα| — расстояшие от точки А до поверхности α;

|аb| — расстояние между линиями а и b;

|αβ| расстояние между поверхностями α и β.

8. Для плоскостей проекций приняты обозначения: π₁ и π₂,
где π₁ — горизонтальная плоскость проекций;

π₂ —фрюнтальная плоскость проекций.

При замене плоскостей проекций или введении новых плоскостей последние обозначают π₃, π₄ и т. д.

9. Оси проекций обозначаются: х, у, z, где х — ось абсцисс; у — ось ординат; z — ось аппликат.

Постояшную прямую эпюра Монжа обозначают k.

10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:

А’, В’, С’, D’, … , L’, М’, N’, горизонтальные проекции точек; А», В», С», D», … , L», М», N», … фронтальные проекции точек; a’ , b’ , c’ , d’ , … , l’, m’ , n’ , —
горизонтальные проекции линий; а» ,b» , с» , d» , … , l» , m» , n» , … фронтальные проекции линий; α’, β’, γ’, δ’,…,ζ’,η’,ν’,… горизонтальные проекции поверхностей;
α», β», γ», δ»,…,ζ»,η»,ν»,…
фронтальные проекции поверхностей.

11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса _0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.

Так: h_0α — горизонтальный след плоскости (поверхности) α;

f_0α — фронтальный след плоскости (поверхности) α.

12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.

Например: H_a — горизонтальный след прямой (линии) а;

F_a — фронтальный след прямой (линии ) a.

13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами _{1,2,3,…, n:}

А₁, А₂, А₃,…,А_n;

a₁, a₂, a₃,…,a_n;

α₁, α₂, α₃,…,α_n;

Ф₁, Ф₂, Ф₃,…,Ф_n и т. д.

Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом ₀:

A₀, B₀, С₀, D₀, …

Аксонометрические проекции

14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса ⁰:

А⁰, В⁰, С⁰, D⁰, …

1⁰, 2⁰, 3⁰, 4⁰, …

a⁰, b⁰, c⁰, d⁰, …

α⁰, β⁰, γ⁰, δ⁰, …

15. Вторичные проекции обозначаются путем добавления верхнего индекса ¹ :

А^{1 0}, В^{1 0}, С^{1 0}, D^{1 0}, …

1^{1 0}, 2^{1 0}, 3^{1 0}, 4^{1 0}, …

a^{1 0}, b^{1 0}, c^{1 0}, d^{1 0}, …

α^{1 0}, β^{1 0}, γ^{1 0}, δ^{1 0}, …

Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.

Б. Символы, обозначающие отношения между геометрическими фигурами

№ по пор.	Обозначение	Содержание	Пример символической записи
1	≡	Совпадают	(АВ)≡(CD) — прямая, проходящая через точки А и В, совпадает с прямой, проходящей через точки С и D
2	≅	Конгруентны	∠ABC≅∠MNK — угол АВС конгруентен углу MNK
3	∼	Подобны	ΔАВС∼ΔMNK — треугольники АВС и MNK подобны
4	||	Параллельны	α||β — плоскость α параллельна плоскости β
5	⊥	Перпендикулярны	а⊥b — прямые а и b перпендикулярны
6		Скрещиваются	с d — прямые с и d скрещиваются
7		Касательные	t l — прямая t является касательной к линии l. βα — плоскость β касательная к поверхности α
8	→	Отображаются	Ф1→Ф2 — фигура Ф1 отображается на фигуру Ф2
9	S	Центр проецирования. Если центр проецирования несобственная точка, то его положение обозначается стрелкой, указывающей направление проецирования	—
10	s	Направление проецирования	—
11	P	Параллельное проецирование	рsα Параллельное проецирование — параллельное проецирование на плоскость α в направлении s

В. Обозначения теоретико-множественные

№ по пор.	Обозначение	Содержание	Пример символической записи	Пример символической записи в геометрии
1	M,N	Множества	—	—
2	A,B,C,…	Элементы множества	—	—
3	{ … }	Состоит из …	Ф{A, B, C,… }	Ф{A, B, C,… } — фигура Ф состоит из точек А, В,С, …
4	∅	Пустое множество	L — ∅ — множество L пустое (не содержит элементов )	—
5	∈	Принадлежит, является элементом	2∈N (где N — множество натуральных чисел) — число 2 принадлежит множеству N	А ∈ а — точка А принадлежит прямой а (точка А лежит на прямой а )
6	⊂	Включает, cодержит	N⊂М — множество N является частью (подмножеством) множества М всех рациональных чисел	а⊂α — прямая а принадлежит плоскости α (понимается в смысле: множество точек прямой а является подмножеством точек плоскости α)
7	∪	Объединение	С = A U В — множество С есть объединение множеств A и В; {1, 2. 3, 4,5} = {1,2,3}∪{4,5}	ABCD = [AB] ∪ [ВС] ∪ [CD] — ломаная линия, ABCD есть объединение отрезков [АВ], [ВС], [CD]
8	∩	Пересечение множеств	М=К∩L — множество М есть пересечение множеств К и L (содержит в себе элементы, принадлежащие как множеству К, так и множеству L). М ∩ N = ∅— пересечение множеств М и N есть пустое множество (множества М и N не имеют общих элементов)	а = α ∩ β — прямая а есть пересечение плоскостей α и β а ∩ b = ∅ — прямые а и b не пересекаются (не имеют общих точек)

Группа II СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ

№ по пор.	Обозначение	Содержание	Пример символической записи
1	∧	Конъюнкция предложений; соответствует союзу «и». Предложение (р∧q) истинно тогда и только тогда,когда р и q оба истинны	α∩β = { К:K∈α∧K∈β} Пересечение поверхностей α и β есть множество точек (линия), состоящее из всех тех и только тех точек К, которые принадлежат как поверхности α, так и поверхности β
2	∨	Дизъюнкция предложений; соответствует союзу «или». Предложение (p∨q) истинно, когда истинно хотя бы одно из предложений р или q (т. е. или р, или q, или оба).	—
3	⇒	Импликация — логическое следствие. Предложение р⇒q означает: «если р, то и q»	(а||с∧b||с)⇒a||b. Если две прямые параллельны третьей, то они параллельны между собой
4	⇔	Предложение (р⇔q) понимается в смысле: «если р, то и q; если q, то и р»	А∈α⇔А∈l⊂α. Точка принадлежит плоскости, если она принадлежит некоторой линии, принадлежащей этой плоскости. Справедливо также и обратное утверждение: если точка принадлежит некоторой линии, принадлежащей плоскости, то она принадлежит и самой плоскости
5	∀	Квантор общности, читается: для всякого, для всех, для любого. Выражение ∀(x)P(x) означает: «для всякого x: имеет место свойство Р(х) «	∀( ΔАВС)(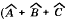 = 180°) Для всякого (для любого) треугольника сумма величин его углов при вершинах равна 180°
6	∃	Квантор существования, читается: существует. Выражение ∃(х)P(х) означает: «существует х, обладающее свойством Р(х)»	(∀α)(∃a)[a⊄α∧a||α].Для любой плоскости α существует прямая а, не принадлежащая плоскости α и параллельная плоскости α
7	∃1	Квантор единственности существования, читается: существует единственное (-я, -й)… Выражение ∃1(x)(Рх) означает: «существует единственное (только одно) х, обладающее свойством Рх»	(∀ А, В)(А≠B)(∃1а)(а∋А, В) Для любых двух различных точек А и В существует единственная прямая a, проходящая через эти точки.
8	(Px)	Отрицание высказывания P(x)	аb(∃α)(α⊃а, Ь).Если прямые а и b скрещиваются, то не существует плоскости а, которая содержит их
9		Отрицание знака	[AB]≠[CD] —отрезок [АВ] не равен отрезку [CD].а?b — линия а не параллельна линии b

Символьные обозначения Для обозначения геометрических фигур и их проекций, для отображения отношения между геометрическими фигурами, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем используются символьные обозначения. Символьные обозначения, все их многообразие, может быть подразделено на две группы: — Первая группа — обозначения геометрических фигур и отношения между ними; — Вторая группа — обозначения логических операций, составляющая синтаксическую основу геометрического языка. Символьные обозначения — Первая группа Символы, обозначающие геометрические фигуры и отношения между ними Обозначения геометрических фигур: Φ — геометрическая фигура; A, B, C, D, …, L, M, N, … — точки расположенные в пространстве; 1, 2, 3, 4, …, 12, 13, 14, … — точки расположенные в пространстве; a, b, c, d, …, l, m, n, … — линии, произвольно расположенные по отношению к плоскостям проекций; h, υ(f), ω — линии уровня (горизонталь, фронталь, профильная прямая соответственно); (AB) — прямая проходящая через точки A и B; [AB) — луч с началом в точке A; [AB] — отрезок прямой, ограниченный точками A и B; α, β, γ, δ, …, ζ, η, θ — поверхность; ∠ABC — угол с вершиной в точке B; ∠α, ∠β, ∠γ — угол α, угол β, угол γ соответственно; |AB| — расстояние от точки A до точки B (длина отрезка AB); |Aa| — расстояние от точки A до линии a; |Aα| — расстояние от точки A до поверхности α; |ab| — расстояние между прямыми a и b; |αβ| — расстояние между поверхностями α и β; H, V, W — координатные плоскости проекций (именуемые как горизонтальная, фронтальная, профильная соответственно); П1, П2, П3 — координатные плоскости проекций (именуемые как горизонтальная, фронтальная, профильная соответственно); x, y, z — координатные оси проекций (ось абсцисс, ось ординат, ось аппликат); ko — постоянная прямая эпюра Монжа; O — точка пересечения осей проекций; `, «, `» — верхние индексы для проекций точек, прямых, углов, фигур, поверхностей на плоскости проекций (именуемые как горизонтальную, фронтальную, профильную соответственно); 1, 2, 3 — верхние индексы для проекций точек, прямых, углов, фигур, поверхностей на плоскости проекций (именуемые как горизонтальную, фронтальную, профильную соответственно); αH, αV, αW — след поверхности оставляемый на горизонтальной, на фронтальной, на профильной плоскости проекций соответственно; αH, αV, αW — след поверхности α оставляемый на горизонтальной, на фронтальной, на профильной плоскости проекций соответственно; aH, aV, aW — след прямой a оставляемый на горизонтальной, на фронтальной, на профильной плоскости проекций соответственно; Проекции точек, линий, поверхностей любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса A`, A», A`» или 1`, 1″, 1`», соответствующего плоскости проекции, на которой они получены: A`, B`, C`, D`, …, L`, M`, N`, … — горизонтальные проекции точек; A», B», C», D», …, L», M», N», … — фронтальные проекции точек; A`», B`», C`», D`», …, L`», M`», N`», … — профильные проекции точек; a`, b`, c`, d`, …, l`, m`, n`, … — горизонтальные проекции линий; a», b», c», d», …, l», m», n», … — фронтальные проекции линий; a`», b`», c`», d`», …, l`», m`», n`», … — профильные проекции линий; α`, β`, γ`, δ`, …, ζ`, η`, θ`, … — горизонтальные проекции поверхностей; α», β», γ», δ», …, ζ», η», θ», … — фронтальные проекции поверхностей; α`», β`», γ`», δ`», …, ζ`», η`», θ`», … — профильные проекции поверхностей; Символы взаиморасположения геометрических объектов Обозначение   Смысловое значение   Пример символической записи   (…)   способ задания геометрического объекта в пространстве и на комплексном чертеже   А(А`, А») – точка А задана на комплексном чертеже горизонтальной и фронтальной проекциями; α(А, b) – плоскость α задана прямой b и точкой А.   ∈ ⊂ , ⊃   принадлежность   А∈l – точка А принадлежит прямой l; l⊂α – прямая l лежит в плоскости α   ≡   совпадение   А`≡ В` – горизонтальные проекции точек А и В совпадают.   ‖ , //   параллельность   a // b – прямые a и b параллельны.   ⊥   перпендикулярность   c⊥d – прямые c и d перпендикулярны.   ∸   скрещивание    m ∸ n – прямые m и n скрещивающиеся.    ∩   пересечение   k ∩ l – прямые k и l пересекаются.    ∾   подобие   ΔАВС ~ ΔDEF – треугольники ABC и DEF подобны.    ≅   конгруэнтность   ΔАВС ≅ /АВ/ = /CD/ – отрезки АВ и CD равны.    =    равенство, результат действия   /АВ/ = /CD/ – длины отрезков AB и CD равны; k ∩ l = M — прямые k и l пересекаются в точке M.    /   отрицание   А ∉ l – точка А не принадлежит прямой l.    → ←   отображение, преобразование   V/H → V1/H– система ортогональных плоскостей V/H преобразуется в систему плоскостей V1/H Символьные обозначения — Вторая группа Символы обозначающие логические операции    ∧   конъюнкция предложений (соответствует союзу «и»)   K ∈ a ∧ K ∈ d – точка K принадлежит прямым a и d    ∨   дизъюнкция предложений (соответствует союзу «или»)   А ∈ α ∨ A ∉ α – точка А принадлежит плоскости α или точка А не принадлежит плоскости α.    ⇒ ⇐   логическое следствие – импликация (следовательно, поэтому)    a // b ∧ c // b ⇒ a // c – прямые а и с параллельны прямой b, следовательно, они параллельны между собой.    ⇔   логическая эквивалентность (что то же самое) A ∈ l ⇔ A` ∈ l`, A» ∈ l» – точка А принадлежит прямой l, следовательно, ее проекции лежат на одноименных проекциях прямой; справедливо и обратное утверждение: проекции точки А лежат на одноименных проекциях прямой l, следовательно, точка принадлежит этой прямой. +