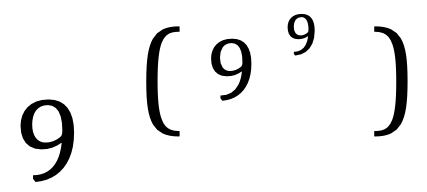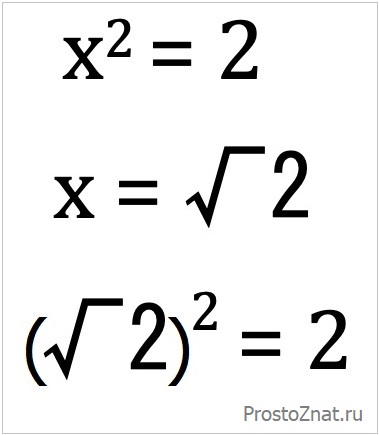Как пишутся миллионы цифрами

(Redirected from One Million)

← 999999 1000000 1000001 →
  • List of numbers
  • Integers

← 100 101 102 103 104 105 106 107 108 109
Cardinal one million
Ordinal 1000000th
(one millionth)
Factorization 26 × 56
Greek numeral {displaystyle {stackrel {rho }{mathrm {M} }}}
Roman numeral M
Binary 111101000010010000002
Ternary 12122102020013
Senary 332333446
Octal 36411008
Duodecimal 40285412
Hexadecimal F424016

Look up million in Wiktionary, the free dictionary.

One million (1,000,000), or one thousand thousand, is the natural number following 999,999 and preceding 1,000,001. The word is derived from the early Italian millione (milione in modern Italian), from mille, «thousand», plus the augmentative suffix -one.[1]

It is commonly abbreviated in British English as m[2][3][4] (not to be confused with the metric prefix «m», milli, for 10−3), M,[5][6] MM («thousand thousands», from Latin «Mille»; not to be confused with the Roman numeral MM = 2,000), mm (not to be confused with millimetre), or mn in financial contexts.[7][better source needed]

In scientific notation, it is written as 1×106 or 106.[8] Physical quantities can also be expressed using the SI prefix mega (M), when dealing with SI units; for example, 1 megawatt (1 MW) equals 1,000,000 watts.

The meaning of the word «million» is common to the short scale and long scale numbering systems, unlike the larger numbers, which have different names in the two systems.

The million is sometimes used in the English language as a metaphor for a very large number, as in «Not in a million years» and «You’re one in a million», or a hyperbole, as in «I’ve walked a million miles» and «You’ve asked a million-dollar question».

1,000,000 is also the square of 1000 and also the cube of 100.

Visualisation of powers of ten from 1 to 1 million

Visualizing one million[edit]

Even though it is often stressed that counting to precisely a million would be an exceedingly tedious task due to the time and concentration required, there are many ways to bring the number «down to size» in approximate quantities, ignoring irregularities or packing effects.

  • Information: Not counting spaces, the text printed on 136 pages of an Encyclopædia Britannica, or 600 pages of pulp paperback fiction contains approximately one million characters.
  • Length: There are one million millimetres in a kilometre, and roughly a million sixteenths of an inch in a mile (1 sixteenth = 0.0625). A typical car tire might rotate a million times in a 1,900-kilometre (1,200 mi) trip, while the engine would do several times that number of revolutions.
  • Fingers: If the width of a human finger is 22 mm (7⁄8 in), then a million fingers lined up would cover a distance of 22 km (14 mi). If a person walks at a speed of 4 km/h (2.5 mph), it would take them approximately five and a half hours to reach the end of the fingers.
  • Area: A square a thousand objects or units on a side contains a million such objects or square units, so a million holes might be found in less than three square yards of window screen, or similarly, in about one half square foot (400–500 cm2) of bed sheet cloth. A city lot 70 by 100 feet is about a million square inches.
  • Volume: The cube root of one million is one hundred, so a million objects or cubic units is contained in a cube a hundred objects or linear units on a side. A million grains of table salt or granulated sugar occupies about 64 mL (2.3 imp fl oz; 2.2 US fl oz), the volume of a cube one hundred grains on a side. One million cubic inches would be the volume of a small room 8+1⁄3 feet long by 8+1⁄3 feet wide by 8+1⁄3 feet high.
  • Mass: A million cubic millimetres (small droplets) of water would have a volume of one litre and a mass of one kilogram. A million millilitres or cubic centimetres (one cubic metre) of water has a mass of a million grams or one tonne.
  • Weight: A million 80-milligram (1.2 gr) honey bees would weigh the same as an 80 kg (180 lb) person.
  • Landscape: A pyramidal hill 600 feet (180 m) wide at the base and 100 feet (30 m) high would weigh about a million short tons.
  • Computer: A display resolution of 1,280 by 800 pixels contains 1,024,000 pixels.
  • Money: A USD bill of any denomination weighs 1 gram (0.035 oz). There are 454 grams in a pound. One million USD bills would weigh 1 megagram (1,000 kg; 2,200 lb) or 1 tonne (just over 1 short ton).
  • Time: A million seconds, 1 megasecond, is 11.57 days.

In Indian English and Pakistani English, it is also expressed as 10 lakh. Lakh is derived from lakṣa for 100,000 in Sanskrit.

One million black dots (pixels) – each tile with white or grey background contains 1000 dots (full image)

Selected 7-digit numbers (1,000,001–9,999,999)[edit]

1,000,001 to 1,999,999[edit]

  • 1,000,003 = Smallest 7-digit prime number
  • 1,000,405 = Smallest triangular number with 7 digits and the 1,414th triangular number
  • 1,002,001 = 10012, palindromic square
  • 1,006,301 = First number of the first pair of prime quadruplets occurring thirty apart ({1006301, 1006303, 1006307, 1006309} and {1006331, 1006333, 1006337, 1006339})[9]
  • 1,024,000 = Sometimes, the number of bytes in a megabyte[10]
  • 1,030,301 = 1013, palindromic cube
  • 1,037,718 = Large Schröder number
  • 1,048,576 = 10242 = 324 = 165 = 410 = 220, the number of bytes in a mebibyte (or often, a megabyte)
  • 1,048,976 = smallest 7 digit Leyland number
  • 1,058,576 = Leyland number
  • 1,058,841 = 76 x 32
  • 1,084,051 = fifth Keith prime[11]
  • 1,089,270 = harmonic divisor number[12]
  • 1,111,111 = repunit
  • 1,112,083 = logarithmic number[13]
  • 1,129,30832 + 1 is prime[14]
  • 1,136,689 = Pell number,[15] Markov number
  • 1,174,281 = Fine number[16]
  • 1,185,921 = 10892 = 334
  • 1,200,304 = 17 + 27 + 37 + 47 + 57 + 67 + 77 [17]
  • 1,203,623 = smallest unprimeable number ending in 3[18][19]
  • 1,234,321 = 11112, palindromic square
  • 1,262,180 = number of triangle-free graphs on 12 vertices[20]
  • 1,278,818 = Markov number
  • 1,299,709 = 100,000th prime number
  • 1,336,336 = 11562 = 344
  • 1,346,269 = Fibonacci number,[21] Markov number
  • 1,367,631 = 1113, palindromic cube
  • 1,413,721 = square triangular number[22]
  • 1,419,857 = 175
  • 1,421,280 = harmonic divisor number[12]
  • 1,441,440 = colossally abundant number,[23] superior highly composite number[24]
  • 1,441,889 = Markov number
  • 1,500,625 = 12252 = 354
  • 1,539,720 = harmonic divisor number[12]
  • 1,563,372 = Wedderburn-Etherington number[25]
  • 1,594,323 = 313
  • 1,596,520 = Leyland number
  • 1,606,137 = number of ways to partition {1,2,3,4,5,6,7,8,9} and then partition each cell (block) into subcells.[26]
  • 1,607,521/1,136,689 ≈ √2
  • 1,647,086 = Leyland number
  • 1,671,800 = Initial number of first century xx00 to xx99 consisting entirely of composite numbers[27]
  • 1,679,616 = 12962 = 364 = 68
  • 1,686,049 = Markov prime
  • 1,687,989 = number of square (0,1)-matrices without zero rows and with exactly 7 entries equal to 1[28]
  • 1,730,787 = Riordan number
  • 1,741,725 = equal to the sum of the seventh power of its digits
  • 1,771,561 = 13312 = 1213 = 116, also, Commander Spock’s estimate for the tribble population in the Star Trek episode «The Trouble with Tribbles»
  • 1,864,637 = k such that the sum of the squares of the first k primes is divisible by k.[29]
  • 1,874,161 = 13692 = 374
  • 1,889,568 = 185
  • 1,928,934 = 2 x 39 x 72
  • 1,941,760 = Leyland number
  • 1,953,125 = 1253 = 59

2,000,000 to 2,999,999[edit]

  • 2,000,002 = number of surface-points of a tetrahedron with edge-length 1000[30]
  • 2,000,376 = 1263
  • 2,012,174 = Leyland number
  • 2,012,674 = Markov number
  • 2,085,136 = 14442 = 384
  • 2,097,152 = 1283 = 87 = 221
  • 2,097,593 = Leyland prime[31]
  • 2,124,679 = largest known Wolstenholme prime[32]
  • 2,178,309 = Fibonacci number[21]
  • 2,222,222 = repdigit
  • 2,313,441 = 15212 = 394
  • 2,356,779 = Motzkin number[33]
  • 2,423,525 = Markov number
  • 2,476,099 = 195
  • 2,560,000 = 16002 = 404
  • 2,567,284 = number of partially ordered set with 10 unlabeled elements[34]
  • 2,646,723 = little Schroeder number
  • 2,674,440 = Catalan number[35]
  • 2,692,537 = Leonardo prime
  • 2,744,210 = Pell number[15]
  • 2,796,203 = Wagstaff prime,[36] Jacobsthal prime
  • 2,825,761 = 16812 = 414
  • 2,890,625 = 1-automorphic number[37]
  • 2,922,509 = Markov prime
  • 2,985,984 = 17282 = 1443 = 126 = 1,000,00012 AKA a great-great-gross

3,000,000 to 3,999,999[edit]

  • 3,111,696 = 17642 = 424
  • 3,200,000 = 205
  • 3,263,442 = product of the first five terms of Sylvester’s sequence
  • 3,263,443 = sixth term of Sylvester’s sequence[38]
  • 3,276,509 = Markov prime
  • 3,301,819 = alternating factorial[39]
  • 3,333,333 = repdigit
  • 3,360,633 = palindromic in 3 consecutive bases: 62818269 = 336063310 = 199599111
  • 3,418,801 = 18492 = 434
  • 3,426,576 = number of free 15-ominoes
  • 3,524,578 = Fibonacci number,[21] Markov number
  • 3,554,688 = 2-automorphic number[40]
  • 3,626,149 = Wedderburn–Etherington prime[25]
  • 3,628,800 = 10!
  • 3,748,096 = 19362 = 444
  • 3,880,899/2,744,210 ≈ √2

4,000,000 to 4,999,999[edit]

  • 4,008,004 = 20022, palindromic square
  • 4,037,913 = sum of the first ten factorials
  • 4,084,101 = 215
  • 4,100,625 = 20252 = 454
  • 4,194,304 = 20482 = 411 = 222
  • 4,194,788 = Leyland number
  • 4,208,945 = Leyland number
  • 4,210,818 = equal to the sum of the seventh powers of its digits
  • 4,213,597 = Bell number[41]
  • 4,260,282 = Fine number[42]
  • 4,297,512 = 12-th derivative of xx at x=1[43]
  • 4,324,320 = colossally abundant number,[23] superior highly composite number,[24] pronic number
  • 4,400,489 = Markov number
  • 4,444,444 = repdigit
  • 4,477,456 = 21162 = 464
  • 4,782,969 = 21872 = 97 = 314
  • 4,782,974 = n such that n | (3n + 5)[44]
  • 4,785,713 = Leyland number
  • 4,805,595 = Riordan number
  • 4,826,809 = 21972 = 1693 = 136
  • 4,879,681 = 22092 = 474

5,000,000 to 5,999,999[edit]

  • 5,134,240 = the largest number that cannot be expressed as the sum of distinct fourth powers
  • 5,153,632 = 225
  • 5,221,225 = 22852, palindromic square
  • 5,293,446 = Large Schröder number
  • 5,308,416 = 23042 = 484
  • 5,496,925 = first cyclic number in base 6
  • 5,555,555 = repdigit
  • 5,702,887 = Fibonacci number[21]
  • 5,761,455 = The number of primes under 108
  • 5,764,801 = 24012 = 494 = 78
  • 5,882,353 = 5882 + 23532

6,000,000 to 6,999,999[edit]

  • 6,250,000 = 25002 = 504
  • 6,436,343 = 235
  • 6,536,382 = Motzkin number[33]
  • 6,625,109 = Pell number,[15] Markov number
  • 6,666,666 = repdigit
  • 6,765,201 = 26012 = 514
  • 6,948,496 = 26362, palindromic square

7,000,000 to 7,999,999[edit]

  • 7,109,376 = 1-automorphic number[37]
  • 7,311,616 = 27042 = 524
  • 7,453,378 = Markov number
  • 7,529,536 = 27442 = 1963 = 146
  • 7,652,413 = Largest n-digit pandigital prime
  • 7,777,777 = repdigit
  • 7,779,311 = A hit song written by Prince and released in 1982 by The Time
  • 7,861,953 = Leyland number
  • 7,890,481 = 28092 = 534
  • 7,906,276 = pentagonal triangular number
  • 7,913,837 = Keith number[11]
  • 7,962,624 = 245

8,000,000 to 8,999,999[edit]

  • 8,000,000 = Used to represent infinity in Japanese mythology
  • 8,108,731 = repunit prime in base 14
  • 8,388,607 = second composite Mersenne number with a prime exponent
  • 8,388,608 = 223
  • 8,389,137 = Leyland number
  • 8,399,329 = Markov number
  • 8,436,379 = Wedderburn-Etherington number[25]
  • 8,503,056 = 29162 = 544
  • 8,675,309 = A hit song for Tommy Tutone (also a twin prime with 8,675,311)
  • 8,675,311 = Twin prime with 8,675,309
  • 8,888,888 = repdigit
  • 8,946,176 = self-descriptive number in base 8

9,000,000 to 9,999,999[edit]

  • 9,150,625 = 30252 = 554
  • 9,227,465 = Fibonacci number,[21] Markov number
  • 9,369,319 = Newman–Shanks–Williams prime[45]
  • 9,647,009 = Markov number
  • 9,653,449 = square Stella octangula number
  • 9,581,014 = n such that n | (3n + 5)[46]
  • 9,663,500 = Initial number of first century xx00 to xx99 that possesses an identical prime pattern to any century with four or fewer digits: its prime pattern of {9663503, 9663523, 9663527, 9663539, 9663553, 9663581, 9663587} is identical to {5903, 5923, 5927, 5939, 5953, 5981, 5987}[47][48]
  • 9,694,845 = Catalan number[35]
  • 9,699,690 = eighth primorial
  • 9,765,625 = 31252 = 255 = 510
  • 9,800,817 = equal to the sum of the seventh powers of its digits
  • 9,834,496 = 31362 = 564
  • 9,865,625 = Leyland number
  • 9,926,315 = equal to the sum of the seventh powers of its digits
  • 9,938,375 = 2153, the largest 7-digit cube
  • 9,997,156 = largest triangular number with 7 digits and the 4,471st triangular number
  • 9,998,244 = 31622, the largest 7-digit square
  • 9,999,991 = Largest 7-digit prime number
  • 9,999,999 = repdigit

See also[edit]

  • Huh (god), depictions of whom were also used in hieroglyphs to represent one million
  • Megagon
  • Millionaire
  • Names of large numbers
  • Orders of magnitude (numbers) to help compare dimensionless numbers between 1,000,000 and 10,000,000 (106 and 107)

.

References[edit]

  1. ^ «million». Dictionary.com Unabridged. Random House, Inc. Retrieved 4 October 2010.
  2. ^ «m». Oxford Dictionaries. Oxford University Press. Archived from the original on July 6, 2012. Retrieved 2015-06-30.
  3. ^ «figures». The Economist Style Guide (11th ed.). The Economist. 2015. ISBN 9781782830917.
  4. ^ «6.7 Abbreviating ‘million’ and ‘billion’«. English Style Guide. A handbook for authors and translators in the European Commission (PDF) (2019 ed.). 26 February 2019. p. 37.
  5. ^ «m». Merriam-Webster. Merriam-Webster Inc. Retrieved 2015-06-30.
  6. ^ «Definition of ‘M’«. Collins English Dictionary. HarperCollins Publishers. Retrieved 2015-06-30.
  7. ^ Averkamp, Harold. «Q&A: What Does M and MM Stand For?». AccountingCoach.com. AccountingCoach, LLC. Retrieved 25 June 2015.
  8. ^ David Wells (1987). The Penguin Dictionary of Curious and Interesting Numbers. London: Penguin Group. p. 185. 1,000,000 = 106
  9. ^ Sloane, N. J. A. (ed.). «Sequence A059925 (Initial members of two prime quadruples (A007530) with the smallest possible difference of 30.)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2019-01-27.
  10. ^ Tracing the History of the Computer — History of the Floppy Disk
  11. ^ a b «Sloane’s A007629 : Repfigit (REPetitive FIbonacci-like diGIT) numbers (or Keith numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  12. ^ a b c «Sloane’s A001599 : Harmonic or Ore numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  13. ^ Sloane, N. J. A. (ed.). «Sequence A002104 (Logarithmic numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  14. ^ Sloane, N. J. A. (ed.). «Sequence A006315 (Numbers n such that n^32 + 1 is prime)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  15. ^ a b c «Sloane’s A000129 : Pell numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  16. ^ Sloane, N. J. A. (ed.). «Sequence A000957». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-06-01.
  17. ^ Sloane, N. J. A. (ed.). «Sequence A031971». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  18. ^ Collins, Julia (2019). Numbers in Minutes. United Kingdom: Quercus. p. 140. ISBN 978-1635061772.
  19. ^ Sloane, N. J. A. (ed.). «Sequence A143641 (Odd prime-proof numbers not ending in 5)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  20. ^ Sloane, N. J. A. (ed.). «Sequence A006785 (Number of triangle-free graphs on n vertices)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  21. ^ a b c d e «Sloane’s A000045 : Fibonacci numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  22. ^ «Sloane’s A001110 : Square triangular numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  23. ^ a b «Sloane’s A004490 : Colossally abundant numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  24. ^ a b «Sloane’s A002201 : Superior highly composite numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  25. ^ a b c «Sloane’s A001190 : Wedderburn-Etherington numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  26. ^ Sloane, N. J. A. (ed.). «Sequence A000258 (Expansion of e.g.f. exp(exp(exp(x)-1)-1))». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  27. ^ Sloane, N. J. A. (ed.). «Sequence A181098 (Primefree centuries)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2019-01-27.
  28. ^ Sloane, N. J. A. (ed.). «Sequence A122400 (Number of square (0,1)-matrices without zero rows and with exactly n entries equal to 1)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  29. ^ Sloane, N. J. A. (ed.). «Sequence A111441 (Numbers k such that the sum of the squares of the first k primes is divisible by k)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-06-02.
  30. ^ Sloane, N. J. A. (ed.). «Sequence A005893 (Number of points on surface of tetrahedron)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  31. ^ «Sloane’s A094133 : Leyland primes». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  32. ^ «Wolstenholme primes». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  33. ^ a b «Sloane’s A001006 : Motzkin numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  34. ^ Sloane, N. J. A. (ed.). «Sequence A000112 (Number of partially ordered sets (posets) with n unlabeled elements)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  35. ^ a b «Sloane’s A000108 : Catalan numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  36. ^ «Sloane’s A000979 : Wagstaff primes». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  37. ^ a b Sloane, N. J. A. (ed.). «Sequence A003226 (Automorphic numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2019-04-06.
  38. ^ «Sloane’s A000058 : Sylvester’s sequence». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  39. ^ «Sloane’s A005165 : Alternating factorials». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  40. ^ Sloane, N. J. A. (ed.). «Sequence A030984 (2-automorphic numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2021-09-01.
  41. ^ «Sloane’s A000110 : Bell or exponential numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  42. ^ Sloane, N. J. A. (ed.). «Sequence A000957». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-06-01.
  43. ^ Sloane, N. J. A. (ed.). «Sequence A005727». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  44. ^ Sloane, N. J. A. (ed.). «Sequence A277288 (Positive integers n such that n)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  45. ^ «Sloane’s A088165 : NSW primes». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  46. ^ Sloane, N. J. A. (ed.). «Sequence A277288 (Positive integers n such that n)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  47. ^ «First pair of primes (p1, p2) that begin centuries of primes having the same prime configuration, ordered by increasing p2. Each configuration is allowed only once». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-07-03.
  48. ^ Sloane, N. J. A. (ed.). «Sequence A258275 (Smallest number k > n such that the interval k*100 to k*100+99 has exactly the same prime pattern as the interval n*100 to n*100+99)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
Источник

(Redirected from One Million)

← 999999 1000000 1000001 →
  • List of numbers
  • Integers

← 100 101 102 103 104 105 106 107 108 109
Cardinal one million
Ordinal 1000000th
(one millionth)
Factorization 26 × 56
Greek numeral {displaystyle {stackrel {rho }{mathrm {M} }}}
Roman numeral M
Binary 111101000010010000002
Ternary 12122102020013
Senary 332333446
Octal 36411008
Duodecimal 40285412
Hexadecimal F424016

Look up million in Wiktionary, the free dictionary.

One million (1,000,000), or one thousand thousand, is the natural number following 999,999 and preceding 1,000,001. The word is derived from the early Italian millione (milione in modern Italian), from mille, «thousand», plus the augmentative suffix -one.[1]

It is commonly abbreviated in British English as m[2][3][4] (not to be confused with the metric prefix «m», milli, for 10−3), M,[5][6] MM («thousand thousands», from Latin «Mille»; not to be confused with the Roman numeral MM = 2,000), mm (not to be confused with millimetre), or mn in financial contexts.[7][better source needed]

In scientific notation, it is written as 1×106 or 106.[8] Physical quantities can also be expressed using the SI prefix mega (M), when dealing with SI units; for example, 1 megawatt (1 MW) equals 1,000,000 watts.

The meaning of the word «million» is common to the short scale and long scale numbering systems, unlike the larger numbers, which have different names in the two systems.

The million is sometimes used in the English language as a metaphor for a very large number, as in «Not in a million years» and «You’re one in a million», or a hyperbole, as in «I’ve walked a million miles» and «You’ve asked a million-dollar question».

1,000,000 is also the square of 1000 and also the cube of 100.

Visualisation of powers of ten from 1 to 1 million

Visualizing one million[edit]

Even though it is often stressed that counting to precisely a million would be an exceedingly tedious task due to the time and concentration required, there are many ways to bring the number «down to size» in approximate quantities, ignoring irregularities or packing effects.

  • Information: Not counting spaces, the text printed on 136 pages of an Encyclopædia Britannica, or 600 pages of pulp paperback fiction contains approximately one million characters.
  • Length: There are one million millimetres in a kilometre, and roughly a million sixteenths of an inch in a mile (1 sixteenth = 0.0625). A typical car tire might rotate a million times in a 1,900-kilometre (1,200 mi) trip, while the engine would do several times that number of revolutions.
  • Fingers: If the width of a human finger is 22 mm (7⁄8 in), then a million fingers lined up would cover a distance of 22 km (14 mi). If a person walks at a speed of 4 km/h (2.5 mph), it would take them approximately five and a half hours to reach the end of the fingers.
  • Area: A square a thousand objects or units on a side contains a million such objects or square units, so a million holes might be found in less than three square yards of window screen, or similarly, in about one half square foot (400–500 cm2) of bed sheet cloth. A city lot 70 by 100 feet is about a million square inches.
  • Volume: The cube root of one million is one hundred, so a million objects or cubic units is contained in a cube a hundred objects or linear units on a side. A million grains of table salt or granulated sugar occupies about 64 mL (2.3 imp fl oz; 2.2 US fl oz), the volume of a cube one hundred grains on a side. One million cubic inches would be the volume of a small room 8+1⁄3 feet long by 8+1⁄3 feet wide by 8+1⁄3 feet high.
  • Mass: A million cubic millimetres (small droplets) of water would have a volume of one litre and a mass of one kilogram. A million millilitres or cubic centimetres (one cubic metre) of water has a mass of a million grams or one tonne.
  • Weight: A million 80-milligram (1.2 gr) honey bees would weigh the same as an 80 kg (180 lb) person.
  • Landscape: A pyramidal hill 600 feet (180 m) wide at the base and 100 feet (30 m) high would weigh about a million short tons.
  • Computer: A display resolution of 1,280 by 800 pixels contains 1,024,000 pixels.
  • Money: A USD bill of any denomination weighs 1 gram (0.035 oz). There are 454 grams in a pound. One million USD bills would weigh 1 megagram (1,000 kg; 2,200 lb) or 1 tonne (just over 1 short ton).
  • Time: A million seconds, 1 megasecond, is 11.57 days.

In Indian English and Pakistani English, it is also expressed as 10 lakh. Lakh is derived from lakṣa for 100,000 in Sanskrit.

One million black dots (pixels) – each tile with white or grey background contains 1000 dots (full image)

Selected 7-digit numbers (1,000,001–9,999,999)[edit]

1,000,001 to 1,999,999[edit]

  • 1,000,003 = Smallest 7-digit prime number
  • 1,000,405 = Smallest triangular number with 7 digits and the 1,414th triangular number
  • 1,002,001 = 10012, palindromic square
  • 1,006,301 = First number of the first pair of prime quadruplets occurring thirty apart ({1006301, 1006303, 1006307, 1006309} and {1006331, 1006333, 1006337, 1006339})[9]
  • 1,024,000 = Sometimes, the number of bytes in a megabyte[10]
  • 1,030,301 = 1013, palindromic cube
  • 1,037,718 = Large Schröder number
  • 1,048,576 = 10242 = 324 = 165 = 410 = 220, the number of bytes in a mebibyte (or often, a megabyte)
  • 1,048,976 = smallest 7 digit Leyland number
  • 1,058,576 = Leyland number
  • 1,058,841 = 76 x 32
  • 1,084,051 = fifth Keith prime[11]
  • 1,089,270 = harmonic divisor number[12]
  • 1,111,111 = repunit
  • 1,112,083 = logarithmic number[13]
  • 1,129,30832 + 1 is prime[14]
  • 1,136,689 = Pell number,[15] Markov number
  • 1,174,281 = Fine number[16]
  • 1,185,921 = 10892 = 334
  • 1,200,304 = 17 + 27 + 37 + 47 + 57 + 67 + 77 [17]
  • 1,203,623 = smallest unprimeable number ending in 3[18][19]
  • 1,234,321 = 11112, palindromic square
  • 1,262,180 = number of triangle-free graphs on 12 vertices[20]
  • 1,278,818 = Markov number
  • 1,299,709 = 100,000th prime number
  • 1,336,336 = 11562 = 344
  • 1,346,269 = Fibonacci number,[21] Markov number
  • 1,367,631 = 1113, palindromic cube
  • 1,413,721 = square triangular number[22]
  • 1,419,857 = 175
  • 1,421,280 = harmonic divisor number[12]
  • 1,441,440 = colossally abundant number,[23] superior highly composite number[24]
  • 1,441,889 = Markov number
  • 1,500,625 = 12252 = 354
  • 1,539,720 = harmonic divisor number[12]
  • 1,563,372 = Wedderburn-Etherington number[25]
  • 1,594,323 = 313
  • 1,596,520 = Leyland number
  • 1,606,137 = number of ways to partition {1,2,3,4,5,6,7,8,9} and then partition each cell (block) into subcells.[26]
  • 1,607,521/1,136,689 ≈ √2
  • 1,647,086 = Leyland number
  • 1,671,800 = Initial number of first century xx00 to xx99 consisting entirely of composite numbers[27]
  • 1,679,616 = 12962 = 364 = 68
  • 1,686,049 = Markov prime
  • 1,687,989 = number of square (0,1)-matrices without zero rows and with exactly 7 entries equal to 1[28]
  • 1,730,787 = Riordan number
  • 1,741,725 = equal to the sum of the seventh power of its digits
  • 1,771,561 = 13312 = 1213 = 116, also, Commander Spock’s estimate for the tribble population in the Star Trek episode «The Trouble with Tribbles»
  • 1,864,637 = k such that the sum of the squares of the first k primes is divisible by k.[29]
  • 1,874,161 = 13692 = 374
  • 1,889,568 = 185
  • 1,928,934 = 2 x 39 x 72
  • 1,941,760 = Leyland number
  • 1,953,125 = 1253 = 59

2,000,000 to 2,999,999[edit]

  • 2,000,002 = number of surface-points of a tetrahedron with edge-length 1000[30]
  • 2,000,376 = 1263
  • 2,012,174 = Leyland number
  • 2,012,674 = Markov number
  • 2,085,136 = 14442 = 384
  • 2,097,152 = 1283 = 87 = 221
  • 2,097,593 = Leyland prime[31]
  • 2,124,679 = largest known Wolstenholme prime[32]
  • 2,178,309 = Fibonacci number[21]
  • 2,222,222 = repdigit
  • 2,313,441 = 15212 = 394
  • 2,356,779 = Motzkin number[33]
  • 2,423,525 = Markov number
  • 2,476,099 = 195
  • 2,560,000 = 16002 = 404
  • 2,567,284 = number of partially ordered set with 10 unlabeled elements[34]
  • 2,646,723 = little Schroeder number
  • 2,674,440 = Catalan number[35]
  • 2,692,537 = Leonardo prime
  • 2,744,210 = Pell number[15]
  • 2,796,203 = Wagstaff prime,[36] Jacobsthal prime
  • 2,825,761 = 16812 = 414
  • 2,890,625 = 1-automorphic number[37]
  • 2,922,509 = Markov prime
  • 2,985,984 = 17282 = 1443 = 126 = 1,000,00012 AKA a great-great-gross

3,000,000 to 3,999,999[edit]

  • 3,111,696 = 17642 = 424
  • 3,200,000 = 205
  • 3,263,442 = product of the first five terms of Sylvester’s sequence
  • 3,263,443 = sixth term of Sylvester’s sequence[38]
  • 3,276,509 = Markov prime
  • 3,301,819 = alternating factorial[39]
  • 3,333,333 = repdigit
  • 3,360,633 = palindromic in 3 consecutive bases: 62818269 = 336063310 = 199599111
  • 3,418,801 = 18492 = 434
  • 3,426,576 = number of free 15-ominoes
  • 3,524,578 = Fibonacci number,[21] Markov number
  • 3,554,688 = 2-automorphic number[40]
  • 3,626,149 = Wedderburn–Etherington prime[25]
  • 3,628,800 = 10!
  • 3,748,096 = 19362 = 444
  • 3,880,899/2,744,210 ≈ √2

4,000,000 to 4,999,999[edit]

  • 4,008,004 = 20022, palindromic square
  • 4,037,913 = sum of the first ten factorials
  • 4,084,101 = 215
  • 4,100,625 = 20252 = 454
  • 4,194,304 = 20482 = 411 = 222
  • 4,194,788 = Leyland number
  • 4,208,945 = Leyland number
  • 4,210,818 = equal to the sum of the seventh powers of its digits
  • 4,213,597 = Bell number[41]
  • 4,260,282 = Fine number[42]
  • 4,297,512 = 12-th derivative of xx at x=1[43]
  • 4,324,320 = colossally abundant number,[23] superior highly composite number,[24] pronic number
  • 4,400,489 = Markov number
  • 4,444,444 = repdigit
  • 4,477,456 = 21162 = 464
  • 4,782,969 = 21872 = 97 = 314
  • 4,782,974 = n such that n | (3n + 5)[44]
  • 4,785,713 = Leyland number
  • 4,805,595 = Riordan number
  • 4,826,809 = 21972 = 1693 = 136
  • 4,879,681 = 22092 = 474

5,000,000 to 5,999,999[edit]

  • 5,134,240 = the largest number that cannot be expressed as the sum of distinct fourth powers
  • 5,153,632 = 225
  • 5,221,225 = 22852, palindromic square
  • 5,293,446 = Large Schröder number
  • 5,308,416 = 23042 = 484
  • 5,496,925 = first cyclic number in base 6
  • 5,555,555 = repdigit
  • 5,702,887 = Fibonacci number[21]
  • 5,761,455 = The number of primes under 108
  • 5,764,801 = 24012 = 494 = 78
  • 5,882,353 = 5882 + 23532

6,000,000 to 6,999,999[edit]

  • 6,250,000 = 25002 = 504
  • 6,436,343 = 235
  • 6,536,382 = Motzkin number[33]
  • 6,625,109 = Pell number,[15] Markov number
  • 6,666,666 = repdigit
  • 6,765,201 = 26012 = 514
  • 6,948,496 = 26362, palindromic square

7,000,000 to 7,999,999[edit]

  • 7,109,376 = 1-automorphic number[37]
  • 7,311,616 = 27042 = 524
  • 7,453,378 = Markov number
  • 7,529,536 = 27442 = 1963 = 146
  • 7,652,413 = Largest n-digit pandigital prime
  • 7,777,777 = repdigit
  • 7,779,311 = A hit song written by Prince and released in 1982 by The Time
  • 7,861,953 = Leyland number
  • 7,890,481 = 28092 = 534
  • 7,906,276 = pentagonal triangular number
  • 7,913,837 = Keith number[11]
  • 7,962,624 = 245

8,000,000 to 8,999,999[edit]

  • 8,000,000 = Used to represent infinity in Japanese mythology
  • 8,108,731 = repunit prime in base 14
  • 8,388,607 = second composite Mersenne number with a prime exponent
  • 8,388,608 = 223
  • 8,389,137 = Leyland number
  • 8,399,329 = Markov number
  • 8,436,379 = Wedderburn-Etherington number[25]
  • 8,503,056 = 29162 = 544
  • 8,675,309 = A hit song for Tommy Tutone (also a twin prime with 8,675,311)
  • 8,675,311 = Twin prime with 8,675,309
  • 8,888,888 = repdigit
  • 8,946,176 = self-descriptive number in base 8

9,000,000 to 9,999,999[edit]

  • 9,150,625 = 30252 = 554
  • 9,227,465 = Fibonacci number,[21] Markov number
  • 9,369,319 = Newman–Shanks–Williams prime[45]
  • 9,647,009 = Markov number
  • 9,653,449 = square Stella octangula number
  • 9,581,014 = n such that n | (3n + 5)[46]
  • 9,663,500 = Initial number of first century xx00 to xx99 that possesses an identical prime pattern to any century with four or fewer digits: its prime pattern of {9663503, 9663523, 9663527, 9663539, 9663553, 9663581, 9663587} is identical to {5903, 5923, 5927, 5939, 5953, 5981, 5987}[47][48]
  • 9,694,845 = Catalan number[35]
  • 9,699,690 = eighth primorial
  • 9,765,625 = 31252 = 255 = 510
  • 9,800,817 = equal to the sum of the seventh powers of its digits
  • 9,834,496 = 31362 = 564
  • 9,865,625 = Leyland number
  • 9,926,315 = equal to the sum of the seventh powers of its digits
  • 9,938,375 = 2153, the largest 7-digit cube
  • 9,997,156 = largest triangular number with 7 digits and the 4,471st triangular number
  • 9,998,244 = 31622, the largest 7-digit square
  • 9,999,991 = Largest 7-digit prime number
  • 9,999,999 = repdigit

See also[edit]

  • Huh (god), depictions of whom were also used in hieroglyphs to represent one million
  • Megagon
  • Millionaire
  • Names of large numbers
  • Orders of magnitude (numbers) to help compare dimensionless numbers between 1,000,000 and 10,000,000 (106 and 107)

.

References[edit]

  1. ^ «million». Dictionary.com Unabridged. Random House, Inc. Retrieved 4 October 2010.
  2. ^ «m». Oxford Dictionaries. Oxford University Press. Archived from the original on July 6, 2012. Retrieved 2015-06-30.
  3. ^ «figures». The Economist Style Guide (11th ed.). The Economist. 2015. ISBN 9781782830917.
  4. ^ «6.7 Abbreviating ‘million’ and ‘billion’«. English Style Guide. A handbook for authors and translators in the European Commission (PDF) (2019 ed.). 26 February 2019. p. 37.
  5. ^ «m». Merriam-Webster. Merriam-Webster Inc. Retrieved 2015-06-30.
  6. ^ «Definition of ‘M’«. Collins English Dictionary. HarperCollins Publishers. Retrieved 2015-06-30.
  7. ^ Averkamp, Harold. «Q&A: What Does M and MM Stand For?». AccountingCoach.com. AccountingCoach, LLC. Retrieved 25 June 2015.
  8. ^ David Wells (1987). The Penguin Dictionary of Curious and Interesting Numbers. London: Penguin Group. p. 185. 1,000,000 = 106
  9. ^ Sloane, N. J. A. (ed.). «Sequence A059925 (Initial members of two prime quadruples (A007530) with the smallest possible difference of 30.)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2019-01-27.
  10. ^ Tracing the History of the Computer — History of the Floppy Disk
  11. ^ a b «Sloane’s A007629 : Repfigit (REPetitive FIbonacci-like diGIT) numbers (or Keith numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  12. ^ a b c «Sloane’s A001599 : Harmonic or Ore numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  13. ^ Sloane, N. J. A. (ed.). «Sequence A002104 (Logarithmic numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  14. ^ Sloane, N. J. A. (ed.). «Sequence A006315 (Numbers n such that n^32 + 1 is prime)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  15. ^ a b c «Sloane’s A000129 : Pell numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  16. ^ Sloane, N. J. A. (ed.). «Sequence A000957». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-06-01.
  17. ^ Sloane, N. J. A. (ed.). «Sequence A031971». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  18. ^ Collins, Julia (2019). Numbers in Minutes. United Kingdom: Quercus. p. 140. ISBN 978-1635061772.
  19. ^ Sloane, N. J. A. (ed.). «Sequence A143641 (Odd prime-proof numbers not ending in 5)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  20. ^ Sloane, N. J. A. (ed.). «Sequence A006785 (Number of triangle-free graphs on n vertices)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  21. ^ a b c d e «Sloane’s A000045 : Fibonacci numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  22. ^ «Sloane’s A001110 : Square triangular numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  23. ^ a b «Sloane’s A004490 : Colossally abundant numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  24. ^ a b «Sloane’s A002201 : Superior highly composite numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  25. ^ a b c «Sloane’s A001190 : Wedderburn-Etherington numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  26. ^ Sloane, N. J. A. (ed.). «Sequence A000258 (Expansion of e.g.f. exp(exp(exp(x)-1)-1))». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  27. ^ Sloane, N. J. A. (ed.). «Sequence A181098 (Primefree centuries)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2019-01-27.
  28. ^ Sloane, N. J. A. (ed.). «Sequence A122400 (Number of square (0,1)-matrices without zero rows and with exactly n entries equal to 1)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  29. ^ Sloane, N. J. A. (ed.). «Sequence A111441 (Numbers k such that the sum of the squares of the first k primes is divisible by k)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-06-02.
  30. ^ Sloane, N. J. A. (ed.). «Sequence A005893 (Number of points on surface of tetrahedron)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  31. ^ «Sloane’s A094133 : Leyland primes». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  32. ^ «Wolstenholme primes». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  33. ^ a b «Sloane’s A001006 : Motzkin numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  34. ^ Sloane, N. J. A. (ed.). «Sequence A000112 (Number of partially ordered sets (posets) with n unlabeled elements)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  35. ^ a b «Sloane’s A000108 : Catalan numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  36. ^ «Sloane’s A000979 : Wagstaff primes». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  37. ^ a b Sloane, N. J. A. (ed.). «Sequence A003226 (Automorphic numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2019-04-06.
  38. ^ «Sloane’s A000058 : Sylvester’s sequence». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  39. ^ «Sloane’s A005165 : Alternating factorials». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  40. ^ Sloane, N. J. A. (ed.). «Sequence A030984 (2-automorphic numbers)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2021-09-01.
  41. ^ «Sloane’s A000110 : Bell or exponential numbers». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  42. ^ Sloane, N. J. A. (ed.). «Sequence A000957». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-06-01.
  43. ^ Sloane, N. J. A. (ed.). «Sequence A005727». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  44. ^ Sloane, N. J. A. (ed.). «Sequence A277288 (Positive integers n such that n)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  45. ^ «Sloane’s A088165 : NSW primes». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-17.
  46. ^ Sloane, N. J. A. (ed.). «Sequence A277288 (Positive integers n such that n)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  47. ^ «First pair of primes (p1, p2) that begin centuries of primes having the same prime configuration, ordered by increasing p2. Each configuration is allowed only once». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2022-07-03.
  48. ^ Sloane, N. J. A. (ed.). «Sequence A258275 (Smallest number k > n such that the interval k*100 to k*100+99 has exactly the same prime pattern as the interval n*100 to n*100+99)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
Источник

Число 1000000 прописью: один миллион

Чётность числа: чётное
Сумма цифр: 1 + 0 + 0 + 0 + 0 + 0 + 0 = 1
Произведение цифр: 1 * 0 * 0 * 0 * 0 * 0 * 0 = 0
Целое число? Да
Натуральное число? Да
Произведение цифр (без 0): 1
Количество цифр: 7 (семизначное число)
Наибольшая цифра: 1
Наименьшая цифра: 0
Отрицательное число: -1000000
Цвет (rgb и hex): rgb(252, 93, 221) или #fcd5dd
PHP шифрование MD5: 8155bc545f84d9652f1012ef2bdfb6eb
SHA1-хэш: b27585828a675f5acfef052dd1a8cf0c6c1ee4b0
PHP Base64 encode: MTAwMDAwMA==
Синус числа в градусах: sin (1000000°) = -0.98480775301254
Синус числа в радианах: sin (1000000) = -0.34999350217129
Косинус числа в градусах: cos (1000000°) = 0.17364817766507
Косинус числа в радианах: cos (1000000) = 0.93675212753314
Тангенс числа в градусах: tan (1000000°) = -5.6712818196803
Тангенс числа в радианах: tan (1000000) = -0.3736244539876
Арктангенс числа в градусах: arctg (1000000°) = 1.5707390310154
Арктангенс числа в радианах: arctg (1000000) = 1.5707953267949
Число в квадрате: (1000000)2 = 1000000000000
Квадратный корень: 1000
Число в кубе: (1000000)3 = 1000000000000000000
Кубический корень: 100
Натуральный логарифм: 13.815510557964
Десятичный логарифм: 6
Модуль положительного числа: |1000000| = 1000000
Модуль отрицательного числа: |-1000000| = 1000000
В двоичном виде: 11110100001001000000
В восьмеричном виде: 3641100
В шестнадцатеричном виде (HEX): f4240
Перевод из байтов: 977 килобайтов
1000000 секунд это: 11 дней, 13 часов, 46 минут, 40 секунд
от 1000000 10,000.00
Нумерологическое сложение (редукция): ШАГ 1. 1+0+0+0+0+0+0 = 1
Значение числа 1: Власть, сила, мужественность, храбрость, жизнестойкость, лидерство.
1000000 римскими цифрами: I (1) (000) (000)
1000000 арабскими цифрами: ١٠٠٠٠٠٠
Число на английском языке прописью: one million

Таблица умножения на 1000000

1000000 * 1 = 1000000 (один миллион)
1000000 * 2 = 2000000 (два миллиона)
1000000 * 3 = 3000000 (три миллиона)
1000000 * 4 = 4000000 (четыре миллиона)
1000000 * 5 = 5000000 (пять миллионов)
1000000 * 6 = 6000000 (шесть миллионов)
1000000 * 7 = 7000000 (семь миллионов)
1000000 * 8 = 8000000 (восемь миллионов)
1000000 * 9 = 9000000 (девять миллионов)
1000000 * 10 = 10000000 (десять миллионов)
1000000 * 11 = 11000000 (одиннадцать миллионов)
1000000 * 12 = 12000000 (двенадцать миллионов)
1000000 * 13 = 13000000 (тринадцать миллионов)
1000000 * 14 = 14000000 (четырнадцать миллионов)
1000000 * 15 = 15000000 (пятнадцать миллионов)
1000000 * 16 = 16000000 (шестнадцать миллионов)
1000000 * 17 = 17000000 (семнадцать миллионов)
1000000 * 18 = 18000000 (восемнадцать миллионов)
1000000 * 19 = 19000000 (девятнадцать миллионов)
1000000 * 20 = 20000000 (двадцать миллионов)
1000000 * 21 = 21000000 (двадцать один миллион)
1000000 * 22 = 22000000 (двадцать два миллиона)
1000000 * 23 = 23000000 (двадцать три миллиона)
1000000 * 24 = 24000000 (двадцать четыре миллиона)
1000000 * 25 = 25000000 (двадцать пять миллионов)
1000000 * 26 = 26000000 (двадцать шесть миллионов)
1000000 * 27 = 27000000 (двадцать семь миллионов)
1000000 * 28 = 28000000 (двадцать восемь миллионов)
1000000 * 29 = 29000000 (двадцать девять миллионов)
1000000 * 30 = 30000000 (тридцать миллионов)
1000000 * 31 = 31000000 (тридцать один миллион)
1000000 * 32 = 32000000 (тридцать два миллиона)
1000000 * 33 = 33000000 (тридцать три миллиона)
1000000 * 34 = 34000000 (тридцать четыре миллиона)
1000000 * 35 = 35000000 (тридцать пять миллионов)
1000000 * 36 = 36000000 (тридцать шесть миллионов)
1000000 * 37 = 37000000 (тридцать семь миллионов)
1000000 * 38 = 38000000 (тридцать восемь миллионов)
1000000 * 39 = 39000000 (тридцать девять миллионов)
1000000 * 40 = 40000000 (сорок миллионов)
1000000 * 41 = 41000000 (сорок один миллион)
1000000 * 42 = 42000000 (сорок два миллиона)
1000000 * 43 = 43000000 (сорок три миллиона)
1000000 * 44 = 44000000 (сорок четыре миллиона)
1000000 * 45 = 45000000 (сорок пять миллионов)
1000000 * 46 = 46000000 (сорок шесть миллионов)
1000000 * 47 = 47000000 (сорок семь миллионов)
1000000 * 48 = 48000000 (сорок восемь миллионов)
1000000 * 49 = 49000000 (сорок девять миллионов)
1000000 * 50 = 50000000 (пятьдесят миллионов)
1000000 * 51 = 51000000 (пятьдесят один миллион)
1000000 * 52 = 52000000 (пятьдесят два миллиона)
1000000 * 53 = 53000000 (пятьдесят три миллиона)
1000000 * 54 = 54000000 (пятьдесят четыре миллиона)
1000000 * 55 = 55000000 (пятьдесят пять миллионов)
1000000 * 56 = 56000000 (пятьдесят шесть миллионов)
1000000 * 57 = 57000000 (пятьдесят семь миллионов)
1000000 * 58 = 58000000 (пятьдесят восемь миллионов)
1000000 * 59 = 59000000 (пятьдесят девять миллионов)
1000000 * 60 = 60000000 (шестьдесят миллионов)
1000000 * 61 = 61000000 (шестьдесят один миллион)
1000000 * 62 = 62000000 (шестьдесят два миллиона)
1000000 * 63 = 63000000 (шестьдесят три миллиона)
1000000 * 64 = 64000000 (шестьдесят четыре миллиона)
1000000 * 65 = 65000000 (шестьдесят пять миллионов)
1000000 * 66 = 66000000 (шестьдесят шесть миллионов)
1000000 * 67 = 67000000 (шестьдесят семь миллионов)
1000000 * 68 = 68000000 (шестьдесят восемь миллионов)
1000000 * 69 = 69000000 (шестьдесят девять миллионов)
1000000 * 70 = 70000000 (семьдесят миллионов)
1000000 * 71 = 71000000 (семьдесят один миллион)
1000000 * 72 = 72000000 (семьдесят два миллиона)
1000000 * 73 = 73000000 (семьдесят три миллиона)
1000000 * 74 = 74000000 (семьдесят четыре миллиона)
1000000 * 75 = 75000000 (семьдесят пять миллионов)
1000000 * 76 = 76000000 (семьдесят шесть миллионов)
1000000 * 77 = 77000000 (семьдесят семь миллионов)
1000000 * 78 = 78000000 (семьдесят восемь миллионов)
1000000 * 79 = 79000000 (семьдесят девять миллионов)
1000000 * 80 = 80000000 (восемьдесят миллионов)
1000000 * 81 = 81000000 (восемьдесят один миллион)
1000000 * 82 = 82000000 (восемьдесят два миллиона)
1000000 * 83 = 83000000 (восемьдесят три миллиона)
1000000 * 84 = 84000000 (восемьдесят четыре миллиона)
1000000 * 85 = 85000000 (восемьдесят пять миллионов)
1000000 * 86 = 86000000 (восемьдесят шесть миллионов)
1000000 * 87 = 87000000 (восемьдесят семь миллионов)
1000000 * 88 = 88000000 (восемьдесят восемь миллионов)
1000000 * 89 = 89000000 (восемьдесят девять миллионов)
1000000 * 90 = 90000000 (девяносто миллионов)
1000000 * 91 = 91000000 (девяносто один миллион)
1000000 * 92 = 92000000 (девяносто два миллиона)
1000000 * 93 = 93000000 (девяносто три миллиона)
1000000 * 94 = 94000000 (девяносто четыре миллиона)
1000000 * 95 = 95000000 (девяносто пять миллионов)
1000000 * 96 = 96000000 (девяносто шесть миллионов)
1000000 * 97 = 97000000 (девяносто семь миллионов)
1000000 * 98 = 98000000 (девяносто восемь миллионов)
1000000 * 99 = 99000000 (девяносто девять миллионов)
1000000 * 100 = 100000000 (сто миллионов)
Источник

Миллион

Миллион
1 000 000

один миллион
999 999 · 1 000 000 · 1 000 001
Факторизация: 2^6 cdot 5^6
Римская запись: Mn
Двоичное: 11110100001001000000
Восьмеричное: 3641100
Шестнадцатеричное: F4240
Натуральные числа

Миллион (сокращённо — млн; из фр. million[1], от ст.-итал. millione «большая тысяча»[2]) — тысяча тысяч, число, изображаемое единицей с шестью нулями, 106. В системе СИ числу соответствуют приставки: мега — для миллиона (106) и микро — для одной миллионной (10−6).

Часто в русском языке используется, как метафора для обозначения очень большого числа (количества) чего-либо.

Другие значения

  • С 1992 года в Даугавпилсе (Латвия) издаётся газета «Миллион»[3].

Интересные факты

  • В разговорной речи миллион денежных единиц с момента Октябрьской революции в периоды гиперинфляции (сразу после революции[4], в 1990-х и 2000-х годах) может заменяться сленговым словом лимон.
  • Не считая пробелов, текст на 136 страницах энциклопедии Britannica содержит около одного миллиона символов.
  • В километре один миллион миллиметров и примерно миллион шестнадцатых дюймов в миле. Обыкновенная автомобильная шина совершит миллион вращений, если проехать 1200 миль (1900 км), за это время двигатель успеет сделать в несколько раз больше оборотов, чем колесо.
  • Средняя ширина человеческого пальца 2,2225 см (7 / 8 дюйма), если миллион пальцев выложить по порядку то получится расстояние в 22 км (14миль). При средней скорости передвижения человека (4 км/ч) пришлось бы идти 5 или 6 часов.
  • Масса: миллион кубических миллиметров (один литр) воды имеет массу одного килограмма. Миллион миллилитров или кубических сантиметров (один кубический метр) воды имеет массу миллиона грамм или одной тонны.
  • Холм пирамидальной формы 600 футов (180 м) в ширину и в основании, 100 футов (30 м) в высоту будет весить около миллиона тонн.
  • Разрешение экрана 1280 на 800 содержит 1024000 пикселей.
  • Доллары любого наименования весят один грамм. В одном фунте 454 грамма. Один миллион долларовых купюр будет весить 2,204.62 фунтов, или чуть более 1 тонны.

См. также

  • Миллиард
  • Триллион

Примечания

  1. ↑ М. Фасмер. Этимологический словарь русского языка. Под ред. О. Н. Трубачёва. Москва, «Прогресс», 1986. Т. II, С. 621.
  2. ↑ A. Dauzat, J. Dubois, H. Mitterand. Nouveau Diccionaire Étymologique et Historique. Libraire Larousse, Paris, 1964. С. 465.
  3. ↑ million.lv (рус.) — официальный сайт газеты «Миллион»
  4. ↑ Маяковский В. В. Буржуй, прощайся с приятными деньками — добьём окончательно твёрдыми деньгами!
 Просмотр этого шаблона Числа с собственными именами
Вещественные Пи • Золотое сечение • Серебряное сечение • e (число Эйлера) • Постоянная Эйлера — Маскерони • Постоянные Фейгенбаума • Постоянная Гельфонда • Константа Бруна • Постоянная Каталана • Постоянная Апери
Натуральные Чёртова дюжина • Число зверя • Число Рамануджана — Харди • Число Грэма • Число Скьюза • Число Мозера
Степени десяти Мириада • Гугол • Асанкхейя • Гуголплекс
Степени тысячи Тысяча • Миллион • Миллиард • Биллион • Триллион • Квадриллион • … • Центиллион
Степени двенадцати Дюжина • Гросс • Масса

Категории:

  • Натуральные числа
  • Числа с собственными именами
  • Степени тысячи

Wikimedia Foundation.
2010.

Синонимы:

Полезное

Смотреть что такое «Миллион» в других словарях:

  • миллион — а, м. million m., пол. milion. 1. Число, равное тысяче тысяч; название числа 1.000. 000. БАС 1. ||. Количество чего л. в тысячу тысяч единиц. БАС 1. И награжден был <меньшиков> таким великим богатством, что приходов своих земель имел по… …   Исторический словарь галлицизмов русского языка

  • МИЛЛИОН — (фр., от ср. век. лат. millio). Тысяча тысяч. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. МИЛЛИОН тысяча тысяч. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907 …   Словарь иностранных слов русского языка

  • миллион — См …   Словарь синонимов

  • МИЛЛИОН — [или] и мильон, мильона, муж. (франц. million). 1. Число, равное тысяче тысяч (1000 000). 2. перен. Множество, бесконечное количество (разг.). «Пролетарская демократия в миллион раз демократичнее воякой буржуазной демократии…» Ленин. Толковый… …   Толковый словарь Ушакова

  • МИЛЛИОН — муж. тысяча тысяч. нный, к миллиону относящийся; миллион или миллионы в себе заключающий. Миллионер муж. рка жен. миллионщик муж. щица жен. богач, владеющий миллионом, миллионами. неров, неркин, щиков, щицын, ему, ей принадлежащий нерский, щичий …   Толковый словарь Даля

  • МИЛЛИОН — на миллион. Жарг. авиа. О хорошей, ясной погоде. Максимов, 248 …   Большой словарь русских поговорок

  • миллион —     МИЛЛИОН, разг. сниж. лимон …   Словарь-тезаурус синонимов русской речи

  • МИЛЛИОН — (франц. million) число, изображаемое в десятичной записи единицей с 6 нулями, т. е. число 106 …   Большой Энциклопедический словарь

  • МИЛЛИОН — [илио и ильё ], а, муж. Число и количество, равное тысяче тысяч. Миллионы людей (огромное множество). Нажить миллионы (огромные деньги; разг.). | прил. миллионный, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 …   Толковый словарь Ожегова

  • миллион — См. трамвай В. В. Виноградов. История слов, 2010 …   История слов

  • миллион — миллион. Произносится [милион] и допустимо [мильён] …   Словарь трудностей произношения и ударения в современном русском языке

Источник

Как правильно считать: 1 тысяча миллионов или один миллион миллиардов и как правильно записывать такие большие числа?

Для каждого такого числа есть свое специальное название – так, например, одна тысяча миллионов – это собственно один миллиард, а один миллион миллиардов – это один квадриллион. Более подробно о системе наименования чисел и ее вариациях можно почитать, например, хорошую статью на Википедии: https://ru.wikipedia.org/wiki/Системы_наименования_чисел

Что о жизни знают люди, у которых есть миллион долларов, чего не знают те, у кого миллиона нет?

Знаете, у меня была очень интересная ситуация, когда я с девушкой ловил такси, был дождь, другой город – Нью-Йорк, Манхэттен. И вдруг я вспомнил, что у меня в кармане только мелочь, а больше денег нет. Я залез, достал и посчитал их – у меня было 87 центов, до сих пор это помню. И я тогда одну вещь для себя вынес с тех времен – раньше я думал, что один доллар – это одна миллионная часть миллиона, а после этого момента я отчетливо и хорошо понял, что один доллар – это сто центов. Это философский ответ на многие вопросы, которые вы уже задали или еще не успели.

Источник статьи: http://yandex.ru/q/question/hw.math/kak_pravilno_schitat_1_tysiacha_millionov_040b9d6c/

Как правильно называются числа больше миллиарда

Ниже приведены название чисел, больших миллиона.

миллион 10⁶ = 1 000 000

миллиард 10⁹ = 1 000 000 000

триллион 10¹² = 1 000 000 000 000

квадриллион 10¹⁵ = 1 000 000 000 000 000

квинтиллион 10¹⁸ = 1 000 000 000 000 000 000

секстиллион 10²¹ = 1 000 000 000 000 000 000 000

септиллион 10²⁴ = 1 000 000 000 000 000 000 000 000

октиллион 10²⁷ = 1 000 000 000 000 000 000 000 000 000

нониллион 10³⁰ = 1 000 000 000 000 000 000 000 000 000 000

дециллион 10³³ = 1 000 000 000 000 000 000 000 000 000 000 000

ундециллион 10³⁶ = 1 000 000 000 000 000 000 000 000 000 000 000

Как запомнить ?

Эти числа удобно запомнить если вы знакомы с названием цифр на латыни (приставки квадри- , квинти- , сексти – итд образованны от названий цифр 4, 5, 6 соответственно) . Эти цифры используются в названиях не просто так, и обозначают они число, которое нужно прибавить к единице в степени тысячи.

квадриллион (4 – quattuor) 1000¹⁺⁴ = 1000⁵ = 10¹⁵

Источник статьи: http://zen.yandex.ru/media/math/kak-pravilno-nazyvaiutsia-chisla-bolshe-milliarda-5b0ba7d3830905eda574948b

1000000 Руб. прописью

Сумма прописью ◄► один миллион рублей 00 копеек.

Почти все страны имеют свои деньги, и это не секрет. Все деньги мира имеют свой денежный знак. Рубли и копейки так называются деньги Российской федерации. Денежный знак рубля
1РУБ = 100 КОП

Рубль. Происхождение слово точно никто не знает, но есть три исторических варианта.

  1. Некоторые историки утверждают что, он произошёл от слова “рупия” – индийское слово.
  2. Есть ученные которые говорят что, рубль произошёл от слова “рубец” – Рубец на монете с боку оставался от заливки серебра в форму.
  3. Есть версия что, рубль произошёл от слова “рубить”. Некие историки утверждают что, раньше гривну рубили на четыре части, и эти четыре части называли рублями. А на арабском языке (руб.) означает четверть.

Если вы работайте с документами и приходится писать прописью суммы числа и. д. Тогда сохраните этот сайт в закладки он вам пригодится пять дней недели в рабочие дни. Внизу указаны суммы если хотите посмотреть как выглядит та или иная сумма прописью нажмите на то число. Все остальные числа которые появятся внизу кроме первого числа или цифры, больше на 1000000 руб. минимум на один и максимум на сорок девять.

Источник статьи: http://chislo-cifra.com/summa_propisyu.php?rub=1000000

Миллиард — это сколько?

Миллиард — это тысяча миллионов, или миллион тысяч. Миллиард записывается единицей с девятью нулями.

Это очень большое число, и его трудно себе представить. Например, за целый год не набежит миллиард секунд, и даже за 10 лет не набежит, и даже за 30. Миллиард секунд — это почти 32 года. За миллиард шагов можно дойти до Луны. А чтобы собрать компанию в миллиард человек понадобится 7 таких стран как Россия.

Миллиард — это исключительное название для большого числа. Все остальные большие числа заканчиваются на -он: миллион, триллион, квадриллион, квинтиллион. Тысячу миллионов стоило бы назвать биллионом, но как-то слово биллион не прижилось в русском языке, вместо биллиона говорят “миллиард”.

А знаешь, как называют число с сотней нулей? Гугол.

1 0 2 · Хороший ответ

Миллиард секунд это не 32 а почти 33 года , что-то около 32 лет 9 или 10 месяцев.

5 3 · Хороший ответ

Сколько всего тысяч в миллиарде?

Миллиард – это 1 000 000 000.

Нам надо узнать сколько раз надо взять 1000, чтобы получился 1 000 000 000.

1 000 000 000/1000 = 1 000 000

Ответ: В миллиарде миллион тысяч

2 9 · Хороший ответ

Что о жизни знают люди, у которых есть миллион долларов, чего не знают те, у кого миллиона нет?

Знаете, у меня была очень интересная ситуация, когда я с девушкой ловил такси, был дождь, другой город – Нью-Йорк, Манхэттен. И вдруг я вспомнил, что у меня в кармане только мелочь, а больше денег нет. Я залез, достал и посчитал их – у меня было 87 центов, до сих пор это помню. И я тогда одну вещь для себя вынес с тех времен – раньше я думал, что один доллар – это одна миллионная часть миллиона, а после этого момента я отчетливо и хорошо понял, что один доллар – это сто центов. Это философский ответ на многие вопросы, которые вы уже задали или еще не успели.

3 5 8 · Хороший ответ

Сколько нулей в Гуголплексе?

Гуглоплекс – это число 10 в степени гугол. Гугол – это единица со ста нулями (10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000).

7 9 · Хороший ответ

Реально ли стать миллионером, если собрать с каждого жителя России по рублю? И как это сделать?

НАДО СОБРАТЬ ГРУППУ ЛЮДЕЙ В ИНТЕРНЕТЕ ОБГОВАРИТЬ ДЕТАЛИ НАЗНАЧИТЬ ЧЕЛОВЕКА КТО БУДЕТ СОБИРАТЬ ДЕНЬГИ ОБЩИЕ ДЛЯ ГРУППЫ И ПОТОМ БУДЕТ ВЫДАВАТЬ НА 1 УЧАСТНИКА ГРУППЫ! Группа должна быть не меньше 1 миллиона человек! Чтобы скидываться по 1 рублю с каждого участника! От 1 рубля не обиднеем! Возмём пример: соц.сети в контакте раньше 30 рублей за регистрацию за 1 человека брали, одноклассники за подарки берут от 1 до 75 ок за 1 подарок! Сколько соц. сети делают денег? Блогерши имеют больше 1 миллиона подписчиков и считают людей нищебродами! Государство давно играет с миру по нитке только по 13% с рабочего человека, а мало кто до пенсии доживает до 65 лет! Здесь есть над чем подумать? Уж по 1 рублю скинуться для одного человека которому нужна финансовая помощь закрыть кредит или ипотеку, сделать человека счастливым, никакого напряга не вижу, тем более на 1 рубль ничего не купишь,учитывая что в нашей стране есть миллиордеры. Есть возможность это исправить действовать всем вместе слажено и не бояться организовать в сети сообщество, (группу)добавляться в сообщество в группу выбрать 1 участника сообщества кому нужна помощь, он выставит счёт и на этот счёт перечислять деньги, потом найти 2- го участника группы он тоже выставит счёт и ему тоже перечислять всей групой по 1 рублю и т.д. и тогда всё получиться, можно делать откат 10% в благотворительный фонд помощь детям!

Источник статьи: http://yandex.ru/q/question/science/milliard_eto_skolko_e695899f/

Сумма прописью онлайн

Чтобы узнать результат перевода, введите сумму

Бесплатный калькулятор “Сумма прописью онлайн” поможет быстро перевести сумму, записанную цифрами, в сумму прописью по всем правилам орфографии. Правописание числительных — обширная тема с массой нюансов, не все помнят ее со школы. Наш простой калькулятор покажет суммы прописью на русском языке без ошибок. Вам нужно только ввести цифровое значение в поле.

При заполнении финансовых, бухгалтерских и налоговых документов нужно написать денежный показатель цифрами и продублировать его прописью — то есть, прописать словами. Это делается в зарплатных ведомостях, договорах, кассовых ордерах, применяется для банковского чека — деньги фигурируют почти во всех бумагах. Основная цель прописывания сумм — желание избежать подделки. Внешний вид цифр легко изменить, а вот словесное написание исправить трудно.

Перевод цифровых значений в словесные — утомительное занятие. Если вам приходится заполнять много документов, то возрастает и риск ошибки. Чтобы легко и бесплатно перевести сумму в правильный прописной вариант, воспользуйтесь нашим калькулятором.

Как работает калькулятор «Сумма прописью онлайн»

Введите числовой вариант суммы в рублях в поле калькулятора. Программа отреагирует на введение числа автоматически и предложит словесную формулировку суммы. Она будет писаться ниже числового поля сразу же после ввода цифр. Дополнительно ничего нажимать не нужно.

Прописная расшифровка появляется именно в том варианте, который принят для финансовых документов: рубли указываются прописью, копейки — цифрами, это правило. Сумма пишется с заглавной буквы, значение суммы в рублях и копейках не разделяется запятой или другим знаком препинания (точка, скобка). Например: “Двадцать тысяч пятьсот один рубль 51 копейка”.

Если нужно указать число копеек в сумме, пишите их после запятой или точки в составе числа. Пробел для этой цели использовать не удастся. Например: “20500,56” или “346.5”.

Если сумма целая, без копеек, пишите число без запятой и нулевых показателей после нее. Например: “3000000”. Калькулятор все поймет сам и предложит прописной вариант суммы с дополнением: “00 копеек”. Но и указание суммы в виде десятичной дроби с нулевыми значениями после запятой тоже допустимо. Например: “100,00”. Третий знак после запятой (точки) поставить не удастся.

Будьте внимательны, прописывая большие числа, особенно с несколькими нулями подряд.

Источник статьи: http://www.b-kontur.ru/profi/summa-propisyu

Как записать цифрами 5 миллиардов 9 миллионов 300 тысяч 7?

1 миллиард это девять нулей.

Первый 0 после единицы — это сотни миллионов

Второй — десятки миллионов

Четвертый — сотни тысяч

Пятый — десятки тысяч

5 миллиардов, значит, ставим 5 вместо единицы.

Сотен миллионов нет. Оставляем первый ноль.

Десятков миллионов тоже нет. Второй ноль тоже оставляем.

Вместо третьего нолика ставим 9.

В следующей тройке нулей три сотни тысяч. Ни десятков тысяч, ни тысяч.

И, наконец, к последним нулям. Сотен нет, десятков нет. Только 7 единиц.

Получается так: 5 009 300 007.

2 5 · Хороший ответ

Я нечего не поняла

500930007 помоему так если я не ошибаюсь ну вот сложите пять миллиардов плюс девять миллионов плюс триста тысяч плюс семь ответ 500930007 если я правильно понял

Один нуль пропустили. 5009300007

Советую разделять числа по разрядам,так удобнее записывать.

Сначала пишется милиард или класс более высший,то есть 9 миллиардов потом миллионы,если нету десятков и сотен миллионов,пропускаем их и пишем за них нули,и т.д

Вводите число и автоматом увидите пропись, калькулятор

Это выглядит так: 5 009 300 007

5 миллиардов: 5 000 000 000

5 миллиардов 9 миллионов: 5 009 000 000

5 миллиардов 9 миллионов 300 тысяч: 5 009 300 000

И 7. Ответ 5 009 300 007

Чему равно число Пи?

Никто не знает точно, чему равно пи. Если разделить длину окружности на ее диаметр, то результат всегда будет одинаковый, какую окружность ни возьми. Этот результат и обозначили греческой буквой пи. Буква понадобилась потому, что привычными цифрами это число точно записать невозможно. Но мы знаем, чему оно равно приблизительно.

Самое знаменитое приближение – 3,14. Чтобы запомнить больше цифр, можно выучить стишок:

Надо очень постараться

И запомнить всё как есть:

Три, четырнадцать, пятнадцать,

Девяносто два и шесть

2 1 5 · Хороший ответ

Сколько будет миллион умножить на миллион?

Получится миллион миллионов, или триллион.

Это число записывается единицей с двенадцатью нулями, оно огромно.

Во всей нашей галактике Млечный путь не наберется столько звезд. Зато на Земле растет примерно три триллиона деревьев, а в воде плавает примерно три триллиона рыб.

Можно еще вот как представить себе триллион: возьмем куб размерами 10 метров на 10 метров на 10 метров — в нем поместится несколько квартир. Разрежем этот куб на миллимитровые кубики, их как раз наберется триллион. Если эти кубики сложить в линию, ее длина будет миллион километров. Лентой такой длины можно 25 раз обмотать всю Землю по экватору.

2 9 · Хороший ответ

Как выиграть 1000000 р?

На этой площадке собраны хорошие казино, софт отменный, разработчики ПО известные, с хорошей отдачей, я рекомендую изучить рейтинг онлайн казино на реальные деньги. Он формируется на основе анализа скорости и честности выплат, оперативности работы службы поддержки, наличия лицензии, качества софта, бонусной программы и других немаловажных критериев. Переходи и выигравай! Удачи!

Как округлить до десятых числа: 16.88, 4.651, 1.29, 48.23, 36.96; до сотых число 8.636?

Чтобы округлить до десятых, нужно убрать после запятой все цифры, кроме одной.

Если следующая после остающейся цифра 0, 1, 2, 3 или 4, то цифру не изменяем.

Если следующая после остающейся – 5, 6, 7, 8 или 9, то цифру увеличиваем на единицу.

С сотыми по тому же принципу, только после запятой оставляем 2 цифры.

4 5 · Хороший ответ

В 2000-м за чертой бедности было более 40 млн, в 2018 их стало 18,9 млн. Но Путин всё равно виноват?

Данные устаревшие, но. лучше не стало:

За последние 20 лет с карты России исчезли 23 000 городов, сельских посёлков и деревень.

За последние 10 лет на 40% сократилось население на Дальнем Востоке и на 60% на Крайнем Севере.

Ежегодно Россия теряет по численности населения целую область равную Псковской или республику размером с Карелию, или такой крупный город, как Краснодар.

Каждую минуту в России умирает 5 человек, рождается только 3. Смертность превышает рождаемость в 1,7 раза, в отдельных регионах — в 2-3 раза.
26 000 детей ежегодно не доживают до 10 лет, ежедневно умирает 50 младенцев, 70% из них — в родильных домах.

Во всемирном рейтинге по уровню смертности Россия находится на 12-м месте с конца по соседству с Нигерией, Зимбабве, Чадом, Сомали.

По продолжительности жизни наша страна занимает 162-е место в мире позади Папуа-Новой Гвинеи и Гондураса.

Средняя продолжительность жизни российских мужчин — 59 лет (в странах ЕС — 79 лет, в США — 78, в Канаде — 81, в Японии — 82 года).

На 500 миллионов долларов, которые Роман Абрамович, разом, не считая ежемесячных гигантских выплат, вложил в развитие английского футбольного клуба, можно было построить 300 тысяч детских спортивных дворовых площадок в России (обустройство одной площадки обходится в 50 тысяч рублей).

По уровню расходов на здравоохранение Россия делит 112-114-е место в мире с Марокко и Эквадором — всего 5,3% ВВП против 9-11% ВВП в странах Западной Европы.

У американского президента одна загородная резиденция — в Кэмп-Дэвиде. У британского премьера тоже одна — в Чекерсе. У российского президента — резиденция «Русь» в Тверской области, подмосковные «Горки-9», «Барвиха», «Архангельское», «Ужин» на Валдае, «Шуйская чупа» в Карелии, «Волжский утес» в Самарской области, «Сосны» в Красноярском крае, «Ангарские хутора» под Иркутском, «Тантал» в Саратовской области… Одна только дача в Барвихе-4 занимает более шестидесяти гектаров, специальный отвод с Москва-реки… Одну только президентскую дачу «Русь» охраняют не менее шестисот человек…

На зимние Олимпийские игры в Сочи — любимый проект премьер-министра России Владимира Путина, который, как и Медведев, видит в них шанс продемонстрировать миру новую Россию — будет истрачено свыше 15 млрд. долларов. Для сравнения: Олимпиада в Ванкувере обошлась в два млрд. долларов, столько же стоили Олимпиады в Солт-Лейк Сити и в Турине.

Российские миллиардеры платят самые низкие в мире налоги (13%), которые не снились их коллегам во Франции и Швеции (57%), в Дании (61%), Италии (66%).

1,5% населения России владеют 50% национальных богатств.

60% населения вообще не имеют сбережений.

статья очень большая, целиком тут:

Статья устаревшая. Честно. В ней статистика 2012 года. Но за эти годы ситуация в стране лучше не стала. Там же сравнение данных с СССР. Данных по упадку. И Москва это совсем не показатель. Москва и область – это место куда соберут всех оставшихся, что бы прихлопнуть одним тапком. Уже половина тут толкается. Фактически сжимаемся в московское княжество обратно.

Источник статьи: http://yandex.ru/q/question/hw.math/kak_zapisat_tsiframi_5_milliardov_9_6ce57577/

Источник

Время чтения 11 мин.Просмотры 5к.

Мы живем среди понятных нам вещей и явлений. Мы привыкли к измерениям разных величин: расстояний, скоростей, объемов и прочего. Интуитивно понимаем разницу, если нам говорят, что одно в миллион раз больше другого. Ну, в миллион раз, и что тут такого?

Человек увеличен в миллион раз

Рис. 1. Человек, увеличенный в миллион раз (на рисунке 1959 года).

Содержание

  1. Как выглядит «больше в четверть миллионов раз»
  2. Кубическая миля: сколько в нее может поместиться
  3. Сравнение бесконечно больших и бесконечно малых величин
  4. Как пишется 1 миллион и больше
  5. Числа гиганты и миллионы миллионов
  6. Самое большое число, записанное тремя цифрами
  7. Уравнение икс в степени икс
  8. О расчете электрических цепей

Как выглядит «больше в четверть миллионов раз»

Слово «миллион» означает тысячу тысяч, поэтому в миллионе всего шесть нулей после единицы – 1 000 000.

Четверть миллиона — это 1 000 000 разделить на 4, получается 250 тысяч или 250 000.

Однако, миллион – это все-таки много. Много настолько, что даже разница в размерах в четверть миллиона (примерно в 250 тысяч раз) дает нам просто несопоставимые размеры.

Допустим, мы представляем себе размеры дома. Большого ли маленького – именно, дома. Размеры дома не столь важны. Важно то, что весь земной шар, оказывается, в четверть миллиона раз больше, чем один среднестатистический дом.

Примерно в четверть миллиона раз наша Земля меньше, чем вся Солнечная система! То есть, если дважды увеличить размеры нашего среднего по величине дома в четверть миллиона раз, мы получим наше Солнце вместе с планетами Солнечной системы по линейному размеру. Речь идет именно о линейном размере в одном направлении, о размере, который мы измеряем с помощью линейки.

Кубическая миля: сколько в нее может поместиться

Объемы дома мы не сравниваем с объемами Земли или Солнечной системы. Мы сравниваем только их линейные размеры. Дело в том, что если говорить об объемах, то сопоставление будет еще больше, не в пользу дома. Здесь совсем другие числа. Какие? Давайте посмотрим.  В свое время ученые (возможно, английские!) подсчитали, что…

…Возьмем обычную географическую милю, равную по длине примерно 1855,4 метров – это протяженность одной минуты дуги вдоль экватора Земли. Мили до сих пор используют моряки, поскольку это очень удобно, если пользоваться  картами Земли.

Предположим, что мы можем сделать куб со сторонами, равными одной географической миле. Это значит, что куб должен быть всего-то по 1855 метров в каждом из 3-х направлений (длина, ширина, высота). Представим, что сможем сделать такой куб. Как Вы думаете, что внутри него может поместиться?!

… В середине прошлого столетия (1950-ые годы) делали такой подсчет. Так вот, в такой куб поместились бы одновременно:

  • все здания всего мира;
  • флоты всех государств;
  • все машины и сооружения со всех частей нашего света;
  • население всего земного шара;
  • все животные нашей планеты;
  • и еще в этом кубе осталось бы незаполненное свободное место!

Кстати, из вещества всего нашего земного шара можно (теоретически, конечно) изготовить 600 миллионов подобных ящиков. Тогда как все, что природой и людьми создано, помещается всего лишь в один из таких кубов!

кубическая миля

Рис. 2. Кубическая миля, как это может выглядеть.

Поэтому мы даже не говорим о сравнительных объемах вещей. Упоминаем только их линейные размеры.

Сравнение бесконечно больших и бесконечно малых величин

Попробуем  в порядке возрастания расположить линейные размеры известных нам предметов (и не очень известных).  При этом каждый последующий предмет должен быть в четверть миллиона раз больше (линейно, а не объемно!) предыдущего. Тогда можно составить следующий список:

  • электрон
  • атом
  • пылинка
  • дом
  • земной шар
  • солнечная система
  • расстояние до Полярной звезды
  • наша Галактика Млечный путь

Вот как получается, что если наш дом всего-то четырежды увеличить в четверть миллиона раз, то мы приблизимся к размеру всей нашей Галактики. А если дважды уменьшить в четверть миллиона раз, тогда дом превратится всего лишь в атом вещества!

Как еще можно представить себе миллион? Давайте попробуем:

  • полоса из миллиона волос, уложенных рядом друг с другом, была бы шириной около 100 метров;
  • если миллион раз зачерпнуть воду наперстком, можно вычерпать около тонны воды;
  • книга в миллион страниц была бы толщиной около 50 метров;
  • миллион букв помещаются в книге, размером около 600-800 страниц;
  • миллион дней – это 27 столетий (2700 лет), а мы живем пока только в 21-м столетии (закончился 2020 год) от начала новой эры.

книга из 10 000 листов

Рис. 3. В этой книге явно меньше миллиона листов.

Попробуем подсчитать количество страниц в книге, представленной на рисунке 3.

  • Пачка бумаги из 500 листов имеет толщину около 5 см.
  • Делим 500 листов на 5, это равно 100 листов. Получаем: 100 листов = 1 см.
  • 1 000 000 листов = 10 000 см или около 100 м.

Получается, что книга на рисунке содержит примерно 10 000 листов, что дает толщину книги примерно 1 метр.

Как пишется 1 миллион и больше

В миллионе шесть нулей после единицы. Цифрами миллион можно записать так: 1 000 000 (единица и шесть нулей после единицы).

Миллион двести пишется цифрами следующим образом: 1 000 200. Здесь после единицы идут три нуля и число двести – всего после единицы должно быть шесть цифр.

Два миллиона цифрами – это 2 000 000 (цифра два и шесть нулей после двойки).

Три миллиона пишется так: 3 000 000 (цифра три и шесть нулей после тройки).

Как пишется тысяча миллионов? Это миллион (шесть нулей после единицы), который нужно  умножить на тысячу (добавить еще три нуля справа). В сумме шесть и три нуля дают девять (6+3=9), получается миллиард – число с девятью нулями.

Тысяча миллионов – это миллиард, цифрами пишется так: 1 000 000 000 (после единицы девять нулей).

Числа гиганты и миллионы миллионов

Миллион – это очень много. А как быть с миллиардом, триллионом и другими числами гигантами? Это же еще больше!

В миллионе шесть нулей после единицы (1 000 000).

Дальше – больше: в миллиарде – девять нулей (1 000 000 000, тысяча миллионов).

В триллионе – 12 нулей (1 000 000 000 000, тысяча миллиардов или миллион миллионов).

Если, например, попытаться записать расстояние до самых отдаленных объектов нашей Вселенной, то мы получили бы число, примерно с 30-ю нулями (миллион триллион триллионов) – 6+12+12=30 нулей. А ведь такие большие расстояния измеряют не в метрах, а в световых годах, и это уже не более нескольких миллиардов.

Число молекул в одном кубическом метре газа – реально вычисленная величина – составляет не более чем число с 19-20-ю нулями (примерно сто миллиард миллиардов).

Ну, а если попытаться пересчитать все капли в океанах и морях Земли, то получится число с 27-28 нулями (около тысячи триллион триллионов). В общем, и не придумать ничего такого, что можно было бы посчитать с помощью огромных чисел с числом нулей, больше 30-и. А это где-то миллион триллион триллионов, но, может чуть больше!

Тем не менее, большие числа очень волнуют человечество. Даже понятие такое недавно появилось: big data – большие числа. Оно означает возможности обработки огромных массивов данных с помощью компьютеров.

Задачи big data состоит не в пересчете огромного количества чисел, а в обработке большого числа данных с тем, чтобы найти в них закономерности и затем использовать практически. Например, для выяснения предпочтений людей при выборе товаров и услуг, при поиске информации, при пользовании теми или иными сервисами. Но это, что называется, совсем другая история, с практическим финалом.

Самое большое число, записанное тремя цифрами

Вернемся просто к числам, без особой практической пользы, то есть, к абстрактным величинам. Как Вы думаете, какое самое большое число можно вот так запросто взять и записать, используя для этого всего 3 цифры? Оказывается, такое число записывается как девять в степени девять в степени девять:

Самое большое число из трех цифр

Рис. 4. Самое большое число, которое можно записать с помощью всего трех цифр.

Всего три девятки, а число получается фантастическое по своей величине! Начинается оно с цифр

428 124 773 175 747 048 036 987 118,

а заканчивается на 89. Что в середине этого числа, не знает никто! Потому что в этом числе 369 693 061 цифра! Более 369 миллионов цифр!

Древний Архимед известен много чем, и еще законом Архимеда. Когда-то он посчитал, что если весь мир (известный тогда) вплоть до неподвижных звезд (как тогда считалось) наполнить тончайшим песком, то получится количество песчинок в виде числа с 63-я цифрами. А здесь не 63 цифры, а почти 370 миллионов цифр!

Даже если пересчитать все электроны, что имеются в нашей Вселенной, мы не получим столь огромной величины. Вот так всего-то три цифры позволяют нам показать несоразмерной величины числа. И даже позволяют нам потом с этими числами оперировать.

Уравнение икс в степени икс

Рассмотрим, как люди легко оперируют с бесконечными числами. Когда-то в чести были не только цифровые компьютерные методы, но и аналитические, с помощью формул. Тогда существовали задачки, использующие бесконечно большие величины.

Например, предлагалось определить значение x (старое забытое школьное «икс»!) в выражении с бесконечным числом этих самых «иксов»:

уравнение икс возводим в степень икс бесконечно равно два

Рис. 5. Пример уравнения с бесконечным числом элементов. «Икс» возводим в степень «икс» бесконечное число раз, а в итоге получаем лишь «двоечку».

Как это ни странно, решается такое уравнение очень просто. Рассуждения следующие. Если число «иксов» бесконечно, то ничто не мешает нам приписать к этому бесконечному множеству «иксов» еще один «икс» – слева внизу от всей «плеяды иксов». Ведь от этого ничего не изменится, не правда ли? Бесконечное число «иксов» плюс еще один «икс» – все равно останется бесконечное число.

Ну, приписали, и что? Вспомним, что ранее записанная цепочка из бесконечного множества «иксов» равнялась 2, по условию задачи. И новая цепочка с дополнительным «иксом» слева тоже равна 2, поскольку новый «икс» ничего не поменял в бесконечности. А раз так, тогда можно запросто заменить всю старую цепочку из бесконечных «иксов» на одну единственную «двойку», ведь старая цепочка была равна 2!

В итоге получается на удивление просто: новый дополнительный «икс» станет у нас во второй степени. А результат будет равен двойке, как и раньше:

уравнение после обработки цепочки из бесконечного числа иксов

Рис. 6. Простейшее уравнение, которое получается в итоге, если правильно обработать цепочку из бесконечного числа «иксов».

Еще раз пройдемся по логике: «двоечка» над «иксом» – это та самая бесконечная плеяда «иксов», которая ранее была у нас равна двойке. Сам «икс» – это еще один приписанный нами «икс» к бесконечной цепочке «иксов», ведь от такой приписки ничего не меняется. А раз ничего не меняется, то полученный результат тоже не меняется, и он равен «двойке».

Получаем решение уравнения с бесконечным числом «иксов»:

Решение уравнения

Рис. 7. Решение простейшего уравнения (рис. 6), которое получилось в результате замены бесконечной цепочки «иксов» (рис. 5) на одну единственную «двойку».

Проверяем полученный ответ:

Проверка решения простого уравнения

Рис. 8. Проверка решения простейшего уравнения (рис. 6), полученного в результате обработки уравнения с бесконечным числом «иксов» (рис. 5).

О расчете электрических цепей

Вы спросите, зачем нужны задачки с бесконечными величинами, если в реальной жизни такого не бывает? Ошибаетесь, очень даже бывает. Поговорим немного о практической пользе операций с бесконечными числами. Например, энергетики легко оперируют с такими понятиями, как бесконечные электрические цепи (рис. 9).

бесконечная электрическая цепь с точки зрения энергетиков

Рис. 9. Вот так может выглядеть «бесконечная» электрическая цепь с точки зрения энергетиков.

Проложена, скажем, линия уличного освещения. Сколько ламп висит на различных столбах и иных подвесах? Очень много, особенно в больших городах. А как рассчитать такие электрические цепи? Вот именно – с помощью подобных только что продемонстрированных формул и с помощью подобных рассуждений!

Ход рассуждений – это когда к бесконечному числу электрических элементов легко приписывают дополнительные такие же элементы, а всю оставшуюся бесконечную цепь меняют на один единственный элемент. И далее без труда делают расчет значительно упростившейся электрической схемы.

В общем, как было показано, человечество давно перешагнуло за миллион, миллиард и триллион. И даже за пределы чисел с огромным количеством цифр, с сотнями миллионов. И спокойно себе работает, не то что работает, но и делает вполне реальные вещи там, где счет идет на бесконечные множества.

Но все-таки миллион – это так много! Зачем же тогда нужно все время больше и больше? Не правда ли?!

Источник

  • Как пишутся методические рекомендации
  • Как пишутся метастазы в заключении врача
  • Как пишутся месяца по английскому
  • Как пишутся месяца на английском языке
  • Как пишутся месяца года