Кто автор конических сечений древнегреческого сочинения о стереометрии

Впервые
конические сечения появились у Менехма
(IV
в. до н. э.), которой принимал параболу и
равностороннюю гиперболу для решения
задачи об удвоении куба ( см. §
6).
Он рассматривал остроугольный,
прямоугольный и тупоугольный конусы,
т. е. конусы, у которых угол при вершине
осевого сечения соответственно острый,
прямой или тупой, и каждый из них пересекал
плоскостью, перпендикулярной одной из
образующих. В первом случае в сечении
с поверхностью конуса получался эллипс
( рис. 19), во втором – парабола (рис.20), в
третьем – гипербола, точнее, одна, ветвь
гиперболы (рис 21).

Менехм
называл их сечениями соответственно
остроугольного, прямоугольного и
тупоугольного конуса. Фактически он
пользовался прямоугольными координатами
на плоскости: за начало координат
принимал вершину кривой второго порядка,
за одну из координатных осей – главный
диаметр, а другую ось проводил
перпендикулярно первой в плоскости, в
которой лежит кривая.

У
него встречается уравнение параболы в
виде

эллипса – в виде
и гиперболы

После
Менехма коническими сечениями в IV-III
вв. до н.э. занимались несколько ученых,
прежде всего Евклида и Архимед. Но
главной фигурой в этой области является
Аполлоний.

Аполлоний
Пергский (ок. 260-ок. 170) родился в г. Перги
в Малой Азии. Позднее он преподавал
математику и, возможно, астрономию в
Александрии. Основное его сочинение –
«Конические сечения». Другие сочинения,
меньшего масштаба – «О вставках», «О
касании», «О спиральных линиях» и др.

В
работе Аполлония «Конические сечения»
восемь книг; до наших дней сохранилось
семь. В сравнении с Менехмом он становится
на более общую точку зрения: берет
произвольный конус, причем рассматривает
две его полости, и пересекает конус
плоскостью под разными углами. В случае,
если плоскость пересекает все образующие
конуса, в ее пересечении с поверхностью
конуса образуется эллипс (рис. 22); если
она параллельна одной из образующих
конуса – парабола (рис. 23); если плоскость
пересекает обе полости конуса – гипербола
(рис.24).

Фактически
Аполлоний пользуется косоугольной
системой координат, принимая за начало
координат любую точку Р
кривой и направляя координатные оси
по диаметру и по касательной к кривой,
проходящих через точку Р.
В первой книге у него мы находим уравнение
параболы в виде
эллипса- в видеи гиперболы −данные отрезки. На выводе этих уравнений
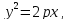
мы здесь не останавливаемся. (Проверьте,
что два последних уравнения можно
привести к форме, весьма близкой к
каноническим уравнениям эллипса и
гиперболы.

Сами
термины «парабола», «эллипс», «гипербола»
впервые встречаются у Аполлония. Слова
« парабола» в переводе с греческого
означает «приложение» : уравнение
читается словесно в виде равенства
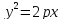
квадрата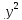и прямоугольника.Cлово
«эллипс» переводится как «недостаток»:
в правой части уравнения
не хватает слагаемогодля того, чтобы получилось «приложение»,
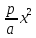
как в уравненииСлово «гипербола» -«избыток»: в правой
части уравнениянужно отбросить лишнее слагаемоедля того, чтобы можно было оставить
«приложение».

Символики
у Аполлония нет; доказательства проводятся
словесно. При доказательствах регулярно
применяется геометрическая алгебра,
которой пользовался еще Евклид (см. §
10). Постоянные
в уравнениях конических сечений
вводились, в частности, для того, чтобы
уравнять размерности левой и правой
частей. Доказательства во многих случаях
получались весьма непростыми.

Далее
в первой части Аполлоний рассматривает
касательные к коническому сечению,
направления хорд кривой, сопряженных
с любым диаметром, и др. Затем он
преобразует уравнения эллипса и гиперболы
так, что начало координат совпадало с
вершиной параболы. Наконец, он связывает
свои уравнения конических сечений с
уравнениями Менехма.

В
следующих книгах « Конических сечений»
Аполлоний рассматривает асимптоты
гиперболы, уравнение гиперболы
относительно этих асимптот, в частности,
уравнение равносторонней гиперболы в
виде
фокусы эллипса и гиперболы, число точек
пресечения двух конических сечений (
он доказывает, что число этих точек не
более четырех), ряд теорем о равенстве
площадей, связанных с коническими
сечениями, и др.

В
целом у него получается весьма полная,
объемистая, систематически изложенная
теория кривых второго порядка.

Конические
сечения Аполлония около двух тысяч лет
не находили применений в математическом
естествознаний и поэтому не получили
дальнейшего развития. Лишь в XVII
в. Кеплер установил, что все планеты
нашей солнечной системы движутся по
эллипсам, в одном из фокусов которых
находится Солнце, а Галилей выяснил,
что камень, брошенный под углом к
горизонту, летит в пустоте по параболе.
В том же XVII
в. Декарт и Ферма, а также их последователи,
пользуясь алгебраической символикой,
перевели основные понятия и ряд
предложений Аполлония на язык уравнений,
и тождеств и заложили основы аналитической
геометрии.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

У этого термина существуют и другие значения, см. Аполлоний.

Аполлоний Пергский
Дата рождения:	262 год до н. э.
Место рождения:	Перге, Памфилия
Дата смерти:	190 год до н. э.
Место смерти:	Александрия
Научная сфера:	геометрия

Аполло́ний Пергский (Ἀπολλώνιος ὁ Περγαῖος, Перге, 262 до н. э. — 190 до н. э.) — древнегреческий математик, один из трёх (наряду с Евклидом и Архимедом) великих геометров античности, живших в III веке до н. э.

Аполлоний прославился в первую очередь монографией «Конические сечения» (8 книг), в которой дал содержательную общую теорию эллипса, параболы и гиперболы. Именно Аполлоний предложил общепринятые названия этих кривых; до него их называли просто «сечениями конуса». Он ввёл и другие математические термины, латинские аналоги которых навсегда вошли в науку, в частности: асимптота, абсцисса, ордината, аппликата.

Из других заслуг Аполлония перед наукой отметим, что он переработал астрономическую модель Евдокса, введя эпициклы и эксцентрики для объяснения неравномерности движения планет. Эту теорию позднее развили Гиппарх и Птолемей. Он также дал решение задачи о построении окружности, касающейся трёх заданных окружностей («задача Аполлония»), изучал спиральные линии, занимался геометрической оптикой.

В честь Аполлония назван кратер на Луне.

Труд о конических сечениях

Четыре книги главного сочинения Аполлония о конических сечениях дошли до нас в греческом оригинале, три — в арабском переводе Сабита ибн Курры, а 8-я потеряна. Эдмонд Галлей подготовил образцовое издание данного труда (Оксфорд, 1710), куда включил свою попытку реконструкции VIII книги (на основании предисловия к VII книге). До Галлея аналогичную попытку предпринял Ибн ал-Хайсам.

Предшественниками Аполлония были Менехм, Конон Самосский, а также Евклид, чьё сочинение «Начала конических сечений» до нас не дошло. Евклид не включил теорию конических сечений в свои «Начала», вероятно, по той причине, что античные математики считали «совершенными линиями» только прямые и окружности.

В книге I приводятся определения и уравнения («симптомы») конических сечений — впрочем, известные и до Аполлония. Новым явилось то, что классификация кривых, как и в современных учебниках, проводится алгебраически — по виду уравнения, а не из геометрических соображений. Более того, Аполлоний строго доказывает, что вид уравнения не зависит от выбора опорной системы координат; в качестве таковой выступают, как правило, произвольный диаметр кривой и касательная в одном из концов диаметра, но Аполлоний рассматривает и другие косоугольные системы координат (например, для гиперболы — пара асимптот).

В последующем изложении (книги II—IV) выясняются свойства особых точек и линий, связанных с исследуемой кривой: фокусов, асимптот, полюсов и поляр, перечисляются их свойства, доказывается, что конические сечения могут пересекаться не более чем в 4 точках, поясняется, как строить касательные к этим кривым, определяются площади сегментов. Всего в труде 387 теорем.

В предисловии Аполлоний сообщает, что, начиная с III книги, бо́льшая часть теорем являются новыми.

V книга: теория нормалей и эволют для конических сечений, задачи на максимум и минимум.

VI книга: теория подобия конических сечений.

В VII-й (и, видимо, в VIII-й) книге приводятся знаменитые теоремы Аполлония о сопряжённых диаметрах и разнообразные приложения теории к геометрическим задачам.

Большой интерес представляют не только результаты Аполлония, но и методы, которыми он пользуется. В них можно найти многочисленные мотивы более поздних достижений математики — алгебры, аналитической, проективной геометрии и местами даже дифференциальной геометрии.

Книга оказала огромное влияние на творчество последующих математиков, включая Ферма, Декарта, Ньютона, Лагранжа и многих других. Многие теоремы Аполлония, особенно о максимумах, эволютах, нормалях и т. п. вошли в современные учебники по дифференциальной геометрии конических сечений.

Каким образом Аполлоний, не владея математическим анализом, сумел сделать свои открытия, неясно. Возможно, у него, как у Архимеда, был некий метод бесконечно малых, который он использовал в эвристических целях, чтобы затем передоказать результат каноническими средствами античной геометрии. Ван дер Варден пишет ^[1]:

Аполлоний виртуозно владеет геометрической алгеброй, но не менее виртуозно умеет скрывать свой первоначальный ход мыслей. Из-за этого-то его книгу и трудно понимать; рассуждения его элегантны и кристально ясны, но что его привело именно к таким рассуждениям, а не к иным каким-нибудь,— об этом можно лишь догадываться.

До открытий Кеплера и Ньютона теория Аполлония практически применялась в основном для решения кубических уравнений, а также в оптике зеркал. Когда обнаружилось, что орбита материальной частицы в задаче двух тел есть одно из конических сечений, интерес к данным кривым резко возрос, и труды Аполлония были продолжены на новом математическом уровне.

Другие труды Аполлония

В VII книге Математического собрания Паппа дается краткое описание шести математических трактатов Аполлония:

• Отсечение отношения (Λογου αποτομη) в двух книгах, содержащих 180 теорем. Рассматривается задача: даны две прямые и на каждой отмечено по точке; дана также третья точка, не совпадающая с первыми двумя, и требуется провести через неё прямую так, чтобы она отсекала на заданных прямых отрезки (считая от отмеченных точек), находящиеся в заданном отношении.
• Отсечение площади (Χωριου αποτομη) в двух книгах, содержащих 124 теоремы.
• Определенное сечение (Διωριςμενη τομη) в двух книгах, содержащих 83 теоремы.
• Вставки (Νευσεις) в двух книгах, содержащих 125 теорем.
• Касания (Επαφαι) в двух книгах, содержащих 60 теорем. В книге решается знаменитая проблема касания Аполлония: заданы три объекта, каждый из которых может быть точкой, прямой или окружностью. Требуется построить окружность, которая касается всех заданных объектов (для точки вместо касания требуется прохождение через неё).
• Плоские места (Τοποι επιπεδοι) в двух книгах, содержащих 147 теорем.

Из этих сочинений Аполлония сохранилось только первое — в средневековом арабском переводе. Папп написал также (частично дошедшие до нас) комментарии к этим трактатам.

В других трудах Папп упоминает ещё несколько сочинений Аполлония:

• Числа. Видимо, отклик на «Исчисление песчинок» Архимеда.
• О неупорядоченных иррациональностях. Комментарии Паппа к этому труду сохранились только в арабском переводе. Судя по ним, Аполлоний исследует классы иррациональных чисел, не рассмотренные в X книге Начал Евклида^[2].

Прокл Диадох в Комментарии к I книге Начал Евклида упоминает трактат Аполлония

• О Винтовых линиях (Περι του κοχλιου). Предположительно здесь рассматривались спирали на поверхности цилиндра^[2].

Так называемая XIV книга Начал Евклида, написанная Гипсиклом, представляет собой комментарий к сочинению Аполлония

• Сравнение додекаэдра с икосаэдром. Аполлоний доказывает, что поверхности додекаэдра и икосаэдра, вписанных в одну и ту же сферу, относятся так же, как их объёмы^[2].

Наконец, Евтокий в комментариях к Измерению круга Архимеда упоминает сочинение Аполлония

• Быстрое получение результатов (Ωκυτοκιον). Здесь Аполлоний соревнуется с Архимедом. Он описывает более удобную, чем у Архимеда, систему именования очень больших чисел, а также более быстрый, чем предложенный Архимедом, алгоритм вычисления отношения длины окружности к её диаметру.

Попытки восстановить утерянные сочинения по сохранившимся греческим и арабским упоминаниям предпринимали, кроме Галлея, также Виет (Касания^[3]), Ферма (Плоские места) и другие.

Древнегреческие авторы (например, Клавдий Птолемей в XII книге Альмагеста) упоминали открытия Аполлония в астрономии, однако ни одно его астрономическое сочинение не сохранилось.

Примечания

Литература

Тексты и переводы

Классические издания:

• 1710: Латинский перевод I—VII книг с греческого и арабского издал Эдмунд Галлей: Apollonii Pergaei Conicorum libri octo et Sereni Antissensis de Sectione Cylindri & Coni libri duo / Edidit Edmundus Halley. — Oxoniae: e Theatro Sheldoniano, 1710.
• 1891: I—IV книги на греческом, с латинским переводом, издал Иоганн Людвиг Гейберг: Apollonii Pergaei quae graece extant cum commentariis antiquiis / Ed. J. L. Heiberg.—Vol. 1—2.— Lipsiae: Teubner, 1891.
• PDF scans of Heiberg’s edition of Apollonius of Perga’s Conic Sections (греческий текст и английский перевод книг I—IV «Конических сечений»)
• 1990: V—VII книги на арабском, с английским переводом и комментариями издал Джералд Джеймс Тумер: Apollonius Conics Books V—VII. The Arabic translation of the lost Greek original / Edited with translation and commentary by G. J. Toomer.— Vol. 1-2. — NY a.o.: Springer, 1990.

Русский перевод отрывков:

• Аполлоний Пергский. Конические сечения, с комментариями Эвтокия / Пер. И.Ягодинского. Известия Северо-Кавказского гос. университета, 3(15), 1928, с. 130—152.

Исследования

• Барабанов О. О., Барабанова Л. П. Алгоритмы решения навигационной разностно-дальномерной задачи — от Аполлония до Коши // История науки и техники. — М., 2008. — № 11. — С. 2-21.
• Башмакова И. Г. Лекции по истории математики в Древней Греции // Историко-математические исследования. — М.: Физматгиз, 1958. — № 11. — С. 407-416.
• Ван дер Варден Б. Л. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. М.: Физматгиз, 1959.
• История математики с древнейших времён до начала XIX столетия (под ред. А. П. Юшкевича), том I, М., Наука, 1972.
• Лютер И. О. К истории задачи Аполлония о построении окружности, касающейся трёх данных окружностей. Историко-математические исследования, 1(36), № 2, 1996, с. 82-94.
• Розенфельд Б. А., Аполлоний Пергский, М.: МЦНМО, 2004.
• Хабелашвили А. В. Задача Аполлония Пергского. Историко-математические исследования, 1(36), часть 2, 1996, с. 66-81.
• Coolidge J.L. A history of the conic sections and quadric surfaces. Clarendon Press, Oxford, 1945. (Repr.: Dover, NY, 1968)
• Decorps-Foulquier M. Recherches sur les Coniques d’Apollonios de Pergé et leurs commentateurs grecs. Paris: Klincksieck, 2000.
• Federspiel M. Notes critiques sur le Livre I des Coniques d’Apollonius de Pergè. Revue des Études Grecques, 107, 1994, p. 203-218.
• Fried M. N. The use of analogy in Book VII of Apollonius’ Conica. Science in Context, 16, 2003, p. 349-365.
• Hogendiuk J. P. Arabic traces of lost works of Apollonius. Archive for History of Exact Sciences, 35, 1986, p. 187-253.
• Knorr W. R. The hiperbola-construction in the Conics, Book II: Ancient variations on a theorem of Apollonius. Centaurus, 25, 1982, p. 253-291.
• Neugebauer O. Studien zur Geschichte der antiken Algebra, II. Apollonius-Studien. Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik; B2, 1932, s. 215—254.
• Taisbak C. M. Discovering Apollonius’ circles. In: Proceedings of the Third International Conference on Ancient Mathematics, Delphi, 1996.
• Zeuthen H.G. Die Lehre vor den Kegelschnitten im Altertum. Copenhagen, 1886. (Repr.: Hildesheim, Georg Olms, 1966)

Ссылки

• Аполлоний Пергский // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
• Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. Аполлоний Пергский (англ.) в архиве MacTutor.

Александрийская школа
Наука	Александрийский Музей • Александрийская библиотека • Аполлоний Пергский • Аристарх Самосский • Аристилл • Герофил • Герон Александрийский • Евклид • Клавдий Птолемей • Конон Самосский • Никомед Александрийский • Тимохарис • Теон Александрийский • Эратосфен Киренский
Философия	Школа богословия: Афанасий Великий • Григорий Чудотворец • Дидим Слепой • Дионисий Александрийский • Иракл Александрийский • Кирилл Александрийский • Климент Александрийский • Ориген • Пантен • Пётр Александрийский • Филон Александрийский Школа неоплатонизма: Аммоний Гермий • Асклепий Тралльский • Гелиодор Александрийский • Гермий Александрийский • Гипатия • Давид Анахт • Иоанн Филопон • Немезий • Олимпиодор Младший • Синезий • Стефан Византийский • Эдесия
Филология	Аполлоний Эйдограф • Аристарх Самофракийский • Аристофан Византийский • Дидим Халкентер • Зенодот Эфесский • Эратосфен Киренский
Литература	Аполлоний Родосский • Арат • Каллимах • Ликофрон • Феокрит • Филит Косский

Математика в Древней Греции
Математики	Анаксагор · Анфимий · Архит · Аристей · Аристарх · Аполлоний · Архимед · Автолик · Бион · Боэций · Брайсон · Каллипп · Карп · Хрисипп · Клеомед · Конон · Ктезибий · Демокрит · Дикеарх · Диокл · Диофант · Динострат · Дионисодор · Домнин · Эратосфен · Евдем · Евклид · Евдокс · Евтокий · Гемин · Герон · Гиппарх · Гиппас · Гиппий · Гиппократ · Гипатия · Гипсикл · Исидор · Лев Математик · Марин · Мелисса · Менехм · Менелай · Метродор · Никомах · Никомед · Энопид · Папп · Персей · Филолай · Филон · Порфирий · Посидоний · Прокл · Птолемей · Пифагор · Серен · Симпликий · Созиген · Фалес · Теэтет · Феано · Феодор · Феодосий · Теон Александрийский · Теон Смирнский · Ксенократ · Зенон Элейский · Зенон Сидонский · Зенодор
Трактаты	Альмагест · Арифметика · Исчисление песчинок · Начала · О движущейся сфере · Палимпсест Архимеда · Труд о конических сечениях
Влияние	Вавилонская математика · Древнеегипетская математика
Под влиянием	Европейская математика · Индийская математика · Средневековая исламская математика
Таблицы	Список греческих математиков
Проблемы	Задача Аполлония · Квадратура круга · Трисекция угла · Удвоение куба

Древнегреческая астрономия
Астрономы	Акорей · Аглаоника · Агриппа · Анаксимандр · Андроник · Аполлоний · Арат из Сол · Аристарх · Аристилл · Атталий Родосский · Автолик · Бион · Каллипп · Клеомед · Клеострат Тенедосский · Конон Самосский · Эратосфен · Евктемон · Евдокс Книдский · Гемин · Гераклид Понтийский · Гикет · Гиппарх · Гиппократ Хиосский · Гипсикл · Менелай Александрийский · Метон Афинский · Энопид Хиосский · Филипп Опунтский · Филолай · Посидоний · Клавдий Птолемей · Пифей · Селевк · Созиген Александрийский · Созиген (перипатетик) · Страбон · Фалес Милетский · Феодосий · Теон Александрийский · Теон Смирнский · Тимохарис
Научные труды	Альмагест (Птолемей) · Антикитерский механизм · Армиллярная сфера · Астролябия · Диоптра · Экваториальный круг · Гномон · Квадрант · Трикветрум
Научные концепции	Цикл Каллиппа · Небесные сферы · Параллель · Противоземля · Эпицикл · Эквант · Геоцентрическая система мира · Гелиоцентрическая система мира · Цикл Гиппарха · Метонов цикл · Октетерис · Солнцестояние · Шарообразность Земли · Подлунная сфера · Зодиак
Связанные темы	Вавилонская астрономия · Астрономия Древнего Египта · Европейская астрономия · Индийская астрономия · Исламская астрономия

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Содержание

• биография
• Взносы
• Конические секции
• Классификация проблем
• Решение уравнений
• Теория эпицикла
• Сочинения
• 8 книг конических сечений
• О разделе причины
• Другие работы
• Ссылки 

Аполлоний Пергский (Перга, ок. 262 г. до н. Э. — Александрия, ок. 190 г. до н. Э.) Был математиком, геометром и астрономом из Александрийской школы, получившим признание за свою работу по конусам, важную работу, которая представляет собой значительный прогресс в астрономии. аэродинамика и другие области и науки, в которых она применяется. Его создание вдохновило других ученых, таких как Исаак Ньютон и Рене Декарт, на их более поздние технологические достижения в разное время.

Его работы Конические сечения родились эллипс, парабола и гипербола, термины и определения геометрических фигур, которые сегодня продолжают играть важную роль при решении математических задач.

Он также является автором гипотезы об эксцентрических орбитах, в которой он решает и детализирует предварительное движение планет и переменную скорость Луны. В своей теореме Аполлония он определяет, как две модели могут быть эквивалентными, если обе они начинаются с правильных параметров.

биография

Известный как «великий геометр», он родился примерно в 262 году до нашей эры. В Перге, расположенной в распавшейся Памфилии, во времена правления Птолемея III и Птолемея IV.

Он получил образование в Александрии как один из учеников Евклида. Он принадлежал к золотому веку математиков Древней Греции, основанному Аполлонием вместе с великими философами Евклидом и Архимедом.

Такие темы, как астрология, коники и схемы для выражения больших чисел характеризовали его исследования и основные работы.

Аполлоний был выдающейся фигурой в чистой математике. Его теории и результаты настолько опередили свое время, что многие из них были подтверждены лишь спустя долгое время.

И его мудрость была настолько сосредоточенной и скромной, что он сам утверждал в своих трудах, что теории следует изучать «для их же блага», как он заявил в предисловии к своей пятой книге Conics.

Взносы

Геометрический язык Аполлония считался современным. Следовательно, его теории и учения во многом сформировали то, что мы сегодня знаем как аналитическую геометрию.

Конические секции

Его самая важная работа — это Конические секции, который определяется как формы, полученные из конуса, пересекаемого разными плоскостями. Эти секции были разделены на семь: точка, линия, пара линий, парабола, эллипс, круг и гипербола.

Именно в этой книге он ввел термины и определения трех основных элементов геометрии: гиперболы, параболы и эллипса.

Он интерпретировал каждую из кривых, составляющих параболу, эллипс и гиперболу, как фундаментальное свойство коники, эквивалентное уравнению. Это, в свою очередь, применялось к наклонным осям, таким как оси, образованные диаметром и касательной на его конце, которые получаются путем разрезания наклонного кругового конуса.

Он показал, что наклонные оси — это просто особый вопрос, объяснив, что способ разрезания конуса не имеет значения и не имеет значения. Он доказал с помощью этой теории, что элементарное свойство конуса может быть выражено в самой форме, если оно основано на новом диаметре и касательной, расположенной на его конце.

Классификация проблем

Аполонио также классифицировал геометрические задачи на линейные, плоские и твердые в зависимости от их решения с кривыми, прямыми линиями, конусами и окружностями в зависимости от каждого случая. Это различие не существовало в то время и означало значительный прогресс, заложивший основы для выявления, организации и распространения их образования.

Решение уравнений

Используя новаторские геометрические методы, он предложил решение уравнений второй степени, которые до сих пор применяются в исследованиях в этой области и в математике.

Теория эпицикла

Эта теория была реализована в принципе Аполлонием Пергским, чтобы объяснить, как работает предполагаемое ретроградное движение планет в солнечной системе, концепция, известная как ретроградация, в которую вошли все планеты, кроме Луны и Солнца.

Он использовался для определения круговой орбиты, вокруг которой вращалась планета, с учетом местоположения ее центра вращения на другой дополнительной круговой орбите, на которой указанный центр вращения был смещен и где находилась Земля.

Теория устарела с более поздними достижениями Николая Коперника (гелиоцентрическая теория) и Иоганна Кеплера (эллиптические орбиты), среди других научных фактов.

Сочинения

До наших дней сохранились только две работы Аполлония: «Конические сечения» и «О разрезе разума». Его работы были разработаны в основном в трех областях, таких как геометрия, физика и астрономия.

8 книг конических сечений

Книга I: Методы получения и основные свойства коник.

Книга II: Диаметры, оси и асимптоты.

Книга III: Замечательные и новые теоремы. Свойства фонарей.

Книга IV: Число точек пересечения коник.

Книга V: Отрезки максимального и минимального расстояния до конусов. Нормальный, развивающийся, центр кривизны.

Книга VI: Равенство и подобие конических сечений. Обратная задача: по конусу найти конус.

Книга VII: Метрические отношения диаметров.

Книга VIII: ее содержание неизвестно, поскольку это одна из его потерянных книг. Существуют разные гипотезы о том, что на нем могло быть написано.

О разделе причины

Если есть две линии, и каждая из них имеет точку над ними, проблема состоит в том, чтобы провести другую линию через другую точку, чтобы при разрезании других линий потребовались сегменты, которые находятся в заданной пропорции. Сегменты — это отрезки длины, расположенные между точками на каждой из линий.

Это проблема, которую Аполлоний поднимает и решает в своей книге. О разделе причины.

Другие работы

О разделе области, Определенный раздел, Плоские места, Наклоны и касания или «проблема Аполонио» — другие из его многочисленных работ и вкладов, которые были потеряны во времени.

Великий математик Папо Александрийский был тем, кто в основном отвечал за распространение большого вклада и достижений Аполлония Пергского, комментировал его труды и распространял его важные работы в большом количестве книг.

Таким образом, из поколения в поколение работа Аполлония выходила за пределы Древней Греции и сегодня достигла Запада, будучи одной из наиболее представительных фигур в истории, установивших, охарактеризовавших, классифицирующих и определяющих природу математики и геометрии в мире. мир.

Ссылки 

1. Бойер, Карл П. История математики. Джон Вили и сыновья. Нью-Йорк, 1968 год.
2. Фрид, Майкл Н. и Сабетай Унгуру.Аполлоний Пергский Conica: текст, контекст, подтекст. Брилл, 2001.
3. Бертон, Д. М. История математики: Введение. (издание четвертое), 1999.
4. Гиш, Д. «Проблема Аполлония: исследование решений и их взаимосвязей», 2004.
5. Гринберг, М. Дж. Развитие и история евклидовой и неевклидовой геометрии. (Третье издание). W.H. Фримен и компания, 1993.

Аполлоний Пергский (262г. до н. э.- 190г. до н. э.), наряду с Евклидом и Архимедом традиционно входит в тройку «великих геометров античности», живших в III столетии до н. э.

Аполлоний Пергский родился в Перге (Малая Азия), получил образование в Александрии, где он жил ок. 210 г. до н. э. Умер ок. 190 г. до н. э. Жил и работал в Александрии, Пергаме и Эфесе. В математике он прославился выдающейся работой «Конические сечения» (8 книг), из которых сохранились только первые 4 книги и частично три последующие — в арабском переводе, сведения о восьмой и др. книгах сохранились в сочинениях более поздних античных авторов. Весь труд посвящен теории кривых второго порядка (эллипс, гипербола, парабола). Именно Аполлоний предложил классические названия данных кривых; до него их называли просто «сечениями конуса». Он ввёл и другие устоявшиеся математические термины, в частности: асимптота, абсцисса, ордината, аппликата. Любопытно, что он, как и современные математики, рассматривал обе ветви гиперболы как единую кривую.

Сохранилось ещё одно произведение Аполлония: «О сечении отношения», но только в арабском переводе. Другие его труды известны только по названиям, приведенным у Паппа.

Из других заслуг Аполлония перед наукой отметим, что именно он переработал астрономическую модель Евдокса, введя эпициклы и эксцентрики (для объяснения неравномерности движения планет). Гиппарх и Птолемей позже дополнили эту теорию, создав классическую геоцентрическую модель мира. Он также дал решение задачи о построении окружности, касающейся трех заданных окружностей («окружность Аполлония»), изучал спиральные линии, занимался геометрической оптикой.

В честь Аполлония назван кратер на Луне.

Сочинения Аполлония не влияли на развитие науки до VIII века. С появлением аналитической геометрии, механики и новой теории движения планет Кеплера наступило возрождение идей Аполлония. Таким образом, от создания теории Аполлония до ее применения на практике потребовалось 19 столетий.

Аполлоний Пергский (Греческий: Ἀπολλώνιος ὁ εργαῖος; латинский: Аполлоний Пергей; c. 240 г. до н.э. — c. 190 г. до н.э.) был Древнегреческий геометр и астроном известен своей работой над конические секции. Начиная с вкладов Евклид и Архимед по теме, он довел их до состояния до изобретения аналитическая геометрия. Его определения терминов эллипс, парабола, и гипербола те, которые используются сегодня.

Аполлоний работал над множеством других тем, включая астрономию. Большая часть этой работы не сохранилась, за исключением, как правило, фрагментов, на которые ссылаются другие авторы. Его гипотеза об эксцентрических орбитах для объяснения явно аберрантного движения планет, которая широко распространена до средневековья, была отвергнута в эпоху Возрождения.

Жизнь

Для такого важного сотрудника в области математики остается скудная биографическая информация. Греческий комментатор VI века, Евтокий из Аскалона, о главном произведении Аполлония, Коники, состояния:^[1]

«Аполлоний, геометрический … прибыл из Перги в Памфилии во времена Птолемея Эвергета, так пишет Гераклей, биограф Архимеда …»

Перга в то время был эллинизированным городом Памфилия в Анатолия. Руины города еще стоят. Это был центр эллинистической культуры. Эвергетес, «благодетель», определяет Птолемей III Эвергет, третья греческая династия Египта в преемственности диадохов. Предположительно, его «времена» — это его царствование, 246-222 / 221 гг. До н.э. Времена всегда записываются правителем или действующим судьей, так что, если бы Аполлоний родился раньше 246 г., это были бы «времена» отца Эвергета. Личность Гераклея неясна. Таким образом, приблизительные времена Аполлония известны, но точные даты не могут быть названы.^[2] Цифры «Удельные годы рождения и смерти», указанные различными учеными, являются лишь предположениями.^[3]

Евтокий, кажется, связывает Пергу с Династия птолемеев Египта. Никогда в Египте Перга в 246 г. до н. Э. Принадлежала Империя Селевкидов, независимый диадохи Государство управлялось династией Селевкидов. Во второй половине III века до нашей эры Перга несколько раз переходила из рук в руки, находясь то под властью Селевкидов, то под властью Селевкидов. Королевство Пергамон на север, управляемый Династия Атталидов. Можно было ожидать, что кто-то, названный «из Перги», жил и работал там. Напротив, если позже Аполлоний был отождествлен с Пергой, то не на основании его места жительства. Из оставшихся автобиографических материалов следует, что он жил, учился и писал в Александрии.

Письмо греческого математика и астронома Гипсикл Первоначально был частью приложения, взятого из Книги XIV Евклида, части тринадцати книг Элементов Евклида.^[4]

«Василид Тирский, O Протарх Когда он приехал в Александрию и познакомился с моим отцом, большую часть своего пребывания он провел с ним из-за их связи, возникшей из-за их общего интереса к математике. И однажды, когда заглянул в трактат Аполлония о сравнении додекаэдр и икосаэдр вписанные в одну и ту же сферу, то есть в вопросе о том, какое отношение они имеют друг к другу, они пришли к выводу, что трактовка этого Аполлонием в этой книге была неправильной; соответственно, как я понял от отца, они приступили к его исправлению и переписыванию. Но я сам впоследствии наткнулся на другую книгу, опубликованную Аполлонием, в которой демонстрировался рассматриваемый вопрос, и меня очень привлекло его исследование этой проблемы. Теперь книга, изданная Аполлонием, доступна всем; поскольку он имеет большой тираж в форме, которая, кажется, была результатом более поздней тщательной разработки ».« Со своей стороны, я решил посвятить вам то, что считаю необходимым, в качестве комментария, отчасти потому, что вы сможете по причине вашего мастерства во всей математике и особенно в геометрии, чтобы вынести экспертное суждение о том, что я собираюсь написать, и отчасти потому, что из-за вашей близости с моим отцом и вашего дружеского чувства ко мне вы окажете любезно выслушать мое исследование. Но пора закончить с преамбулой и начать сам трактат ».

Времена Аполлония

Аполлоний жил к концу исторического периода, который теперь называется Эллинистический период, характеризуемый наложением эллинской культуры на обширные неэллинские регионы на разную глубину, радикальным в одних местах, почти не в других. Изменение было инициировано Филипп II Македонский и его сын, Александр Великий, который, покорив всю Грецию череде ошеломляющих побед, отправился покорять Персидская империя, который управлял территориями от Египта до Пакистана. Филипп был убит в 336 г. до н. Э. Александр продолжил выполнение своего плана, завоевав обширную Персидскую империю.

Краткая автобиография Аполлония

Материал находится в уцелевших фальшивых «Предисловиях» к его книгам. Коники. Это письма, доставленные влиятельным друзьям Аполлония с просьбой просмотреть книгу, приложенную к письму. Предисловие к книге I, адресованное некоему Евдему, напоминает ему, что Коники первоначально был запрошен гостем дома в Александрии, геометром Навкратом, иначе неизвестным в истории. К концу визита у Навкрата был первый черновик всех восьми книг. Аполлоний называет их «без полного очищения» (оу диакатарантес по-гречески, ea non perpurgaremus на латыни). Он намеревался проверить и исправить книги, выпуская каждую по мере ее завершения.

Услышав об этом плане от самого Аполлония во время последующего визита последнего в Пергам, Евдем настоял на том, чтобы Аполлоний послал ему каждую книгу перед выпуском. Обстоятельства предполагают, что на этом этапе Аполлоний был молодым геометром, ищущим компанию и совет опытных профессионалов. Папп утверждает, что был со студентами Евклид в Александрии. Евклида давно не было. Это пребывание было, возможно, заключительным этапом обучения Аполлония. Евдем, возможно, был высокопоставленной фигурой в своем более раннем образовании в Пергаме; в любом случае есть основания полагать, что он был или стал руководителем Библиотечно-исследовательского центра (Музей ) Пергама. Аполлоний далее утверждает, что первые четыре книги были посвящены развитию элементов, а последние четыре касались специальных тем.

Между Предисловиями I и II есть некоторый пробел. Аполлоний послал своего сына, тоже Аполлония, доставить II. Он говорит с большей уверенностью, предлагая Евдемусу использовать книгу в специальных учебных группах, что подразумевает, что Евдемус был высокопоставленным лицом, если не директором, в исследовательском центре. Исследования в таких учреждениях, которые следовали модели Ликей из Аристотель в Афинах, из-за проживания Александр Великий и его товарищи в его северном отделении, были частью образовательной деятельности, к которой библиотека и музей были дополнением. В штате была всего одна такая школа. Принадлежащий королю, он находился под королевским патронажем, который, как правило, был ревнивым, восторженным и заинтересованным. Цари покупали, просили, одалживали и крали драгоценные книги всякий раз, когда и где могли. Книги были очень ценными, доступными только богатым читателям. Собирать их было королевской обязанностью. Пергамон был известен производством пергамента, поэтому «пергамент »Происходит от« Пергамон ».

Аполлоний напоминает Филонид Лаодикийский Геометра, которого он представил Евдему в Эфес. Филонид стал учеником Евдема. Он жил в основном в Сирии в первой половине II века до нашей эры. Указывает ли встреча, что Аполлоний теперь жил в Эфесе, не решено. Интеллектуальное сообщество Средиземноморья было интернациональным по культуре. Ученые были мобильны в поисках работы. Все они общались через какую-то почтовую службу, государственную или частную. Сохранившиеся письма в изобилии. Они навещали друг друга, читали работы друг друга, делали предложения друг другу, рекомендовали студентов и накопили традицию, которую некоторые называют «золотым веком математики».

Предисловие III отсутствует. Во время перерыва скончался Евдем, говорит Аполлоний в IV, снова подтверждая точку зрения, что Евдем был старше Аполлония. Предисловия IV – VII носят более формальный характер, они не содержат личной информации и сосредоточены на обобщении книг. Все они адресованы таинственному Атталу, выбор, сделанный «потому», как Аполлоний пишет Атталу, «из вашего искреннего желания владеть моими произведениями». К тому времени такое желание было у многих в Пергаме. Предположительно, этот Аттал был кем-то особенным, получившим копии шедевра Аполлония прямо из рук автора. Одна сильная теория состоит в том, что Атталус Attalus II Филадельфус, 220-138 гг. До н.э., генерал и защитник царства своего брата (Евмен II ), соправитель по болезни последнего в 160 г. до н. э. и наследник его престола и его вдова в 158 г. до н. э. Он и его брат были большими покровителями искусства, благодаря чему библиотека приобрела международное величие. Даты созвучны датам Филонида, тогда как мотив Аполлония созвучен инициативе Аттала по сбору книг.

Аполлоний послал Атталу Предисловия V – VII. В Предисловии VII он описывает Книгу VIII как «приложение» … «которое я постараюсь отправить вам как можно скорее». Нет никаких записей о том, что он был отправлен или когда-либо завершен. Он может отсутствовать в истории, потому что он никогда не был в истории, Аполлоний умер до его завершения. Папп Александрийский тем не менее, в нем есть леммы, так что по крайней мере какое-то его издание должно было когда-то находиться в обращении.

Документированные работы Аполлония

Аполлоний был плодовитым геометром, написавшим большое количество работ. Только один выживает, Коники. Это плотный и обширный справочник по теме, даже по сегодняшним меркам, служащий хранилищем малоизвестных сейчас геометрических утверждений, а также средством для некоторых новых, разработанных Аполлонием. Его аудиторией было не широкое население, которое не умело ни читать, ни писать. Он всегда предназначался для знатоков математики и их небольшого числа образованных читателей, связанных с государственными школами и связанными с ними библиотеками. Другими словами, это всегда был справочник по библиотеке.^[5] Его основные определения стали важным математическим наследием. По большей части ее методы и выводы были заменены Аналитической геометрией.

Из восьми его книг только первые четыре имеют правдоподобное заявление о происхождении от оригинальных текстов Аполлония. Книги 5-7 переведены с арабского на латынь. Оригинальный греческий язык был утерян. Статус Книги VIII неизвестен. Первый проект существовал. Был ли когда-либо выпущен окончательный вариант, неизвестно. Его «реконструкция» Эдмонда Галлея существует на латыни. Невозможно узнать, насколько оно похоже на Аполлония. Галлей также реконструировал De Rationis Sectione и De Spatii Sectione. Помимо этих работ, за исключением нескольких фрагментов, заканчивается документация, которую можно каким-либо образом интерпретировать как происходящую от Аполлония.

Многие из утерянных работ описаны или упомянуты комментаторами. Кроме того, есть идеи, приписываемые Аполлонию другими авторами без документации. Достоверно или нет, но это слухи. Некоторые авторы называют Аполлония автором определенных идей, впоследствии названных его именем. Другие пытаются выразить Аполлония в современной нотации или фразеологии с неопределенной степенью точности.

Коники

Греческий текст Коники использует евклидово расположение определений, фигур и их частей; то есть «данные», за которыми следуют предложения, «подлежащие доказательству». В книгах I-VII представлено 387 предложений. Такой тип расположения можно увидеть в любом современном учебнике геометрии традиционного предмета. Как и в любом курсе математики, материал очень плотный, и его рассмотрение обязательно медленное. У Аполлония был план для каждой книги, который частично описан в Предисловия. Заголовки, или указатели на план, в некоторой степени неполноценны, поскольку Аполлоний больше полагался на логическую последовательность тем.

Таким образом, для комментаторов веков создается интеллектуальная ниша. Каждый должен представить Аполлония наиболее ясным и актуальным для своего времени образом. Они используют множество методов: аннотации, обширный вводный материал, разные форматы, дополнительные рисунки, поверхностная реорганизация путем добавления capita и так далее. Есть тонкие вариации в интерпретации. Современный англоязычный человек сталкивается с нехваткой материала на английском языке из-за того, что английские ученые предпочитают новую латынь. Такие интеллектуальные английские гиганты, как Эдмунд Галлей и Исаак Ньютон, настоящие потомки эллинистической традиции математики и астрономии, могут быть прочитаны и интерпретированы в переводе только населением, говорящим по-английски, не знакомым с классическими языками; то есть большинство из них.

Презентации, полностью написанные на английском языке, начинаются в конце 19 века. Особо следует отметить Трактат о конических сечениях. Его обширный вводный комментарий включает в себя такие элементы, как словарь аполлонических геометрических терминов, дающих греческий язык, значения и использование.^[6] Комментируя, что «очевидно зловещая часть трактата удерживает многих от попыток познакомиться с ним»,^[7] он обещает добавить заголовки, внешне изменив организацию, и уточнить текст с помощью современных обозначений. Таким образом, в его работе упоминаются две системы организации, его собственная и система Аполлония, соответствие которым дано в скобках.

Работа Хита незаменима. Он преподавал на протяжении всего начала 20 века, скончавшись в 1940 году, но тем временем развивалась иная точка зрения. Колледж Святого Иоанна (Аннаполис / Санта-Фе), который был военным училищем с колониальных времен, до Военно-морская академия США в Аннаполис, Мэриленд, к которой он примыкает, в 1936 году лишился аккредитации и оказался на грани банкротства. В отчаянии правление вызвало Стрингфеллоу Барр и Скотт Бьюкенен от Чикагский университет, где разрабатывалась новая теоретическая программа обучения классике. Воспользовавшись возможностью, в 1937 году они учредили «новую программу» в Сент-Джонс, позже получившую название Великие книги программа, фиксированный учебный план, который будет обучать произведениям избранных ключевых участников культуры западной цивилизации. В монастыре Святого Иоанна Аполлония учили как самого себя, а не как какое-то дополнение к аналитическая геометрия.

«Наставником» Аполлония был Р. Кейтсби Талиаферро, новый доктор философии в 1937 г. Университет Вирджинии. Он был наставником до 1942 года, а затем в течение одного года, в 1948 году, сам предоставил английские переводы, перевел Птолемея. Альмагест и Аполлония Коники. Эти переводы стали частью Британской энциклопедии. Великие книги западного мира серии. Включены только книги I-III с приложением по специальным темам. В отличие от Хита, Талиаферро не пытался реорганизовать Аполлония, даже поверхностно, или переписать его. Его перевод на современный английский язык довольно точно следует греческому. Он до некоторой степени использует современные геометрические обозначения.

Одновременно с работой Талиаферро, Айвор Томас Оксфордский доктор эпохи Второй мировой войны проявлял большой интерес к греческой математике. Он спланировал сборник избранных материалов, который реализовался во время его военной службы в качестве офицера в армии. Королевский Норфолкский полк. После войны он нашел дом в Классическая библиотека Леба, где он занимает два тома, все переведенные Томасом, с греческим на одной стороне страницы и английским на другой, как это принято для серии Леба. Работа Томаса послужила руководством для золотого века греческой математики. Что касается Аполлония, он включает в основном только те части Книги I, которые определяют разделы.

Хит, Талиаферро и Томас удовлетворяли общественный спрос на Аполлония в переводе на протяжении большей части 20 века. Тема продолжается. Более поздние переводы и исследования включают новую информацию и точки зрения, а также исследуют старые.

Книга I

В книге I представлено 58 предложений. Его наиболее важным содержанием являются все основные определения конусов и конических сечений. Эти определения не совсем совпадают с современными определениями тех же слов. Этимологически современные слова происходят от древних, но этимон часто отличается по значению от своего рефлекс.

А коническая поверхность порождается отрезок повернулся около биссектриса точка так, чтобы конечные точки следовали круги, каждый по-своему самолет. А конус, одна из ветвей двойной конической поверхности, — это поверхность с точкой (вершина или же вершина ), круг (основание ), а ось — линия, соединяющая вершину и центр основания.

А “раздел »(Лат. Sectio, греческий фолиант) представляет собой воображаемое« разрезание »конуса самолет.

• Предложение I.3: «Если конус рассекается плоскостью через вершину, сечение будет треугольником». В случае двойного конуса сечение представляет собой два треугольника с углами при вершине вертикальные углы.
• Предложение I.4 утверждает, что сечения конуса, параллельные основанию, представляют собой окружности с центрами на оси.^[8]
• Предложение I.13 определяет эллипс, который понимается как разрезание единственного конуса плоскостью, наклоненной к плоскости основания и пересекающей последнюю по линии, перпендикулярной диаметру основания за пределами конуса (не показано). . Угол наклона плоскости должен быть больше нуля, иначе сечение будет окружностью. Он должен быть меньше соответствующего угла основания осевого треугольника, при котором фигура становится параболой.
• Предложение I.11 определяет параболу. Его плоскость параллельна стороне конической поверхности осевого треугольника.
• Предложение I.12 определяет гиперболу. Его плоскость параллельна оси. Он разрезал обе шишки пары, получив две отдельные ветви (показана только одна).

Греческие геометры были заинтересованы в размещении избранных фигур из своего инвентаря в различных приложениях инженерии и архитектуры, как это обычно делали великие изобретатели, такие как Архимед. Спрос на конические сечения был тогда и существует сейчас. Развитие математических характеристик продвинуло геометрию в направлении Греческая геометрическая алгебра, который наглядно демонстрирует такие основы алгебры, как присвоение значений линейным сегментам в качестве переменных. Они использовали систему координат, промежуточную между сеткой измерений и Декартова система координат. Теории пропорций и применения площадей позволили разработать визуальные уравнения. (См. Ниже в разделе «Методы Аполлония»).

«Применение областей» неявно спрашивает, учитывая площадь и линейный сегмент, применима ли эта область; то есть равен ли он квадрату на отрезке? Если да, применимость (парабола) установлена. Аполлоний вслед за Евклидом спросил, есть ли прямоугольник на абсцисса любой точки на сечении относится к квадрату ордината.^[9] Если это так, его слово-уравнение является эквивалентом что является одной из современных форм уравнения для парабола. У прямоугольника есть стороны и . Именно он соответственно назвал фигуру, параболу, «приложением».

Случай «неприменимости» далее делится на две возможности. Учитывая функцию, , так что в случае применимости , в случае неприменимости либо или же . В бывшем, отстает от величиной, называемой многоточием, «дефицит». В последнем случае превышения количества, называемого гиперболой, «избытком».

Применимость может быть достигнута путем добавления дефицита, , или вычитая излишек, . Фигура, компенсирующая дефицит, получила название эллипса; для избытка — гипербола.^[10] Члены современного уравнения зависят от перемещения и поворота фигуры от начала координат, но общее уравнение для эллипса,

Топор² + Автор² = C

можно поместить в форму

где C / B — это d, а уравнение гиперболы

Топор² — К² = C

становится

где C / B — s.^[11]

Книга II

Книга II содержит 53 предложения. Аполлоний говорит, что он намеревался охватить «свойства, имеющие отношение к диаметрам и осям, а также асимптоты и другие вещи … для пределов возможностей ». Его определение« диаметра »отличается от традиционного, поскольку он считает необходимым направить предполагаемого получателя письма к своей работе для определения. Упомянутые элементы — это те, которые указать форму и формирование фигур. Касательные рассматриваются в конце книги.

Книга III

Книга III содержит 56 предложений. Аполлоний заявляет об оригинальном открытии теорем «использования для построения твердых локусов … трехстрочных и четырехстрочных. локус …. «Геометрическое место конического сечения — это сечение. Задача о трехлинейном геометрическом месте (как указано в приложении Талиаферо к Книге III) находит« геометрическое место точек, расстояния которых от трех заданных фиксированных прямых … таковы что квадрат одного из расстояний всегда находится в постоянном соотношении к прямоугольнику, содержащемуся в двух других расстояниях ». Это доказательство применения площадей, образующих параболу.^[12] Задача с четырьмя линиями приводит к эллипсу и гиперболе. Аналитическая геометрия выводит одни и те же локусы из более простых критериев, поддерживаемых алгеброй, а не геометрией, за что Декарт получил высокую оценку. Он превосходит Аполлония в своих методах.

Книга IV

Книга IV содержит 57 предложений. Первый, посланный Атталу, а не Евдему, таким образом, представляет его более зрелую геометрическую мысль. Тема довольно специализированная: «наибольшее количество точек, в которых части конуса могут пересекаться друг с другом или пересекаться с окружностью круга…» Тем не менее, он говорит с энтузиазмом, называя их «весьма полезными». в решении проблем (Предисловие 4).^[13]

Книга V

Книга V, известная только благодаря переводу с арабского, содержит 77 предложений, больше, чем любая книга.^[14] Они покрывают эллипс (50 предложений), параболу (22) и гиперболу (28).^[15] Это не является явной темой, которая в Предисловиях I и V Аполлониус утверждает как максимальные и минимальные строки. Эти термины не поясняются. В отличие от Книги I, Книга V не содержит определений и объяснений.

Двусмысленность притягивает толкователей Аполлония, которые вынуждены толковать, не зная смысла основных терминов книги. До недавнего времени преобладала точка зрения Хита: линии следует рассматривать как нормали к сечениям.^[16] А нормальный в этом случае перпендикуляр к кривой на касательная точка иногда называют стопой. Если разрез построен в соответствии с системой координат Аполлония (см. Ниже в разделе «Методы Аполлония»), с диаметром (переведенным Хитом как ось) по оси x и вершиной в начале координат слева, фразеология предложения указывает, что минимумы / максимумы должны быть найдены между сечением и осью. Хит приходит к выводу о том, что неподвижная точка p на участке служит одновременно точкой касания и одним концом линии. Тогда минимальное расстояние между p и некоторой точкой g на оси должно быть нормалью от p.

В современной математике нормали к кривым известны тем, что являются местоположением центр кривизны той небольшой части кривой, расположенной вокруг стопы. Расстояние от ступни до центра — это радиус кривизны. Последний является радиус круга, но для других, кроме круговых кривых, малый дуга можно аппроксимировать дугой окружности. Кривизна некруглых кривых; например, конические участки должны меняться по сечению. Карта центра кривизны; то есть его место, когда ступня движется по секции, называется эволюционировать раздела. Такая фигура, край последовательных позиций линии, называется конверт сегодня. Хит полагал, что в Книге V мы видим, как Аполлоний устанавливает логическое основание теории нормалей, эволюций и конвертов.^[17]

Хитс считался авторитетной интерпретацией Книги V на протяжении всего 20 века, но изменение века повлекло за собой изменение взглядов. В 2001 году ученые Аполлония Фрид и Унгуру, отдавая должное другим главам Хита, возразили против историчности анализа Хита Книги V, заявив, что он «переработал оригинал, чтобы сделать его более подходящим для современного математика … такие вещи, которые делают работу Хита сомнительной ценностью для историка, раскрывая больше мыслей Хита, чем Аполлония ».^[18] Некоторые из его аргументов сводятся к следующему. Ни в предисловиях, ни в самих книгах нет упоминания о том, что максимумы / минимумы сами по себе являются нормами.^[19] Из 50 предложений Хита, которые, как утверждается, охватывают нормали, только 7, Книга V: 27-33, заявляют или подразумевают, что линии максимума / минимума перпендикулярны касательным. Эти 7 Фрид классифицирует как изолированные, не связанные с основными положениями книги. Они никоим образом не подразумевают, что максимумы / минимумы в целом являются нормальными. В своем обширном исследовании других 43 предложений Фрид доказывает, что многого быть не может.^[20]

Фрид и Унгуру противопоставляют его, изображая Аполлония как продолжение прошлого, а не предзнаменование будущего. Во-первых, это полное филологическое изучение всех ссылок на минимальные и максимальные строки, раскрывающее стандартную фразеологию.Есть три группы по 20-25 предложений в каждой.^[21] Первая группа содержит фразу «от точки на оси к сечению», которая является полной противоположностью гипотетической «от точки на сечении к оси». Первое не должно быть нормальным ни к чему, хотя может быть. Учитывая фиксированную точку на оси, из всех линий, соединяющих ее со всеми точками сечения, одна будет самой длинной (максимальной) и одной самой короткой (минимальной). Другие фразы: «в разрезе», «нарисовано из раздела», «отрезано между частью и его осью», отсечено по оси », и все они относятся к одному и тому же изображению.

По мнению Фрида и Унгуру, тема Книги V — это именно то, о чем говорит Аполлоний: строки максимума и минимума. Это не кодовые слова для будущих концепций, а относятся к использовавшимся тогда древним концепциям. Авторы цитируют Евклида, Элементы, Книгу III, которая касается кругов, а также максимальных и минимальных расстояний от внутренних точек до окружности.^[22] Не допуская какой-либо конкретной общности, они используют такие термины, как «подобное» или «аналог». Они известны тем, что вводят новый термин «подобный неусису». А конструкция Neusis был методом подгонки заданного сегмента между двумя заданными кривыми. Дана точка P и линейка с отмеченным на ней отрезком. один вращает линейку вокруг P, разрезая две кривые, пока сегмент не будет соответствовать между ними. В Книге V буква Р — точка на оси. Вращая вокруг него линейку, вы обнаруживаете расстояния до сечения, на которых можно различить минимум и максимум. Техника не применима к ситуации, так что это не невзирая. Авторы используют неусис-подобный, видя архетипическое сходство с древним методом.^[18]

Книга VI

Книга VI, известная только благодаря переводам с арабского, содержит 33 предложения — наименьшее из всех книг. Он также имеет большой лакуны, или пробелы в тексте из-за повреждения или искажения в предыдущих текстах.

Тема относительно ясная и бесспорная. В предисловии 1 говорится, что это «равные и похожие сечения конусов». Аполлоний расширяет концепции конгруэнтности и подобия, представленные Евклидом, на более элементарные фигуры, такие как треугольники, четырехугольники, на конические сечения. В предисловии 6 упоминаются «участки и сегменты», которые «равны и неравны», а также «похожи и непохожи», и добавляется некоторая конструктивная информация.

Книга VI имеет возврат к основным определениям в начале книги. «Равенство »Определяется приложением площадей. Если одна цифра; то есть раздел или сегмент «применяется» к другому (Галлея это приложение возможно альтера супер альтерам), они «равны» (Галлея aequales), если они совпадают и ни одна из линий одного не пересекает линию другого. Очевидно, это стандарт соответствие следуя Евклиду, Книга I, Общие понятия, 4: «и вещи совпадающие (эфармазанта) друг с другом равны (это). » Совпадение и равенство пересекаются, но это не одно и то же: применение площадей, используемых для определения разделов, зависит от количественного равенства площадей, но они могут принадлежать к разным фигурам.

Между экземплярами, которые являются одно и тоже (гомосексуалисты), равные друг другу, и те, которые разные, или же неравный, являются фигурами, которые являются «одинаковыми» (hom-oios), или похожий. Они не являются ни полностью одинаковыми, ни разными, но имеют общие аспекты и не имеют общих аспектов, которые являются разными. Интуитивно геологи шкала в уме; например, карта похожа на топографический регион. Таким образом, фигуры могут иметь более крупную или меньшую версию самих себя.

Аспекты, которые совпадают на подобных рисунках, зависят от рисунка. В 6-й книге «Элементов» Евклида представлены треугольники, похожие на те, которые имеют такие же соответствующие углы. Таким образом, треугольник может иметь сколь угодно маленькие миниатюры или гигантские версии, и при этом быть «таким же» треугольником, что и оригинал.

В определениях Аполлония в начале книги VI подобные правые конусы имеют аналогичные осевые треугольники. Подобные участки и отрезки участков находятся прежде всего в одинаковых конусах. Кроме того, для каждой абсциссы одного должна существовать абсцисса другого в желаемом масштабе. Наконец, абсцисса и ордината одного должны совпадать с координатами того же отношения ординаты к абсциссе, что и у другого. Общий эффект такой, как если бы секция или сегмент перемещались вверх и вниз по конусу для достижения другого масштаба.^[23]

Книга VII

Книга VII, также перевод с арабского, содержит 51 предложение. Это последнее, что Хит рассматривает в своем издании 1896 года. В Предисловии I Аполлоний не упоминает о них, подразумевая, что на момент написания первого наброска они, возможно, не существовали в достаточно связной форме для описания. Аполлоний использует непонятный язык, говоря, что это «peri dioristikon Theorematon», что Галлей перевел как «de Theorematis ad definitionem pertinentibus», а Хит — как «теоремы, включающие определения пределов». Это язык определений, но никаких определений не предлагается. Вопрос о том, может ли ссылка относиться к определенному виду определений, является предметом рассмотрения, но на сегодняшний день не предложено ничего достоверного.^[24] Тема Книги VII, завершенная к концу жизни и карьеры Аполлония, изложена в Предисловии VII как диаметры и «изображенные на них рисунки», которые должны включать сопряженные диаметры, поскольку он в значительной степени полагается на них. Каким образом могут применяться термины «пределы» или «определения», не упоминается.

Диаметры и их сопряжения определены в Книге I (Определения 4-6). Не каждый диаметр имеет сопряжение. Топография диаметра (греческий диаметр) требует регулярного изогнутый фигура. Области неправильной формы, к которым обращаются в наше время, не входили в древний план игры. Аполлоний, конечно, имеет в виду конические сечения, которые он часто описывает запутанным языком: «кривая в одной плоскости» — это круг, эллипс или парабола, а «две кривые в одной плоскости» — это гипербола. А аккорд — прямая, две конечные точки которой находятся на фигуре; то есть разрезает фигуру в двух местах. Если на фигуру наложена сетка из параллельных хорд, то диаметр определяется как линия, разделяющая все хорды пополам и достигающая самой кривой в точке, называемой вершиной. Нет необходимости в закрытой фигуре; например, парабола имеет диаметр.

Парабола имеет симметрия в одном измерении. Если представить, что он сложен на один диаметр, две половинки совпадают или подходят друг к другу. То же самое можно сказать об одной ветви гиперболы. Сопряженные диаметры (греч. Suzugeis diametroi, где suzugeis «связаны вместе»), однако, симметричны в двух измерениях. Цифры, к которым они относятся, требуют также ареального центра (греч. Kentron), который сегодня называется центроид, служащий центром симметрии в двух направлениях. Эти фигуры представляют собой круг, эллипс и двуветвленную гиперболу. Есть только один центроид, который не следует путать с фокусы. Диаметр — это хорда, проходящая через центр тяжести, который всегда делит его пополам.

Для круга и эллипса пусть сетка параллельных хорд будет наложена на фигуру так, чтобы самая длинная из них была диаметром, а другие последовательно короче, пока последняя не стала хордой, а стала точкой касания. Касательная должна быть параллельна диаметру. Сопряженный диаметр делит хорды пополам и помещается между центроидом и точкой касания. Более того, оба диаметра сопряжены друг с другом и называются сопряженной парой. Очевидно, что любые сопряженные пары окружности перпендикулярны друг другу, но в эллипсе только большая и малая оси, а удлинение разрушает перпендикулярность во всех остальных случаях.

Конъюгаты определены для двух ветвей гипербола в результате разрезания двойного конуса одной плоскостью. Их называют сопряженными ветвями. У них одинаковый диаметр. Его центроид делит пополам отрезок между вершинами. Есть место для еще одной диаметральной линии: пусть сетка из линий, параллельных диаметру, разрезает обе ветви гиперболы. Эти линии похожи на хорды, за исключением того, что они не заканчиваются на одной и той же непрерывной кривой. Сопряженный диаметр может быть проведен от центра тяжести, чтобы разделить хорды пополам.

Эти концепции в основном из Книги I позволяют нам начать с 51 предложения Книги VII, детально определяющего отношения между сечениями, диаметрами и сопряженными диаметрами. Как и в случае с некоторыми другими специализированными темами Аполлония, их полезность сегодня по сравнению с Аналитической геометрией еще предстоит увидеть, хотя он утверждает в Предисловии VII, что они одновременно полезны и новаторски; то есть он берет на себя заслугу перед ними.

Утраченные и восстановленные произведения, описанные Паппом

Папп упоминает и другие трактаты Аполлония:

1. Λόγου ἀποτομή, De Rationis Sectione («Сокращение соотношения»)
2. Χωρίου ἀποτομή, De Spatii Sectione («Вырезание участка»)
3. Διωρισμένη τομή, De Sectione Determinata («Определенный раздел»)
4. Ἐπαφαί, De Tactionibus («Касания»)^[25]
5. Νεύσεις, De Inclinationibus («Наклоны»)
6. Τόποι ἐπίπεδοι, De Locis Planis («Плоские места»).

Каждая из них была разделена на две книги, и — с Данные, то Поризмы, и Поверхность-локусы Евклида и Коники Аполлония — были, по Паппу, включены в основу античного анализа.^[12] Далее следуют описания шести упомянутых выше работ.

De Rationis Sectione

De Rationis Sectione стремился решить простую проблему: даны две прямые и точка в каждой, проведите через третью заданную точку прямую линию, пересекающую две фиксированные линии так, чтобы части пересекались между заданными точками в них и точками пересечения с этой третьей линия может иметь заданное соотношение.^[12]

De Spatii Sectione

De Spatii Sectione обсудили аналогичную проблему, требующую, чтобы прямоугольник, содержащийся в двух перехватчиках, был равен заданному прямоугольнику.^[12]

В конце 17 века Эдвард Бернард обнаружил версию De Rationis Sectione в Библиотека имени Бодлея. Хотя он начал перевод, именно Галлей закончил его и включил в том 1706 года с его реставрацией. De Spatii Sectione.

De Sectione Determinata

De Sectione Determinata рассматривает проблемы способом, который можно назвать аналитической геометрией одного измерения; с вопросом о нахождении точек на линии, которые были в соотношении с другими.^[26] Конкретные проблемы заключаются в следующем: даны две, три или четыре точки на прямой, найдите другую точку на ней так, чтобы ее расстояния от данных точек удовлетворяли условию, что квадрат на одной или прямоугольник, содержащий два, имеет заданное соотношение либо ( 1) к квадрату на оставшейся одной или к прямоугольнику, содержащемуся в оставшихся двух, или (2) к прямоугольнику, содержащемуся в оставшейся одной и другой заданной прямой. Некоторые пытались восстановить текст, чтобы найти решение Аполлония, среди них Снеллий (Виллеброрд Снелл, Лейден, 1698); Александр Андерсон из Абердин, в приложении к его Аполлоний Редививус (Париж, 1612 г.); и Роберт Симсон в его Опера quaedam reliqua (Глазго, 1776 г.), безусловно, лучшая попытка.^[12]

De Tactionibus

Для получения дополнительной информации см. Проблема Аполлония.

De Tactionibus охватил следующую общую задачу: для заданных трех объектов (точек, прямых линий или окружностей) в позиции описать круг, проходящий через заданные точки и касающийся заданных прямых линий или окружностей. Самый сложный и исторически интересный случай возникает, когда эти три данные представляют собой круги. В 16 веке Виета представил эту проблему (иногда известную как проблема Аполлонии) Адриан Романус, который решил это с помощью гипербола. Виета предложил более простое решение, что в конечном итоге привело его к восстановлению всего трактата Аполлония в небольшом труде. Аполлоний Галл (Париж, 1600). История проблемы подробно рассматривается в предисловии к Дж. В. Камерер кратко Apollonii Pergaei quae supersunt, ac maxime Lemmata Pappi in hos Libras, cum Observationibus и т. Д. (Гота, 1795, 8vo).^[12]

De Inclinationibus

Объект De Inclinationibus должен был продемонстрировать, как прямая линия заданной длины, стремящаяся к заданной точке, может быть вставлена ​​между двумя заданными (прямыми или круговыми) линиями. Хотя Марин Гетальдич и Hugo d’Omerique (Геометрический анализ, Кадис, 1698) попытки реставрации, лучшая работа Самуэля Хорсли (1770).^[12]

De Locis Planis

De Locis Planis представляет собой набор предложений, относящихся к локусам, которые являются прямыми линиями или кругами. Поскольку Папп дает несколько полные подробности своих предложений, этот текст также видел попытки восстановить его, не только П. Ферма (Oeuvres, i., 1891, pp. 3–51) и F. Schooten (Лейден, 1656 г.), но наиболее удачно — Р. Симсон (Глазго, 1749 г.).^[12]

Утраченные произведения, упомянутые другими древними писателями

Древние писатели ссылаются на другие произведения Аполлония, которые более не сохранились:

1. Περὶ τοῦ πυρίου, На горящем стекле, трактат, вероятно, исследующий фокусные свойства параболы
2. Περὶ τοῦ κοχλίου, На цилиндрической спирали (упоминается Проклом)
3. Сравнение додекаэдра и икосаэдра, вписанных в одну сферу
4. Ἡ καθόλου πραγματεία, работа по общим принципам математики, которая, возможно, включала критику Аполлония и предложения по улучшению Евклидова Элементы
5. Ὠκυτόκιον («Быстрое зачатие»), в котором, согласно Евтокию, Аполлоний продемонстрировал, как найти более близкие пределы ценности π чем у Архимед, кто рассчитал3 ¹⁄₇ как верхний предел и3 ¹⁰⁄₇₁ как нижний предел
6. арифметическое произведение (см. Паппус ) в системе как для выражения больших чисел на языке более повседневном, чем у Архимеда. Счетчик песка и для умножения этих больших чисел
7. великое расширение теории иррациональных чисел, изложенное в Евклиде, Книга x., от биномиального к полиномиальному и от упорядоченный к неупорядоченный иррациональные (см. отрывки из сообщения Паппа о Евкл. x., сохраненные на арабском языке и опубликованные Woepke, 1856).^[12]

Ранние печатные издания

Первопечатные издания начались в основном в 16 веке. В то время ожидалось, что научные книги будут на латыни, а сегодня Новая латынь. Поскольку рукописей на латыни почти не было, редакторы старопечатных произведений переводили с греческого или арабского на латынь. Греческий и латинский языки обычно сопоставляли, но только греческий является оригинальным, иначе редактор восстановил то, что он считал оригиналом. Критические аппараты были на латыни. Однако древние комментарии были на древнегреческом или средневековом. Только в 18-19 веках начали появляться современные языки. Ниже приводится репрезентативный список старопечатных изданий. Оригиналы этих репродукций редки и дороги. Для современных изданий на современных языках смотрите ссылки.

1. Пергей, Аполлоний (1566 г.). Conicorum libri quattuor: una cum Pappi Alexandrini lemmatibus, et commentariis Eutocii Ascalonitae. Sereni Antinensis Философская библиотека duo … quae omnia nuper Federicus Commandinus Vrbinas mendis quampluris expurgata e Graeco conuertit, & commentariis illustrauit (на древнегреческом и латинском). Bononiae: Ex officina Alexandri Benatii. Презентация первых четырех книг Коники на греческом Фредерик Коммандинус с собственным переводом на латынь и комментариями Папп Александрийский, Евтокий из Аскалона и Серен Антиноплисский.
2. Аполлоний; Барроу, я (1675). Apollonii conica: Methodo nova illustrata и succinctè manifestrata (на латыни). Londini: Excudebat Guil. Godbid, voeneunt apud Robertum Scott, in vico Little Britain. Перевод Барроу с древнегреческого на неолатинский язык первых четырех книг Коники. Ссылка здесь, находится в Бостонская публичная библиотека, когда-то принадлежал Джон Адамс.
3. Аполлоний; Паппус; Галлей, Э. (1706). Apollonii Pergaei de sectione rationis libri duo: Ex Arabico ms. Латинская версия. Accedunt ejusdem de sectione spatii libri duo restituti (на латыни). Oxonii. Презентация двух утраченных, но восстановленных произведений Аполлония. De Sectione Rationis происходит из неопубликованной рукописи на арабском языке в Библиотека имени Бодлея в Оксфорде, первоначально частично переведенный Эдвард Бернард но прервано его смертью. Это было дано Эдмонд Галлей, профессор, астроном, математик и исследователь, в честь которого Комета Галлея позже был назван. Не сумев расшифровать искаженный текст, он отказался от него. Впоследствии Дэвид Грегори (математик) восстановил арабский для Генри Олдрич, который снова отдал его Галлею. Изучая арабский язык, Галлей создал De Sectione Rationis и в качестве дополнительного вознаграждения для читателя создал неолатинский перевод версии De Sectione Spatii реконструирован из комментария Паппа к нему. Два неолатинских сочинения и древнегреческий комментарий Паппа были объединены в единый том 1706 года. Автор арабской рукописи не известен. На основании заявления, что он был написан «под эгидой» Аль-Мамун По латинскому алфавиту Алмамон, астроном и халиф Багдада в 825 г., Галлей датирует его 820 г. в своем «Praefatio ad Lectorem».
4. Аполлоний; Александринус Папп; Галлей, Эдмонд; Евтокий; Серен (1710). Apollonii Pergaei Conicorum libri octo, et Sereni Antissensis De sectione cylindri & coni libri duo (PDF) (на латыни и древнегреческом). Oxoniae: e Theatro Sheldoniano. Ободренный успехом своего перевода исправленного арабского текста Давида Грегори de Sectione rationis, опубликованный в 1706 году, Галлей восстановил и перевел на латынь всю книгу Аполлония. elementa conica.^[27] Книги I-IV никогда не терялись. Они появляются с греческим в одном столбце и латынью Галлея в параллельном столбце. Книги V-VI появились в результате неожиданного открытия ранее недооцененного перевода с греческого на арабский, купленного ученым-антикваром. Якобус Голиус в Алеппо в 1626 году. После его смерти в 1696 году он перешел цепочкой покупок и завещаний в Бодлианскую библиотеку (первоначально как MS Marsh 607, датированная 1070 годом).^[28] Перевод, датированный гораздо более ранним временем, взят из филиала школы Алмамона под названием Бану Муса, «Сыновья Мусы», группа из трех братьев, живших в 9 веке. Перевод выполнен работающими для них писателями.^[3] В работе Галлея дан только латинский перевод Книг V-VII. Это его первое печатное издание. Книга VIII была утеряна прежде, чем ученые Алмамона смогли приложить руку к ее сохранению. Выдумка Галлея, основанная на ожиданиях, изложенных в книге VII, и леммах Паппа, дана на латыни. Комментарий Евтокия, леммы Паппа и два связанных трактата Серена включены в качестве руководства к интерпретации Коники.

Идеи, приписываемые Аполлонию другими писателями

Вклад Аполлония в астрономию

Эквивалентность двух описаний движений планет, одно с использованием эксцентриков, а другое деферент и эпициклы, приписывается ему. Птолемей описывает эту эквивалентность как Теорема Аполлония в Альмагест XII.1.

Методы Аполлония

По словам Хита,^[29] «Методы Аполлония» не были его и не были личными. Какое бы влияние он ни оказал на более поздних теоретиков, было влияние геометрии, а не его собственного новаторства в технике. Хит говорит:

«В качестве предварительного к подробному рассмотрению методов, используемых в кониках, можно в целом заявить, что они неуклонно следуют принятым принципам геометрического исследования, которые нашли свое окончательное выражение в элементах Евклида».

Что касается современных людей, говорящих о геометрах золотого века, термин «метод» означает, в частности, визуальный, реконструктивный способ, которым геометр неосознанно дает тот же результат, что и алгебраический метод, используемый сегодня. В качестве простого примера алгебра находит площадь квадрата, возводя его в квадрат. Геометрический метод достижения того же результата — построение визуального квадрата. Геометрические методы в золотой век могли дать большинство результатов элементарной алгебры.

Геометрическая алгебра

Хит продолжает использовать термин геометрическая алгебра для методов всего золотого века. По его словам, этот термин назван «правильно». Сегодня этот термин воскрес для использования в других смыслах (см. геометрическая алгебра ). Хит использовал это, как это было определено Генри Берчард Файн в 1890 году или раньше.^[30] Прекрасно относится к La Géométrie из Рене Декарт, первая полноценная работа аналитическая геометрия. Устанавливая в качестве предварительного условия, что «две алгебры формально идентичны, фундаментальные операции которых формально одинаковы», Файн говорит, что работа Декарта «не … просто числовая алгебра, но то, что из-за отсутствия лучшего названия может быть названо алгеброй отрезки линии. Его символика такая же, как и у числовой алгебры; …. »

Например, у Аполлония отрезок AB (линия между точками A и B) также является числовой длиной отрезка. Он может иметь любую длину. Таким образом, AB становится тем же, что и алгебраическая переменная, Такие как Икс (неизвестное), которому может быть присвоено любое значение; например., Икс=3.

Переменные определяются в Аполлонии с помощью таких словосочетаний, как «пусть AB будет расстоянием от любой точки на сечении до диаметра» — практика, которая продолжается в алгебре сегодня. Каждый студент, изучающий основы алгебры, должен научиться преобразовывать «словесные задачи» в алгебраические переменные и уравнения, к которым применяются правила алгебры при решении Икс. У Аполлония таких правил не было. Его решения геометрические.

Отношения, которые не поддались живописным решениям, были ему недоступны; тем не менее, его репертуар живописных решений возник из пула сложных геометрических решений, которые сегодня обычно не известны (или не требуются). Одно известное исключение — незаменимое Теорема Пифагора, даже сейчас представленный прямоугольным треугольником с квадратами по бокам, иллюстрирующими такое выражение, как² + b² = c². Греческие геометры называли эти термины «квадратом на AB» и т. Д. Точно так же площадь прямоугольника, образованного AB и CD, была «прямоугольником на AB и CD».

Эти концепции дали греческим геометрам алгебраический доступ к линейные функции и квадратичные функции, которыми являются конические сечения. В них содержатся полномочия 1 или 2 соответственно. Аполлоний не особо любил кубики (показанные в сплошная геометрия ), хотя конус — твердое тело. Его интересовали конические сечения, которые представляют собой плоские фигуры. Степени 4 и выше были недоступны для визуализации, требуя некоторой степени абстракции, недоступной в геометрии, но готовой в алгебре.

Система координат Аполлония

Все обычные измерения длины в общественных единицах, таких как дюймы, с использованием стандартных общедоступных устройств, таких как линейка, подразумевают общественное признание Декартова сетка; то есть поверхность, разделенная на единичные квадраты, например один квадратный дюйм, и пространство, разделенное на единичные кубы, например, один кубический дюйм. В древнегреческие единицы измерения предоставил такую ​​сетку греческим математикам с бронзового века. До Аполлония Менахм и Архимед уже начали размещать свои фигуры в подразумеваемом окне общей сетки, ссылаясь на расстояния, которые, как предполагалось, должны измеряться от левой вертикальной линии, обозначающей нижнюю меру, и нижней горизонтальной линии, обозначающей нижнюю меру, направления являются прямолинейными или перпендикулярными для другого.^[31] Эти края окна становятся в Декартова система координат, топоры. Один определяет прямолинейные расстояния любой точки от осей как координаты. У древних греков такой договоренности не было. Они просто ссылались на расстояния.

У Аполлония действительно есть стандартное окно, в которое он помещает свои фигуры. Вертикальное измерение происходит от горизонтальной линии, которую он называет «диаметром». В греческом это слово такое же, как и в английском, но греческий язык несколько шире в своем понимании.^[32] Если фигура конического сечения разрезана сеткой параллельных линий, диаметр делит пополам все линейные сегменты, включенные между ветвями фигуры. Он должен проходить через макушку (коруфе, «корона»). Таким образом, диаметр состоит из открытых фигур, таких как парабола, а также замкнутых фигур, таких как круг. Нет никаких указаний на то, что диаметр должен быть перпендикулярен параллельным линиям, но Аполлоний использует только прямолинейные.

Прямолинейное расстояние от точки на сечении до диаметра на греческом языке называется тетагменос, этимологически просто «протяженный». Поскольку это слово всегда расширяется только «вниз» (ката-) или «вверх» (ана-), переводчики интерпретируют его как ордината. В этом случае диаметр становится осью x, а вершина — началом координат. Затем ось y становится касательной к кривой в вершине. В абсцисса затем определяется как отрезок диаметра между ординатой и вершиной.

Используя свою версию системы координат, Аполлонию удается разработать в наглядной форме геометрические эквиваленты уравнений для конических сечений, что поднимает вопрос о том, можно ли считать его систему координат декартовой. Есть некоторые отличия. Декартова система должна рассматриваться как универсальная, охватывающая все цифры во всем пространстве до того, как будут выполнены какие-либо вычисления. Он состоит из четырех квадрантов, разделенных двумя скрещенными осями. Три квадранта включают отрицательные координаты, означающие направления, противоположные исходным осям нуля.

Аполлоний не имеет отрицательных чисел, не имеет явно числа, равного нулю, и не развивает систему координат независимо от конических сечений. Он работает по существу только в квадранте 1, все положительные координаты. Карл Бойер, современный историк математики, говорит:^[33]

Однако греческая геометрическая алгебра не предусматривала отрицательных величин; кроме того, система координат в каждом случае накладывалась апостериорный на заданной кривой, чтобы изучить ее свойства … Аполлоний, величайший геометр древности, не смог разработать аналитическую геометрию … «»

Однако никто не отрицает, что Аполлоний занимает своего рода промежуточную нишу между сеточной системой традиционных измерений и полностью разработанной декартовой системой координат аналитической геометрии. Читая Аполлония, нужно стараться не принимать его термины в современном значении.

Теория пропорций

Аполлоний использует «Теорию пропорций», выраженную в Евклид С Элементы, Книги 5 и 6. Эта теория, разработанная Евдоксом Книдским, занимает промежуточное положение между чисто графическими методами и современной теорией чисел. Отсутствует стандартная десятичная система счисления, как и стандартная обработка дробей. Утверждения, однако, выражают на словах правила манипулирования дробями в арифметике. Хит предлагает заменить их умножением и делением.^[34]

Под термином «величина» Евдокс надеялся выйти за рамки чисел и перейти к общему пониманию размера, значение, которое он сохраняет до сих пор. Что касается фигур Евклида, это чаще всего означает числа, что и было подходом Пифагора. Пифагор считал, что Вселенная может быть охарактеризована количествами, что стало современной научной догмой. Книга V Евклида начинается с утверждения, что величина (мегетос, «размер») должна делиться поровну на единицы (мерос, «часть»). Таким образом, величина кратна единицам. Они не обязательно должны быть стандартными единицами измерения, такими как метры или футы. Один блок может быть любым обозначенным отрезком линии.

Далее следует, пожалуй, самое полезное фундаментальное определение, когда-либо придуманное в науке: соотношение (греч. логотипы, что примерно означает «объяснение») — это утверждение относительной величины. Даны две величины, скажем, отрезков AB и CD. отношение AB к CD, где CD считается единицей, является количеством CD в AB; например, 3 части 4 или 60 частей на миллион, где промилле по-прежнему использует терминологию «частей». Отношение является основой современной дроби, которая также по-прежнему означает «часть» или «фрагмент» от того же латинского корня, что и дробь. Отношение является основой математического предсказания в логической структуре, называемой «пропорцией» (греч. аналоги). Пропорция утверждает, что если два сегмента, AB и CD, имеют такое же соотношение, как два других, EF и GH, тогда AB и CD пропорциональны EF и GH, или, как было бы сказано в Евклиде, AB относится к CD как EF. для GH.

Алгебра сводит это общее понятие к выражению AB / CD = EF / GH. Учитывая любые три члена, можно вычислить четвертое как неизвестное. Преобразуя приведенное выше уравнение, получаем AB = (CD / GH) • EF, в котором, выраженное как y = kx, CD / GH известно как «константа пропорциональности». Грекам было несложно брать кратные (греч. Pollaplasiein), вероятно, путем последовательного сложения.

Аполлоний использует соотношения почти исключительно линейных сегментов и площадей, обозначенных квадратами и прямоугольниками. Переводчики обязались использовать двоеточие, введенное Готфрид Вильгельм Лейбниц в Acta Eruditorum, 1684.^[35] Вот пример из Коники, Книга I, по предложению 11:

Дословный перевод греческого: пусть будет надумано, что (квадрат) BC соответствует (прямоугольнику) BAC, как FH — FA.

Перевод Талиаферро: «Пусть будет надуманным, что кв. BC: rect. BA.AC :: FH: FA »

Алгебраический эквивалент: BC²/ BA • BC = FH / FA

Почести, оказанные историей

Кратер Аполлоний на Луна назван в его честь.

Смотрите также

Примечания

Рекомендации

• Альхазен; Хогендейк, JP (1985). Завершение Ибн аль-Хайсама «Коников». Нью-Йорк: Springer Verlag.
• Аполлоний Пергский; Галлей, Эдмунд; Бальзам, Пауль Генрих (1861). Des Apollonius von Perga sieben Bücher über Kegelschnitte Nebst dem durch Halley wieder hergestellten achten Buche; dabei ein Anhang, энтузиазм Die auf die Geometrie der Kegelschnitte bezüglichen Sätze aus Ньютон «Натуральные принципы математики». (на немецком). Берлин: Де Грюйтер.
• В эту статью включен текст из публикации, которая сейчас находится в всеобщее достояние: Хит, Томас Литтл (1911). «Аполлоний Пергский «В Чисхолме, Хью (ред.)». Британская энциклопедия. 2 (11-е изд.). Издательство Кембриджского университета. С. 186–188.
• Аполлоний Пергский; Галлей, Эдмунд; Фрид, Майкл Н (2011). Реконструкция Эдмонда Галлея утерянной книги Коников Аполлония: перевод и комментарии. Источники и исследования по истории математики и физических наук. Нью-Йорк: Спрингер. ISBN  978-1461401452.
• Аполлоний Пергский; Хит, Томас Литтл (1896). Трактат о конических сечениях. Кембридж: Издательство университета.
• Аполлоний Пергский; Heiberg, JL (1891). Apollonii Pergaei quae Graece exstant cum commentariis antiquis (на древнегреческом и латинском). Том I. Лейпциг: Teubner.
• Аполлоний Пергский; Heiberg, JL (1893). Apollonii Pergaei quae Graece exstant cum commentariis antiquis (на древнегреческом и латинском). Том II. Лейпциг: Teubner.
• Аполлоний Пергский; Денсмор, Дана (2010). Коники, книги I-III. Санта-Фе (Нью-Мексико): Green Lion Press.
• Аполлоний Пергский; Фрид, Майкл N (2002). Аполлоний Пергский Коники, книга IV: перевод, введение и диаграммы. Санта-Фе, Нью-Мексико: Green Lion Press.
• Аполлоний Пергский; Талиаферро, Р. Кейтсби (1952). «Коникс Букс I-III». В Хатчинс, Роберт Мейнард (ред.). Великие книги западного мира. 11. Евклид, Архимед, Аполлоний Пергский, Никомах. Чикаго, Лондон, Торонто: Британская энциклопедия.
• Аполлоний Пергский; Томас, Айвор (1953). Подборки, иллюстрирующие историю греческой математики. Классическая библиотека Леба. II От Аристарха до Папа. Лондон; Кембридж, Массачусетс: William Heinemann, Ltd.; Издательство Гарвардского университета.
• Аполлоний Пергский; Тумер, ГДж (1990). Conics, книги с V по VII: арабский перевод утраченного греческого оригинала в версии Banū Mūsā. Источники по истории математики и физических наук, 9. Нью-Йорк: Спрингер.
• Аполлоний де Перге, La section droites selon des rapports, Commentaireistorique et mathématique, édition et traduction du texte arabe. Рошди Рашед и Элен Беллоста, Scientia Graeco-Arabica, т. 2. Берлин / Нью-Йорк, Вальтер де Грюйтер, 2010.
• Фрид, Майкл Н .; Унгуру, Сабетай (2001). Аполлоний из Коники Перги: текст, контекст, подтекст. Лейден: Брилл.
• Knorr, W. R. (1986). Древняя традиция геометрических задач. Кембридж, Массачусетс: Birkhauser Boston.
• Нойгебауэр, Отто (1975). История древней математической астрономии. Нью-Йорк: Springer-Verlag.
• Папп Александрийский; Джонс, Александр (1986). Папп Александрийский, книга 7 собрания. Источники по истории математики и физических наук, 8. Нью-Йорк, штат Нью-Йорк: Springer New York.
• Рашед, Рошди; Декорпс-Фулькье, Мишлен; Федершпиль, Мишель, ред. (нет данных). «Коника». Аполлоний де Перге, Coniques: Texte grec et arabe etabli, traduit et commenté. Scientia Graeco-Arabico (на древнегреческом, арабском и французском языках). Берлин, Бостон: Де Грюйтер. Сложить резюме.
• Тумер, Г.Дж. (1970). «Аполлоний Пергский». Словарь научной биографии. 1. Нью-Йорк: Сыновья Чарльза Скрибнера. С. 179–193. ISBN  0-684-10114-9.
• Zeuthen, HG (1886). Die Lehre von den Kegelschnitten im Altertum (на немецком). Копенгаген: Хёст и Зон.

внешняя ссылка

Многие популярные сайты по истории математики, ссылки на которые приведены ниже, ссылаются или анализируют концепции, приписываемые Аполлонию в современных обозначениях и концепциях. Поскольку большая часть Аполлония подлежит интерпретации, и он сам по себе не использует современный словарь или концепции, приведенный ниже анализ может быть неоптимальным или точным. Они представляют собой исторические теории своих авторов.

• Редакторы Encyclopædia Britannica (2006). «Аполлоний Пергский». Британская энциклопедия.
• Кункель, Пол (2016). «Коники Аполлония». Математика Whistler Alley. whistleralley.com. Получено 15 февраля 2017.
• О’Коннор, Джон Дж.; Робертсон, Эдмунд Ф., «Аполлоний Пергский», Архив истории математики MacTutor, Сент-Эндрюсский университет.
• «Математика и математическая астрономия». Брауновский университет.
• «Apollonii Pergaei Conicorum». Цифровая коллекция библиотеки Линды Холл.
• Дэвид Деннис; Сьюзан Аддингтон (2009). «Аполлоний и конические сечения» (PDF). Математические намерения. quadrivium.info.
• Стоудт, Гэри С. «Можете ли вы действительно вывести конические формулы из конуса?». Математическая ассоциация Америки. Получено 28 марта, 2017.
• МакКинни, Колин Брайан Пауэлл (2010). Сопряженные диаметры: Аполлоний Пергский и Евтокий Аскалонский. (Кандидат наук.). Университет Айовы.