Greek mathematics refers to mathematics texts and ideas stemming from the Archaic through the Hellenistic and Roman periods, mostly attested from the late 7th century BC to the 4th century AD, around the shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire region, from Anatolia (Turkey) to Italy and North Africa, but were united by Greek culture and the Greek language.[1] The study of mathematics for its own sake and the use of generalized mathematical theories and proofs is an important difference between Greek mathematics and those of preceding civilizations.[2][3]
Origins and etymology[edit]
Greek mathēmatikē («mathematics») derives from the Ancient Greek: μάθημα, romanized: máthēma, Attic Greek: [má.tʰɛː.ma] Koine Greek: [ˈma.θi.ma], from the verb manthanein, «to learn». Strictly speaking, a máthēma could be any branch of learning, or anything learnt; however, since antiquity certain mathēmata (mainly arithmetic, geometry, astronomy, and harmonics) were granted special status.[4][5]
The origins of Greek mathematics are not well documented.[6][7] The earliest advanced civilizations in Greece and Europe were the Minoan and later Mycenaean civilizations, both of which flourished during the 2nd millennium BC. While these civilizations possessed writing and were capable of advanced engineering, including four-story palaces with drainage and beehive tombs, they left behind no mathematical documents.
Though no direct evidence is available, it is generally thought that the neighboring Babylonian and Egyptian civilizations had an influence on the younger Greek tradition.[8][9][6] Unlike the flourishing of Greek literature in the span of 800 to 600 BC, not much is known about Greek mathematics in this early period—nearly all of the information was passed down through later authors, beginning in the mid-4th century BC.[10][11]
Archaic and Classical periods[edit]
Greek mathematics allegedly began with Thales of Miletus (c. 624–548 BC). Very little is known about his life, although it is generally agreed that he was one of the Seven Wise Men of Greece. According to Proclus, he traveled to Babylon from where he learned mathematics and other subjects, coming up with the proof of what is now called Thales’ Theorem.[12][13]
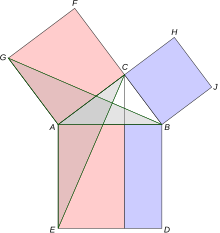
An equally enigmatic figure is Pythagoras of Samos (c. 580–500 BC), who supposedly visited Egypt and Babylon,[11][14] and ultimately settled in Croton, Magna Graecia, where he started a kind of community. Pythagoreans supposedly believed that «all is number» and were keen in looking for mathematical relations between numbers and things.[15] Pythagoras himself was given credit for many later discoveries, including the construction of the five regular solids. However, Aristotle refused to attribute anything specifically to Pythagoras and only discussed the work of the Pythagoreans as a group.[16][17]
Almost half of the material in Euclid’s Elements is customarily attributed to the Pythagoreans, including the discovery of irrationals, attributed to Hippasus (c. 530–450 BC) and Theodorus (fl. 450 BC).[18] The greatest mathematician associated with the group, however, may have been Archytas (c. 435-360 BC), who solved the problem of doubling the cube, identified the harmonic mean, and possibly contributed to optics and mechanics.[18][19] Other mathematicians active in this period, not fully affiliated with any school, include Hippocrates of Chios (c. 470–410 BC), Theaetetus (c. 417–369 BC), and Eudoxus (c. 408–355 BC).
Greek mathematics also drew the attention of philosophers during the Classical period. Plato (c. 428–348 BC), the founder of the Platonic Academy, mentions mathematics in several of his dialogues.[20] While not considered a mathematician, Plato seems to have been influenced by Pythagorean ideas about number and believed that the elements of matter could be broken down into geometric solids.[21] He also believed that geometrical proportions bound the cosmos together rather than physical or mechanical forces.[22] Aristotle (c. 384–322 BC), the founder of the Peripatetic school, often used mathematics to illustrate many of his theories, as when he used geometry in his theory of the rainbow and the theory of proportions in his analysis of motion.[22] Much of the knowledge about ancient Greek mathematics in this period is thanks to records referenced by Aristotle in his own works.[11][23]
Hellenistic and Roman periods[edit]
A fragment from Euclid’s Elements (c. 300 BC), considered the most influential mathematics textbook of all time.[24]
The Hellenistic era began in the late 4th century BC, following Alexander the Great’s conquest of the Eastern Mediterranean, Egypt, Mesopotamia, the Iranian plateau, Central Asia, and parts of India, leading to the spread of the Greek language and culture across these regions. Greek became the lingua franca of scholarship throughout the Hellenistic world, and the mathematics of the Classical period merged with Egyptian and Babylonian mathematics to give rise to a Hellenistic mathematics.[25][26]
Greek mathematics and astronomy reached its acme during the Hellenistic and early Roman periods, and much of the work represented by authors such as Euclid (fl. 300 BC), Archimedes (c. 287–212 BC), Apollonius (c. 240–190 BC), Hipparchus (c. 190–120 BC), and Ptolemy (c. 100–170 AD) was of a very advanced level and rarely mastered outside a small circle.[27] There is also evidence of combining mathematical knowledge with technical or practical applications, as found for instance in the work of Menelaus of Alexandria (c. 70–130 AD), who wrote a work dealing with the geometry of the sphere and its application to astronomical measurements and calculations (Spherica).[28] Similar examples of applied mathematics include the construction of analogue computers like the Antikythera mechanism,[29][30] the accurate measurement of the circumference of the Earth by Eratosthenes (276–194 BC), and the mechanical works of Hero (c. 10–70 AD).[31]
Several centers of learning appeared during the Hellenistic period, of which the most important one was the Musaeum in Alexandria, Egypt, which attracted scholars from across the Hellenistic world (mostly Greek, but also Egyptian, Jewish, Persian, among others).[32][33] Although few in number, Hellenistic mathematicians actively communicated with each other; publication consisted of passing and copying someone’s work among colleagues.[34]
Later mathematicians in the Roman era include Diophantus (c. 214–298 AD), who wrote on polygonal numbers and a work in pre-modern algebra (Arithmetica),[35][36] Pappus of Alexandria (c. 290–350 AD), who compiled many important results in the Collection,[37] Theon of Alexandria (c. 335–405 AD) and his daughter Hypatia (c. 370–415 AD), who edited Ptolemy’s Almagest and other works,[38][39] and Eutocius of Ascalon (c. 480–540 AD), who wrote commentaries on treatises by Archimedes and Apollonius.[40] Although none of these mathematicians, save perhaps Diophantus, had notable original works, they are distinguished for their commentaries and expositions. These commentaries have preserved valuable extracts from works which have perished, or historical allusions which, in the absence of original documents, are precious because of their rarity.[41][42]
Most of the mathematical texts written in Greek survived through the copying of manuscripts over the centuries, though some fragments dating from antiquity have been found in Greece, Egypt, Asia Minor, Mesopotamia, and Sicily.[27]
Achievements[edit]
Greek mathematics constitutes an important period in the history of mathematics: fundamental in respect of geometry and for the idea of formal proof.[43] Greek mathematicians also contributed to number theory, mathematical astronomy, combinatorics, mathematical physics, and, at times, approached ideas close to the integral calculus.[44][45]
Eudoxus of Cnidus developed a theory of proportion that bears resemblance to the modern theory of real numbers using the Dedekind cut, developed by Richard Dedekind, who acknowledged Eudoxus as inspiration.[46][47][48][49]
Euclid collected many previous results and theorems in the Elements, a canon of geometry and elementary number theory for many centuries.[50][51][52]
Archimedes made use of a technique dependent on a form of proof by contradiction to reach answers to problems with an arbitrary degree of accuracy, while specifying the limits within which the answers lay. Known as the method of exhaustion, Archimedes employed it in several of his works, including to approximate the value of π (Measurement of the Circle),[53] and to prove that the area enclosed by a parabola and a straight line is 4/3 times the area of a triangle with equal base and height (Quadrature of the Parabola).[54] Archimedes also showed that the number of grains of sand filling the universe was not uncountable, devising his own counting scheme based on the myriad, which denoted 10,000 (The Sand-Reckoner).[55]
The most characteristic product of Greek mathematics may be the theory of conic sections, which was largely developed in the Hellenistic period, starting with the work of Menaechmus and perfected primarily under Apollonius.[56][57][58] The methods employed in these works made no explicit use of algebra, nor trigonometry, the latter appearing around the time of Hipparchus.[59][60]
Ancient Greek mathematics was not limited to theoretical works but was also used in other activities, such as business transactions and in land mensuration, as evidenced by extant texts where computational procedures and practical considerations took more of a central role.[61][62]
Transmission and the manuscript tradition[edit]
Although the earliest Greek language texts on mathematics that have been found were written after the Hellenistic period, many of these are considered to be copies of works written during and before the Hellenistic period.[63] The two major sources are
- Byzantine codices, written some 500 to 1500 years after their originals, and
- Syriac or Arabic translations of Greek works and Latin translations of the Arabic versions.
Nevertheless, despite the lack of original manuscripts, the dates of Greek mathematics are more certain than the dates of surviving Babylonian or Egyptian sources because a large number of overlapping chronologies exist. Even so, many dates are uncertain; but the doubt is a matter of decades rather than centuries.
Netz has counted 144 ancient authors in the mathematical or exact sciences, from whom only 29 works are extant in Greek: Aristarchus, Autolycus, Philo of Byzantium, Biton, Apollonius, Archimedes, Euclid, Theodosius, Hypsicles, Athenaeus, Geminus, Hero, Apollodorus, Theon of Smyrna, Cleomedes, Nicomachus, Ptolemy, Gaudentius, Anatolius, Aristides Quintilian, Porphyry, Diophantus, Alypius, Damianus, Pappus, Serenus, Theon of Alexandria, Anthemius, and Eutocius.[64]
The following works are extant only in Arabic translations:[65][66]
- Apollonius, Conics books V to VII
- Apollonius, De Rationis Sectione
- Archimedes, Book of Lemmas
- Archimedes, Construction of the Regular Heptagon
- Diocles, On Burning Mirrors
- Diophantus, Arithmetica books IV to VII
- Euclid, On Divisions of Figures
- Euclid, On Weights
- Hero, Catoptrica
- Hero, Mechanica
- Menelaus, Sphaerica
- Pappus, Commentary on Euclid’s Elements book X
- Ptolemy, Optics (extant in Latin from an Arabic translation of the Greek)
- Ptolemy, Planisphaerium
See also[edit]
- Al-Mansur – 2nd Abbasid caliph (r. 754–775)
- Chronology of ancient Greek mathematicians
- Greek numerals – System of writing numbers
- History of geometry – Historical development of geometry
- History of mathematics – Historical development of mathematics
- Timeline of ancient Greek mathematicians – Timeline and summary of ancient Greek mathematicians and their discoveries
Notes[edit]
- ^ Boyer, C.B. (1991), A History of Mathematics (2nd ed.), New York: Wiley, ISBN 0-471-09763-2. p. 48
- ^ Knorr, W. (2000). Mathematics. Greek Thought: A Guide to Classical Knowledge: Harvard University Press. pp. 386–413.
- ^ Schiefsky, Mark (2012-07-20), «The Creation of Second-Order Knowledge in Ancient Greek Science as a Process in the Globalization of Knowledge», The Globalization of Knowledge in History, MPRL – Studies, Berlin: Max-Planck-Gesellschaft zur Förderung der Wissenschaften, ISBN 978-3-945561-23-2, retrieved 2021-03-27
- ^ Heath (1931). «A Manual of Greek Mathematics». Nature. 128 (3235): 5. Bibcode:1931Natur.128..739T. doi:10.1038/128739a0. S2CID 3994109.
- ^ Furner, J. (2020). «Classification of the sciences in Greco-Roman antiquity». www.isko.org. Retrieved 2023-01-09.
- ^ a b Hodgkin, Luke (2005). «Greeks and origins». A History of Mathematics: From Mesopotamia to Modernity. Oxford University Press. ISBN 978-0-19-852937-8.
- ^ Knorr, W. (1981). On the early history of axiomatics: The interaction of mathematics and philosophy in Greek Antiquity. Theory Change, Ancient Axiomatics, and Galileo’s Methodology, Vol. 1: D. Reidel Publishing Co. pp. 145–186.
{{cite book}}: CS1 maint: location (link) - ^ Kahn, C. H. (1991). Some remarks on the origins of Greek science and philosophy. Science and Philosophy in Classical Greece: Garland Publishing Inc. pp. 1–10.
- ^ «Sub-scientific mathematics: undercurrents and missing links in the mathematical technology of the Hellenistic and Roman world | Filosofi og videnskabsteori p? Roskilde Universitetscenter, 3. r?kke: Preprints og reprints».
- ^ Zhmud, Leonid (2008-08-22). The Origin of the History of Science in Classical Antiquity. Peripatoi. De Gruyter. pp. 23–44. doi:10.1515/9783110194326. ISBN 978-3-11-019432-6.
- ^ a b c Boyer & Merzbach (2011) pp. 40–89.
- ^ Panchenko, D. V. (Dmitrii Vadimovich) (1993). «Thales and the Origin of Theoretical Reasoning». Configurations. 1 (3): 387–414. doi:10.1353/con.1993.0024. ISSN 1080-6520.
- ^ Boyer, Carl (1968). A History of Mathematics. pp. 42–43. ISBN 0471543977.
- ^ Heath (2003) pp. 36–111
- ^ Boyer, Carl (1968). A History of Science. p. 45. ISBN 0471543977.
- ^ Cornelli, Gabriele (2016-05-20). «A review of Aristotle’s claim regarding Pythagoreans fundamental Beliefs: All is number?». Filosofia Unisinos / Unisinos Journal of Philosophy. 17 (1): 50–57. doi:10.4013/fsu.2016.171.06. ISSN 1984-8234.
- ^ Hans-Joachim Waschkies, «Introduction» to «Part 1: The Beginning of Greek Mathematics» in Classics in the History of Greek Mathematics, pp. 11–12
- ^ a b Netz, Reviel (2014), Huffman, Carl A. (ed.), «The problem of Pythagorean mathematics», A History of Pythagoreanism, Cambridge: Cambridge University Press, pp. 167–184, ISBN 978-1-107-01439-8, retrieved 2021-05-26
- ^ Burnyeat, M. F. (2005). «Archytas and Optics». Science in Context. 18 (1): 35–53. doi:10.1017/S0269889705000347. ISSN 1474-0664. S2CID 146652622.
- ^ Calian, Florin George (2021-12-09). Numbers, Ontologically Speaking: Plato on Numerosity. Brill. ISBN 978-90-04-46722-4.
- ^ Cherniss, Harold (1951). «Plato as Mathematician». The Review of Metaphysics. 4 (3): 395–425. ISSN 0034-6632. JSTOR 20123223.
- ^ a b Lindberg, David (2008). The Beginnings of Western Science. The University of Chicago Press. pp. 82–110. ISBN 9780226482057.
- ^ Mendell, Henry (26 March 2004). «Aristotle and Mathematics». Stanford Encyclopedia. Retrieved 22 April 2021.
{{cite web}}: CS1 maint: url-status (link) - ^ (Boyer 1991, «Euclid of Alexandria» p. 119)
- ^ Green, P. (1990). Alexander to Actium: The Historical Evolution of the Hellenistic Age (1 ed.). University of California Press. ISBN 978-0-520-08349-3. JSTOR 10.1525/j.ctt130jt89.
- ^ Russo, L. (2004), «Hellenistic Mathematics», The Forgotten Revolution: How Science Was Born in 300 BC and Why It Had to Be Reborn, Berlin, Heidelberg: Springer, pp. 31–55, doi:10.1007/978-3-642-18904-3_3, ISBN 978-3-642-18904-3
- ^ a b Jones, A. (1994). «Greek mathematics to AD 300». Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences: Volume One. pp. 46–57. Retrieved 2021-05-26.
{{cite web}}: CS1 maint: url-status (link) - ^ «Hellenistic Mathematics». The Story of Mathematics — A History of Mathematical Thought from Ancient Times to the Modern Day. Retrieved 2023-01-07.
- ^ Karin Tybjerg (2004-12-01). «Hero of Alexandria’s Mechanical Geometry». Apeiron. 37 (4): 29–56. doi:10.1515/APEIRON.2004.37.4.29. ISSN 2156-7093. S2CID 170916259.
- ^ Edmunds, M. G. (2014-10-02). «The Antikythera mechanism and the mechanical universe». Contemporary Physics. 55 (4): 263–285. Bibcode:2014ConPh..55..263E. doi:10.1080/00107514.2014.927280. S2CID 122403901.
- ^ Russo, Lucio (2004). The Forgotten Revolution. Berlin: Springer. pp. 273–277.
- ^ Luce, J. V. (1988). «Greek Science in its Hellenistic Phase». Hermathena (145): 23–38. ISSN 0018-0750. JSTOR 23040930.
- ^ Berrey, M. (2017). Hellenistic Science at Court. De Gruyter. doi:10.1515/9783110541939. ISBN 978-3-11-054193-9.
- ^ Acerbi, F. (2018). Keyser, Paul T; Scarborough, John (eds.). «Hellenistic Mathematics». Oxford Handbook of Science and Medicine in the Classical World. pp. 268–292. doi:10.1093/oxfordhb/9780199734146.013.69. ISBN 978-0-19-973414-6. Retrieved 2021-05-26.
{{cite web}}: CS1 maint: url-status (link) - ^ Acerbi, F. (2011). «Completing Diophantus, De polygonis numeris, prop. 5». Historia Mathematica. 38 (4): 548–560. doi:10.1016/j.hm.2011.05.002. ISSN 0315-0860.
- ^ Christianidis, J.; Oaks, J. (2013). «Practicing algebra in late antiquity: The problem-solving of Diophantus of Alexandria». Historia Mathematica. 40 (2): 127–163. doi:10.1016/j.hm.2012.09.001. ISSN 0315-0860.
- ^ Rideout, Bronwyn (2008). Pappus Reborn : Pappus of Alexandria and the Changing Face of Analysis and Synthesis in Late Antiquity (Thesis). doi:10.26021/3834.
- ^ Lambrou, M. (2003). «Theon of Alexandria and Hypatia». History of the Ancient World. Retrieved 2021-05-26.
{{cite web}}: CS1 maint: url-status (link) - ^ Cameron, A. (1990). «Isidore of Miletus and Hypatia: On the Editing of Mathematical Texts». Greek, Roman, and Byzantine Studies. 31 (1): 103–127. ISSN 2159-3159.
- ^ Mansfeld, J. (2016). Prolegomena Mathematica: From Apollonius of Perga to the Late Neoplatonism. Brill. ISBN 978-90-04-32105-2.
- ^ Mansfeld, J. (2016). Prolegomena Mathematica: From Apollonius of Perga to the Late Neoplatonism. With an Appendix on Pappus and the History of Platonism. Brill. ISBN 978-90-04-32105-2.
- ^ Heath, Thomas (1921). A History of Greek Mathematics. Humphrey Milford.
- ^ Grant, H.; Kleiner, I. (2015), «Axiomatics—Euclid’s and Hilbert’s: From Material to Formal», Turning Points in the History of Mathematics, Springer, pp. 1–8, doi:10.1007/978-1-4939-3264-1_1, ISBN 978-1-4939-3264-1
- ^ Knorr, W. (1996). The method of indivisibles in Ancient Geometry. Vita Mathematica: MAA Press. pp. 67–86.
- ^ Powers, J. (2020). Did Archimedes do calculus? History of Mathematics Special Interest Group of the MAA [1]
- ^ Stein, Howard (1990-08-01). «Eudoxos and Dedekind: On the ancient Greek theory of ratios and its relation to modern mathematics». Synthese. 84 (2): 163–211. doi:10.1007/BF00485377. ISSN 1573-0964. S2CID 46974744.
- ^ Wigderson, Y. (April 2019). Eudoxus, the most important mathematician you’ve never heard of. https://web.stanford.edu/~yuvalwig/math/teaching/Eudoxus.pdf Archived 2021-07-28 at the Wayback Machine
- ^ Filep, L. (2003). «Proportion theory in Greek mathematics». Acta Mathematica Academiae Paedagogicae Nyí regyháziensis. 19: 167–174.
- ^ J J O’Connor and E F Robertson (April 1999). «Eudoxus of Cnidus». MacTutor History of Mathematics archive. University of St. Andrews. Retrieved 18 April 2011.
- ^ Artmann, Benno (1999). Euclid—The Creation of Mathematics. New York: Springer-Verlag. ISBN 978-0-387-98423-0.
- ^ MUELLER, IAN (1969-12-01). «Euclid’s Elements and the Axiomatic Method». The British Journal for the Philosophy of Science. 20 (4): 289–309. doi:10.1093/bjps/20.4.289. ISSN 0007-0882.
- ^ Pierce, D. (2015). The Foundations of Arithmetic in Euclid.
- ^ Knorr, Wilbur R. (1976). «Archimedes and the Measurement of the Circle: A New Interpretation». Archive for History of Exact Sciences. 15 (2): 115–140. doi:10.1007/BF00348496. ISSN 0003-9519. JSTOR 41133444. S2CID 120954547.
- ^ Swain, Gordon; Dence, Thomas (1998). «Archimedes’ Quadrature of the Parabola Revisited». Mathematics Magazine. 71 (2): 123–130. doi:10.2307/2691014. ISSN 0025-570X. JSTOR 2691014.
- ^ Reviel Netz (2003-12-01). «The Goal of Archimedes’ Sand Reckoner». Apeiron. 36 (4): 251–290. doi:10.1515/APEIRON.2003.36.4.251. ISSN 2156-7093. S2CID 147307969.
- ^ Court, N. A. (1961). «The problem of Apollonius». The Mathematics Teacher. 54 (6): 444–452. doi:10.5951/MT.54.6.0444. ISSN 0025-5769. JSTOR 27956431.
- ^ Knorr, Wilbur Richard (1981). «The Hyperbola-Construction in the Conics, Book II: Ancient Variations on a Theorem of Apollonius». Centaurus. 25 (3): 253–291. Bibcode:1981Cent…25..253K. doi:10.1111/j.1600-0498.1981.tb00647.x. ISSN 1600-0498.
- ^ Baltus, Christopher (2020), Baltus, Christopher (ed.), «Conics in Greek Geometry: Apollonius, Harmonic Division, and Later Greek Geometry», Collineations and Conic Sections: An Introduction to Projective Geometry in its History, Cham: Springer International Publishing, pp. 45–57, doi:10.1007/978-3-030-46287-1_4, ISBN 978-3-030-46287-1, S2CID 226745369, retrieved 2021-03-27
- ^ Toomer, G. J. (1974). «The Chord Table of Hipparchus and the Early History of Greek Trigonometry». Centaurus. 18 (1): 6–28. Bibcode:1974Cent…18….6T. doi:10.1111/j.1600-0498.1974.tb00205.x. ISSN 1600-0498.
- ^ Duke, D. (2011). «The very early history of trigonometry» (PDF). DIO: The International Journal of Scientific History. 17: 34–42.
- ^ Høyrup, J. (1990). «Sub-scientific mathematics: Undercurrents and missing links in the mathematical technology of the Hellenistic and Roman world». Filosofi og Videnskabsteori P? Roskilde Universitetscenter, 3. R?kke: Preprints og Reprints.
- ^ Robbins, F. E. (1934). «Greco-Egyptian Arithmetical Problems: P. Mich. 4966». Isis. 22 (1): 95–103. doi:10.1086/346874. S2CID 144052363.
- ^ J J O’Connor and E F Robertson (October 1999). «How do we know about Greek mathematics?». The MacTutor History of Mathematics archive. University of St. Andrews. Archived from the original on 30 January 2000. Retrieved 18 April 2011.
- ^ Netz, R. The Bibliosphere of Ancient Science (Outside of Alexandria). N.T.M. 19, 239 (2011). https://doi.org/10.1007/s00048-011-0057-2
- ^ Lorch, R. (2001). Greek-Arabic-Latin: The Transmission of Mathematical Texts in the Middle Ages. Science in Context, 14(1–2), 313–331. doi:10.1017/S0269889701000114
- ^ Toomer, G.J. Lost greek mathematical works in arabic translation. The Mathematical Intelligencer 6, 32–38 (1984). https://doi.org/10.1007/BF03024153
References[edit]
- Boyer, Carl B. (1985), A History of Mathematics, Princeton University Press, ISBN 978-0-691-02391-5
- Boyer, Carl B.; Merzbach, Uta C. (2011), A History of Mathematics (3rd ed.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8
- Jean Christianidis, ed. (2004), Classics in the History of Greek Mathematics, Kluwer Academic Publishers, ISBN 978-1-4020-0081-2
- Cooke, Roger (1997), The History of Mathematics: A Brief Course, Wiley-Interscience, ISBN 978-0-471-18082-1
- Derbyshire, John (2006), Unknown Quantity: A Real And Imaginary History of Algebra, Joseph Henry Press, ISBN 978-0-309-09657-7
- Stillwell, John (2004), Mathematics and its History (2nd ed.), Springer Science + Business Media Inc., ISBN 978-0-387-95336-6
- Burton, David M. (1997), The History of Mathematics: An Introduction (3rd ed.), The McGraw-Hill Companies, Inc., ISBN 978-0-07-009465-9
- Heath, Thomas Little (1981) [First published 1921], A History of Greek Mathematics, Dover publications, ISBN 978-0-486-24073-2
- Heath, Thomas Little (2003) [First published 1931], A Manual of Greek Mathematics, Dover publications, ISBN 978-0-486-43231-1
- Szabo, Arpad (1978) [First published 1978], The Beginnings of Greek Mathematics, Reidel & Akademiai Kiado, ISBN 978-963-05-1416-3
External links[edit]
- Vatican Exhibit
- Famous Greek Mathematicians
Greek mathematics refers to mathematics texts and ideas stemming from the Archaic through the Hellenistic and Roman periods, mostly attested from the late 7th century BC to the 4th century AD, around the shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire region, from Anatolia (Turkey) to Italy and North Africa, but were united by Greek culture and the Greek language.[1] The study of mathematics for its own sake and the use of generalized mathematical theories and proofs is an important difference between Greek mathematics and those of preceding civilizations.[2][3]
Origins and etymology[edit]
Greek mathēmatikē («mathematics») derives from the Ancient Greek: μάθημα, romanized: máthēma, Attic Greek: [má.tʰɛː.ma] Koine Greek: [ˈma.θi.ma], from the verb manthanein, «to learn». Strictly speaking, a máthēma could be any branch of learning, or anything learnt; however, since antiquity certain mathēmata (mainly arithmetic, geometry, astronomy, and harmonics) were granted special status.[4][5]
The origins of Greek mathematics are not well documented.[6][7] The earliest advanced civilizations in Greece and Europe were the Minoan and later Mycenaean civilizations, both of which flourished during the 2nd millennium BC. While these civilizations possessed writing and were capable of advanced engineering, including four-story palaces with drainage and beehive tombs, they left behind no mathematical documents.
Though no direct evidence is available, it is generally thought that the neighboring Babylonian and Egyptian civilizations had an influence on the younger Greek tradition.[8][9][6] Unlike the flourishing of Greek literature in the span of 800 to 600 BC, not much is known about Greek mathematics in this early period—nearly all of the information was passed down through later authors, beginning in the mid-4th century BC.[10][11]
Archaic and Classical periods[edit]
Greek mathematics allegedly began with Thales of Miletus (c. 624–548 BC). Very little is known about his life, although it is generally agreed that he was one of the Seven Wise Men of Greece. According to Proclus, he traveled to Babylon from where he learned mathematics and other subjects, coming up with the proof of what is now called Thales’ Theorem.[12][13]
An equally enigmatic figure is Pythagoras of Samos (c. 580–500 BC), who supposedly visited Egypt and Babylon,[11][14] and ultimately settled in Croton, Magna Graecia, where he started a kind of community. Pythagoreans supposedly believed that «all is number» and were keen in looking for mathematical relations between numbers and things.[15] Pythagoras himself was given credit for many later discoveries, including the construction of the five regular solids. However, Aristotle refused to attribute anything specifically to Pythagoras and only discussed the work of the Pythagoreans as a group.[16][17]
Almost half of the material in Euclid’s Elements is customarily attributed to the Pythagoreans, including the discovery of irrationals, attributed to Hippasus (c. 530–450 BC) and Theodorus (fl. 450 BC).[18] The greatest mathematician associated with the group, however, may have been Archytas (c. 435-360 BC), who solved the problem of doubling the cube, identified the harmonic mean, and possibly contributed to optics and mechanics.[18][19] Other mathematicians active in this period, not fully affiliated with any school, include Hippocrates of Chios (c. 470–410 BC), Theaetetus (c. 417–369 BC), and Eudoxus (c. 408–355 BC).
Greek mathematics also drew the attention of philosophers during the Classical period. Plato (c. 428–348 BC), the founder of the Platonic Academy, mentions mathematics in several of his dialogues.[20] While not considered a mathematician, Plato seems to have been influenced by Pythagorean ideas about number and believed that the elements of matter could be broken down into geometric solids.[21] He also believed that geometrical proportions bound the cosmos together rather than physical or mechanical forces.[22] Aristotle (c. 384–322 BC), the founder of the Peripatetic school, often used mathematics to illustrate many of his theories, as when he used geometry in his theory of the rainbow and the theory of proportions in his analysis of motion.[22] Much of the knowledge about ancient Greek mathematics in this period is thanks to records referenced by Aristotle in his own works.[11][23]
Hellenistic and Roman periods[edit]
A fragment from Euclid’s Elements (c. 300 BC), considered the most influential mathematics textbook of all time.[24]
The Hellenistic era began in the late 4th century BC, following Alexander the Great’s conquest of the Eastern Mediterranean, Egypt, Mesopotamia, the Iranian plateau, Central Asia, and parts of India, leading to the spread of the Greek language and culture across these regions. Greek became the lingua franca of scholarship throughout the Hellenistic world, and the mathematics of the Classical period merged with Egyptian and Babylonian mathematics to give rise to a Hellenistic mathematics.[25][26]
Greek mathematics and astronomy reached its acme during the Hellenistic and early Roman periods, and much of the work represented by authors such as Euclid (fl. 300 BC), Archimedes (c. 287–212 BC), Apollonius (c. 240–190 BC), Hipparchus (c. 190–120 BC), and Ptolemy (c. 100–170 AD) was of a very advanced level and rarely mastered outside a small circle.[27] There is also evidence of combining mathematical knowledge with technical or practical applications, as found for instance in the work of Menelaus of Alexandria (c. 70–130 AD), who wrote a work dealing with the geometry of the sphere and its application to astronomical measurements and calculations (Spherica).[28] Similar examples of applied mathematics include the construction of analogue computers like the Antikythera mechanism,[29][30] the accurate measurement of the circumference of the Earth by Eratosthenes (276–194 BC), and the mechanical works of Hero (c. 10–70 AD).[31]
Several centers of learning appeared during the Hellenistic period, of which the most important one was the Musaeum in Alexandria, Egypt, which attracted scholars from across the Hellenistic world (mostly Greek, but also Egyptian, Jewish, Persian, among others).[32][33] Although few in number, Hellenistic mathematicians actively communicated with each other; publication consisted of passing and copying someone’s work among colleagues.[34]
Later mathematicians in the Roman era include Diophantus (c. 214–298 AD), who wrote on polygonal numbers and a work in pre-modern algebra (Arithmetica),[35][36] Pappus of Alexandria (c. 290–350 AD), who compiled many important results in the Collection,[37] Theon of Alexandria (c. 335–405 AD) and his daughter Hypatia (c. 370–415 AD), who edited Ptolemy’s Almagest and other works,[38][39] and Eutocius of Ascalon (c. 480–540 AD), who wrote commentaries on treatises by Archimedes and Apollonius.[40] Although none of these mathematicians, save perhaps Diophantus, had notable original works, they are distinguished for their commentaries and expositions. These commentaries have preserved valuable extracts from works which have perished, or historical allusions which, in the absence of original documents, are precious because of their rarity.[41][42]
Most of the mathematical texts written in Greek survived through the copying of manuscripts over the centuries, though some fragments dating from antiquity have been found in Greece, Egypt, Asia Minor, Mesopotamia, and Sicily.[27]
Achievements[edit]
Greek mathematics constitutes an important period in the history of mathematics: fundamental in respect of geometry and for the idea of formal proof.[43] Greek mathematicians also contributed to number theory, mathematical astronomy, combinatorics, mathematical physics, and, at times, approached ideas close to the integral calculus.[44][45]
Eudoxus of Cnidus developed a theory of proportion that bears resemblance to the modern theory of real numbers using the Dedekind cut, developed by Richard Dedekind, who acknowledged Eudoxus as inspiration.[46][47][48][49]
Euclid collected many previous results and theorems in the Elements, a canon of geometry and elementary number theory for many centuries.[50][51][52]
Archimedes made use of a technique dependent on a form of proof by contradiction to reach answers to problems with an arbitrary degree of accuracy, while specifying the limits within which the answers lay. Known as the method of exhaustion, Archimedes employed it in several of his works, including to approximate the value of π (Measurement of the Circle),[53] and to prove that the area enclosed by a parabola and a straight line is 4/3 times the area of a triangle with equal base and height (Quadrature of the Parabola).[54] Archimedes also showed that the number of grains of sand filling the universe was not uncountable, devising his own counting scheme based on the myriad, which denoted 10,000 (The Sand-Reckoner).[55]
The most characteristic product of Greek mathematics may be the theory of conic sections, which was largely developed in the Hellenistic period, starting with the work of Menaechmus and perfected primarily under Apollonius.[56][57][58] The methods employed in these works made no explicit use of algebra, nor trigonometry, the latter appearing around the time of Hipparchus.[59][60]
Ancient Greek mathematics was not limited to theoretical works but was also used in other activities, such as business transactions and in land mensuration, as evidenced by extant texts where computational procedures and practical considerations took more of a central role.[61][62]
Transmission and the manuscript tradition[edit]
Although the earliest Greek language texts on mathematics that have been found were written after the Hellenistic period, many of these are considered to be copies of works written during and before the Hellenistic period.[63] The two major sources are
- Byzantine codices, written some 500 to 1500 years after their originals, and
- Syriac or Arabic translations of Greek works and Latin translations of the Arabic versions.
Nevertheless, despite the lack of original manuscripts, the dates of Greek mathematics are more certain than the dates of surviving Babylonian or Egyptian sources because a large number of overlapping chronologies exist. Even so, many dates are uncertain; but the doubt is a matter of decades rather than centuries.
Netz has counted 144 ancient authors in the mathematical or exact sciences, from whom only 29 works are extant in Greek: Aristarchus, Autolycus, Philo of Byzantium, Biton, Apollonius, Archimedes, Euclid, Theodosius, Hypsicles, Athenaeus, Geminus, Hero, Apollodorus, Theon of Smyrna, Cleomedes, Nicomachus, Ptolemy, Gaudentius, Anatolius, Aristides Quintilian, Porphyry, Diophantus, Alypius, Damianus, Pappus, Serenus, Theon of Alexandria, Anthemius, and Eutocius.[64]
The following works are extant only in Arabic translations:[65][66]
- Apollonius, Conics books V to VII
- Apollonius, De Rationis Sectione
- Archimedes, Book of Lemmas
- Archimedes, Construction of the Regular Heptagon
- Diocles, On Burning Mirrors
- Diophantus, Arithmetica books IV to VII
- Euclid, On Divisions of Figures
- Euclid, On Weights
- Hero, Catoptrica
- Hero, Mechanica
- Menelaus, Sphaerica
- Pappus, Commentary on Euclid’s Elements book X
- Ptolemy, Optics (extant in Latin from an Arabic translation of the Greek)
- Ptolemy, Planisphaerium
See also[edit]
- Al-Mansur – 2nd Abbasid caliph (r. 754–775)
- Chronology of ancient Greek mathematicians
- Greek numerals – System of writing numbers
- History of geometry – Historical development of geometry
- History of mathematics – Historical development of mathematics
- Timeline of ancient Greek mathematicians – Timeline and summary of ancient Greek mathematicians and their discoveries
Notes[edit]
- ^ Boyer, C.B. (1991), A History of Mathematics (2nd ed.), New York: Wiley, ISBN 0-471-09763-2. p. 48
- ^ Knorr, W. (2000). Mathematics. Greek Thought: A Guide to Classical Knowledge: Harvard University Press. pp. 386–413.
- ^ Schiefsky, Mark (2012-07-20), «The Creation of Second-Order Knowledge in Ancient Greek Science as a Process in the Globalization of Knowledge», The Globalization of Knowledge in History, MPRL – Studies, Berlin: Max-Planck-Gesellschaft zur Förderung der Wissenschaften, ISBN 978-3-945561-23-2, retrieved 2021-03-27
- ^ Heath (1931). «A Manual of Greek Mathematics». Nature. 128 (3235): 5. Bibcode:1931Natur.128..739T. doi:10.1038/128739a0. S2CID 3994109.
- ^ Furner, J. (2020). «Classification of the sciences in Greco-Roman antiquity». www.isko.org. Retrieved 2023-01-09.
- ^ a b Hodgkin, Luke (2005). «Greeks and origins». A History of Mathematics: From Mesopotamia to Modernity. Oxford University Press. ISBN 978-0-19-852937-8.
- ^ Knorr, W. (1981). On the early history of axiomatics: The interaction of mathematics and philosophy in Greek Antiquity. Theory Change, Ancient Axiomatics, and Galileo’s Methodology, Vol. 1: D. Reidel Publishing Co. pp. 145–186.
{{cite book}}: CS1 maint: location (link) - ^ Kahn, C. H. (1991). Some remarks on the origins of Greek science and philosophy. Science and Philosophy in Classical Greece: Garland Publishing Inc. pp. 1–10.
- ^ «Sub-scientific mathematics: undercurrents and missing links in the mathematical technology of the Hellenistic and Roman world | Filosofi og videnskabsteori p? Roskilde Universitetscenter, 3. r?kke: Preprints og reprints».
- ^ Zhmud, Leonid (2008-08-22). The Origin of the History of Science in Classical Antiquity. Peripatoi. De Gruyter. pp. 23–44. doi:10.1515/9783110194326. ISBN 978-3-11-019432-6.
- ^ a b c Boyer & Merzbach (2011) pp. 40–89.
- ^ Panchenko, D. V. (Dmitrii Vadimovich) (1993). «Thales and the Origin of Theoretical Reasoning». Configurations. 1 (3): 387–414. doi:10.1353/con.1993.0024. ISSN 1080-6520.
- ^ Boyer, Carl (1968). A History of Mathematics. pp. 42–43. ISBN 0471543977.
- ^ Heath (2003) pp. 36–111
- ^ Boyer, Carl (1968). A History of Science. p. 45. ISBN 0471543977.
- ^ Cornelli, Gabriele (2016-05-20). «A review of Aristotle’s claim regarding Pythagoreans fundamental Beliefs: All is number?». Filosofia Unisinos / Unisinos Journal of Philosophy. 17 (1): 50–57. doi:10.4013/fsu.2016.171.06. ISSN 1984-8234.
- ^ Hans-Joachim Waschkies, «Introduction» to «Part 1: The Beginning of Greek Mathematics» in Classics in the History of Greek Mathematics, pp. 11–12
- ^ a b Netz, Reviel (2014), Huffman, Carl A. (ed.), «The problem of Pythagorean mathematics», A History of Pythagoreanism, Cambridge: Cambridge University Press, pp. 167–184, ISBN 978-1-107-01439-8, retrieved 2021-05-26
- ^ Burnyeat, M. F. (2005). «Archytas and Optics». Science in Context. 18 (1): 35–53. doi:10.1017/S0269889705000347. ISSN 1474-0664. S2CID 146652622.
- ^ Calian, Florin George (2021-12-09). Numbers, Ontologically Speaking: Plato on Numerosity. Brill. ISBN 978-90-04-46722-4.
- ^ Cherniss, Harold (1951). «Plato as Mathematician». The Review of Metaphysics. 4 (3): 395–425. ISSN 0034-6632. JSTOR 20123223.
- ^ a b Lindberg, David (2008). The Beginnings of Western Science. The University of Chicago Press. pp. 82–110. ISBN 9780226482057.
- ^ Mendell, Henry (26 March 2004). «Aristotle and Mathematics». Stanford Encyclopedia. Retrieved 22 April 2021.
{{cite web}}: CS1 maint: url-status (link) - ^ (Boyer 1991, «Euclid of Alexandria» p. 119)
- ^ Green, P. (1990). Alexander to Actium: The Historical Evolution of the Hellenistic Age (1 ed.). University of California Press. ISBN 978-0-520-08349-3. JSTOR 10.1525/j.ctt130jt89.
- ^ Russo, L. (2004), «Hellenistic Mathematics», The Forgotten Revolution: How Science Was Born in 300 BC and Why It Had to Be Reborn, Berlin, Heidelberg: Springer, pp. 31–55, doi:10.1007/978-3-642-18904-3_3, ISBN 978-3-642-18904-3
- ^ a b Jones, A. (1994). «Greek mathematics to AD 300». Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences: Volume One. pp. 46–57. Retrieved 2021-05-26.
{{cite web}}: CS1 maint: url-status (link) - ^ «Hellenistic Mathematics». The Story of Mathematics — A History of Mathematical Thought from Ancient Times to the Modern Day. Retrieved 2023-01-07.
- ^ Karin Tybjerg (2004-12-01). «Hero of Alexandria’s Mechanical Geometry». Apeiron. 37 (4): 29–56. doi:10.1515/APEIRON.2004.37.4.29. ISSN 2156-7093. S2CID 170916259.
- ^ Edmunds, M. G. (2014-10-02). «The Antikythera mechanism and the mechanical universe». Contemporary Physics. 55 (4): 263–285. Bibcode:2014ConPh..55..263E. doi:10.1080/00107514.2014.927280. S2CID 122403901.
- ^ Russo, Lucio (2004). The Forgotten Revolution. Berlin: Springer. pp. 273–277.
- ^ Luce, J. V. (1988). «Greek Science in its Hellenistic Phase». Hermathena (145): 23–38. ISSN 0018-0750. JSTOR 23040930.
- ^ Berrey, M. (2017). Hellenistic Science at Court. De Gruyter. doi:10.1515/9783110541939. ISBN 978-3-11-054193-9.
- ^ Acerbi, F. (2018). Keyser, Paul T; Scarborough, John (eds.). «Hellenistic Mathematics». Oxford Handbook of Science and Medicine in the Classical World. pp. 268–292. doi:10.1093/oxfordhb/9780199734146.013.69. ISBN 978-0-19-973414-6. Retrieved 2021-05-26.
{{cite web}}: CS1 maint: url-status (link) - ^ Acerbi, F. (2011). «Completing Diophantus, De polygonis numeris, prop. 5». Historia Mathematica. 38 (4): 548–560. doi:10.1016/j.hm.2011.05.002. ISSN 0315-0860.
- ^ Christianidis, J.; Oaks, J. (2013). «Practicing algebra in late antiquity: The problem-solving of Diophantus of Alexandria». Historia Mathematica. 40 (2): 127–163. doi:10.1016/j.hm.2012.09.001. ISSN 0315-0860.
- ^ Rideout, Bronwyn (2008). Pappus Reborn : Pappus of Alexandria and the Changing Face of Analysis and Synthesis in Late Antiquity (Thesis). doi:10.26021/3834.
- ^ Lambrou, M. (2003). «Theon of Alexandria and Hypatia». History of the Ancient World. Retrieved 2021-05-26.
{{cite web}}: CS1 maint: url-status (link) - ^ Cameron, A. (1990). «Isidore of Miletus and Hypatia: On the Editing of Mathematical Texts». Greek, Roman, and Byzantine Studies. 31 (1): 103–127. ISSN 2159-3159.
- ^ Mansfeld, J. (2016). Prolegomena Mathematica: From Apollonius of Perga to the Late Neoplatonism. Brill. ISBN 978-90-04-32105-2.
- ^ Mansfeld, J. (2016). Prolegomena Mathematica: From Apollonius of Perga to the Late Neoplatonism. With an Appendix on Pappus and the History of Platonism. Brill. ISBN 978-90-04-32105-2.
- ^ Heath, Thomas (1921). A History of Greek Mathematics. Humphrey Milford.
- ^ Grant, H.; Kleiner, I. (2015), «Axiomatics—Euclid’s and Hilbert’s: From Material to Formal», Turning Points in the History of Mathematics, Springer, pp. 1–8, doi:10.1007/978-1-4939-3264-1_1, ISBN 978-1-4939-3264-1
- ^ Knorr, W. (1996). The method of indivisibles in Ancient Geometry. Vita Mathematica: MAA Press. pp. 67–86.
- ^ Powers, J. (2020). Did Archimedes do calculus? History of Mathematics Special Interest Group of the MAA [1]
- ^ Stein, Howard (1990-08-01). «Eudoxos and Dedekind: On the ancient Greek theory of ratios and its relation to modern mathematics». Synthese. 84 (2): 163–211. doi:10.1007/BF00485377. ISSN 1573-0964. S2CID 46974744.
- ^ Wigderson, Y. (April 2019). Eudoxus, the most important mathematician you’ve never heard of. https://web.stanford.edu/~yuvalwig/math/teaching/Eudoxus.pdf Archived 2021-07-28 at the Wayback Machine
- ^ Filep, L. (2003). «Proportion theory in Greek mathematics». Acta Mathematica Academiae Paedagogicae Nyí regyháziensis. 19: 167–174.
- ^ J J O’Connor and E F Robertson (April 1999). «Eudoxus of Cnidus». MacTutor History of Mathematics archive. University of St. Andrews. Retrieved 18 April 2011.
- ^ Artmann, Benno (1999). Euclid—The Creation of Mathematics. New York: Springer-Verlag. ISBN 978-0-387-98423-0.
- ^ MUELLER, IAN (1969-12-01). «Euclid’s Elements and the Axiomatic Method». The British Journal for the Philosophy of Science. 20 (4): 289–309. doi:10.1093/bjps/20.4.289. ISSN 0007-0882.
- ^ Pierce, D. (2015). The Foundations of Arithmetic in Euclid.
- ^ Knorr, Wilbur R. (1976). «Archimedes and the Measurement of the Circle: A New Interpretation». Archive for History of Exact Sciences. 15 (2): 115–140. doi:10.1007/BF00348496. ISSN 0003-9519. JSTOR 41133444. S2CID 120954547.
- ^ Swain, Gordon; Dence, Thomas (1998). «Archimedes’ Quadrature of the Parabola Revisited». Mathematics Magazine. 71 (2): 123–130. doi:10.2307/2691014. ISSN 0025-570X. JSTOR 2691014.
- ^ Reviel Netz (2003-12-01). «The Goal of Archimedes’ Sand Reckoner». Apeiron. 36 (4): 251–290. doi:10.1515/APEIRON.2003.36.4.251. ISSN 2156-7093. S2CID 147307969.
- ^ Court, N. A. (1961). «The problem of Apollonius». The Mathematics Teacher. 54 (6): 444–452. doi:10.5951/MT.54.6.0444. ISSN 0025-5769. JSTOR 27956431.
- ^ Knorr, Wilbur Richard (1981). «The Hyperbola-Construction in the Conics, Book II: Ancient Variations on a Theorem of Apollonius». Centaurus. 25 (3): 253–291. Bibcode:1981Cent…25..253K. doi:10.1111/j.1600-0498.1981.tb00647.x. ISSN 1600-0498.
- ^ Baltus, Christopher (2020), Baltus, Christopher (ed.), «Conics in Greek Geometry: Apollonius, Harmonic Division, and Later Greek Geometry», Collineations and Conic Sections: An Introduction to Projective Geometry in its History, Cham: Springer International Publishing, pp. 45–57, doi:10.1007/978-3-030-46287-1_4, ISBN 978-3-030-46287-1, S2CID 226745369, retrieved 2021-03-27
- ^ Toomer, G. J. (1974). «The Chord Table of Hipparchus and the Early History of Greek Trigonometry». Centaurus. 18 (1): 6–28. Bibcode:1974Cent…18….6T. doi:10.1111/j.1600-0498.1974.tb00205.x. ISSN 1600-0498.
- ^ Duke, D. (2011). «The very early history of trigonometry» (PDF). DIO: The International Journal of Scientific History. 17: 34–42.
- ^ Høyrup, J. (1990). «Sub-scientific mathematics: Undercurrents and missing links in the mathematical technology of the Hellenistic and Roman world». Filosofi og Videnskabsteori P? Roskilde Universitetscenter, 3. R?kke: Preprints og Reprints.
- ^ Robbins, F. E. (1934). «Greco-Egyptian Arithmetical Problems: P. Mich. 4966». Isis. 22 (1): 95–103. doi:10.1086/346874. S2CID 144052363.
- ^ J J O’Connor and E F Robertson (October 1999). «How do we know about Greek mathematics?». The MacTutor History of Mathematics archive. University of St. Andrews. Archived from the original on 30 January 2000. Retrieved 18 April 2011.
- ^ Netz, R. The Bibliosphere of Ancient Science (Outside of Alexandria). N.T.M. 19, 239 (2011). https://doi.org/10.1007/s00048-011-0057-2
- ^ Lorch, R. (2001). Greek-Arabic-Latin: The Transmission of Mathematical Texts in the Middle Ages. Science in Context, 14(1–2), 313–331. doi:10.1017/S0269889701000114
- ^ Toomer, G.J. Lost greek mathematical works in arabic translation. The Mathematical Intelligencer 6, 32–38 (1984). https://doi.org/10.1007/BF03024153
References[edit]
- Boyer, Carl B. (1985), A History of Mathematics, Princeton University Press, ISBN 978-0-691-02391-5
- Boyer, Carl B.; Merzbach, Uta C. (2011), A History of Mathematics (3rd ed.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8
- Jean Christianidis, ed. (2004), Classics in the History of Greek Mathematics, Kluwer Academic Publishers, ISBN 978-1-4020-0081-2
- Cooke, Roger (1997), The History of Mathematics: A Brief Course, Wiley-Interscience, ISBN 978-0-471-18082-1
- Derbyshire, John (2006), Unknown Quantity: A Real And Imaginary History of Algebra, Joseph Henry Press, ISBN 978-0-309-09657-7
- Stillwell, John (2004), Mathematics and its History (2nd ed.), Springer Science + Business Media Inc., ISBN 978-0-387-95336-6
- Burton, David M. (1997), The History of Mathematics: An Introduction (3rd ed.), The McGraw-Hill Companies, Inc., ISBN 978-0-07-009465-9
- Heath, Thomas Little (1981) [First published 1921], A History of Greek Mathematics, Dover publications, ISBN 978-0-486-24073-2
- Heath, Thomas Little (2003) [First published 1931], A Manual of Greek Mathematics, Dover publications, ISBN 978-0-486-43231-1
- Szabo, Arpad (1978) [First published 1978], The Beginnings of Greek Mathematics, Reidel & Akademiai Kiado, ISBN 978-963-05-1416-3
External links[edit]
- Vatican Exhibit
- Famous Greek Mathematicians
-
- Данная статья — часть обзора История математики.
Муза геометрии (Лувр)
Содержание
- 1 Введение
- 2 Источники
- 3 Начальный период
- 4 Пифагорейская школа
- 5 V век до н. э. — Зенон, Демокрит
- 6 IV век до н. э. — Платон, Евдокс
- 7 III век до н. э. — Евклид, Архимед, Аполлоний
- 8 Упадок античной науки
- 9 Заключение
- 10 Литература
- 11 Ссылки
- 12 Примечания
Введение
Понятие древнегреческая математика охватывает достижения грекоязычных математиков, живших в период между VI веком до н. э. и V веком н. э.
Математика как наука родилась в Греции[1] [2]. В странах-современниках Эллады математика использовалась либо для обыденных нужд (подсчёты, измерения), либо, наоборот, для магических ритуалов, имевших целью выяснить волю богов (астрология, нумерология и т. п.). Греки подошли к делу с другой стороны: они выдвинули тезис «Числа правят миром». Или, как сформулировал эту же мысль Галилей два тысячелетия спустя: «книга природы написана на языке математики»[3].
Греки проверили справедливость этого тезиса в тех областях, где сумели: астрономия, оптика, музыка, геометрия, позже — механика. Всюду были отмечены впечатляющие успехи: математическая модель обладала неоспоримой предсказательной силой. Одновременно греки создали методологию математики и завершили превращение её из свода полуэвристических алгоритмов в целостную систему знаний. Основой этой системы впервые стал дедуктивный метод, показывающий, как из известных истин выводить новые, причём логика вывода гарантирует истинность новых результатов. Дедуктивный метод также позволяет выявить неочевидные связи между понятиями, научными фактами и областями математики.
Источники
Бо́льшая часть античных сочинений по математике не дошла до наших дней и известна только по упоминаниям позднейших авторов и комментаторов, в первую очередь Паппа Александрийского (III век), Прокла (V век), Симпликия (VI век) и др. Среди сохранившихся трудов в первую очередь следует назвать «Начала» Евклида и отдельные книги Аристотеля, Архимеда, Аполлония и Диофанта.
Начальный период
Вплоть до VI века до н. э. греческая математика ничем не выделялась. Были, как обычно, освоены счёт и измерение. Греческая нумерация (запись чисел), как позже римская, была аддитивной, то есть числовые значения цифр складывались. Первый её вариант (аттическая, или геродианова) содержали буквенные значки для 1, 5, 10, 50, 100 и 1000. Соответственно была устроена и счётная доска (абак) с камешками. Кстати, термин калькуляция (вычисление) происходит от calculus — камешек. Особый дырявый камешек обозначал нуль.
Позднее (начиная с V века до н. э.) вместо аттической нумерации была принята алфавитная — первые 9 букв греческого алфавита обозначали цифры от 1 до 9, следующие 9 букв — десятки, остальные — сотни. Чтобы не спутать числа и буквы, над числами рисовали чёрточку. Числа, большие 1000, записывали позиционно, помечая дополнительные разряды специальным штрихом (внизу слева). Специальные пометки позволяли изображать и числа, большие 10000.
В VI веке до н. э. начинается «греческое чудо»: появляются сразу две научные школы — ионийцы (Фалес Милетский, Анаксимен, Анаксимандр) и пифагорейцы. О достижениях ранних греческих математиков мы знаем в основном по упоминаниям позднейших авторов, преимущественно комментаторов Евклида, Платона и Аристотеля.
Фалес, богатый купец, хорошо изучил вавилонскую математику и астрономию — вероятно, во время торговых поездок. Ионийцы, по сообщению Евдема Родосского, дали первые доказательства нескольких простых геометрических теорем — например, о том, что вертикальные углы равны[4]. Однако главная роль в деле создания античной математики принадлежит пифагорейцам.
Пифагорейская школа
Пифагор, основатель школы — личность легендарная, и достоверность дошедших до нас сведений о нём проверить невозможно. Видимо, он, как и Фалес, много путешествовал и тоже учился у египетских и вавилонских мудрецов. Вернувшись около 530 г. до н. э. в Великую Грецию (район южной Италии), он в городе Кротон основал нечто вроде тайного духовного ордена. Именно он выдвинул тезис «Числа правят миром», и с исключительной энергией занимался его обоснованием. В начале V в. до н. э., после неудачного политического выступления, пифагорейцы были изгнаны из Южной Италии, и союз прекратил свое существование, однако популярность учения от рассеяния только возросла. Пифагорейские школы появились в Афинах, на островах и в греческих колониях, а их математические знания, строго оберегаемые от посторонних, сделались общим достоянием.
Рафаэль Санти. Пифагор (деталь Афинской школы)
Многие достижения, приписываемые Пифагору, вероятно, на самом деле являются заслугой его учеников. Пифагорейцы занимались астрономией, геометрией, арифметикой (теорией чисел), создали теорию музыки. Пифагор первый из европейцев понял значение аксиоматического метода, чётко выделяя базовые предположения (аксиомы, постулаты) и дедуктивно выводимые из них теоремы.
Геометрия пифагорейцев в основном ограничивалась планиметрией (судя по дошедшим до нас позднейшим трудам, очень полно изложенной) и завершалась доказательством «теоремы Пифагора». Хотя изучались и правильные многогранники.
Была построена математическая теория музыки. Зависимость музыкальной гармонии от отношений целых чисел (длин струн) была сильным аргументом пифагорейцев в пользу исконной математической гармонии мира, спустя 2000 лет воспетой Кеплером. Они были уверены, что «элементы чисел являются элементами всех вещей… и что весь мир в целом является гармонией и числом»[5]. В основе всех законов природы, полагали пифагорейцы, лежит арифметика, и с её помощью можно проникнуть во все тайны мира. В отличие от геометрии, арифметика у них строилась не на аксиоматической базе, свойства натуральных чисел считались самоочевидными, однако доказательства теорем и здесь проводили неуклонно. Понятия нуля и отрицательных чисел ещё не возникли.
Пифагорейцы далеко продвинулись в теории делимости, но чрезмерно увлеклись «треугольными», «квадратными», «совершенными» и т. п. числами, которым, судя по всему, придавали мистическое значение. Видимо, правила построения «пифагоровых троек» были открыты уже тогда; исчерпывающие формулы для них приводятся у Диофанта. Теория наибольших общих делителей и наименьших общих кратных тоже, видимо, пифагорейского происхождения. Они построили общую теорию дробей (понимаемых как отношения (пропорции), так как единица считалась неделимой), научились выполнять с дробями сравнение (приведением к общему знаменателю) и все 4 арифметические операции. Пифагорейцы знали, задолго до «Начал» Евклида, деление целых чисел с остатком и «алгоритм Евклида» для практического нахождения наибольшего общего делителя. Непрерывные дроби как самостоятельный объект выделили только в Новое время, хотя их неполные частные естественным путём получаются в алгоритме Евклида.
Первой трещиной в пифагорейской модели мира стало ими же полученное доказательство иррациональности 
Положение попытался спасти талантливый пифагореец Теэтет. Он (и позже Евдокс) предложили новое понимание числа, которое теперь формулировались на геометрическом языке, и проблем соизмеримости не возникало. Теэтет разработал также полную теорию делимости и классификацию иррациональностей. Повидимому, ему также были известны понятие простого числа и основная теорема арифметики[7].
Впоследствии, уже в Новое время, выяснилось, что построение числовой алгебры на основе геометрии было стратегической ошибкой пифагорейцев. Например, с точки зрения геометрии выражения 

Нумерологическая мистика пифагорейцев нередко приводила к произвольным и спекулятивным выводам. Например, они были уверены в существовании невидимой Антиземли, так как без неё число небесных сфер (нижнее небо, Солнце, Луна и 6 планет) не составляет совершенного числа 10. В целом, несмотря на обилие мистики и эксцентричных предрассудков, заслуги пифагорейцев в развитии и систематизации античных математических знаний неоценимы.
V век до н. э. — Зенон, Демокрит
В V веке до н. э. появились новые вызовы оптимизму пифагорейцев.
Первый из них — три классические задачи древности: удвоение куба, трисекция угла и квадратура круга. Греки строго придерживались требования: все геометрические построения должны выполняться с помощью циркуля и линейки, то есть с помощью совершенных линий — прямых и окружностей. Однако для перечисленных задач найти решение каноническими методами не удавалось. Алгебраически это означало, что не всякое число можно получить с помощью 4 арифметических операций и извлечения квадратного корня.
Квадратурой круга безуспешно занимался выдающийся геометр-пифагореец, автор доевклидовых «Начал», первого свода геометрических знаний, Гиппократ Хиосский.
Первые две задачи сводятся к кубическим уравнениям. Архимед позже дал общее решение кубических уравнений с помощью конических сечений. Однако многие комментаторы продолжали считать подобные методы неприемлемыми. Гиппий из Элиды (V век до н. э.) показал, что для трисекции угла полезна квадратриса (первая трансцендентная кривая в истории математики); она же, кстати, решает и задачу квадратуры круга (Динострат, IV век до н. э.).
Помимо перечисленных, греки активно исследовали задачу деления круга: какие правильные многоугольники можно построить циркулем и линейкой. Без труда удавалось разделить окружность на 3, 4, 5, 15 частей, а также удвоить перечисленные значения. Но семиугольник никому не поддавался. Как оказалось, здесь также получается кубическое уравнение. Полную теорию опубликовал только Гаусс в XIX веке.
Зенон Элейский
Второй удар по пифагореизму нанёс Зенон Элейский, предложив ещё одну тему для многовековых размышлений математиков. Он высказал более 40 парадоксов (апорий), из которых наиболее знамениты четыре. Вопреки многократным попыткам их опровергнуть и даже осмеять, они, тем не менее, до сих пор служат предметом серьёзного анализа. Здесь затронуты самые деликатные вопросы оснований математики — конечность и бесконечность, непрерывность и дискретность. Математика тогда считалась средством познания реальности, и суть споров можно было выразить как неадекватность непрерывной, бесконечно делимой математической модели физически дискретной материи[8].
В конце V века до н. э. жил ещё один выдающийся мыслитель — Демокрит. Он знаменит не только созданием концепции атомов. Архимед писал, что Демокрит нашёл объём пирамиды и конуса, но доказательств своих формул не дал. Вероятно, Архимед имел в виду доказательство методом исчерпывания, которого тогда ещё не существовало.
IV век до н. э. — Платон, Евдокс
Рафаэль Санти. Афинская школа
Уже к началу IV века до н. э. греческая математика далеко опередила всех своих учителей, и её бурное развитие продолжалось. В 389 году до н. э. Платон основывает в Афинах свою школу — знаменитую Академию. Математиков, присоединившихся к Академии, можно разделить на две группы: на тех, кто получил своё математическое образование вне Академии, и на учеников Академии. К числу первых принадлежали Теэтет Афинский, Архит Тарентский и позднее Евдокс Книдский; к числу вторых — братья Менехм и Динострат.
Сам Платон конкретных математических исследований не вёл, но опубликовал глубокие рассуждения по философии и методологии математики. А ученик Платона, Аристотель, оставил бесценные для нас записки по истории математики.
Евдокс Книдский первый создал геоцентрическую модель движения светил с 27 сферами. Позже эта конструкция была развита Аполлонием, Гиппархом и Птолемеем, которые увеличили число сфер до 34 и ввели эпициклы. Ему же принадлежат два выдающихся открытия: общая теория отношений (геометрическая модель вещественных чисел) и античный анализ — метод исчерпывания.
III век до н. э. — Евклид, Архимед, Аполлоний
Евклид. Оксфордский университетский музей естественной истории
После завоеваний Александра Македонского научным центром древнего мира становится Александрия Египетская. Птолемей I основал в ней Мусейон (Дом Муз) и пригласил туда виднейших учёных. Это была первая в грекоязычном мире государственная академия, с богатейшей библиотекой (ядром которой послужила библиотека Аристотеля), которая к I веку до н. э. насчитывала 70000 томов.
Учёные Александрии объединили вычислительную мощь и древние знания вавилонских и египетских математиков с научными моделями эллинов. Значительно продвинулись плоская и сферическая тригонометрия, статика и гидростатика, оптика, музыка и др. Эратосфен уточнил длину меридиана и изобрёл своё знаменитое «решето». В истории математики известны три великих геометра древности, и прежде всего — Евклид с его «Началами». Тринадцать книг Начал — основа античной математики, итог её 300-летнего развития и база для дальнейших исследований. Влияние и авторитет этой книги были огромны в течение двух тысяч лет.
Фундамент математики, описанный Евклидом, расширил другой великий учёный — Архимед, один из немногих математиков античности, которые одинаково охотно занимались и теоретической, и прикладной наукой. Он, в частности, развив метод исчерпывания, сумел вычислить площади и объёмы многочисленных фигур и тел, ранее не поддававшихся усилиям математиков.
Последним из тройки великих был Аполлоний Пергский, автор глубокого исследования конических сечений.
Упадок античной науки
После Аполлония (со II века до н. э.) в античной науке начался спад. Новых глубоких идей не появляется. В 146 году до н. э. Рим захватывает Грецию, а в 31 году до н. э. — Александрию.
Среди немногочисленных достижений:
- открытие конхоиды (Никомед);
- известная формула Герона для площади треугольника (I век н. э.);
- содержательное исследование сферической геометрии Менелаем Александрийским;
- завершение геоцентрической модели мира Птолемея (II век н. э.), для чего потребовалась глубокая разработка плоской и сферической тригонометрии.
Необходимо отметить деятельность Паппа Александрийского (III век). Только благодаря ему до нас дошли сведения об античных учёных и их трудах.
На фоне общего застоя и упадка резко выделяется гигантская фигура Диофанта — последнего из великих античных математиков, «отца алгебры».
После III века н. э. александрийская школа просуществовала около 100 лет — приход христианства и частые смуты в империи резко снизили интерес к науке. Отдельные учёные труды ещё появляются в Афинах, но в 529 году Юстиниан закрыл Афинскую академию как рассадник язычества.
Часть учёных переехала в Персию или Сирию и продолжала труды там. От них уцелевшие сокровища античного знания получили учёные стран ислама (см. Математика исламского средневековья).
Заключение
Греческая математика поражает прежде всего красотой и богатством содержания. Многие учёные Нового времени отмечали, что мотивы своих открытий почерпнули у древних. Зачатки анализа заметны у Архимеда, корни алгебры — у Диофанта, аналитическая геометрия — у Аполлония и т. д. Но главное даже не в этом. Два достижения греческой математики далеко пережили своих творцов[9].
Первое — греки построили математику как целостную науку с собственной методологией, основанной на чётко сформулированных законах логики.
Второе — они провозгласили, что законы природы постижимы для человеческого разума, и математические модели — ключ к их познанию.
В этих двух отношениях античная математика вполне современна.
Литература
- Башмакова И. Г. Лекции по истории математики в Древней Греции. // Историко-математические исследования. — М.: Физматгиз, 1958. — № 11. — С. 225-440.
- Ван дер Варден. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. М.: Физматгиз, 1959, 456 с.
- Выгодский М. Я. Арифметика и алгебра в древнем мире. М., 1967.
- Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — 376 с.
- Депман И. Я. История арифметики. Пособие для учителей. Изд.второе. М.: Просвещение, 1965.
- История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
- Клайн М. Математика. Утрата определённости. М., Мир, 1984.
- Нейгебауэр О. Точные науки в древности. М., 1968.
- Розенфельд Б. А. Аполлоний Пергский. (2004)
- Рыбников К. А. История математики. М., 1994.
- Хрестоматия по истории математики. Арифметика и алгебра. Теория чисел. Геометрия. Под ред. А. П. Юшкевича. М., 1976.
Ссылки
- Математика // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.
Примечания
- ↑ Петров Ю. П. История и философия науки. Математика, вычислительная техника, информатика. Спб.: БХВ-Петербург, 2005. ISBN 5-94157-689-7, 448 с., стр. 9.
- ↑ Башмакова И. Г., 1958, с. 232.
- ↑ Шмутцер Э., Шютц В. Галилео Галилей. — М.: Мир, 1987. — С. 116. — 140 с.
- ↑ Башмакова И. Г., 1958, с. 240.
- ↑ Аристотель. Метафизика. Перевод и примечания А. В. Кубицкого. М.—Л., 1934, стр. 26—27.
- ↑ Аристотель. Метафизика. Перевод и примечания А. В. Кубицкого. М.—Л., 1934, стр. 22.
- ↑ Башмакова И. Г., 1958, с. 260.
- ↑ См. подробнее Апории Зенона#Современная трактовка.
- ↑ Башмакова И. Г., 1958, с. 436-437.
| |
|
|---|---|
| Страны и эпохи |
Древний Египет • Вавилон • Древний Китай • Древняя Греция • Индия • Страны ислама • Империя инков • Россия |
| Тематические разделы |
Алгебра • Аналитическая геометрия • Арифметика • Геометрия • Дифференциальная геометрия и топология • Комбинаторика • Криптография • Линейная алгебра • Логарифмы • Математический анализ • Неевклидова геометрия • Теория вероятностей • Теория множеств • Топология • Тригонометрия • Функциональный анализ |
| См. также |
Бесконечно малые • Вещественные числа • Иррациональные числа • Комплексные числа • Математические обозначения • Непрерывные дроби • Отрицательные числа • Функции |
|
п • о • р Древняя Греция в темах — Портал:Греция |
|
|---|---|
| История |
Доисторическая Греция · Эгейская цивилизация (Западноанатолийская · Минойская · Кикладская · Элладская · Микенская) · Греческие Тёмные века · Архаическая Греция · Классическая Греция · Эллинистическая Греция · Римская Греция |
| Древние греки |
Догреческий субстрат · Лелеги · Пеласги · Ионийцы · Ахейцы · Эолийцы · Дорийцы · Дорийское вторжение · Эллинское происхождение древних македонцев |
| География |
Эгейское море · Геллеспонт · Македония · Спарта · Афины · Коринф · Фивы · Антиохия · Александрия · Пергам · Милет · Эфес · Дельфы · Делос · Олимпия · Троя · Родос · Крит · Пелопоннес · Микены · Эпир · Кипр · Великая Греция · Колонии Древней Греции |
| Правители |
Цари Афин и Аттики · Архонты Афин · Цари Спарты · Пирриды · Македонские цари · Цари Аркадии · Цари Аргоса · Цари Коринфа · Правители Сиракуз · Эпитиды · Правители Лидии · Атталиды · Диадохи · Цари Коммагены · Понтийские цари · Правители Дакии |
| Политика |
Демократия · Апелла · Экклесия · Дикастерий · Совет пятисот · Агора · Graphē paranómōn · Ареопаг · Коринфский союз · Диадохи |
| Войны |
Войны · Армия Древней Македонии · Армия Спарты · Гоплит · Гетайры · Пельтасты · Фаланга · Сариса · Священный отряд из Фив · Спартанские всадники |
| Экономика и право |
Деньги и монеты · Сельское хозяйство · Рабство · Право |
| Культура |
Религия и Мифология · Философия · Литература · Одежда · Кухня · Вина · Образование · Олимпийские соревнования · Проституция · Гомосексуальность |
| Архитектура |
Парфенон · Храм Артемиды Эфесской · Афинский Акрополь · Афинская агора · Храм Зевса · Храм Гефеста · Храмовый комплекс Самофракии |
| Искусство |
Архитектура · Чеканка монет · Литература · Музыка · Керамика · Скульптура · Театр |
| Наука |
Календари · Картография · Астрономия · Математика · Медицина · Технологии |
| Язык и письмо |
Протогреческий * Микенский * Гомеровский * Диалекты (эолийский * аркадо-кипрский * аттический * дорийский * ионийский * локридский * древнемакедонский язык * памфилийский) * Койне * Линейное письмо А * Линейное письмо Б * Греческий алфавит |
В
XI-IX
вв. до н.э. на территории Греции происходит
переход от первобытнообщинного строя
к рабовладельческому. В VIII-VI
вв. до н.э. там устанавливается
рабовладельческий строй и образуются
города-государства.
Помимо
материковой части Греции, расположенной
на Балканском полуострове, многочисленных
островов и побережья Малой Азии (нынешней
Турции), греки с давних пор стали заселять
и другие земли, в том числе берега Черного
и Азовского морей. Много греческих
колоний было на побережье Италии.
В
VI
l
в. до н.э. в результате народных восстаний
в большинстве греческих городов
господство рабовладельческой аристократии
сменяется правление народа – демократией,
конечно, ограниченной, рабовладельческой.
В Vв.
до н.э. греческие города, объединившись
вокруг Афин, отразили нашествие страшного
врага – Персии. Большая часть Vв.
до н.э. – это золотой век Афин, они
становятся политическим и культурным
центром Греции. За короткий срок греки
добились больших успехов в науках:
математике, механике, философии,
астрономии; в искусстве: скульптуре,
живописи, архитектуре; создали
замечательные произведения литературы
(мифы, трагедии и комедии, поэмы Гомера
“Илиада” и “Одиссея”), театр, начали
проводить олимпийские игры.
Культура,
наука и искусство древней Греции
представляют собой уникальное явление
в истории. Почему же небольшой народ за
сравнительно короткое время достиг
поразительных результатов в этих
областях? Главная причина заключалась
в демократическом правлении. Значительная
часть свободного населения имела
возможность участвовать в развитии
культуры, науки и искусства. Важные и
спорные вопросы решались на народных
собраниях и в судах. Там и тут нужно было
уметь тщательно аргументировать,
доказывать свою точку зрения и убедительно
опровергать аргументы противника, в
частности, приводя их к нелепости. Отсюда
в науку, в первую очередь в математику
проникло доказательство: например,
отсюда происходит метод доказательства
от противного. Другая причина –
географическое положение Греции. Греки
были вынуждены издавна заниматься
мореплавание и кораблестроением: это
было необходимо для связи между городами,
зачастую отделенными друг от друга
большим расстоянием по морю, и, в
частности, для торговли, поскольку
греческие города многие предметы
потребления могли получать только из
других городов или даже из других стран.
Для нужд мореплавания и кораблестроения
приходилось развивать строительное
дело, механику, астрономию и математику.
Связи греческих городов с соседними
странами давали грекам возможность
познакомиться с культурными и научными
достижениями соседей.
1.Письменность
в Греции появилась в IX-VIII
вв. до н.э. Писали в Греции на папирусе,
глиняных черепках и на дощечках, покрытых
воском. Позднее наиболее значительные
литературные и научные сочинения стали
писать и на пергаменте – тщательно
обработанной коже телят и ягнят.
Первая
греческая нумерация была изобретена в
VIII-VII
вв. до н.э. в Аттике (полуостров в Средней
Греции, на котором расположены Афины)
и поэтому называлась аттической. Вот
примеры записи натуральных чисел по
этой системе (рис.3):
Рис.3
Буквы
Г, ∆, Н, Х, М — это начальные буквы греческих
слов для чисел 5, 10, 100, 1000, 10000. Отсюда
видно, что система счисления была
десятичной непозиционной. Она далеко
уступала вавилонской и была неудобна
для письменных вычислений. Поэтому
греки считала, в основном, на абаке. Абак
представлял собой доску, разграфленную
на колонки; в эти колонки раскладывались
камешки по разрядному принципу.
Аттическая
нумерация оказала влияние на римскую,
созданную по ее образцу позднее. Абак
также применялся в Риме в качестве
основного инструмента счета, а в средние
века – в большинстве государств Западной
Европы.
Позднее,
в IV-III
вв. до н.э., эта нумерация у греков
сменилась новой — ионийской (Иония –
область на побережье малой Азии).
Рассмотрим примеры записи чисел по этой
системе (рис.4).

Рис.
4
Ионийская
система счисления была десятичной
непозиционной. В ней последовательные
буквы греческого алфавита использовались
для обозначения единиц от 1 до 9, десятков
от 10 до 90 и сотен от 100 до 900. На числе 900
все буквы алфавита (включая три устаревшие,
специально сохранившиеся для нумерации)
исчерпывались.
Вот
как записывались тысячи и десятки тысяч:

.
Подобная
система счисления называется алфавитной.
В истории известны еще несколько
алфавитных систем: например, такова
церковно-славянская нумерация,
составленная по образцу греческой.
Вот
примеры записи дробных чисел:
Последняя
запись применялась только к дробям с
числителем 1
2.
Первой научной школой древней Греции
была ионийская
школа,
существовавшая в VI
в. До н.э. в Ионии. Основателем ее был
Фалес Милетский, которого греки считали
отцом греческой науки. Сам Фалес был
философом, математиком и астрономом, а
его школа была естественно−
−научной
и философской. Ионийцы в философии были
наивными материалистами: они пытались
объяснить мир, исходя из единого
материального начала. Так, сам Фалес
считал первоосновой мира воду.
Математикой
в ионийской школе записался в первую
очередь сам Фалес. Его заслуга в этой
области состоит в том, что он явно ввел
в математику доказательство. Ионийцы
первыми в Греции занялись геометрией
как наукой.
Фалес
доказал следующие теоремы:
1)
о равенстве вертикальных углов;
2)
о том, что диаметр круга делит круг
пополам;
3)
о равенстве углов при основании
равнобедренного треугольника
4)
о равенстве двух треугольников, имеющих
равными сторону и два прилегающих угла;
5)
о пересечении сторон угла параллельными
прямыми (школьная теорема Фалеса) и др.
Сами доказательства до нас не дошли.
3.Второй
научной школой древней Греции, более
крупной и уделявшей гораздо большее
внимание математике, чем у ионийцев,
была школа Пифагора.
Она возникла в том же VI
в. до н.э., но позже школы Фалеса.
Пифагор
Самосский – крупнейший ученый VI
в. до н.э. Он родился на острове Самос,
много лет провел в Египте и Вавилоне.
По возвращении в Грецию он переехал в
город Кротон, греческую колонию на юге
Италии, и основал там пифагорейское
братство. Братство было не только научной
школой, но и политическим союзом.
В
братство принимались только аристократы.
Вступивший в него должен был пожертвовать
все свое имущество братству и проходил
довольно длительный и сложный образ
испытаний и посвящения; например, в
течение двух лет он должен был хранить
молчание. Деятельность союза держалась
в тайне, а все научные открытия пифагорейцев
приписывались “учителю” – Пифагору.
В
философии пифагорейцы были идеалистами.
Они считали, что в основе мира лежит
идея числа (натурального), и по этой
причине изучали свойства натуральных
чисел. Пифагорейцы произвели коренное
преобразование математики того времени,
которая тогда сводилась к арифметике
(теории чисел) и геометрии. Кроме того,
они занимались гармонией (математической
теорией музыки) и астрономией.
В
системе взглядов пифагорейцев на мир
было много мистики и суеверий. Например,
четные числа они называли женскими,
нечетные – мужскими, а сумма первого
женского числа 2 и первого мужского 3 (1
не относили к числам, поскольку под
числом понимали множество единиц), т.е.
число 5, считалась символом брака.
Пятиконечная звезда, образованная
диагоналями правильного пятиугольника,
считалась символом здоровья; она служила
опознавательным знаком пифагорейцев.
Пифагорейцы
приняли участие в политической борьбе,
и это оказалось губительным для них.
Братство было разгромлено. После смерти
учителя научные открытия пифагорейцев,
которые до этого держались в тайне,
получили широкую известность благодаря
тому, что многие пифагорейцы вынуждены
были зарабатывать себе на жизнь уроками,
которые они давали гражданам. Письменных
научных сочинений у пифагорейцев,
по-видимому, не было, и мы догадываемся
об их математических знаниях только по
косвенным признакам, в передаче греческих
ученых и историков последующих лет.
Рассмотрим
открытия пифагорейцев в арифметике и
теории чисел. Они впервые ввели четные
и нечетные числа и изучили их свойства,
ввели простые и составные числа. Они
изучили треугольные числа – числа вида
квадратные
числа —
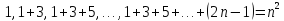
пятиугольные
числа – числа вида
Названия
объясняются тем, что эти числа изображались
геометрически с помощью вершин правильного
треугольника, квадрата и правильного
пятиугольника (рисунки 5-7).
Пифагорейцы
ввели совершенные числа: это числа,
равные сумме всех своих делителей
(исключая делитель, равный самому числу);
например,
Они
изучали различные свойства дробей, но
при этом считали дроби не числами, а
чем-то вспомогательным. Отношения
натуральных чисел приходилось
рассматривать при измерении длин
отрезков и при изучении подобия фигур.
Перейдем
к геометрии. По-видимому, пифагорейцы
впервые изложили в систематическом
виде почти всю планиметрию. Они
сформулировали некоторые аксиомы
геометрии. Вершиной планиметрии считалась
теорема Пифагора, которая впервые была
доказана пифагорейцами. Что касается
стереометрии, то здесь пифагорейцы
сделали значительно меньше.
Два
открытия школы Пифагора находятся на
стыке геометрии и арифметики. Это,
во-первых, формулы для длин сторон
пифагоровых треугольников
где
— нечетное число, большее 1. Они не
охватывают всех случаев в отличие от
формул, применявшихся в Вавилоне, так
как пригодны лишь для таких прямоугольных
треугольников, у которых длина гипотенузы
больше длины одного из катетов на
Другое
открытие – доказательство несоизмеримости
диагонали квадрата с его стороной с
помощью предложения о том, что не
существует рационального числа, квадрат
которого равен 2. Доказательство
последнего утверждения, вероятно,
проводилось так же, как и в наши дни
(см., например, учебник “Алгебра-8” под
ред. С.А. Теляковского). Это открытие
было большой неприятностью для
пифагорейцев: ведь они считали, что все
в мире можно выразить натуральным числом
или отношением двух натуральных чисел,
а тут оказалось, что длина диагонали
единичного квадрата, которая по теореме
Пифагора удовлетворяет условию

не может быть выражена подобным образом.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Математика – одна из древнейших, важнейших и
сложнейших компонентов человеческой культуры.
История математики тысячами нитей связана с
историей других наук. Народная мудрость гласит,
что невозможно понять подлинный смысл
настоящего и цели будущего, если не знать и не
ценить прошлое. Жизнь не стояла на месте. С
развитием человечества появляется потребность
передавать известия друг другу, писать, считать.
Так в далёком прошлом постепенно зарождалась
математика. Древние греки были удивительно
талантливым народом, у которого есть чему
поучиться даже сейчас. В те времена Греция
состояла из многих мелких государств. Каждый раз,
когда приходилось решать какой-нибудь важный
государственный вопрос, горожане собирались на
площади, обсуждали его, спорили, а потом
голосовали. Они были хорошими «спорщиками».
По преданию, в то время сложилось утверждение:
» В споре рождается истина!» Греки
отличались трудолюбием и смелостью. Среди них
были отличные строители, мореплаватели, купцы и
художники. Они внесли большой вклад в развитие
культуры и науки, особенно математики. Истории
известно что ученые-математики древней Греции
были крупнейшими математиками в далеком прошлом
и задачи, составленные ими интересны и в наши дни.
Весьма большая часть нашего современного
школьного курса математики, особенно геометрии,
была известна древним грекам. Учитель никогда не
начнет изложения новой темы, не говоря о новом
разделе математики, без вводной исторической
части, вызывающей интерес и внимание учеников.
Уроки с привлечением исторического материала
никого не оставляют равнодушными. Как, знакомя
учеников с начальными понятиями геометрии 7
класса, не рассказать о греческой
математике?..Как изучая тему “Площадь” 8 кл. не
объяснить измерение площадей в Древней Греции
(решение старинных задач). Именно здесь так
устанавливается связь исторических сведений с
материалом рассматриваемой темы. История
математики выступает средством активизации
познавательной деятельности учащихся. А это
является основой учебной деятельности по той
причине, что:
– интерес способствует формированию глубоких
и прочных знаний;
– развивает и повышает качество мыслительной
деятельности, активность в учении,
благоприятствует формированию способностей;
– создает более благоприятный эмоциональный
фон для протекания всех психических процессов.
Экскурс в историю можно сопровождать
картинками, слайдами, презентацией. Математика
со времени её зарождения как науки и много раньше
была тесно связана не только с цивилизацией, с
практикой, но и со всей общечеловеческой
культурой – со всем миром. И математические
теории, и методы открывались, создавались
конкретными личностями, математиками, жизнь и
судьба которых, интересная и насыщенная,
поучительная и порой трагическая, неотделима от
исторической эпохи, в которую они творили.
Ученые Греции
Расскажем о Пифагоре, именем которого названа
теорема, которую знают все. В Древней Греции жил
ученый Пифагор (родился он около 580 г. до н. э.,
а умер в 500 г. до н. э.). О жизни этого ученого
известно немного, зато с его именем связано ряд
легенд. Рассказывают, что он много путешествовал,
был в Индии, Египте, Вавилоне, изучал древнюю
культуру и достижения науки разных стран.
Вернувшись на родину, Пифагор организовал кружок
молодежи из представителей аристократии. В
кружок принимались с большими церемониями после
долгих испытаний. Каждый вступающий отрекался от
своего имущества и давал клятву хранить в тайне
учения основателя. Так на юге Италии, которая
была тогда греческой колонией, возникла так
называемая пифагорейская школа. Пифагорейцы
занимались математикой, философией,
естественными науками. Ими было сделано много
важных открытий в арифметике и геометрии. В школе
существовал декрет, по которому авторство всех
математических работ приписывалось Пифагору.
Пифагор был убит в уличной схватке во время
народного восстания. После его смерти ученики
окружили имя своего учителя множеством легенд,
так что установить о Пифагоре правду невозможно.
Теорема Пифагора имеет богатую историю.
Оказывается, она задолго до Пифагора была
известна египтянам, вавилонянам, китайцам и
индийцам. Доказательство самого Пифагора до нас
не дошло. В настоящее время имеется свыше 100
доказательств. Возможно, что одно из них
принадлежит Пифагору и его ученикам.
Архимед – вершина научной мысли древнего
мира. Архимед родился в 287 году до нашей эры в
греческом городе Сиракузы, где и прожил почти всю
свою жизнь. Отцом его был Фидий, придворный
астроном правителя города Герона. Учился Архимед
в Александрии, где правители Египта Птолемеи
собрали лучших греческих ученых и мыслителей, а
также основали самую большую в мире библиотеку.
Основные работы Архимеда касались различных
практических приложений математики, физики,
гидростатики и механики. В сочинении «Параболы
квадратуры» Архимед обосновал метод расчета
площади параболического сегмента, причем сделал
это за две тысячи лет до открытия интегрального
исчисления. В труде «Об измерении круга»
Архимед впервые вычислил число «пи» –
отношение длины окружности к диаметру – и
доказал, что оно одинаково для любого круга.
Архимед, погибший при захвате римлянами его
родного города Сиракузы в то время, когда пришел
римский солдат. По преданию, Архимед был увлечен
решением геометрической задачи, чертеж которой
был выполнен на песке. Солдат, убивший Архимеда,
или не знал о приказе военачальника сохранить
жизнь Архимеду, или не узнал Архимеда. В наше
время имя Архимеда связывают главным образом с
его замечательными математическими работами,
однако в античности он прославился также как
изобретатель различного рода механических
устройств и инструментов, о чем сообщают авторы,
жившие в более позднюю эпоху. Считается, что
Архимед был изобретателем т.н. архимедова винта,
который служил для подъема воды на поля и явился
прообразом корабельных и воздушных винтов.
- Вызывает сомнение и подлинность истории, что
будто бы царь поручил Архимеду проверить, из
чистого ли золота сделана его корона или же
ювелир присвоил часть золота, сплавив его с
серебром. “Размышляя над этой задачей, Архимед
как-то зашел в баню и там, погрузившись в ванну,
заметил, что количество воды, переливающейся
через край, равно количеству воды, вытесненной
его телом. Это наблюдение подсказало Архимеду
решение задачи о короне, и он, не медля ни секунды,
выскочил из ванны и, как был нагой, бросился
домой, крича во весь голос о своем открытии:
“Эврика! Эврика!” (греч. “Нашел! Нашел!”)”. - При обороне Сиракуз от осаждавших этот город
римских войск Архимед создал подъемные и
метательные машины, а “зажигательное зеркало”,
с помощью которого он якобы сжег корабли доныне
остается загадкой, волнующей умы исследователей. - Сохранившиеся математические сочинения
Архимеда можно разделить на три группы.
Сочинения первой группы посвящены в основном
доказательству теорем о площадях и объемах
криволинейных фигур или тел. Сюда относятся
трактаты “ О шаре и цилиндре, Об измерении круга,
О коноидах и сфероидах, О спиралях и О квадратуре
параболы”. Вторую группу составляют работы по
геометрическому анализу статических и
гидростатических задач: О равновесии плоских
фигур, О плавающих телах. К третьей группе можно
отнести различные математические работы: О
методе механического доказательства теорем,
Исчисление песчинок, Задача о быках и
сохранившийся лишь в отрывках Стомахион.
Евклид. Древнегреческий ученый Евклиду
принадлежат сочинения по механике, оптике,
музыке. Известны его заслуги и в астрономии.
Евклиду приписываются также несколько теорем и
новых доказательств
Из дошедших до нас сочинений Евклида наиболее
знамениты “Начала”, состоящие из 15 книг. В 1-й
книге формулируются исходные положения
геометрии, а также содержатся основополагающие
теоремы планиметрии, среди которых теорема о
сумме углов треугольника и теорема Пифагора. При
построении правильных многоугольников опять
звучит это имя Евклида. XIII книга «Начал»
посвящена платоновым телам – правильным
многогранникам, красотой которых восхищаемся на
уроках стереометрии. Рассматривая вопросы
дифференциального и интегрального исчислений на
уроках анализа, говорим о том, что идеи,
положенные в их основу Ньютоном и Лейбницем в XVII
в., уходят своими корнями к методу исчерпывания,
открытому еще Евклидом и Архимедом.
Фалес из Милета (ок.625 – ок.547 до н.э.)
древнегреческий ученый и государственный
деятель, первый из семи мудрецов. Во время
путешествий он посетил Египет, где и
познакомился с астрономией и геометрией. Легенда
рассказывает о том, что Фалес привел в изумление
египетского царя Амазиса, измерив высоту одной
из пирамид по величине отбрасываемой ею тени
Задача. Измерить высоту пирамиды по
отбрасываемой ею тени. (Размеры даны в локтях; 1
локоть = 7 ладоням = 466 мм.)
Зачинатель и родоначальник греческой
философии и науки. Считается, что Фалес первым
доказал несколько геометрических теорем, а
именно:
- вертикальные углы равны;
- треугольники с равной одной стороной и равными
углами, прилегающими к ней, равны; - углы при основании равнобедренного
треугольника равны; - диаметр делит круг пополам;
- угол, вписанный в полуокружность, всегда будет
прямым.
Фалес определял высоту предмета по его тени,
расстояния до кораблей, используя подобие
треугольников.
Он сделал ряд открытий в области астрономии,
установил время равноденствий и солнцестояний,
Определил продолжительность года. Фалес был
причислен к группе “семи мудрецов”.
Эратосфен Киренский (ок. 276 – 194 до н.э.) –
разносторонний ученый: математик, астроном,
географ, историк и филолог. Прославился
благодаря изобретению “решета Эратосфена”. В
сочинении “ Решето” Эратосфен создал
оригинальный метод для “отсеивания” простых
чисел. В последовательности натуральных чисел
зачеркнем 1. Число 2-простое. Зачеркнём все числа,
кратные 2. Число 3– первое из незачеркнутых –
простое. Затем зачеркнем всякое число,
делящееся на 3, и т. д. Так можно получить сколь
угодно большой фрагмент последовательности
простых чисел. Во времена Эратосфена писали на
восковых дощечках. Числа не зачёркивали, а
прокалывали. Отсюда и название метода– решето.
Сконструировал прибор – мезолябий для
механического решения делосской задачи
(удвоения куба).
Осуществил первое измерение размеров земли.
Измерив длину 1/50 дуги земного меридиана,
Эратосфен вычислил окружность земного шара и
получил 25 200 стадий, или 39 960 км, что лишь на 319 км
меньше действительного значения.
Герон Александрийский великий физик,
математик, механик и инженер древней Греции. Жил
предположительно в I-II века до нашей эры в
Александрии Египетской. Время жизни отнесено ко
второй половине первого века н. э. на том
основании, что он приводит в качестве примера
лунное затмение 13 марта 62 г. н. э.
Герона относят к величайшим инженерам за всю
историю человечества. Он первым изобрёл
автоматические двери, автоматический театр
кукол, автомат для продаж, скорострельный
самозаряжающийся арбалет, паровую турбину,
автоматические декорации, прибор для измерения
протяженности дорог (древний “таксометр”) и др.
Первым начал создавать программируемые
устройства (вал со штырьками с намотанной на него
веревкой).Одной из главных заслуг Герона
Александрийского перед историей, являются книги,
написанные им. В них описываются не только
собственные изобретения Герона, но и знания
других ученых древней Греции. Много работ Герона
Александрийского было посвящено Математике.
Больше всего в его работах формул по геометрии,
задач по вычислению геометрических фигур. Так же
здесь описывается и знаменитая формула Герона, с
помощью которой можно вычислить площадь
треугольника по трем сторонам.
В конце II в. н.э. начинается закат греческой
математики.
На фоне общего застоя и упадка резко выделяется
гигантская фигура Диофанта.
В III–IV веках нашей эры жил в городе Александрии
знаменитый греческий математик Диофант. Почти
все математики древности занимались
уравнениями. Много внимания им уделял, а главное,
много нового внес в способы их решения
древнегреческий ученый Диофант.
О Диофанте известно очень мало. Есть основание
полагать, что он жил около III в. н.э. Одна группа
уравнений, так называемые неопределенные
уравнения, до сих пор называются диофантовыми
уравнениями. Именно для них он нашел способ
решения.
Скудные сведения о Диофанте может дополнить
нам лишь надпись на надгробном камне,
сформулированная задаДо нас дошли шесть из
тринадцати книг “Арифметики”, написанных
Диофантом, да предание о надписи на его могильном
камне. Эта надпись дает возможность определить
продолжительность жизни математика, которого
позднее назвали “отцом греческой алгебры”.
Здесь погребен Диофант, и камень
могильный
При счете искусном расскажет нам,
Сколь долог был его век.
Велением бога он мальчиком был шестую часть
своей жизни;
В двенадцатой части затем прошла его светлая
юность.
Седьмую часть жизни прибавим – перед нами очаг
Гименея.
Пять лет протекли; и прислал Гименей ему сына.
Но горе ребенку! Едва половину он прожил
Тех лет, что отец, как скончался несчастный.
Четыре года страдал Диофант от утраты такой
тяжелой
И умер, прожив для науки. Скажи мне,
Скольких лет достигнув, смерть воспринял
Диофант?
Главный труд Диофанта– “Арифметика”, по
предположению, состоит из 13 книг. Книга Диофанта
“Арифметика” содержала большое количество
интересных задач, её изучали математики всех
поколений. Книга сохранилась до наших дней. В
честь Диофанта назван кратер на Луне.О жизни
Метродора, составителя задачи о жизни Диофанта,
ничего неизвестно, нет сведений о времени его
жизни и смерти. В историю математики древней
Греции он вошел как автор задач, составленных в
стихах. Задачи Метродора входили в рукописные
сборники и имели в своё время большое
распространение
Нет сомнений в научности математики Древней
Греции. Ни один народ древности не сделал столько
для развития математики, как жители Греции.
Человеческой природе свойственно уважение к
прошлому. Это уважение иногда вызывает у
учащихся желание взглянуть на математику как на
науку сквозь туман старины, прикоснутся к седой
древности, тысячелетним тайнам и загадкам…
Пускай останется извечный мир загадок
Чтоб продолжалась жизнь, не ведая конца.
В. Рождественнский
ПРЕЗЕНТАЦИЯ
Список используемой литературы
- Виленкин Н.Я. и др. За страницами учебника
математики. М. “Просвещение” АО “Учебная
литература” 1996. - Глейзер Г.И. История математики в школе. М.
“Просвещение” 1995. - Савин А.П. Энциклопедический словарь юного
математика. М. “Просвещение” 1995. - Чистяков В. Д. Старинные задачи по элементарной
математике. – Минск: вышэйшая школа, 1978. - Барвин И. И., Фрибус Е. А. Старинные задачи. Книга
для учащихся. – М.: Просвещение,199 - 3. Болгарский Б.В. Очерки по истории математики.
-2-е иэд., Выш.школа,1979. - Крыситский В. Шеренга великих математиков –
Варшава: Наша Ксенгарня, 1981. - Рыбников К.А. История математики – М.:
Просвещение, 1994. – 123 – 125 с.
Пифагор Самосский (около 570–490 гг. до н. э.) – один из самых известных древнегреческих философов, мистиков и математиков, создатель религиозно-философской школы. Будучи мудрым учителем, обучал людей различным наукам: математике, медицине, политической деятельности. Внёс весомый вклад в геометрию: всем школьникам известна теорема Пифагора.
Материал подготовлен совместно с учителем высшей категории
Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Философская школа
Свидетельства указывают на то, что после всех своих скитаний Пифагор осел в Кротоне (Южная Италия). Там он основал философскую школу, больше похожую на некий религиозный орден (последователи Пифагора считали возможным переселение души и реинкарнацию; считали, что человек должен благими делами заслужить место в мире Богов, а пока этого не произойдёт, душа так и будет возвращаться на Землю, «вселяясь» в тело животного или человека), где пропагандировались не только знания, но и особый образ жизни.
Именно Пифагор и его ученики, у которых авторитет учителя был непререкаем, ввели в обращение слова «философия» и «философ». Этот орден фактически пришел в Кротоне к власти, но по причине распространения антипифагорейских настроений, философ был вынужден уехать в город Метапонт, где и умер, приблизительно в 491 году до н.э.
Семья и юность
Точную дату рождения Пифагора определить невозможно, судить о ней и о его жизни в целом можно лишь по рукописным источникам об учениях философа, самый ранний из которых появился лишь через 200 лет после его смерти. Предполагается, что Пифагор родился примерно в 570 до н. э. на греческом острове Самос. Папа, его звали Мнесарх, был камнерезом. Мама носила имя Партенида. Известно, что она была из благородной семьи, предок которой основал греческую колонию на Самосе.
Плен в Вавилоне
Согласно одной из легенд, когда Пифагору исполнилось 18 лет, он покинул родной дом и отправился в Египет, чтобы набраться мудрости у местных жрецов. Там будущий философ изучал медицину и математику на протяжении 20 лет. Потом его взял в плен персидский властитель Камбис и увёл в Вавилон. В качестве узника Пифагор провёл ещё 12 лет, часто взаимодействуя с магами, и лишь потом вернулся на родной Самос. Уже в тот период местные жители признали 56-летнего Пифагора самым мудрым человеком в мире.
Вернувшись на родину, Пифагор стал преподавать свои идеи и учения. Вскоре о нём заговорила вся Греция. Люди с разных уголков страны съезжались на Самос, чтобы только увидеть и услышать мудрейшего философа. Со временем Пифагора стали привлекать к общественным делам. Утомившись от повышенного внимания и удручавшей его работы, он снова покидает остров и отправляется в Южную Италию.
Открытия
Именно Пифагору, как считают большинство исследователей, принадлежит открытие известной теоремы о том, что квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов.
Вечным оппонентом Пифагора был Гераклит, который считал, что «многознание» не есть признак настоящего философского ума. Аристотель никогда не цитировал Пифагора в своих трудах, а вот Платон считал Пифагора величайшим философом Греции, покупал труды пифагорейцев и часто цитировал их суждения в своих трудах.
Основные достижения
Пифагор считал, что в основе любой вещи лежит число, и изучить мир – значит изучить управляющие им числа. Он был великим математиком и создал одну из самых известных теорем: квадрат гипотенузы равен сумме квадратов катетов. Считается, что сам Пифагор не доказывал эту теорему, он лишь передал людям знание. И вполне успешно! На данный момент в современном научном мире существует уже более 300 доказательств теоремы Пифагора, которая приняла основополагающее значение для геометрии.
Ещё одним фундаментальным трудом греческого философа стала «таблица Пифагора», проще говоря, таблица умножения. Она актуальна для миллионов людей по всему миру и в наши дни. Помимо математики Пифагор большое количество времени уделял нумерологии, философии и астрономии. В некоторых источниках говорится, что он был одним из первых учёных, кто установил, что Земля круглая.
Он много говорил о космосе, о разных способах движения небесных сфер и светил, о затмениях, об отклонениях от правильного движения, об эксцентриситетах, эпициклах и дифферентах.
Своим ученикам он старался донести: «Прекрасно зрелище небосвода и движущихся по нему светил для тех, кто способен усмотреть порядок в этом движении, причастность к первосущему и умопостигаемому — числам и пропорциям».
Пифагор учил, что Солнце и другие звезды — боги, и в них преобладает тепло — причина жизни.
Пифагор также говорил, что движутся не только планеты, но и неподвижные звезды, однако они движутся и совершают собственное круговращение таким же образом, как Вселенная, т. е. не поступательно, а крутясь на месте подобно бураву.
Пифагору приписывают книги, связанные с природой, государством и воспитанием, однако большинство его работ не удалось сохранить. Великий философ практически ничего не записывал, он предпочитал передавать свои учения устно, да и допускал к ним далеко не всех, только избранных и «просвещённых» личностей. Кстати, именно на одной из лекций Пифагор познакомился со своей будущей супругой, которую звали Феано. Предполагается, что ему тогда было уже за 50 лет, а то и за 60 лет. У пары в браке появились двое детей, сын и дочь, точные их имена неизвестны.
Таблица Пифагора
Интересные факты
- Интересно, что рождение Пифагора предсказала дельфийская Пифия (отсюда и такое имя, ведь «Пифагор» в переводе с греческого – «предсказанный Пифией»). Отец мальчика был предупреждён о том, что его сын родится необычайно одарённым и принесёт много пользы людям.
- Многие биографы по-разному описывают жизнь Пифагора. Определённые разночтения есть в трудах Гераклида, Ефсевия Кесарийского, Диогена, Порфирия. Согласно трудам последнего, философ либо погиб в результате антипифагорейского мятежа, либо сам уморил себя голодом в одном из храмов, так как не был удовлетворён результатами своего труда.
- Существует мнение о том, что Пифагор был вегетарианцем и только изредка позволял себе есть рыбу. Аскетизм во всём – одно из составляющих учения пифагорейской философской школы.
Главные этапы образования
Первым учителем будущего философа стал Гермодамант. Он научил Пифагора основам музыки, технологиям живописного искусства, чтению, риторике, грамматике. Чтобы помочь Пифагору развить память, учитель заставлял читать «Одиссею» и «Илиаду» Гомера и заучивать наизусть песни из поэм.
По совету наставника Пифагор отправляется учиться у египетских жрецов. Но перед этим знакомится с философом Ферекидом, его учениями по астрологии, медицине, тайнам чисел. Большое влияние на будущего гениального ученого оказали и лекции философа Фалеса, которые он прослушал в Милете.
Усовершенствуя свои знания в Египте, у мемфисских старцев, Пифагор становится одним из самых образованных людей не только Древней Греции, но и других стран. Даже свое пленение персами он использовал для того, чтобы повстречаться с персидскими магами, получить новые знания о восточной астрологии, мистике. Учения магов сказались в дальнейшем на характере работ Пифагора, ведь даже его математические трактаты имеют мистическое звучание.
Десятка может быть выражена суммой первых четырех чисел (1+2+3+4=10), где единица — выражение точки, двойка — линии и одномерного образа, тройка — плоскости и двумерного образа, четверка — пирамиды, то есть трехмерного образа. Ну чем не четырехмерная Вселенная Эйнштейна?
Бюст Пифагора
Освобождение и возвращение на родину
По прошествии 12 лет в неволе Пифагора отпускает на свободу сам царь Персии, до которого уже дошли слухи о выдающемся ученом. Пифагор отправляется домой и по прибытию начинает делиться знаниями со своими соотечественниками.
Ученый быстро нашел общий язык с ними и обрел среди них большую популярность. В то время женщинам не разрешалось присутствовать на обоих собраниях. Но даже они приходили послушать лекции Пифагора. Именно на одном из таких собраний он встретил свою будущую супругу.
Образованному ученому пришлось обучать людей, которые не могли похвастаться высоким уровнем образования. Многие из них не выделялись еще и высоким уровнем нравственности. Но Пифагору удалось стать примером для них и прослыть человеком образованным и воспитанным.
Со своими лекциями и нравоучениями ему приходилось выступать прямо на городских улицах, а в последствии образовательный процесс проходил в его доме. Проходить обучение под руководством Пифагора было трудной задачей. Ученикам предлагалось первоначально пройти испытательный срок, который длился от 3 до 5 лет. На занятиях запрещалось вести разговоры, задавать вопросы преподавателю, что воспитывало в них терпение и прилежание.
Математика
В биографии Пифагора важное место занимает математика. Молодой ученый делился своими знаниями в области арифметики и геометрии, философии, медицины, музыки и др. Многие его ученики стали известными государственными служащими, учеными и исследователями.
Сложно оценить вклад ученого, который он внес в развитие геометрии. Биография Пифагора как математика обязана включать в себя упоминание о его самом знаменитом достижении.
Современным школьниками имя ученого известно благодаря его теореме для прямоугольного треугольника. Вместе с основной теоремой существует еще и обратная ей, которая была разработана другими учеными-математиками. На сегодняшней день существует около 400 доказательств знаменитой теоремы, что свидетельствует о ее фундаментальном значении для такой науки как математика.
Еще одним примечательным достижением Пифагора стала его таблица умножения, которая была названа его именем. Именно по ней обучались школы, которая была им основана.
В сферы интересов Пифагора попадали и сами числа, природу которых ученый пытался познать. Знаменитый ученый связал численные свойства с такими жизненными категориями как смерть, болезни, человечество и т. п. Последователи школы Пифагора первыми предложили разделить все числа на две группы: четные и нечетные. Отсюда берет свое начало такая наука как нумерология.
С помощью нумерологии можно узнать, насколько совместимы два человека, благодаря так называемому «квадрату Пифагора». Своеобразная «игра» с числом даты рождения позволяет приоткрыть завесу тайны будущего человека и его второй половины.
Информационные источники
Доклад или сообщение о Пифагоре разумно начинать с биографии мыслителя. Однако в этом и заключается основная трудность, поскольку в настоящее время неизвестен ни один полный письменный источник, который можно отнести к жизни этого великого философа. Не существует ни одной автобиографии, более того, ни один непосредственный ученик Пифагора не написал о нем ни строчки.
Первые письменные свидетельства о жизни этого древнего грека появились спустя 150−250 лет после его смерти. Основаны они на легендах, рассказах и анекдотах, которые ходили в устной речи того времени, что говорит об их сомнительной достоверности. Отсутствие биографии Пифагора, которая была бы написана его современниками, связано с основными принципами, которые философ пропагандировал при жизни:
- герметизм и аскетизм среди своих учеников;
- существование эзотерических обычаев и мистических символов;
- запрет на распространение получаемых знаний среди простого люда.
Наиболее обширная и содержащая множество деталей из жизни Пифагора работа датируется III веков нашей эры, то есть спустя 800 лет после смерти философа! Принадлежит она двум грекам Диогену Лаэртскому и Порфирию и называется «Жизни Пифагора».
Также существует еще одна работа философа Ямблиха, которая называется «О жизни Пифагоровой». Можно смело сказать, что за несколькими исключениями эти произведения являются единственными о Пифагоре, которыми располагает современный мир. При этом Диоген, в отличие от Порфирия и Ямблиха, придерживался некоторой исторической строгости в своем труде.
Обе работы относятся к такому периоду в жизни Античной Греции, когда пифагоровой фигуре приписывались почти сверхъестественные способности. Полагалось, что этот философ единственный, кто владел «правдивыми знаниями», которые впоследствии были присвоены Аристотелю и Платону. Как бы там ни было, оба ученых в своих работах действительно признают величие Пифагора и его огромный вклад в развитие многих отраслей науки.
Пифагор интересные факты. Легенды и мифы о Пифагоре: удивительная жизнь
Пифагор — одна из самых известных личностей Древней Греции — практически всю жизнь провел за пределами родины. 22 года он учился в Египте, еще 12 жил с вавилонскими магами, а после 50 обосновался в нынешней Калабрии (Италии), где и основал религиозное общество с «Советом трехсот». Именно за этот мир «идеальных убеждений» его обожали и ненавидели.
А теорема, названная в честь великого ученого и философа, благодаря которой его сегодня знает каждый школьник, выглядела на фоне тех деяний лишь малым дополнением.
Впрочем, в пифагорово авторство ее доказательства верят лишь единицы историков. Большинство экспертов сходятся во мнении, что это знание он почерпнул то ли у финикийцев, то ли у вавилонских магов. Те же историки утверждают, что доподлинно о жизни гения известно очень мало.
История сохранила больше легенд о нем, чем фактов. Зато мифы и легенды невероятно разнообразны и порой противоречивы. Вот несколько особенно ярких примеров.
- По преданию, у Пифагора было золотое бедро. Сомневающимся в его божественном происхождении достаточно было увидеть его блеск, чтобы отказаться от всех возражений.
- Один из вавилонских магов подарил ему волшебную золотую палочку. С ее помощью сын Гермеса (так называл себя Пифагор) летал по воздуху и управлял самой природой.
- Чтобы получить от богов доказательство теоремы Пифагора, он принес в жертву несколько быков (или волов, здесь «показания» учеников расходятся).
Правила Пифагора
Пифагор был не только выдающимся ученым и занимался просветительской работой. Одно из призваний гения — воспитание. Как вспоминали его ученики, мастер слова и первый философ истории для всего придумывал правила. Среди них были и такие:
- первым надевать правый ботинок;
- еду, упавшую на пол, уже не есть;
- употреблять в пищу ягнят — загрязнять чистую божественную душу. При этом курицу, свинину и мясо коз последователи и ученики могли вкушать сколько угодно, равно как и сам Пифагор. Потому что эти животные считались пифагорейцами неодушевленными.
Воздержание и обет молчания
Интересное правило касалось интимной жизни человека. Так, Пифагор рекомендовал своим поклонникам воздерживаться от связей с женщинами (и мужчинами — среди учеников были представительницы прекрасного пола) летом и «отводить душу» зимой.
Пифагор считал, что женщинам следует преподавать философию также как мужчинам. Многие видные члены его школы были женщинами. Иллюстрация 1913 года
Если верить воспоминаниям учеников, для новых последователей действовало правило молчания. Первые пять лет неофиты пифагорейской школы должны были сохранять обет. Нарушители изгонялись навсегда.
Фёдор Бронников «Гимн пифагорейцев солнцу»
Если многие легенды о Пифагоре выглядят неправдоподобными, то последнее вполне объяснимо. Первый философ сам называл себя сыном бога и фактически организовал государство в государстве с единовластным правителем. Подобная деятельность была предосудительной и могла привести к преследованиям гораздо раньше, чем это в итоге случилось. Потому молчание новичков было кстати.
За ширмой
К этому можно добавить еще несколько мифов о Пифагоре. Например, о том, как он разделил прихожан на математиков и последователей. Первыми могли стать лишь те, кто полностью посвятил себя «ордену», — продал имущество, отказался от мяса и женщин. С ними учитель встречался лично и обсуждал свои открытия. Последователям же тайна лица Мастера не открывалась — они видели лишь профиль Пифагора за натянутой тканью.
Пифагор, появившийся из подземного мира — Сальватор Роза (1662 г.)
Убийство Гиппаса
Гиппас — один из самых известных учеников гения — был математиком и постоянно работал с учителем над разгадкой тайн арифметики. По легенде, это его и погубило. Миф рассказывает, что Гиппас открыл иррациональное число, и это полностью противоречило учениям Пифагора. За что последний в буквальном смысле утопил своего верного слушателя в реке.
Гиппас из Метапонта
Правда, как раз последний факт многими историками считается выдумкой. Есть мнение, что «страшилку» придумали сами пифагорейцы для устрашения новичков и чужаков, которые могли выдать тайны сообщества в Кротоне («Совет трехсот»).
Пифагор и животные
Историки считают, что Пифагор не только не пресекал распространение мифов и небылиц о себе, но и поощрял их. Так родилась легенда о том, как он отговорил быка есть зеленые бобы, пошептавшись с ним полчаса.
Пифагор поворачивает лицо от бобов (Французская рукопись 1512/1514)
Или одним словом отправил вола в огонь (животное добровольно отправилось в языки пламени), чтобы принести жертву богам ради знаний.
Была и история о том, как Пифагор накинулся на группу горожан, которые гнали палками бездомного пса. Ученый узнал в скулеже животного голос своего друга (в одной из реинкарнаций) и велел людям прекратить избиения.
- Интересно? Ставьте лайк и подписывайтесь на канал ΦΙΛΟΣΟΦΊΑ. Ещё нас можно читать во ВКонтакте!
Историю жизни Пифагора трудно отделить от легенд, представляющих его в качестве совершенного мудреца и великого посвящённого во все таинства греков и варваров. Ещё Геродот называл его «величайшим эллинским мудрецом». Основными источниками по жизни и учению Пифагора являются сочинения философа-неоплатоника Ямвлиха, «О Пифагоровой жизни»; Порфирия «Жизнь Пифагора»; Диогена Лаэртского, «Пифагор». Эти авторы опирались на сочинения более ранних авторов, из которых следует отметить ученика Аристотеля Аристоксена родом из Тарента, где сильны были позиции пифагорейцев.
Краткая биография Пифагора:
Самые ранние из известных источников об учении этого мыслителя появились только спустя 200 лет после его смерти. Однако именно на них основывается биография Пифагора. Сам он не оставил потомкам сочинений, поэтому все сведения о его учении и личности основываются лишь на трудах последователей, которые не всегда были беспристрастны.
Родился Пифагор в Сидоне Финикийском около 580 (по другим источникам около 570 ) года до н. э. Родители Пифагора — Партенида и Мнесарх с острова Самос. Отец Пифагора был, по одной версии, камнерезом, по другой — богатым купцом, получившим гражданство Самоса за раздачу хлеба во время голода. Предпочтительнее представляется первая версия, так как Павсаний, который свидетельствовал об этом, приводит генеалогию этого мыслителя. Партенида, мать его, позднее была мужем переименована в Пифаиду. Она происходила из рода Анкея, знатного человека, основавшего на Самосе греческую колонию.
Великая биография Пифагора была якобы предопределена еще до его рождения, которое как будто было предсказано в Дельфах Пифией, поэтому его назвали именно так. Пифагор означает «тот, о ком было объявлено Пифией». Эта предсказательница сообщила будто бы Мнесарху, что будущий великий человек принесет столько добра и пользы людям, сколько никто другой впоследствии. На радостях от этого отец ребенка даже дал новое имя своей жене, Пифаида, а сына своего назвал Пифагором «тем, о ком было объявлено Пифией».
Существует другая версия появления этого имени. Более того, говорят, что это прозвище, и получено оно им за способность изрекать истину. От имени жрицы-прорицательницы из храма Аполлона Пифии. И значение его – «убеждающий речью».
Известно имя первого его учителя. Им был Гермодамас. Этот человек, который привил ученику любовь к живописи и музыке, познакомил с «Иллиадой» и «Одиссеей».
Восемнадцатилетним юношей покинул Пифагор родной остров. Спустя несколько лет, проведенных в путешествиях и во встречах с мудрецами из разных краев, прибыл в Египет. В его планы входит обучение у жрецов, постижение древних премудростей. В этом ему помогает рекомендательное письмо тирана Самосса Поликрата к фараону Амасису. Теперь ему доступно то, о чем не могут даже мечтать многие чужеземцы: не только математика и медицина, но и таинства. Пифагор провел здесь целых 22 года. И покинул страну в качестве пленника царя Персии Камбиза, завоевавшего Египет в 525 году до н.э. Следующие 12 лет прошли в Вавилоне.
На родной Самос он смог вернуться лишь в 56, и был признан соотечественниками мудрейшим из людей. У него здесь нашлись и последователи. Многих привлекает мистическая философия, здоровый аскетизм и строгая мораль. Проповедовал Пифагор нравственное облагораживание народа. Его можно было достичь там, где власть находится в руках знающих и мудрых людей, которым повинуется народ безоговорочно в одном и сознательно в другом, как нравственному авторитету. Именно Пифагору приписывает традиция введение таких слов, как «философ» и «философия».
Ученики этого мыслителя образовали религиозный орден, своеобразное братство посвященных, которое состояло из касты единомышленников, обожествлявших учителя. Данный орден в Кротоне фактически пришел к власти. Все члены ордена становились вегетарианцами, которым ни есть мясо, ни жетвенных зверей приносить богам запрещено было. Употреблять пищу животного происхождения – то же самое, что и заниматься каннибализмом. История сохранила даже забавные порядки в этом почти религиозном ордене. Например, они не позволяли ласточкам вить гнезда под крышами своих домов, или не могли дотрагиваться до белого петуха, или бобы есть. Существует и иная версия, по которой ограничение действовало лишь в отношении определенных видов мяса.
По свидетельству авторов биографии, у Пифагора была жена, которую звали Феано, а также дочь Мия и сын Телавг (по другой версии, имена детей были Аригнота и Аримнест).
В конце 6 века до н. э. из-за антипифагорейских настроений философу пришлось отправиться в Метапонт, другую греческую колонию, где он скончался. Здесь через 450 лет, во время правления Цицерона (I век до н. э.), показывали склеп этого мыслителя в качестве местной достопримечательности. Как и дата его рождения, точная дата смерти Пифагора неизвестна, только предполагается, что он прожил 80 лет.
Пифагор, по Ямвлиху, возглавлял тайное общество 39 лет. Основываясь на этом, дата смерти его — 491 год до н. э., когда начался период греко-персидских войн. Ссылаясь на Гераклида, Диоген говорил, что этот философ умер в возрасте 80 лет, или даже в 90, по другим неназванным источникам. То есть дата смерти отсюда — 490 год до н. э. (или, что маловероятно, 480). В своей хронологии Евсевий Кесарийский указал как год смерти этого мыслителя 497 до н. э. Таким образом, биография этого мыслителя во многом вызывает сомнения.
Научные достижения и труды Пифагора:
Самые ранние известные источники об учении Пифагора появились лишь 200 лет спустя после его смерти. Сам Пифагор не оставил сочинений, и все сведения о нём и его учении основываются на трудах его последователей, не всегда беспристрастных.
1) В области математики:
Пифагор сегодня считается великим космологом и математиком древности, но ранние свидетельства не упоминают о подобных заслугах. Ямвлих пишет про пифагорейцев, что у них существовал обычай приписывать своему учителю все достижения. Этот мыслитель считается античными авторами создателем известной теоремы о том, что в прямоугольном треугольнике квадрат гипотенузы равняется сумме квадратов его катетов (теорема Пифагора). Как биография этого философа, так и его достижения, является во многом сомнительной. Мнение о теореме, в частности, основано на показаниях Аполлодора-исчислителя, личность которого не была установлена, а также на стихотворных строках, авторство которых также остается загадкой. Историки современности предполагают, что этот мыслитель теорему не доказывал, но мог передать это знание грекам, которое было известно еще за 1000 лет в Вавилоне до того времени, каким датируется биография математика Пифагора. Хотя существует сомнение в том, что сделать это открытие удалось именно этому мыслителю, нельзя найти весомых аргументов для того, чтобы оспорить данную точку зрения. Кроме доказательства вышеупомянутой теоремы, этому математику также приписывают изучение целых чисел, их свойств и пропорций.
2) Открытия Аристотеля в области космологии:
Аристотель в работе «Метафизика» затрагивает развитие космологии, но вклад Пифагора никак не озвучен в ней. Интересующему нас мыслителю приписывают также открытие того, что Земля круглая. Однако Феофраст, самый авторитетный в этом вопросе автор, отдает его Пармениду. Несмотря на спорные моменты, заслуги в космологии и математике школы пифагорейцев являются бесспорными. По Аристотелю, настоящими из них были акусматики, которые следовали учению о переселении душ. Они рассматривали математику как науку, исходящую не столько от их учителя, сколько от одного из пифагорейцев, Гиппаса.
3) Сочинения, созданные Пифагором:
Не писал никаких трактатов этот мыслитель. Невозможно было составить труд из устных наставлений, обращенных к простому народу. А тайное оккультное учение, предназначенное для избранных, доверить книге было также нельзя. Диоген перечисляет некоторые названия книг, будто бы принадлежавших Пифагору: «О природе», «О государстве», «О воспитании». Но за первые 200 лет, прошедшие после его смерти, ни один из авторов, включая Аристотеля, Платона, а также их преемников в Лицее и Академии, не приводит никаких цитат из сочинений Пифагора и даже не указывает на их существование. Античным писателям с начала новой эры были неизвестны письменные работы Пифагора. Об этом сообщают Иосиф Флавий, Плутарх, Гален. Компиляция из высказываний этого мыслителя появилась в III веке до н. э. Она называется «Священное слово». Позднее из нее возникли «Золотые стихи» (которые относят иногда, без веских причин, к IV веку до н. э., когда рассматривается различными авторами биография Пифагора).
4) Кружка Пифагора:
Довольно хитрое изобретение. Не представляется возможным налить ее до краев, потому что все содержимое кружки сразу вытечет. Жидкость должна быть в ней только до определенного уровня. С виду обычная кружка, отличает ее от других колонка в центре. Она получила название «кружки жадности». Даже сегодня в Греции она пользуется заслуженным спросом. А не знающим меры в потреблении спиртного, она даже рекомендуется.
5) Ораторский талант:
Его у Пифагора никто не подвергает сомнению. Оратором он был великим. Доподлинно известно, что после самой первой его публичной лекции у него появились ученики, две тысячи. Целыми семьями они, проникнувшись идеями своего учителя, готовы были начать новую жизнь. Их пифагорейское сообщество стало своеобразным государством в государстве. Все правила и законы, выработанные Учителем, действовали в их Великой Греции. Собственность здесь была коллективной, даже научные открытия, которые, кстати, приписывались исключительно Пифагору, относились к его личным заслугам даже, когда учителя уже не было в живых.
Пифагор — цитаты, афоризмы, высказывания:
*Две вещи делают человека богоподобным: жизнь для блага общества и правдивость.
*Как старое вино непригодно к тому, чтобы его много пить, так и грубое обращение непригодно для собеседования.
*Берегите слезы ваших детей, дабы они могли проливать их на вашей могиле.
*Одинаково опасно и безумному вручать меч и бесчестному власть.
*Не считай себя великим человеком по величине твоей тени при заходе солнца.
*Из двух человек одинаковой силы сильнее тот, кто прав.
*Как ни коротки слова «да» и «нет», все же они требуют самого серьезного размышления.
*Для познания нравов какого ни есть народа старайся прежде изучить его язык.
*Полезнее наобум бросить камень, чем пустое слово.
*Живи с людьми так, чтобы твои друзья не стали недругами, а недруги стали друзьями.
*Никто не должен преступать меру ни в пище, ни в питии.
*Будь благословенно божественное число, породившее богов и людей.
*Шутку, как и соль, нужно употреблять с умеренностью.
*Для того чтобы жить долго, приобрети для себя старого вина и старого друга.
*Законодательство должно быть голосом разума, а судья — голосом закона.
*Избери лучшее, а привычка сделает его приятным и легким.
*Во время гнева не должно ни говорить, ни действовать.
*Статую красит вид, а человека — его деяния.
*Лесть подобна оружию, нарисованному на картине. Она доставляет приятность, а пользы никакой.
*Не гоняйся за счастьем: оно всегда находится в тебе самом.
30 интересных фактов о Пифагоре:
1.Имя Пифагора знаменито по его теореме. И это является самым большим достижением этого человека.
2.Давно известно имя «отца» демократии. Это Платон. Но в основу своего учения им положены идеи Пифагора, можно сказать, дедушки.
3.По мнению Пифагора, все в мире отражается в цифрах. Любимым его числом было 10.
4.Ни в одном из свидетельств раннего времени нет упоминаний о заслугах Пифагора как величайшего космолога, математика древности. А таковым он считается сегодня.
5.Уже при жизни он считался полубогом, чудотворцем и абсолютным мудрецом, своего рода Эйнштейном IV века до нашей эры. Нет более загадочного великого человека в истории.
6.Однажды Пифагор рассердился на одного из своих учеников, который покончил с собой от горя. Философ с тех пор решил не выплескивать больше никогда свое раздражение на людей.
7.Приписывали Пифагору предания также умение исцелять людей, используя, в том числе, прекрасное знание различных лекарственных растений. Влияние на окружающих этой личности трудно переоценить.
8.В действительности Пифагор это не имя, а прозвище великого философа.
9.Пифагор отличался прекрасной памятью и развитой любознательностью.
10.Пифагор был знаменитым космологом.
11. Всегда было окружено имя Пифагора множеством легенд еще при его жизни. Например, считалось, что он был способен управлять духами, знал язык животных, умел прорицать, а птицы могли изменить направление полета под влиянием его речей.
12.Пифагор первым сказал, что душа человека после его смерти снова возрождается.
13.С юных лет Пифагора тянуло к путешествиям.
14.У Пифагора была собственная школа, которая включала в себе 3 направления: политическое, религиозное и философское.
15.Пифагор проводил эксперименты с цветом на психику людей.
16.Пифагор старался найти гармонию чисел в природе.
17. Пифагор считал себя в прошлой жизни борцом за Трою.
18.Теория музыки была развита именно этим талантливым мудрецом.
19.Пифагор погиб, спасая от пожара собственных учеников.
20. Рычаг был придуман этим философом.
21.Великим оратором был Пифагор. Он этому искусству обучал тысячи людей.
22.В честь Пифагора назван кратер на Луне.
23.Пифагор всегда считался мистиком.
24.Пифагор считал, что секрет всей сущности на Земле заключается в числах.
25.Женился Пифагор, когда ему было 60 лет. И женой стала ученица этого философа.
26.Первая лекция, которую прочел Пифагор, привела к нему 2000 человек.
27.Вступая в школу Пифагора, людям приходилось отказываться от своего имущества.
28.Среди последователей этого мудреца были достаточно знатные люди.
29.Первые упоминания о жизни и деятельности Пифагора стали известны лишь после того, как прошло 200 лет со дня его смерти.
30.Школа Пифагора попала под немилость государства.
фото из интернета
Начало жизненного пути
Биография Пифагора начинается в 570 году (дата приблизительная), в городе Сидоне (ныне Сайда, Ливан). Он родился в семье зажиточного ювелира, который смог дать самое лучшее воспитание и знания своему сыну. Интересным фактом является происхождение имени будущего мудреца. Его отец, Мнесарх, назвал сына в честь одной из жриц Аполлона, Пифии. Также в честь нее он назвал и свою жену – Пифазис. А все так сложилось потому, что именно эта жрица предсказала Мнесарху, что у него родится сын, который превзойдет каждого другого человека и по красоте, и по своему уму.
Философия и мистика
Хотя точные детали учений и философии Пифагора не вполне ясны, всё-таки можно кратко восстановить общую схему и содержание его идей. Подробно об учении пифагорейцев пишет древнегреческий философ Аристотель, но непосредственного упоминания основателя школы нет. Одной из главных доктрин мыслителя, по-видимому, был метемпсихоз — вера в то, что все души бессмертны и просто переселяются в новые тела, когда предыдущее умирает. Между прочим, на это учение ссылается даже Геродот. Однако ничего не известно о природе или механизме, с помощью которого происходит метемпсихоз.
Другое приписываемое Пифагору утверждение — гармония сфер. Якобы планеты и звёзды движутся в соответствии с математическими уравнениями, которые соответствуют музыкальным нотам, и таким образом создают неслышную симфонию. Говорили, философ практиковал гадание и прорицание.
Согласно записям Аристотеля, пифагорейцы использовали математику исключительно в мистических целях, лишённых практического применения. Они верили, что всё сделано из цифр, например:
- Один (монада) — представлял происхождение всех вещей.
- Два (диада) — материя.
- Три — идеальное число, поскольку имеет начало, середину и конец.
- Четыре — число сезонов и элементов.
- Семь — священное число. Столько планет и струн на лире, в конце концов, это день рождения Аполлона.
По мнению пифагорейцев, нечётные числа были мужскими, а чётные — женскими. Пятёрка представляла брак, поскольку это сумма двух и трёх. Пифагору приписывают разработку тетрактисов — треугольной фигуры, состоящей из четырёх рядов, которые в сумме составляют идеальное число — 10. Последователи мыслителя считали этот символ священным. В целом нумерология и квадрат Пифагора и сейчас используются в эзотерических целях.
Современные учёные спорят, является ли первоначалом этих учений разработки самого философа. В своём исследовании Уолтер Беркерт утверждает, что Пифагор был харизматичным политическим и религиозным учителем, но он вообще никогда не имел дела с цифрами, уже не говоря о том, чтобы внести какой-либо заметный вклад в математику. Пифагорейцы занимались простой арифметикой. Именно это имело значение в науке.
Смерть Пифагора
Школа, которую основал Пифагор, находилась в городе Кротон. Именно здесь произошло крупное восстание демократов и ученому пришлось уехать из него. Его путь лежал в Метапонт, но и здесь политическая обстановка была неспокойной.
У Пифагора было множество недоброжелателей, которые не разделяли его мировоззренческие взгляды. Точные обстоятельства смерти философа неизвестны. Существует три версии этого события, но большинство историков придерживаются мнения, что знаменитый математик трагически погиб во время одного из военных столкновений в Метапонте. На момент смерти ему было около 85 лет.
Открытия Аристотеля в области космологии
Аристотель в работе «Метафизика» затрагивает развитие космологии, но вклад Пифагора никак не озвучен в ней. Интересующему нас мыслителю приписывают также открытие того, что Земля круглая. Однако Феофраст, самый авторитетный в этом вопросе автор, отдает его Пармениду.
Несмотря на спорные моменты, заслуги в космологии и математике школы пифагорейцев являются бесспорными. По Аристотелю, настоящими из них были акусматики, которые следовали учению о переселении душ. Они рассматривали математику как науку, исходящую не столько от их учителя, сколько от одного из пифагорейцев, Гиппаса.
Первые знания и учителя
Ранние годы ученого, как повествует биография Пифагора, проходили в стенах лучших храмов Греции. Еще в подростковом возрасте он пытался узнать как можно больше, читая работы других мудрецов, а также беседуя с духовными учителями. Среди них стоит выделить Ферекида Сиросского – величайшего древнегреческого космолога. Он помогает молодому Пифагору изучить математику, физику, астрономию. Также на долю Пифагора выпало общение с Гермодамантом, который научил его любить поэзию и все, что связано с искусством.
1
В Древней Греции Настоящей наукой математика стала только у древних греков. Это был удивительно талантливый народ, у которого есть чему поучиться даже сейчас, тысячи лет спустя. В древние времена Греция состояла из маленьких государств. Каждый раз, когда приходилось решать какой-нибудь важный государственный вопрос, горожане собирались на площадь, обсуждали его, спорили о том, как лучше сделать, а потом голосовали. Греки считали, что спор помогает найти самое лучшее, самое правильное решение – «В споре рождается истина». И в науке греки стали поступать также, как в народном собрании. Они не просто заучивали правила, а доискивались причины: почему правильно делать так, а не иначе. Каждое правило греческие математики старались объяснить, доказать, что оно действительно верное. Для этого они спорили друг с другом, рассуждали, старались найти в рассуждениях ошибки. Из правил складывались законы, из законов – наука математика.
2
Александрийская эпоха. Евклид. В самом конце I V века до н.э. важнейшие математические достижения учёных Древней Греции были систематизированы и изложены в «Началах» Евклида, с которого начинается новый, самый блестящий период развития древнегреческой математики, так называемая александрийская эпоха. Известно, что после смерти Александра Македонского его огромная империя распалась. При её разделе один из греко-македонских полководцев, Птолемей, сын Лага, стал править Египтом с новопостроенным городом Александрией. Птолемей основал знаменитый музей (храм муз, покровительниц науки и искусств), ставший высшим культурным и научным учреждением, центром научной мысли эпохи эллинизма. В состав музея входила и богатейшая Александрийская библиотека, насчитывавшая около томов (свитков). В Александрии в III – II вв. до н.э. сосредоточились знаменитые математики того времени: Евклид, Эратосфен, Аполлоний. К Александрийской математической школе относится также Архимед, хотя он жил в Сиракузах. В этот период геометрия отделяется от философии и достигает высокого уровня совершенства. К первым представителям Александрийской школы принадлежит Евклид.
3
Евклид Наречён: Евклид (в некоторых транскрипциях – Эвклид) Точная дата рождения неизвестна, известно лишь то, что он младше Птолемея 1 Сотера (306 – 283 г.до нашей эры), но старше Архимеда (287 – 212 г. до нашей эры). Обстоятельства рождения: по данным арабских хроник: «Евклид, сын Нуакрата, известный под именем «Геометра», по своему происхождению грек, по местожительству сириец, родом из небольшого городка Тира, недалеко от Афин. По другим данным, родина Евклида – Афины.
4
Евклид Александрийский Характер: В одном из своих сочинений математик Папп, живший в Александрии в 3-4 в.в. н.э., изображает Евклида, как человека исключительно честного, тихого и скромного, которому были чужды гордость и эгоизм. Семейное положение: неизвестно, но учитывая огромное научное наследие и безграничную любовь к геометрии, наверняка был холост. За что ценим: будучи основателем математической школы в Александрии, написал для её учеников фундаментальный труд, на тысячелетия определивший путь развития геометрии.
5
Евклид — учитель В свободное от математики время: одарённый от природы Евклид проявил себя и в совершенно неожиданных областях науки и культуры. В музыке – он изобретатель прообраза камертона – монохорда. В оптике – основатель геометрической оптики. Евклид преподавал в Александрии, куда был приглашён царём Птолемеем 1 Сотером для организации математической школы. Известно, что он учился в платоновской Академии в Афинах. Евклид был последователем древнегреческого философа Платона, и преподавал он вероятно, четыре науки, которые по мнению Платона должны предшествовать занятиям философией: арифметику, геометрию, теорию гармонии и астрономию.
6
Нет царской дороги к геометрии. Славу Евклиду принёс написанный около 325 года до н.э. для своих учеников Александрийской математической школы фундаментальный труд «Начала», в котором он подвёл итог построению геометрии, объединил результаты своих предшественников, упорядочил и привёл в одну систему основные геометрические знания того времени и придал изложению столь совершенную форму, что на 2000 лет «Начала» стали энциклопедией геометрии. Прокл в комментариях к первой книге «Начал» приводит рассказ о том, что будто бы царь Птолемей спросил Евклида, нельзя ли найти более короткий и менее утомительный путь к изучению геометрии, чем его «Начала». Евклид ответил: «Нет царской дороги к геометрии!». Так в виде легенды дошло до нас это ставшее крылатым выражение. Предшественники Евклида – Фалес, Пифагор, Аристотель и другие много сделали для развития геометрии. Но всё это были отдельные фрагменты.
7
Начала. Евклид с величайшим искусством расположил материал по 13 книгам так, чтобы трудности не возникали преждевременно. Все эти книги построены по единой логической схеме.Позже греческие математики включили в «Начала» ещё две книги – 14-ю и 15-ю, написанные другими авторами. В «Началах» Евклид придерживается аристотелевских принципов построения науки. Величайший философ древности – Аристотель жил и творил в период, непосредствованно предшествующий «Началам» Евклида. В трудах Аристотеля разъясняется сущность научных определений, аксиом и доказательств. Согласно Аристотелю, одно определение (например, квадрата) не говорит ещё о существовании определяемого. Существование следует доказать. Доказательством же служит построение. Именно эта и другие установки Аристотеля нашли своё отражение в «Началах» Евклида. Как и Аристотель, Евклид обозначает величины буквами. Первые шесть книг «Начал» посвящены планиметрии, 7-10 – учению о числе, – стереометрии. Оригинальная рукопись, которая долгое время сохранялась в Александрийском музее, не дошла до нас. Древнейшая из сохранившихся копий принадлежит IX веку. На русском языке «Начала» были изданы 3 раза в 18 веке и четыре раза в 19 веке. Последний и самый совершенный перевод с греческого на русский язык был осуществлён в г.г.
8
1-13 книги «Начал» В первой книге формулируются исходные положения геометрии, а также содержатся основополагающие теоремы планиметрии, среди которых теорема о сумме углов треугольника и теорема Пифагора. Во второй книге излагаются основы геометрической алгебры. С помощью геометрических чертежей даются решения задач, сводящихся к квадратным уравнениям. Алгебраической символики тогда не существовало. Третья книга посвящена свойствам круга, его касательных и хорд. В четвёртой книге рассматриваются правильные многоугольники, причём построение правильного пятнадцатиугольника принадлежит, видимо, самому Евклиду. Появляются основы учения о подобии. Книги 5-я и 6-я посвящены теории отношений и её применению к решению алгебраических задач. Книги 7-я, 8- и 9-я посвящены теории целых и рациональных чисел, разработанной пифагорейцами не позднее 5в. до н.э. Приводится алгоритм нахождения наибольшего общего делителя. В книге 10-й рассматриваются квадратичные иррациональности и излагаются результаты, полученные Теэтетом. В книге 11-й рассматриваются основы стереометрии. В 12-й книге доказываются теоремы, относящиеся к площади круга и объёму шара, выводятся отношения объёмов пирамид, призм и конусов. В основу 13-й книги легли результаты, полученные Теэтетом в области правильных многогранников. В «Начала» не попало одно из величайших достижений греческих геометров – теория конических сечений. О них Евклид написал отдельную книгу «Начала конических сечений», не дошедшую до нас, но её цитировал в своих сочинениях Архимед.
9
Евклидова геометрия «Начала» Евклида представляют собой изложение той геометрии, которая ивестна и поныне под названием Евклидовой геометрии. Начиная с III в. до н.э. и до середины 19 века «Начала» считались образцом строго логического изложения геометрии. Евклид исходит из определений геометрических понятий и аксиом. Каждое геометрическое понятие формулируется в общих выражениях, затем конкретно указывается на чертеже то, что дано и что требуется доказать или построить. После доказательства следует заключение, повторяющее начальную формулировку и заканчивающееся словами: «что и требовалось доказать» или «что и требовалось сделать». На протяжении многих столетий до 19 века геометрия изучалась в школах по «Началам» Евклида. Наши современные учебники имеют много общих черт с «Началами»: планиметрия и стереометрия излагаются раздельно, каждая из них примерно в том же порядке, что и у Евклида; теоремам предшествуют определения и аксиомы. Многие теоремы, изложенные в современных учебниках, совпадают с теми, которые имеются в «Началах», методы доказательства в большинстве случаев те же. Но есть и различия. В «Началах» даже не упоминается о непосредственном измерении площадей и объёмов фигур, а только об их сравнении. Так, например, у Евклида нет теоремы о том, что площадь треугольника равна половине произведения его основания на высоту; имеется только теорема о том, что треугольник равновелик половине параллелограмма с тем же основанием и той же высотой. В «Началах» нигде не говорится о числе π и его приближённом значении. Все теоремы и их доказательства излагаются в чисто геометрической форме. Евклид не вычисляет длин, площадей, объёмов (таких слов даже нет в книге), а находит посредством геометрических построений соотношения между величинами геометрических фигур. В «Началах» все предложения расположены в виде цепи логических рассуждений и выводов, исходя из простых аксиом и доходя постепенно до сложных теорем.
10
1 книга Евклида. Определения и постулаты. 1 книга Евклида. Определения и постулаты. Первая книга Евклида начинается с 23 определений, среди них такие: Точка есть то, что не имеет частей. Линия есть длина без ширины. Границы линии суть точки. Прямая есть такая линия, которая одинаково расположена по отношению ко всем своим точкам. Поверхность есть то, что имеет длину и ширину. Границы поверхности суть линии. Плоскость есть поверхность, которая одинаково расположена по отношению ко всем прямым, на ней лежащим. Плоский угол есть взаимное наклонение двух встречающихся линий, расположенных в одной плоскости. Такие определения нельзя считать логически корректными. Во-первых, в этих определениях употребляются такие понятия, которые сами должны быть определены (часть, длина, ширина, граница). Во-вторых, идея основных понятий у Евклида вообще отсутствует. За определениями следуют 5 постулатов и 9 аксиом, которые Евклид не отождествлял Постулаты. 1.Требуется, чтобы от каждой точки ко всякой другой точке можно было провести прямую линию. 2.И чтобы каждую прямую можно было неопределённо продолжить. 3.И чтобы из любого центра можно было описать окружность любым радиусом. 4. И чтоб все прямые углы были равны. 5. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых. Это знаменитый постулат. Многочисленные попытки в 19 столетии «поправить» Евклида, сделать из этой аксиомы теорему закончились провалом.
11
Аксиомы 1. Равные порознь третьему равны между собой. 2.И если к равным прибавим равные, то получим равные. 3.И если от равных отнимем равные, то получим равные 4.И если к неравным прибавим равные, то получим неравные. 5.И если удвоим равные. То получим равные. 6.И половины равных равны между собой. 7.И совмещающиеся равны. 8.И целое больше части. 9.И две прямые не могут заключать пространства. Важнейшим недостатком системы евклидовых аксиом, включая и его постулаты, является их неполнота, то есть недостаточность их для строго логического построения геометрии. Лишь в 19 веке удалось выяснить, что Евклид перечислил далеко не все аксиомы, которые на самом деле нужны для построения геометрии. В действительности при доказательствах учёный ими пользовался, но не сформулировал. Но это нисколько не умаляет роли Евклида, первого показавшего, как можно и как нужно строить математическую теорию. А значит, все последующие математики в известной степени являются учениками Евклида.
12
Задачи по геометрии и их решения Из 1-й книги «Начал» 1. Данный прямолинейный угол рассечь пополам. 2.Данную ограниченную прямую(т.е. отрезок) рассечь пополам. Из 3-й книги «Начал» 1.Найти центр данного круга. 2.Рассечь данную дугу пополам. Из 4-й книги «Начал» 1.В данный круг вписать хорду данной длины. Из 6-й книги «Начал» 1.Для данных двух отрезков найти средний пропорциональный. 2.Для трёх данных отрезков найти четвёртый средний пропорциональный. 1.Чтобы разделить угол ВАС пополам, Евклид берёт на АВ произвольную точку D и на АС откладывает АЕ = А D. Далее, на DЕ он строит равносторонний треугольник DЕF. Прямая АF делит угол ВАС пополам. 2.Чтобы разделить отрезок АВ пополам, Евклид строит на нём равносторонний треугольник АВС, делит угол АСВ пополам прямой СD. Точка D – середина отрезка АВ. 3. Доказательство Евклида (методом от противного) сводится к тому, что центр круга лежит на перпендикуляре, восстановленном из середины хорды. 4.Евклид делит пополам хорду АВ, стягивающую данную дугу. Из точки С, середины хорды, он строит перпендикуляр к АВ, пересекающий дугу в искомой точке D.
13
Алгоритм Евклида Алгоритм Евклида – это способ нахождения наибольшего общего делителя двух целых чисел, двух многочленов, а также наибольшей общей меры двух соизмеримых отрезков. Чтобы найти наибольший общий делитель двух целых положительных чисел, нужно сначала большее число разделить на меньшее, затем второе число разделить на остаток от первого деления, потом первый остаток –на второй и т.д. Последний ненулевой остаток в этом процессе и будет наибольшим общим делителем данных чисел. Пример: Найти НОД 777 и = 629 * = 148 * = 37 * 4. Последниё ненулевой остаток 37 и есть наибольший общий делитель чисел 777 и 629. Для нахождения наибольшей общей меры двух отрезков поступают аналогично. Операцию деления с остатком заменяют его геометрическим аналогом: меньший отрезок откладывают на большем столько раз, сколько возможно: оставшуюся часть большего отрезка откладывают на меньшем отрезке и т.д. Последниё ненулевой остаток даст наибольшую меру этих отрезков.
14
Популярный памятник древности Обычно о «Началах» говорят, что после Библии это самый популярный написанный памятник древности. В течение 2000 лет эта книга являлась настольной книгой школьников, использовалась как начальный курс геометрии. «Начала» пользовались исключительной популярностью, с них было снято множество копий трудолюбивыми писцами в разных странах и городах. Позднее «Начала» с папируса перешли на пергамент, а затем на бумагу. До 20 века книга считалась основным учебником не только для школ, но и для университетов. «Начала» Евклида – образец дедуктивного (от общего к частному) изложения геометрии, алгебраические выводы сделаны в геометрическом стиле. Впоследствии геометрия развивалась, появилась неевклидова геометрия, геометрия стала экспериментальной наукой в физике. Но предпосылками этого развития стали именно труды великого Евклида.
15
Другие сочинения «Данные» — задачи, решаемые с помощью геометрической алгебры. «О делении фигур» — задачи на построение. «Явления» — астрономическое сочинение. «Оптика» «Сечения канона» — небольшой трактат, содержит десять задач о музыкальных интервалах. Изложение во всех этих сочинениях, как и в «Началах» подчинено строгой логике, причём теоремы выводятся из точно сформулированных физических гипотез и математических постулатов.
16
Выдающиеся геометры после Евклида Евклид умер между 275 и 270годами до н.э. Большой вклад в дальнейшее исследование различных вопросов геометрии внесли Архимед, Аполлоний Пергский. После Аполлония в Древней Греции не было крупных открытий в области геометрии.Труды Архимеда и Аполлония считались слишком сложными, они не читались, и часть их со временем была утеряна.