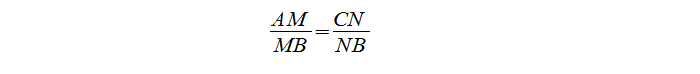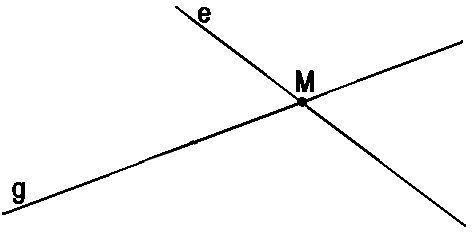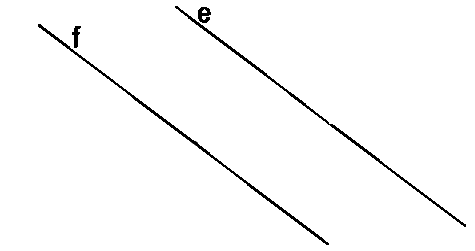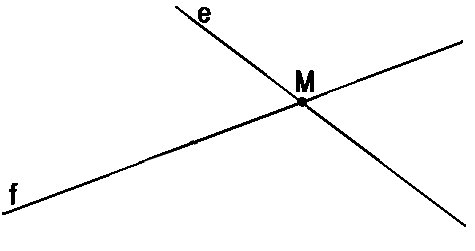Лежит как пишется в геометрии знак - Граматика и образование на Pisanino.ru

Символьные обозначения

Для обозначения геометрических фигур и их проекций, для отображения отношения между геометрическими фигурами, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем используются символьные обозначения.

Символьные обозначения, все их многообразие, может быть подразделено на две группы: – Первая группа – обозначения геометрических фигур и отношения между ними; – Вторая группа – обозначения логических операций, составляющая синтаксическую основу геометрического языка.

Символьные обозначения – Первая группа

Символы, обозначающие геометрические фигуры и отношения между ними

Обозначения геометрических фигур: Φ – геометрическая фигура; A, B, C, D, . L, M, N, . – точки расположенные в пространстве; 1, 2, 3, 4, . 12, 13, 14, . – точки расположенные в пространстве; a, b, c, d, . l, m, n, . – линии, произвольно расположенные по отношению к плоскостям проекций; h, υ(f), ω – линии уровня (горизонталь, фронталь, профильная прямая соответственно); (AB) – прямая проходящая через точки A и B; [AB) – луч с началом в точке A; [AB] – отрезок прямой, ограниченный точками A и B; α, β, γ, δ, . ζ, η, θ – поверхность; ∠ABC – угол с вершиной в точке B; ∠α, ∠β, ∠γ – угол α, угол β, угол γ соответственно; |AB| – расстояние от точки A до точки B (длина отрезка AB); |Aa| – расстояние от точки A до линии a; |Aα| – расстояние от точки A до поверхности α; |ab| – расстояние между прямыми a и b; |αβ| – расстояние между поверхностями α и β; H, V, W – координатные плоскости проекций (именуемые как горизонтальная, фронтальная, профильная соответственно); П₁, П₂, П₃ – координатные плоскости проекций (именуемые как горизонтальная, фронтальная, профильная соответственно); x, y, z – координатные оси проекций (ось абсцисс, ось ординат, ось аппликат); k_o – постоянная прямая эпюра Монжа; O – точка пересечения осей проекций; `, “, `” – верхние индексы для проекций точек, прямых, углов, фигур, поверхностей на плоскости проекций (именуемые как горизонтальную, фронтальную, профильную соответственно); 1, 2, 3 – верхние индексы для проекций точек, прямых, углов, фигур, поверхностей на плоскости проекций (именуемые как горизонтальную, фронтальную, профильную соответственно); α_H, α_V, α_W – след поверхности оставляемый на горизонтальной, на фронтальной, на профильной плоскости проекций соответственно; α_H, α_V, α_W – след поверхности α оставляемый на горизонтальной, на фронтальной, на профильной плоскости проекций соответственно; a_H, a_V, a_W – след прямой a оставляемый на горизонтальной, на фронтальной, на профильной плоскости проекций соответственно;

Проекции точек, линий, поверхностей любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса A`, A”, A`” или 1`, 1″, 1`”, соответствующего плоскости проекции, на которой они получены: A`, B`, C`, D`, . L`, M`, N`, . – горизонтальные проекции точек; A”, B”, C”, D”, . L”, M”, N”, . – фронтальные проекции точек; A`”, B`”, C`”, D`”, . L`”, M`”, N`”, . – профильные проекции точек; a`, b`, c`, d`, . l`, m`, n`, . – горизонтальные проекции линий; a”, b”, c”, d”, . l”, m”, n”, . – фронтальные проекции линий; a`”, b`”, c`”, d`”, . l`”, m`”, n`”, . – профильные проекции линий; α`, β`, γ`, δ`, . ζ`, η`, θ`, . – горизонтальные проекции поверхностей; α”, β”, γ”, δ”, . ζ”, η”, θ”, . – фронтальные проекции поверхностей; α`”, β`”, γ`”, δ`”, . ζ`”, η`”, θ`”, . – профильные проекции поверхностей;

Символы взаиморасположения геометрических объектов

Обозначение	Смысловое значение	Пример символической записи
(. )	способ задания геометрического объекта в пространстве и на комплексном чертеже	А(А`, А”) – точка А задана на комплексном чертеже горизонтальной и фронтальной проекциями; α(А, b) – плоскость α задана прямой b и точкой А.
∈ ⊂ , ⊃	принадлежность	А∈l – точка А принадлежит прямой l; l⊂α – прямая l лежит в плоскости α
≡	совпадение	А`≡ В` – горизонтальные проекции точек А и В совпадают.
‖ , //	параллельность	a // b – прямые a и b параллельны.
⊥	перпендикулярность	c⊥d – прямые c и d перпендикулярны.
∸	скрещивание	m ∸ n – прямые m и n скрещивающиеся.
∩	пересечение	k ∩ l – прямые k и l пересекаются.
∾	подобие	ΔАВС ΔDEF – треугольники ABC и DEF подобны.
≅	конгруэнтность	ΔАВС ≅ /АВ/ = /CD/ – отрезки АВ и CD равны.
=	равенство, результат действия	/АВ/ = /CD/ – длины отрезков AB и CD равны; k ∩ l = M – прямые k и l пересекаются в точке M.
/	отрицание	А ∉ l – точка А не принадлежит прямой l.
→ ←	отображение, преобразование	V/H → V1/H– система ортогональных плоскостей V/H преобразуется в систему плоскостей V1/H

Символьные обозначения – Вторая группа

Источник статьи: http://ngeo.fxyz.ru/%D1%81%D0%B8%D0%BC%D0%B2%D0%BE%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%BE%D0%B1%D0%BE%D0%B7%D0%BD%D0%B0%D1%87%D0%B5%D0%BD%D0%B8%D1%8F/

Обозначения и символика

Для обозначения геометрических фигур и их проекций, для отображения отношения между ними, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем в курсе используется геометрический язык, составленный из обозначений и символов, принятых в курсе математики (в частности, в новом курсе геометрии в средней школе).

Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:

группа I — обозначения геометрических фигур и отношений между ними;

группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.

Ниже приводится полный список математических символов, используемых в данном курсе. Особое внимание уделяется символам, которые применяются для обозначения проекций геометрических фигур.

СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ

А. Обозначение геометрических фигур

1. Геометрическая фигура обозначается — Ф.

2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:

3. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются строчными буквами латинского алфавита:

Линии уровня обозначаются: h — горизонталь; f— фронталь.

Для прямых используются также следующие обозначения:

(АВ) — прямая, проходящая через точки А а В;

[АВ) — луч с началом в точке А;

[АВ] — отрезок прямой, ограниченный точками А и В.

4. Поверхности обозначаются строчными буквами греческого алфавита:

Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:

α(а || b) — плоскость α определяется параллельными прямыми а и b;

β(d₁ d₂gα) — поверхность β определяется направляющими d₁ и d₂ , образующей g и плоскостью параллелизма α.

∠ABC — угол с вершиной в точке В, а также ∠α°, ∠β°, . , ∠φ°, .

6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:

— величина угла АВС;

— величина угла φ.

Прямой угол отмечается квадратом с точкой внутри

7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.

|АВ| — расстояние между точками А и В (длина отрезка АВ);

|Аа| — расстояние от точки А до линии a;

|Аα| — расстояшие от точки А до поверхности α;

|аb| — расстояние между линиями а и b;

|αβ| расстояние между поверхностями α и β.

8. Для плоскостей проекций приняты обозначения: π₁ и π₂, где π₁ – горизонтальная плоскость проекций;

π₂ —фрюнтальная плоскость проекций.

При замене плоскостей проекций или введении новых плоскостей последние обозначают π₃, π₄ и т. д.

9. Оси проекций обозначаются: х, у, z, где х – ось абсцисс; у – ось ординат; z – ось аппликат.

Постояшную прямую эпюра Монжа обозначают k.

10. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса, соответствующего плоскости проекции, на которой они получены:

А’, В’, С’, D’, . , L’, М’, N’, горизонтальные проекции точек; А”, В”, С”, D”, . , L”, М”, N”, . фронтальные проекции точек; a’ , b’ , c’ , d’ , . , l’, m’ , n’ , — горизонтальные проекции линий; а” ,b” , с” , d” , . , l” , m” , n” , . фронтальные проекции линий; α’, β’, γ’, δ’. ζ’,η’,ν’. горизонтальные проекции поверхностей; α”, β”, γ”, δ”. ζ”,η”,ν”. фронтальные проекции поверхностей.

11. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь или фронталь, с добавлением подстрочного индекса _0α, подчеркивающего, что эти линии лежат в плоскости проекции и принадлежат плоскости (поверхности) α.

Так: h_0α – горизонтальный след плоскости (поверхности) α;

f_0α – фронтальный след плоскости (поверхности) α.

12. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает линия, с подстрочным индексом, указывающим принадлежность к линии.

Например: H_a — горизонтальный след прямой (линии) а;

F_a — фронтальный след прямой (линии ) a.

13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами _{1,2,3. n:}

Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом ₀:

14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же буквами, что и натура с добавлением верхнего индекса 0 :

15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :

А 1 0 , В 1 0 , С 1 0 , D 1 0 , .

1 1 0 , 2 1 0 , 3 1 0 , 4 1 0 , .

a 1 0 , b 1 0 , c 1 0 , d 1 0 , .

α 1 0 , β 1 0 , γ 1 0 , δ 1 0 , .

Для облегчения чтения чертежей в учебнике при оформлении иллюстративного материала использованы несколько цветов, каждый из которых имеет определенное смысловое значение: линиями (точками) черного цвета обозначены исходные данные; зеленый цвет использован для линий вспомогательных графических построений; красными линиями (точками) показаны результаты построений или те геометрические элементы, на которые следует обратить особое внимание.

Источник статьи: http://nachert.ru/course/?lesson=1

Какие есть математические символы?

К самым распространённым относятся:

Знак плюс-минус: ±

Знак корня (радикал): √

Факториал: !

Знак интеграла: ∫

Знак возведения в степень: ^ (в типографской и рукописной записи формул не применяется; используется в программировании, наряду с более редкими символами ↑ и **, а также в «линейной» текстовой записи формул).

Как напечатать римские цифры на клавиатуре?

Для написания римских цифр необходимо изменить раскладку клавиатуры на английскую (клавиши alt и shift в левой части клавиатуры необходимо нажать одновременно) и использовать в качестве цифр буквы I (русская клавиша “Ш”), V (русская клавиша “М”), X (русская клавиша “Ч”), M (русская клавиша “Ь”).

Что обозначает этот знак ))))) в переписке?

Скобочки в переписках обозначают степень улыбки пользователя, который их отправляет. То есть одна скобочка это просто “доволен”, две чуть больше “доволен”, три уже смех и далее подразумевается, что пользователь очень сильно смеётся, но обычно, всё это не работает и скобки ставят просто по привычке.

Какие числа называют целыми?

Целые числа это – множество натуральных чисел (1,2,3,4. n); чисел, противоположных натуральным (-1,-2,-3,-4. -n) и ноль (0).
Иными словами, это числа, не имеющие дробную часть.
Например:
24; 68; 4512; 25687 – все целые (все натуральные числа)
35; -98; 0; -645; 8830 – все целые ( натуральные только 35 и 8830)
654,25; 0,78; -656,4587 – все нецелые (натуральных нет)

Чему равно число Пи?

Никто не знает точно, чему равно пи. Если разделить длину окружности на ее диаметр, то результат всегда будет одинаковый, какую окружность ни возьми. Этот результат и обозначили греческой буквой пи. Буква понадобилась потому, что привычными цифрами это число точно записать невозможно. Но мы знаем, чему оно равно приблизительно.

Самое знаменитое приближение – 3,14. Чтобы запомнить больше цифр, можно выучить стишок:

Источник статьи: http://yandex.ru/q/question/hw.math/kakie_est_matematicheskie_simvoly_361b186d/

Какие есть математические символы?

К самым распространённым относятся:

Знак плюс-минус: ±

Знак корня (радикал): √

Факториал: !

Знак интеграла: ∫

Как напечатать римские цифры на клавиатуре?

Что обозначает этот знак ))))) в переписке?

Какие числа называют целыми?

Какие интересные логические и математические парадоксы вы знаете? Можете ли вы их объяснить «на пальцах»?

Каждое второе натуральное число делится на два, каждое третье-на три, каждое четвертое-на четыре. Казалось бы царит полная гармония. Но откуда берется беспорядок с простыми числами(которые делятся сами на себя и единицу)? Вот почему говорят, что хаос это непознанная закономерность.

Чему равно число Пи?

Самое знаменитое приближение – 3,14. Чтобы запомнить больше цифр, можно выучить стишок:

Источник статьи: http://yandex.ru/q/question/hw.math/kakie_est_matematicheskie_simvoly_361b186d/?answer_id=fa09831f-99aa-47a7-b85d-ceee64e65d87

Источник

Символьные обозначения

Символьные обозначения, все их многообразие, может быть подразделено на две группы:
— Первая группа — обозначения геометрических фигур и отношения между ними;
— Вторая группа — обозначения логических операций, составляющая синтаксическую основу геометрического языка.

Символьные обозначения — Первая группа

Символы, обозначающие геометрические фигуры и отношения между ними

Обозначения геометрических фигур:
Φ — геометрическая фигура;
A, B, C, D, …, L, M, N, … — точки расположенные в пространстве;
1, 2, 3, 4, …, 12, 13, 14, … — точки расположенные в пространстве;
a, b, c, d, …, l, m, n, … — линии, произвольно расположенные по отношению к плоскостям проекций;
h, υ(f), ω — линии уровня (горизонталь, фронталь, профильная прямая соответственно);
(AB) — прямая проходящая через точки A и B;
[AB) — луч с началом в точке A;
[AB] — отрезок прямой, ограниченный точками A и B;
α, β, γ, δ, …, ζ, η, θ — поверхность;
∠ABC — угол с вершиной в точке B;
∠α, ∠β, ∠γ — угол α, угол β, угол γ соответственно;
|AB| — расстояние от точки A до точки B (длина отрезка AB);
|Aa| — расстояние от точки A до линии a;
|Aα| — расстояние от точки A до поверхности α;
|ab| — расстояние между прямыми a и b;
|αβ| — расстояние между поверхностями α и β;
H, V, W — координатные плоскости проекций (именуемые как горизонтальная, фронтальная, профильная соответственно);
П₁, П₂, П₃ — координатные плоскости проекций (именуемые как горизонтальная, фронтальная, профильная соответственно);
x, y, z — координатные оси проекций (ось абсцисс, ось ординат, ось аппликат);
k_o — постоянная прямая эпюра Монжа;

O — точка пересечения осей проекций;
`, «, `» — верхние индексы для проекций точек, прямых, углов, фигур, поверхностей на плоскости проекций (именуемые как горизонтальную, фронтальную, профильную соответственно);
1, 2, 3 — верхние индексы для проекций точек, прямых, углов, фигур, поверхностей на плоскости проекций (именуемые как горизонтальную, фронтальную, профильную соответственно);
α_H, α_V, α_W — след поверхности оставляемый на горизонтальной, на фронтальной, на профильной плоскости проекций соответственно;

α_H, α_V, α_W — след поверхности α оставляемый на горизонтальной, на фронтальной, на профильной плоскости проекций соответственно;

a_H, a_V, a_W — след прямой a оставляемый на горизонтальной, на фронтальной, на профильной плоскости проекций соответственно;

Проекции точек, линий, поверхностей любой геометрической фигуры обозначаются теми же буквами (или цифрами), что и оригинал, с добавлением верхнего индекса A`, A», A`»
или 1`, 1″, 1`», соответствующего плоскости проекции, на которой они получены:
A`, B`, C`, D`, …, L`, M`, N`, … — горизонтальные проекции точек;
A», B», C», D», …, L», M», N», … — фронтальные проекции точек;
A`», B`», C`», D`», …, L`», M`», N`», … — профильные проекции точек;
a`, b`, c`, d`, …, l`, m`, n`, … — горизонтальные проекции линий;
a», b», c», d», …, l», m», n», … — фронтальные проекции линий;
a`», b`», c`», d`», …, l`», m`», n`», … — профильные проекции линий;
α`, β`, γ`, δ`, …, ζ`, η`, θ`, … — горизонтальные проекции поверхностей;
α», β», γ», δ», …, ζ», η», θ», … — фронтальные проекции поверхностей;
α`», β`», γ`», δ`», …, ζ`», η`», θ`», … — профильные проекции поверхностей;

Символы взаиморасположения геометрических объектов

Обозначение	Смысловое значение	Пример символической записи
(…)	способ задания геометрического объекта в пространстве и на комплексном чертеже	А(А`, А») – точка А задана на комплексном чертеже горизонтальной и фронтальной проекциями; α(А, b) – плоскость α задана прямой b и точкой А.
∈ ⊂ , ⊃	принадлежность	А∈l – точка А принадлежит прямой l; l⊂α – прямая l лежит в плоскости α
≡	совпадение	А`≡ В` – горизонтальные проекции точек А и В совпадают.
‖ , //	параллельность	a // b – прямые a и b параллельны.
⊥	перпендикулярность	c⊥d – прямые c и d перпендикулярны.
∸	скрещивание	m ∸ n – прямые m и n скрещивающиеся.
∩	пересечение	k ∩ l – прямые k и l пересекаются.
∾	подобие	ΔАВС ~ ΔDEF – треугольники ABC и DEF подобны.
≅	конгруэнтность	ΔАВС ≅ /АВ/ = /CD/ – отрезки АВ и CD равны.
=	равенство, результат действия	/АВ/ = /CD/ – длины отрезков AB и CD равны; k ∩ l = M — прямые k и l пересекаются в точке M.
/	отрицание	А ∉ l – точка А не принадлежит прямой l.
→ ←	отображение, преобразование	V/H → V1/H– система ортогональных плоскостей V/H преобразуется в систему плоскостей V1/H

Символьные обозначения — Вторая группа

Символы обозначающие логические операции

∧	конъюнкция предложений (соответствует союзу «и»)	K ∈ a ∧ K ∈ d – точка K принадлежит прямым a и d
∨	дизъюнкция предложений (соответствует союзу «или»)	А ∈ α ∨ A ∉ α – точка А принадлежит плоскости α или точка А не принадлежит плоскости α.
⇒ ⇐	логическое следствие – импликация (следовательно, поэтому)	a // b ∧ c // b ⇒ a // c – прямые а и с параллельны прямой b, следовательно, они параллельны между собой.
⇔	логическая эквивалентность (что то же самое)	A ∈ l ⇔ A` ∈ l`, A» ∈ l» – точка А принадлежит прямой l, следовательно, ее проекции лежат на одноименных проекциях прямой; справедливо и обратное утверждение: проекции точки А лежат на одноименных проекциях прямой l, следовательно, точка принадлежит этой прямой.

Источник

Морфемный разбор слова:

Однокоренные слова к слову:

Обозначения и символика

Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:

группа I — обозначения геометрических фигур и отношений между ними;

группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.

СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ

А. Обозначение геометрических фигур

1. Геометрическая фигура обозначается — Ф.

2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:

Линии уровня обозначаются: h — горизонталь; f— фронталь.

Для прямых используются также следующие обозначения:

(АВ) — прямая, проходящая через точки А а В;

[АВ) — луч с началом в точке А;

[АВ] — отрезок прямой, ограниченный точками А и В.

4. Поверхности обозначаются строчными буквами греческого алфавита:

α(а || b) — плоскость α определяется параллельными прямыми а и b;

5. Углы обозначаются:

6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:

— величина угла АВС;

— величина угла φ.

Прямой угол отмечается квадратом с точкой внутри

7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.

|АВ| — расстояние между точками А и В (длина отрезка АВ);

|Аа| — расстояние от точки А до линии a;

|Аα| — расстояшие от точки А до поверхности α;

|аb| — расстояние между линиями а и b;

|αβ| расстояние между поверхностями α и β.

π₂ —фрюнтальная плоскость проекций.

При замене плоскостей проекций или введении новых плоскостей последние обозначают π₃, π₄ и т. д.

Постояшную прямую эпюра Монжа обозначают k.

Например: H_a — горизонтальный след прямой (линии) а;

F_a — фронтальный след прямой (линии ) a.

13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами _{1,2,3. n:}

15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

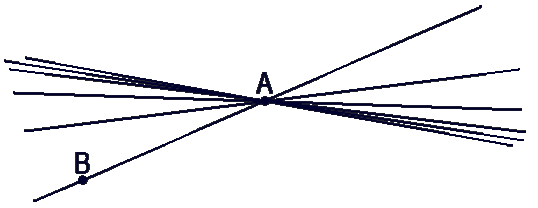
Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

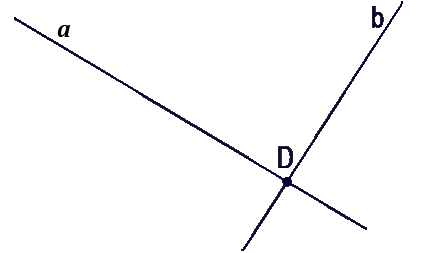
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Как обозначается в геометрии лежит?

Как обозначается в геометрии пересекает?

Теория множеств и теория чисел

Символ TeX (Команда TeX)	Символ (Юникод)	Название
Произношение
(cap)	⋂	Пересечение
«Пересечение … и …», «…, пересечённое с …»
(setminus)		Разность множеств

Как в геометрии обозначаются пересекающиеся прямые?

Говорят, что прямые a и b пересекаются в точке О. Сами прямые называются пересекающимися (a и b – пересекающиеся прямые).

Как в геометрии обозначается точка пересечения?

В тексте пересечение прямых обозначают символом ∩. Информацию на рисунке выше можно записать следующим образом: b ∩ c — прямые b и с пересекаются; a ∩ c — прямые a и с пересекаются.

Как обозначается плоскость в геометрии?

Как отмечается окружность?

Окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности. Это расстояние называется радиус и в записях обозначается буквой R. Центр окружности чаще всего обозначают буквой O. Окружность разделяет плоскость на две части, внутреннюю и внешнюю.

Как в геометрии обозначаются скрещивающиеся прямые?

m ∸ n – прямые m и n скрещивающиеся. k ∩ l – прямые k и l пересекаются.

Как в геометрии обозначаются точки и прямые?

Точки обозначаются большими латинскими буквами, прямые обозначаются малыми латинскими буквами.

Как узнать лежит ли точка на прямой?

Точка принадлежит прямой, если её проекции лежат на одноимённых проекциях этой прямой (рис. 21а). Точка принадлежит плоскости, если она лежит на прямой, лежащей в этой плоскости (рис.

Как показать пересекающиеся прямые?

Чтобы определить на эпюре (комплексном чертеже), пересекаются ли данные прямые в пространстве, достаточно провести линию связи из одной точки пересечения проекций к другой. Если проекции точки пересечения прямых будут лежать на одной линии связи, то прямые пересекаются.

Как называется место пересечения двух плоскостей?

Точка пересечения двух прямых – определение.

Итак, две прямые и на плоскости и в пространстве называются пересекающимися, если они имеют одну общую точку.

Как отмечается в геометрии перпендикуляр?

Перпендикулярность прямых обозначается знаком _|_. На чертежах 53 и 54 АВ_|_DС и DС _|_ АВ. Каждая из этих прямых называется перпендикуляром к другой. АВ — перпендикуляр к СD, и СD — перпендикуляр к АВ.

Как обозначить что прямая лежит в плоскости?

Как обозначить плоскость?

3. Поверхности (плоскости) обозначают строчными буквами греческого алфавита (кроме буквы П): α, β, γ, δ,… 4. Углы обозначают строчными греческими буквами: φ, ψ,…

Как определить плоскость?

Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки; Две плоскости являются либо параллельными, либо пересекаются по прямой. Прямая либо параллельна плоскости, либо пересекает её в одной точке, либо находится на плоскости.

Что такое F в геометрии?

Линии уровня обозначаются: h — горизонталь; f— фронталь.

Источник

В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.

Определение и знак подобия в геометрии

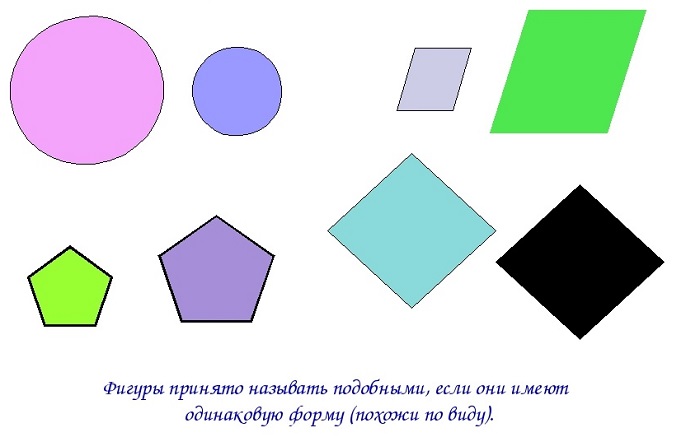
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.

Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:

Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:

1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.

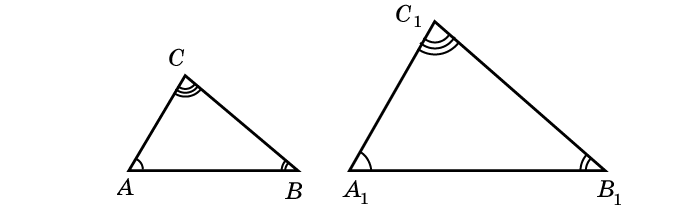
Коэффициент подобия треугольников и знак подобия

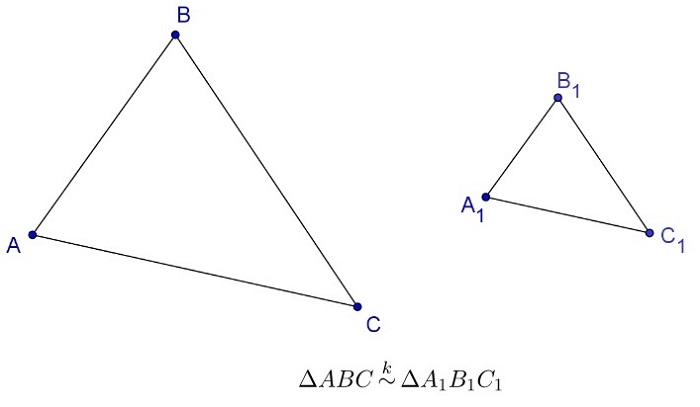
Часто сверху знака подобия выставляют коэффициент подобия треугольников:

В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.

В алгебре высказываний знаком

обозначают логическую операцию «эквиваленция».

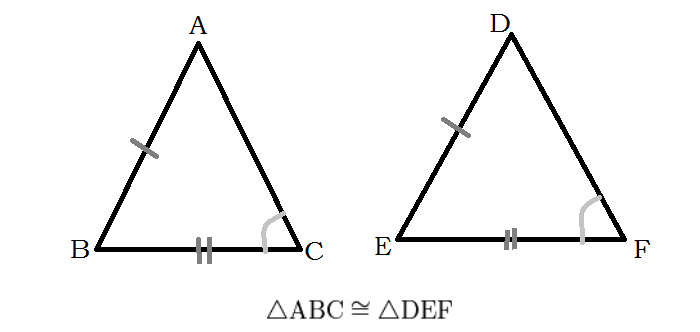
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):

Признаки подобия прямоугольных треугольников

Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.

Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.

Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.

треугольник ∆ABC и треугольник ∆A₁B₁C₁ считаются подобными при равнозначности углов и пропорциональности сторон;

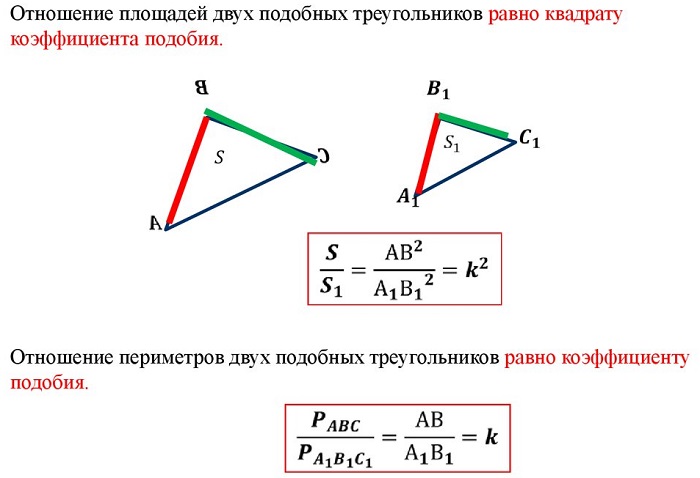
отношение площадей подобных треугольников равно квадрату коэффициента подобия.

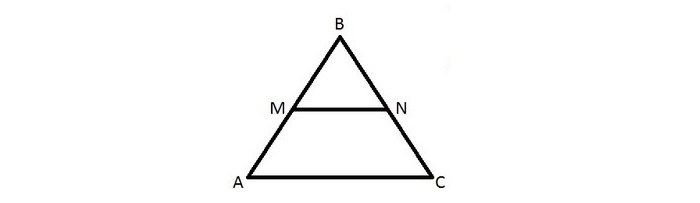
Доказательство подобия треугольников через среднюю линию

Требуется доказательство подобия треугольников ∆MBN и ∆ABC.

Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:

Отсюда делаем вывод, что ∆MBN

∆ABC по II признаку подобия треугольников, что и требовалось доказать.

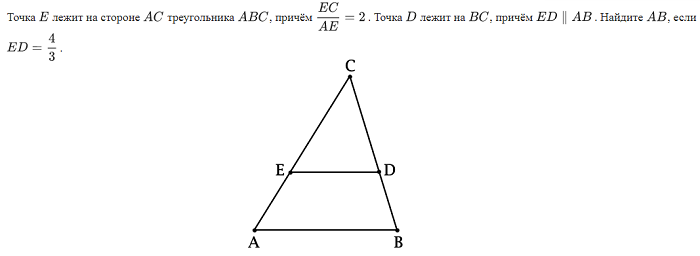
Примеры решения задач по геометрии на тему «Подобие треугольников»

Источник

Теперь вы знаете какие однокоренные слова подходят к слову Как в геометрии пишется знак лежит, а так же какой у него корень, приставка, суффикс и окончание. Вы можете дополнить список однокоренных слов к слову «Как в геометрии пишется знак лежит», предложив свой вариант в комментариях ниже, а также выразить свое несогласие проведенным с морфемным разбором.

Источник

Что такое плоскость

Мы думаем, что вы уже знаете значение слова «плоскость» из уроков геометрии. Возможно, вы слышали его, но плохо представляете, что это такое. Также с этим понятием мы сталкиваемся и в нашей обычной, нематематической жизни. Подумайте, какой предмет мы называем плоским. Верно: тот, который не имеет объема и включает в себя только два измерения — длину и ширину. Любители комиксов, манги и компьютерных игр точно знают понятие «2D», которое ставят в противовес объемному, современному «3D».

Если прошлый абзац был вам совсем непонятен, следующий пример исправит ситуацию. Представьте себе лист бумаги, поверхность пола, стен или стола. В данном случае мы можем убрать слово «поверхность» и заменить его на «плоскость», но будет один нюанс. Площадь этих предметов ограниченна, в то время как плоскость бесконечна, не имеет каких-либо краев или границ.

Итак, пришло время сформулировать определение плоскости:

Плоскость — это поверхность, которая содержит прямые, соединяющие две любые ее точки.

В другом источнике определение плоскости звучит так:

Плоскость — поверхность, имеющая два измерения.

Советуем запомнить обе формулировки, так как первая подсказывает нам некоторые свойства плоскости — их мы обсудим чуть позже. Вторая же дает нам понять суть этого слова.

Плоскость — это одно из фундаментальных, т. е. основных, понятий в геометрии наряду с точкой и прямой. Можно сказать, что эти три слова связаны друг с другом, как лучшие друзья, и у них множество совместных «историй». Ни одна аксиома, теорема или другое геометрическое понятие не существует отдельно от этих трех.

Из плоскостей математики собирают объемные фигуры. Так, куб состоит из 6 граней, каждая из которых представляет собой часть отдельной плоскости. По этому же принципу мы можем сказать, что правильная пирамида состоит из 4 таких частей, а четырехугольная пирамида — из 5. Кстати, раздел геометрии, который изучает фигуры на плоскости, называется планиметрия, а изучающий объемные фигуры — стереометрия.

Как обозначается плоскость

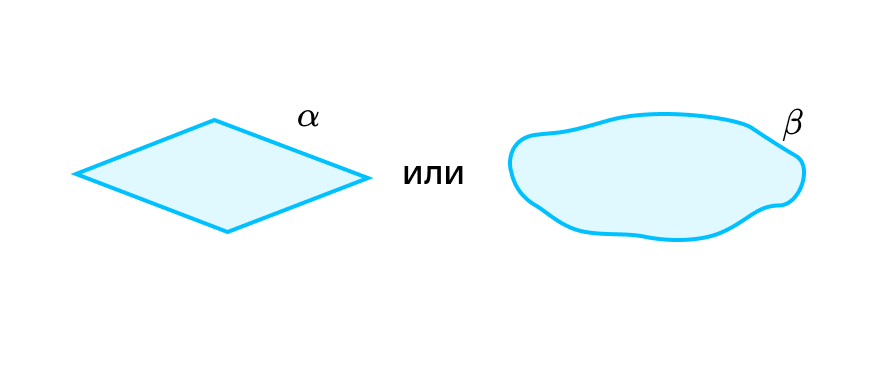
На уроках геометрии вы будете часто рисовать плоскости и решать связанные с ними задачи. На чертеже плоскость чаще всего изображают в виде параллелограмма или произвольной замкнутой области. Для обозначения плоскости используют строчные буквы греческого алфавита — α, β, γ и т. д.:

Вот мы и узнали, что такое плоскость в математике. Идем дальше!

Какие бывают виды плоскостей

Самым любопытным из вас может стать интересно, все ли плоскости одинаковые и какие бывают виды плоскостей. Ответы на эти вопросы вы обязательно получите в вузе на предмете начертательная геометрия, если выберете математический профиль. Но ждать придется долго, а ответ хочется получить сейчас, поэтому мы немного приоткроем завесу тайны.

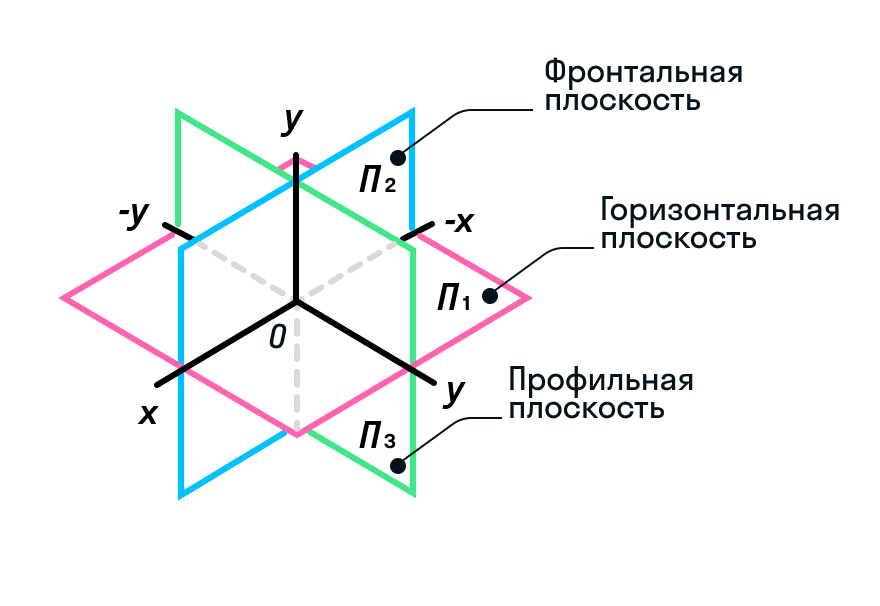
На рисунке показаны три вида плоскостей в трехмерном пространстве, которое еще называют xyz по трем координатным осям.

Горизонтальная плоскость — это та плоскость, которой принадлежит ось Ox, расположенная горизонтально.

Фронтальная плоскость — это плоскость, которая расположена вертикально перед зрителем.

Профильная плоскость — это плоскость, расположенная вертикально и пересекающаяся под прямым углом с горизонтальной и фронтальной.

Повторим, что такая классификация — это лишь дополнительный материал для самых любопытных математиков, им можно удивить учителя или взять его на самостоятельное исследование или даже научный проект.

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Как плоскость и точка могут располагаться относительно друг друга

Чтобы было проще понять, давайте сравним плоскость и точку с вами и вашим домашним питомцем. Вы можете или находиться вместе в одной комнате, или быть раздельно, не видеть друг друга. Этот пример наглядно показывает взаимоотношения прямой и плоскости: точка может принадлежать плоскости, а может и не принадлежать ей.

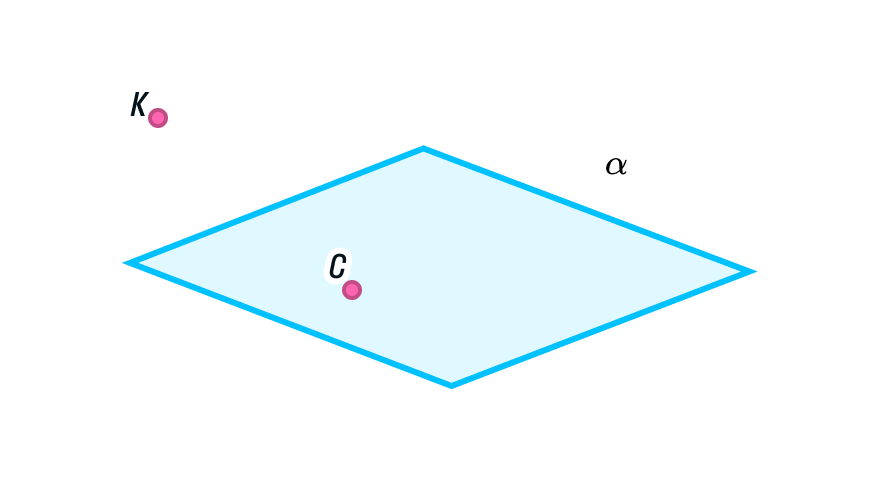
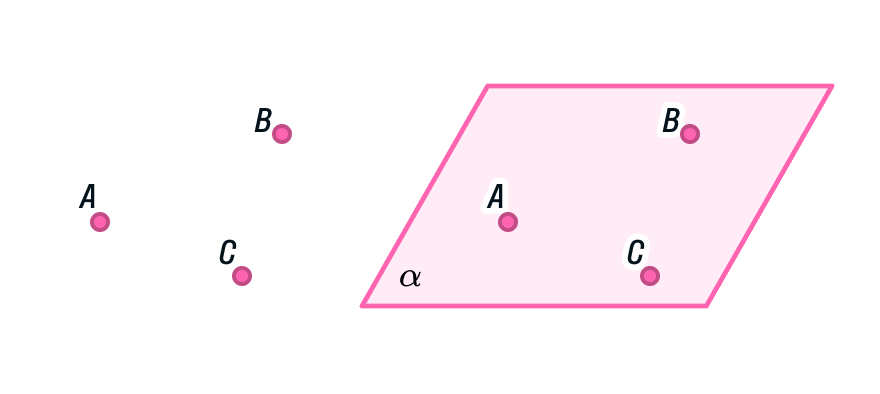
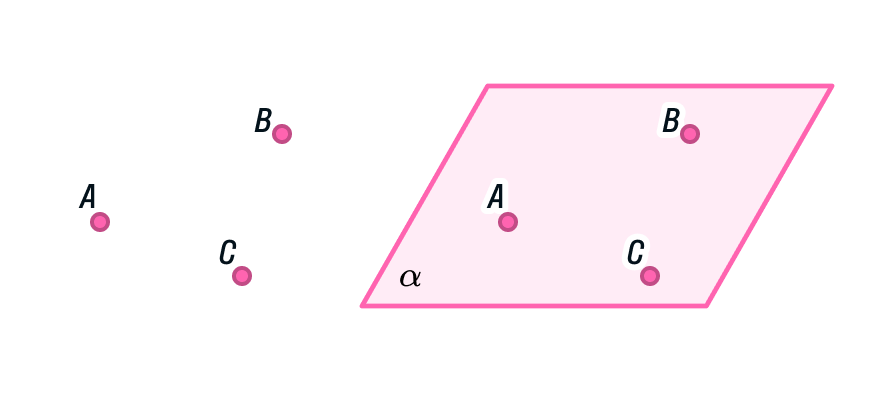
Допустим, в плоскости α есть точка С. Тогда мы можем записать это так: C ∈ α. Возьмем другую точку K, которая лежит вне плоскости. Для записи этой информации используем другой знак — ∉: K ∉ α, иными словами, точка K не принадлежит плоскости α.

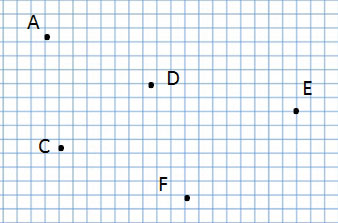
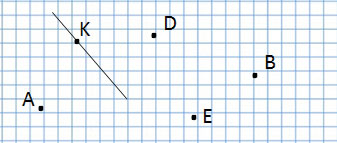
Проверьте себя!

Внимательно рассмотрите рисунок и скажите, какие точки принадлежат плоскости, а какие нет.

Чтобы узнать больше о том, как располагаются точки и плоскости относительно друг друга, нам нужно познакомиться с тремя аксиомами.

Аксиома 1.

В каждой плоскости имеются точки.

Представьте себе бескрайний пляж с бесконечным множеством песчинок. Подобно ему, любая плоскость имеет множество точек, даже если они не обозначены на рисунке.

Аксиома 2.

Через три точки, не лежащие на одной прямой, проходит плоскость, причем только одна.

Эту аксиому можно считать способом задать плоскость в пространстве. Вы и сами можете это сделать — просто поставьте на листе бумаги три точки: M, L и N. Поздравляем, только что вы задали через них новую плоскость, которую можно назвать в честь этих точек, — плоскость MLN. Усложним задачу: теперь с помощью фломастера поставьте пару точек на полу и одну на стене. Вуаля, новая плоскость готова! Только не забудьте стереть ваш чертеж до прихода родителей.

Кстати, последний эксперимент наталкивает на мысль о том, что плоскость необязательно должна быть ровной, параллельной полу, стенам и так далее. Она вполне может располагаться под углом.

Аксиома 3.

Имеются по крайней мере четыре точки, не лежащие в одной плоскости.

Эта аксиома подтверждает тот факт, что точка может и не принадлежать плоскости. Если мы вернемся к нашему чертежу на бумаге, мы можем поставить еще одну точку на листе. В таком случае эта новая точка будет принадлежать плоскости. Если же мы поставим ее на доске, оконном стекле, подошве своего ботинка, точка не будет принадлежать исходной плоскости.

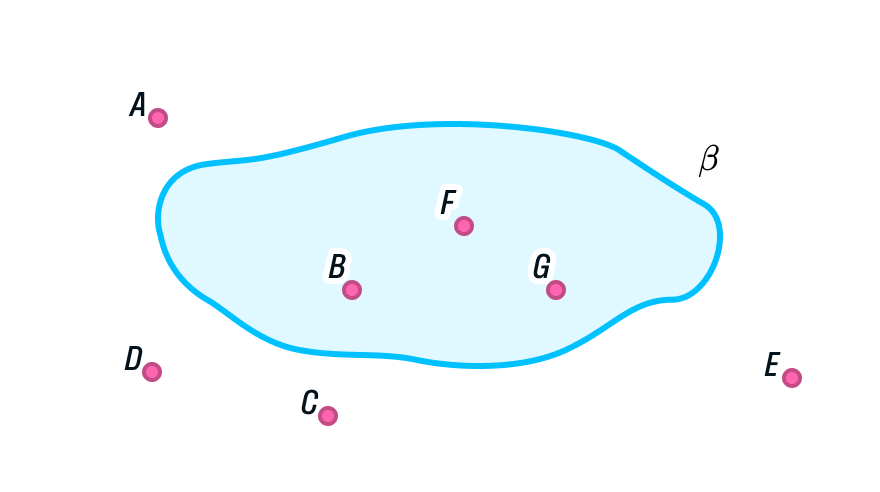
Также множество точек может одновременно принадлежать разным плоскостям в пространстве. Предположим, у нас есть точки A, B, C и D. Давайте узнаем, какие плоскости могут проходить через них.

Как прямая и плоскость могут располагаться относительно друг друга в пространстве

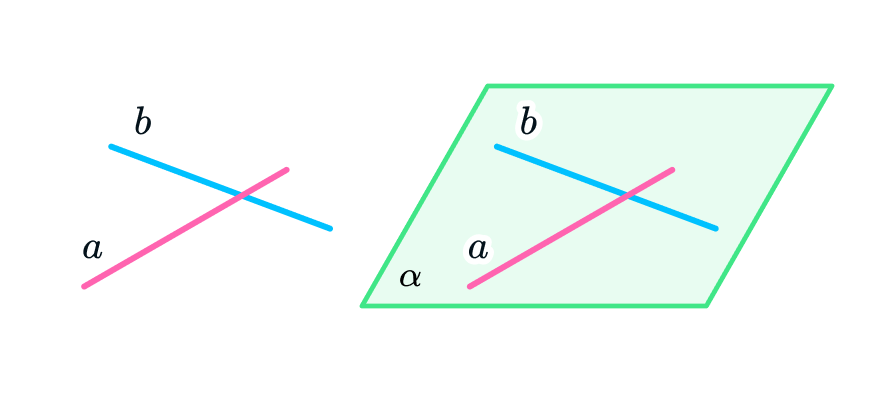
Есть несколько вариантов, как плоскость и прямая или луч могут взаимно располагаться в пространстве. Давайте разберем подробно каждый из них.

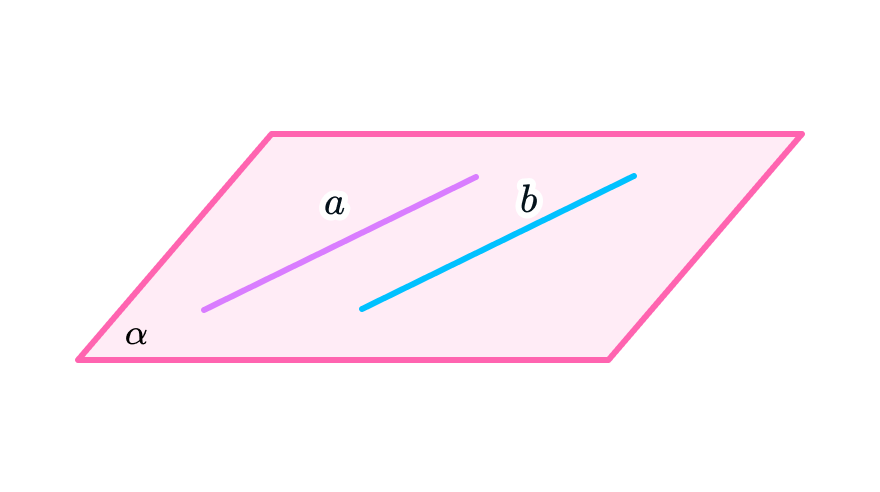
1. Прямая может лежать в плоскости

Здесь все просто. А если на уроках геометрии вы захотите похвастаться своими знаниями, можно добавить: «Если в плоскости лежат хотя бы две точки, которые принадлежат прямой, эта прямая лежит в плоскости». Учитель точно будет в восторге!

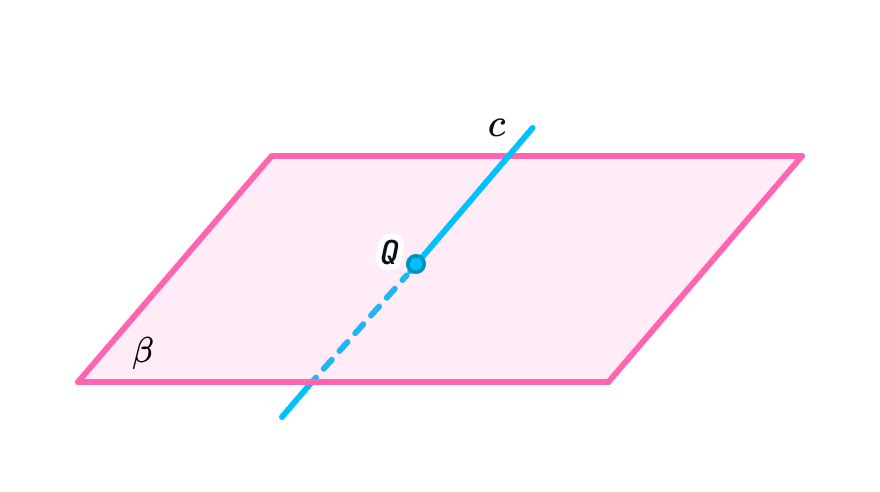
2. Прямая может пересекать плоскость

Проведем эксперимент: возьмем плоскость в пространстве (кружочек колбасы) и пересечем ее насквозь прямой (зубочисткой). Посчитайте, сколько общих точек они будут иметь. Верно, только одну.

В математике пересечение обозначают символом ⋂. Так, c ⋂ β = V означает, что прямая c пересекает плоскость β в точке V.

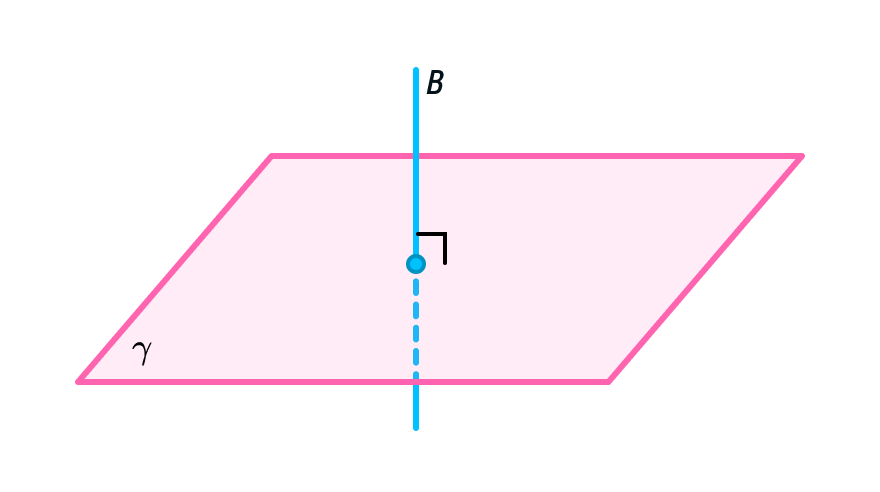
Из опыта с колбасой ясно, что мы можем воткнуть зубочистку разными способами, т. е. под разным углом. Исходя из этого, в геометрии есть понятие угла между прямой и плоскостью, где отдельно отмечается случай перпендикулярности.

Прямая, перпендикулярная к плоскости, — это прямая, перпендикулярная любой прямой, которая лежит в плоскости.

Если прямая B перпендикулярна плоскости γ, это можно записать следующим образом: В ⟂ γ.

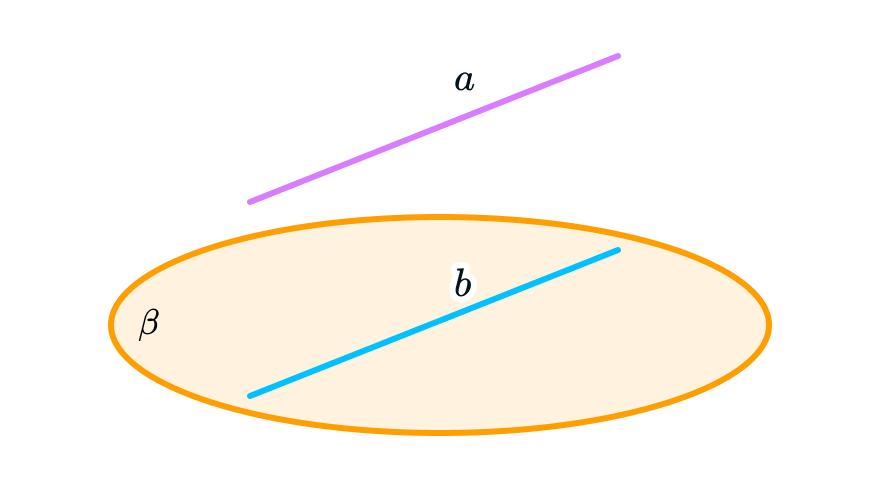
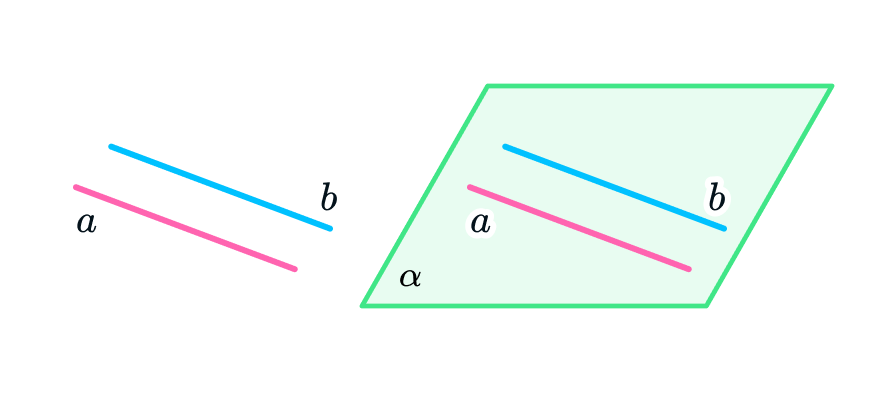
3. Прямая может быть параллельна плоскости

В таком случае прямая и плоскость не будут иметь общих точек. Если прямая D параллельна плоскости γ, это можно записать следующим образом: D || γ.

Подведем краткий итог с помощью таблицы.

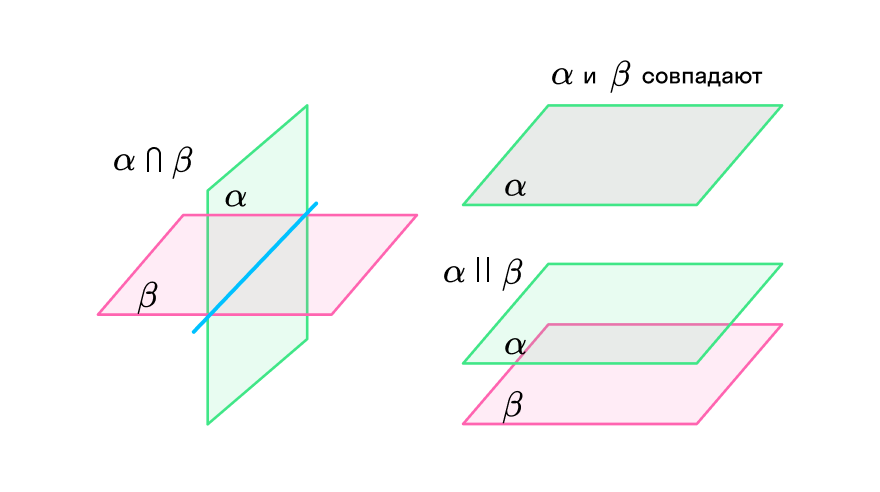
Как две плоскости могут располагаться относительно друг друга

Следующий пункт нашего обсуждения — это взаимное расположение плоскостей. Прежде чем продолжить читать, остановитесь на секунду и подумайте сами, как могут располагаться в пространстве две плоскости.

Да, вы абсолютно правы! Плоскости могут:

быть параллельны друг другу;
пересекаться, в том числе под углом 90 градусов (в таком случае плоскости могут называться перпендикулярными);
совпадать друг с другом (иметь по крайней мере 3 общие точки).

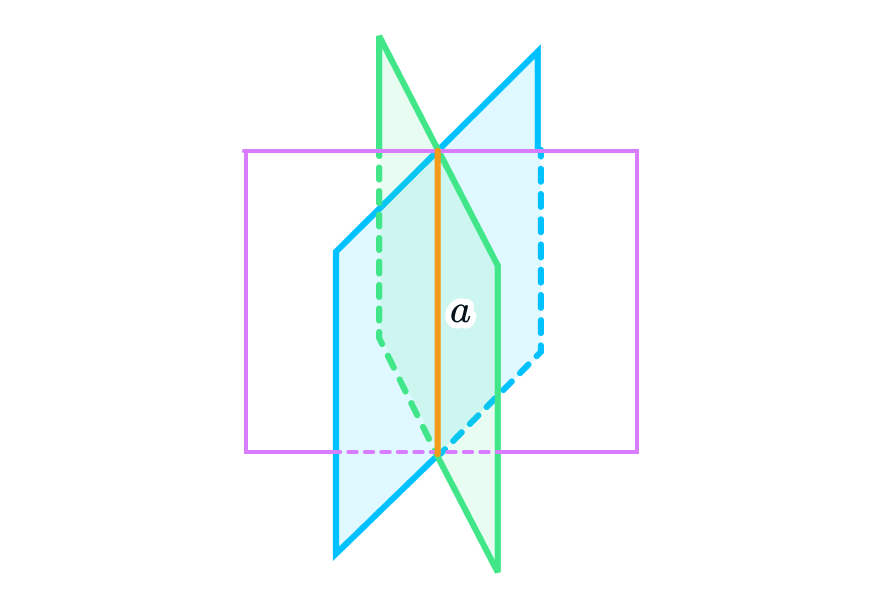
Кстати, это еще не все типы расположений. Дело в том, что множество плоскостей могут пересекаться в одной точке или по одной прямой, но об этом мы расскажем в других статьях. Оставайтесь вместе с нами

Как задать плоскость в пространстве

На уроках геометрии учитель может спросить: «А каким образом можно задать плоскость?», и некоторые из ваших одноклассников растеряются. Давайте разберемся, что значит «задать плоскость». По сути, это значит перечислить элементы и способы их расстановки, которые позволяют сказать: «Вот, через них проходит плоскость». Теперь подробнее разберемся, в каких случаях можно утверждать, что плоскость существует.

Вернемся к аксиоме. Как мы уже знаем, через три точки, не лежащие на одной прямой, проходит плоскость, причем только одна. А значит, задать плоскость можно через три точки, которые не лежат на одной прямой.
Второй способ вытекает из первого: проведем прямую, соединяющую две точки из трех. Сейчас нашей плоскости принадлежат прямая и точка, не лежащая на ней. Они и задают плоскость.
Продолжим соединять точки. На этот раз соединим между собой любые две точки: пусть это будут А и В, А и С. Мы получим две прямые, которые пересекаются друг с другом. Это значит, что плоскость могут задать две пересекающиеся прямые.
Четвертый способ: плоскость могут задать прямые, параллельные друг другу.

На курсах по профильной математике в школе Skysmart вы познакомитесь с еще более увлекательными темами, получите необходимые сведения для подготовки к контрольным и почувствуете себя настоящим ученым. Ждем вас на занятиях, до скорых встреч!

Источник

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне
просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так
и не пришли к единому определению.

Запомните!

Точка — элементарная фигура, не
имеющая частей.

Прямая состоит из множества
точек и простирается бесконечно
в обе стороны.

На рисунке изображена прямая a и точки D, F, G и
H. Точки F и G
лежат на прямой a.
Точки D и H
не
лежат на прямой a.

В тексте точку обозначают символом «(·)».
Принадлежность и непринадлежность точки
прямой обозначают символами «∈» и «∉». Знак принадлежности можно запомнить как
зеркальное отображение буквы «Э» или как знак евро «€» .

(·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a);
(·)G ∈ a — точка G принадлежит прямой a;
(·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a);
(·)H ∉ a — точка H не принадлежит прямой a.

Как обозначить прямую

Прямую обычно обозначают одной
маленькой латинской буквой.

Прямую, на которой отмечены
две точки, иногда обозначают
по названиям этих точек большими латинскими точками.

Прямая a
Прямая f
Прямая CH
Прямая DK

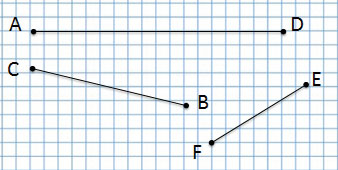
Точки D, E и F — лежат на одной прямой, поэтому:
прямая DE,
прямая EF и
прямая DF —
это три разных имени одной и той же прямой.

Разбор примера

Проведите прямую, обозначьте её буквой a и
отметьте точки A и B, лежащие на этой прямой, и
точки P, Q и R, не лежащие на ней. Опишите
взаимное расположение точек A, B, P, Q, R и
прямой a, используя символы ∈ и ∉.

Решение задачи

Проведём прямую.

Обозначим её буквой a.

Отметим точки (·)A и (·)B, лежащие на прямой a.

Отметим точки (·)P, (·)Q и (·)R, не лежащие на прямой a.

Опишем взаимное расположение точек и прямой.

(·)A ∈ a
(·)B ∈ a
(·)P ∉ a
(·)Q ∉ a
(·)R ∉ a

Задача решена.

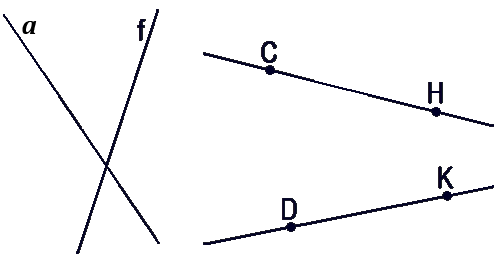
Как обозначается пересечение прямых

На рисунке прямые a и b
не пересекаются.

Прямые b и
c пересекаются.

Хотя на чертеже не видно, но прямые a и
c тоже пересекаются (это становится ясно, если мысленно
продолжить вниз прямые a и с).

В тексте пересечение прямых обозначают
символом ∩. Информацию на рисунке выше можно записать следующим образом:

b ∩ c — прямые b и с пересекаются;
a ∩ c — прямые a и с пересекаются.

Прямые e и g имеют общую точку M.
Другими словами, прямые пересекаются в точке M. Геометрическими обозначениями
пересечение прямых в точке записывается так:
e ∩ g = (·)M

Прямые e и f не имеют общей точки — т.е. они не
пересекаются.

Взаимное расположение прямой и точек

Запомните!

Через любые две точки можно
провести прямую, и притом
только одну.

Через одну точку (·)A можно провести
сколько угодно прямых.

Через две точки
(·)A и (·)B можно провести
только одну прямую.

Сколько общих точек имеют две прямые

Запомните!

Две прямые либо имеют только
одну общую точку, либо не имеют
общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e
нет общих точек, т.к. эти
прямые не пересекаются.

Второй случай расположения прямых

Возможен вариант, что прямые f и e
пересекаются и, значит, имеют одну общую точку (·)M.

Третий случай расположения прямых

Предположим, что прямые
f и e имеют две или больше общих точек.
Например, точки (·)A и (·)B.

Но мы знаем, что через две
точки можно провести только одну прямую. Значит,
прямые f и e совпадают и наше предположение, что
у двух прямых может быть две или более общих точек неверно.

Вывод: две прямые либо имеют только
одну общую точку, либо не имеют
общих точек.

Разбор примера

Проведите три прямые так, чтобы каждые две из
них пересекались. Обозначьте все точки
пересечения этих прямых. Сколько получилось
точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две
прямые пересекались, и обозначим точку
пересечения.

Как мы видим, точка пересечения только одна. Мы
можем провести третью прямую так, чтобы она
тоже проходила через эту точку пересечения.

Теперь прямая a пересекается
с прямой b,
прямая b пересекается с прямой c и
прямая c пересекается с прямой a.

В этом случае
у нас только одна точка
пересечения всех прямых — точка (·)D.

Но возможен и другой вариант. Мы можем провести третью прямую c так,
чтобы она не проходила через точку (·)D. Тогда
получится
три точки пересечения — (·)D, (·)E и (·)F.

Прямая a пересекается
с прямой b
в точке (·)D,
прямая b пересекается с прямой c в точке (·)F и
прямая c пересекается с прямой a
в точке (·)E. Условие задачи выполнено.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или
три.

Что такое отрезок

Запомните!

Отрезок —
часть прямой, ограниченная
двумя точками.

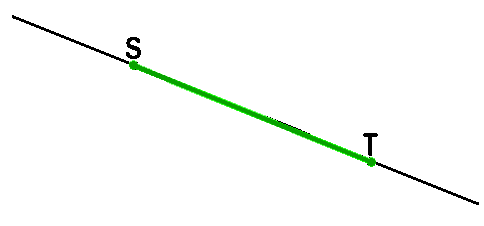
Две точки, ограничивающие отрезок, называются
концами отрезка. У отрезка на рисунке выше концы
называются S и
T.

Сам отрезок можно назвать ST
или TS. Когда изображают отрезок, оставшиеся от
прямой хвосты можно не рисовать.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Содержание

Обозначение геометрических фигур буквами
Точка
Отрезок
Ломаная линия
Многоугольники
Угол
Обозначения и символика
Основы геометрии
Точка
Прямая
Способы обозначения прямых
Способы обозначения лучей
Отрезок
Ломаная
Плоскость, прямая линия, луч
Прямая линия
Обозначение прямой
Некоторые свойства прямой
Обозначение луча
Углы в геометрии
Способы обозначения углов
Виды углов

Обозначение геометрических фигур буквами

В математике есть правило: обозначать геометрические фигуры заглавными буквами латинского алфавита. Сегодня мы научимся этому.

Точка

точка А, точка С, точка D, точка Е и точка F.

Отрезок

отрезок AD, отрезок СВ, отрезок FE

Сколько всего отрезков на данном чертеже?

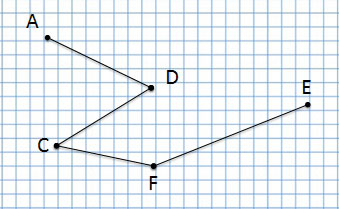
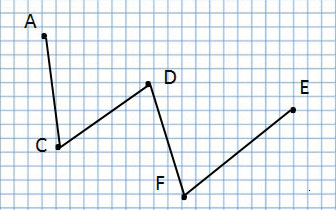
Ломаная линия

А эта ломаная линия совсем по-другому, потому что соединение точек у неё другое:

Ломаная линия ACDFE

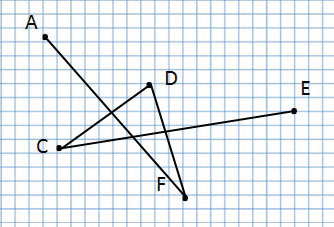
Прочитаю название следующей ломаной линии:

Ломаная линия AFDCE

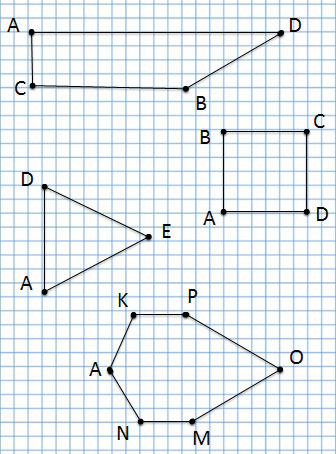
Многоугольники

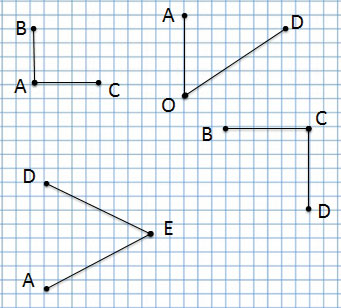
Угол

Угол обозначается тремя буквами. В середине указывается буква, которая обозначает вершину угла.

1 угол: угол BAC или CAB с вершиной А

2 угол: угол AOD или DOA с вершиной О

3 угол: угол AED или DEA с вершиной Е

4 угол: угол BCD или DCB с вершиной С

Поделись с друзьями в социальных сетях:

Источник

Обозначения и символика

Все многообразие обозначений и символов, а также связи между ними могут быть подразделены на две группы:

группа I — обозначения геометрических фигур и отношений между ними;

группа II обозначения логических операций, составляющие синтаксическую основу геометрического языка.

СИМВОЛЫ, ОБОЗНАЧАЮЩИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ

А. Обозначение геометрических фигур

1. Геометрическая фигура обозначается — Ф.

2. Точки обозначаются прописными буквами латинского алфавита или арабскими цифрами:

Линии уровня обозначаются: h — горизонталь; f— фронталь.

Для прямых используются также следующие обозначения:

(АВ) — прямая, проходящая через точки А а В;

[АВ) — луч с началом в точке А;

[АВ] — отрезок прямой, ограниченный точками А и В.

4. Поверхности обозначаются строчными буквами греческого алфавита:

α(а || b) — плоскость α определяется параллельными прямыми а и b;

5. Углы обозначаются:

6. Угловая: величина (градусная мера) обозначается знаком , который ставится над углом:

— величина угла АВС;

— величина угла φ.

Прямой угол отмечается квадратом с точкой внутри

7. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — ||.

|АВ| — расстояние между точками А и В (длина отрезка АВ);

|Аа| — расстояние от точки А до линии a;

|Аα| — расстояшие от точки А до поверхности α;

|аb| — расстояние между линиями а и b;

|αβ| расстояние между поверхностями α и β.

π₂ —фрюнтальная плоскость проекций.

При замене плоскостей проекций или введении новых плоскостей последние обозначают π₃, π₄ и т. д.

Постояшную прямую эпюра Монжа обозначают k.

Например: H_a — горизонтальный след прямой (линии) а;

F_a — фронтальный след прямой (линии ) a.

13. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами _{1,2,3. n:}

15. Вторичные проекции обозначаются путем добавления верхнего индекса 1 :

Источник

Основы геометрии

Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.

Познакомимся с основными геометрическими понятиями, изучаемыми в начальной школе.

Точка

Точка — это основная и самая простая геометрическая фигура.

В геометрии точка обозначается заглавной латинской буквой или цифрой. Многие латинские буквы по написанию похожи на английские буквы.

В тексте точку обозначают следующим символом: « (·) A » — точка « А ».

Прямая

Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.

Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.

Способы обозначения прямых

Способы обозначения лучей

Отрезок

Основное свойство отрезка — это его длина.

Длина отрезка — это расстояние между его концами.

В математике отрезок обозначается заглавными латинскими буквами.

Ломаная

Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.

Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.

Звенья ломаной — это отрезки ломаной.

В математике ломаная обозначается заглавными латинскими буквами.

Чтобы найти длину ломаной, необходимо сложить длины всех её звеньев (отрезков), из которых она состоит.

KLCM = KL + LC + CM = 3 см + 2 см + 2 см = 7 см

Вот мы и познакомились с основами геометрии. Теперь мы готовы рассмотреть не менее важную геометрическую фигуру — угол.

Источник

Плоскость, прямая линия, луч

Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.

Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.

Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.

Плоскость нельзя измерять, потому что она бесконечная.

Плоскость нельзя согнуть, в каком бы положении она ни находилась.

Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.

Прямая линия

Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.

Обозначение прямой

Например, на рисунке 1 обозначены такие прямые:

Рис. 1 Обозначение прямой линии

Рис. 2 Обозначение прямой с несколькими точками

Некоторые свойства прямой

Две точки, лежащие на одной прямой, создают отрезок этой прямой.

Через две любые точки на плоскости можно провести единственную прямую.

Рис. 3 Отрезок на прямой

Две разные прямые могут пересекаться или не пересекаться.

Две прямые пересекаются в том случае, если у них есть общая точка.

Рис. 5 Пересечение прямых

Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.

Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.

Рис. 6 Деление прямой линии точкой

У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.

Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.

Обозначение луча

Луч, как и прямую, обозначают двумя способами.

Рис. 7 Обозначение луча

На рисунке 2 приведены примеры обозначения луча:

Луч имеет второе название – полупрямая.

Рис. 8 Дополнительные друг другу и совпадающие лучи

На рисунке 8 видно, что:

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.6 / 5. Количество оценок: 18

Источник

Углы в геометрии

Угол — это геометрическая фигура, которая состоит из двух лучей и вершины.

Вершина угла — это точка, в которой два луча берут начало.

Стороны угла — это лучи, которые образуют угол.

Например: Вершина угла — точка « O ».
Стороны угла — « OA » и « OB ».

Для обозначения угла в тексте используется символ: AOB

Способы обозначения углов

Одной заглавной латинской буквой, указывающей его вершину.

Угол: O

Тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

Угол: AOD

Называть угол можно с любого края, но НЕ с вершины.

При таком обозначении вершина угла должна всегда находиться в середине названия.

Единица измерения углов — градусы. Углы измеряют с помощью специального прибора — транспортира.

Для обозначения градусов в тексте используется символ: °

50 градусов обозначаются так: « 50° »

Виды углов

Вид угла	Размер в градусах	Пример
Прямой	Равен 90°
Острый	Меньше 90°
Тупой	Больше 90°
Развернутый	Равен 180°

Два угла могут иметь одну общую сторону.

Обратите внимание на рисунок ниже. Попробуйте сосчитать и назвать все углы на изображении.

Если насчитали три угла, то вы правы. Давайте их назовём:

Источник

Символьные обозначения

Обозначения и символика

Какие есть математические символы?

Как напечатать римские цифры на клавиатуре?

Что обозначает этот знак ))))) в переписке?

Какие числа называют целыми?

Чему равно число Пи?

Какие есть математические символы?

Как напечатать римские цифры на клавиатуре?

Что обозначает этот знак ))))) в переписке?

Какие числа называют целыми?

Какие интересные логические и математические парадоксы вы знаете? Можете ли вы их объяснить «на пальцах»?

Чему равно число Пи?

Символьные обозначения

Обозначения и символика

Геометрия 7 класс.Точка, прямая и отрезок

Как обозначить прямую

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Как обозначается пересечение прямых

Взаимное расположение прямой и точек

Сколько общих точек имеют две прямые

Первый случай расположения прямых

Второй случай расположения прямых

Третий случай расположения прямых

Задача № 3 из учебника Атанасян 7-9 класс

Решение задачи

Что такое отрезок

Как обозначается в геометрии лежит?

Как обозначается в геометрии пересекает?

Как в геометрии обозначаются пересекающиеся прямые?

Как в геометрии обозначается точка пересечения?

Как обозначается плоскость в геометрии?

Как отмечается окружность?

Как в геометрии обозначаются скрещивающиеся прямые?

Как в геометрии обозначаются точки и прямые?

Как узнать лежит ли точка на прямой?

Как показать пересекающиеся прямые?

Как называется место пересечения двух плоскостей?

Как отмечается в геометрии перпендикуляр?

Как обозначить что прямая лежит в плоскости?

Как обозначить плоскость?

Как определить плоскость?

Что такое F в геометрии?

Определение и знак подобия в геометрии

Коэффициент подобия треугольников и знак подобия

Признаки подобия прямоугольных треугольников

Доказательство подобия треугольников через среднюю линию

Примеры решения задач по геометрии на тему «Подобие треугольников»

Что такое плоскость

Как обозначается плоскость

Какие бывают виды плоскостей

Как плоскость и точка могут располагаться относительно друг друга

Как прямая и плоскость могут располагаться относительно друг друга в пространстве

Как две плоскости могут располагаться относительно друг друга

Как задать плоскость в пространстве

Как обозначить прямую

Разбор примера

Решение задачи

Как обозначается пересечение прямых

Взаимное расположение прямой и точек

Сколько общих точек имеют две прямые

Первый случай расположения прямых

Второй случай расположения прямых

Третий случай расположения прямых

Разбор примера

Решение задачи

Что такое отрезок

Обозначение геометрических фигур буквами

Точка

Отрезок

Ломаная линия

Многоугольники

Угол

Обозначения и символика

Основы геометрии

Точка

Прямая

Способы обозначения прямых

Способы обозначения лучей

Геометрия 7 класс.
Точка, прямая и отрезок