9
Сказка по математике «Дроби близнецы»
Сказка по математике
«Дроби близнецы.»
Автор-ученица 6-а класса МБОУ СОШ №18 г. Брянска Атанова Виктория.
Учитель- Завадская Елена Владимировна
Аннотация— Сказка по теме обыкновенные дроби. В сказке рассказывается об основном свойстве дроби и о том, что одну и туже дробь можно записать по -разному.
Жили- были три дроби-подружки 1/3, 3/9 и 4/12.Они всегда жили по соседству, проводили много времени вместе, делились секретами и очень дорожили своей дружбой. Когда-то давно их родители переехали в другую страну . Историю своей семьи подружки не знали. Дроби- подружки любили отмечать вместе праздники . И вот как-то на Новый год 1/3 , 4/12 и 3/9 собрались все вместе в загородном доме, куда пригласили своих друзей –знаки действий, другие обыкновенные дроби, десятичные дроби и любимую крёстную ОСНОВНОЕ СВОЙСТВО ДРОБИ.
Подружки обменялись подарками по старой традиции и с нетерпением ждали что же подарит крёстная ( её подарки всегда были очень неожиданными и запоминались на всю жизнь).
И вот часы пробили 12 часов и наступил этот волшебный час. Крёстная сказала: « Слушайте все дроби! У каждой из вас есть числитель и знаменатель. Если числитель и знаменатель дроби умножить или разделить на одно и тоже число, то значение дроби от этого не изменится!» . Ещё крёстная сказала, что это правило применяют для сокращения дробей и если числитель и знаменатель нельзя разделить ни на какое число, то такая дробь называется несократимой.
Все были поражены, когда преобразовав дроби :
3/9=1/3 ( разделили числитель и знаменатель на 3)
4/12=1/3 (разделили числитель и знаменатель на 4) ,а 1/3 оказалась несократимой дробью,
поняли, что дроби-подружки на самом деле дроби-близняшки! Сколько было радости веселья и счастья.
Дроби стали ещё больше дружить и рассказали секрет крёстным и другим дробям, которые тоже смогли найти своих родных.
Автор материала: В. Атанова (6 класс)
Опубликовано 22.06.18 в 18:20 в группе «Детское творчество»

Комментарии (2)
Алла Евгеньевна Гордеева, 25.06.18 в 11:42
1Ответить Пожаловаться
Спасибо, Елена Владимировна, за ценный материал, который всегда актуален.
Заинтересовать — полдела сделать!
Чтобы написать комментарий необходимо авторизоваться.
Создание математической сказки-один из самых интересных для детей видов творчества, который позволяет привить вкус к самостоятельным рассуждениям, способствует развитию математического мышления и стимулирует мыслительный процесс Математическая сказка является средством прочного усвоения математического понятия. Ее можно использоватьв закреплении узученной темы,при повторении.
Презентация, создана учеником 6 класса-Космодемьянским Михаилом, который в увлекательной и красочной форме рассказывает об основном свойстве дробей- сокращении дробей и советует изучать их свойства
Слайд 1Муниципальное бюджетное общеобразовательное учреждение лицей № 3 г. Воронеж Презентация на тему: «Математическая сказка про дроби» Выполнил: ученик 6 «Г» класса Космодемьянский Михаил Учитель: Моисеева Ирина Викторовна 2013 г.
Слайд 3В некотором царстве, в некотором государстве жил-был старый царь и было у него 3 сына.
Слайд 4Сыновья у него были умные, добрые, красивые,но вот только немного ленивые.
Слайд 5Что только не делал царь, но ни как не мог он заставить их прилежно учиться.
Слайд 6Тогда вызвал он к себе мудреца, рассказал ему о своей печали и говорит: «Посоветуй что мне делать?».
Слайд 7Мудрец задумался, а потом говорит: «Раздели своё царство так между сыновьями, чтобы они не смогли этого понять пока не изучат все науки».
Слайд 8Вот пришло время и старый царь умер. Но перед смертью он оставил им завещание, в котором написал, что старшему сыну он даёт 40/120 всего царства, среднему — 30/90, а младшему- 20/60 всего царства, а оставшуюся часть отдайте своим врагам.
Слайд 9Возмутились сначала сыновья, и заспорили: кому же большая часть досталась и сколько отдать врагу, но делать нечего, ведь своего отца они очень любили и уважали, поэтому решили исполнить его последнюю волю.
Слайд 10Сыновья поняли, чтобы узнать какую часть царства отдать врагу надо изучить свойства дробей. А для того, чтобы понять их надо уметь хорошо читать, писать и считать.
Слайд 11Несколько лет потратили сыновья на то, чтобы одолеть все науки и изучить свойства дробей. Но когда они научились складывать, вычитать и ср авнивать дроби, то поняли, какой ж е мудрый б ыл их царь-отец.
Слайд 12Оказалось, что если сократить дроби 40/120, 30/90 и 20/60, то получатся равные дроби, а значит каждому царь оставил равные части от всего царства. 40/120=30/90=20/60=1/3 А если сложить эти части, то получится 1, а это означает, что врагу ничего отдавать не надо. 1/3+1/3+1/3=1
Слайд 13Так мудрый царь-отец не только не поссорил сыновей, но и нашёл способ заставить их учиться.
Слайд 1
Муниципальное бюджетное общеобразовательное учреждение
лицей № 3
г. Воронеж
Презентация на тему:
«Математическая сказка про дроби»
Выполнил:
ученик 6 «Г» класса
Космодемьянский Михаил
Учитель:
Моисеева Ирина Викторовна
2013 г.
Слайд 2
Слайд 3
В некотором царстве, в некотором государстве жил-был старый царь и
было у него 3 сына.
Слайд 4
Сыновья у него были умные, добрые, красивые,но
вот только немного
ленивые.
Слайд 5
Что только не делал царь, но ни как не
мог он заставить их прилежно учиться.
Слайд 6
Тогда вызвал он к себе мудреца, рассказал ему о
своей печали и говорит: «Посоветуй что мне делать?».
Слайд 7
Мудрец задумался, а потом говорит: «Раздели своё царство так
между сыновьями, чтобы они не смогли этого понять пока не изучат все науки».
Слайд 8
Вот пришло время и старый царь умер. Но перед
смертью он оставил им завещание, в котором написал, что старшему сыну он даёт 40/120 всего царства, среднему — 30/90, а младшему- 20/60 всего царства, а оставшуюся часть отдайте своим врагам.
Слайд 9
Возмутились сначала сыновья, и заспорили: кому же большая часть
досталась и сколько отдать врагу, но делать нечего, ведь своего отца они очень любили и уважали, поэтому решили исполнить его последнюю волю.
Слайд 10
Сыновья поняли, чтобы узнать какую часть царства отдать врагу
надо изучить свойства дробей. А для того, чтобы понять их надо уметь хорошо читать, писать и считать.
Слайд 11
Несколько лет потратили сыновья на то, чтобы одолеть все
науки и изучить свойства дробей. Но когда они
научились
складывать,
вычитать и
сравнивать
дроби, то
поняли, какой
же мудрый
был их
царь-отец.
Слайд 12
Оказалось, что если сократить дроби 40/120, 30/90 и 20/60,
то получатся равные дроби, а значит каждому царь оставил равные части от всего царства.
40/120=30/90=20/60=1/3
А если сложить эти части, то получится 1, а это означает, что врагу ничего отдавать не надо.
1/3+1/3+1/3=1
Слайд 13
Так мудрый царь-отец не только не поссорил сыновей, но
и нашёл способ заставить их учиться.
Слайд 14
Хорошо учит, хорошо помогает детям
в учении не тот, кто знает науку, а тот, кто
умеет строить мост от незнания к знанию,
кто видит и противоположный тёмный берег
незнания и непонимания.
Симон Соловейчик
Учебный материал по математике для 5-6 классов
содержит очень много важных и сложных тем. Это и
«Обыкновенные дроби и действия с ними», и
«Десятичные дроби», и «Координатная прямая»,
«Положительные и отрицательные числа». В
определённой мере понятия абстрактные и
отличаются от количественных величин, изучаемых
в начальной школе. Чтобы повысить эффективность
усвоения данного материала, применяю в своей
практике выполнение домашнего задания в виде
творческих работ. Это написание сказок,
составление кроссвордов, собирание пословиц по
заданной теме. Ведь, чтобы написать сказку,
необходимо увидеть в новом понятии или способе
«изюминку», то чем оно отличается от других.
Уяснить каковы его особенности, в чем его суть, а
также обратить внимание на внешние признаки и
характеристики. Иначе сказка не получится.
В своём материале хочу представить содержание
некоторых детских работ моих учеников, которые
учатся сегодня, и которые уже закончили школу.
Сказка про десятичную дробь
Жило когда-то в «Математии» смешанное число,
знаменатель которого был выражен единицей и
нулями. Жило оно, не тужило, как вдруг в
«Математию» прилетел огромный дракон. Он забирал
себе то, что нравилось. И понравилось дракону у
этого смешанного числа дробная черта и «круглый»
знаменатель. Забрал всё это дракон и улетел.
Заплакало смешанное число и отправилось к
доброму математическому волшебнику. Волшебник
сказал: «Не горюй, смешанное число. Взамен
дробной черты дам я тебе компактную «запятую». И
после этого все будут называть тебя десятичной
дробью. И живёт теперь, не горюет эта
десятичная дробь.
Садыкова Регина, ученица 5А класса
Сочинение «Пропажа»
Однажды пошли слухи, что у десятичной дроби
украли запятую, а она сама сидит в пещере и
плачет. Но когда случается где-нибудь беда, там
сразу появляется Скуби-ду-би-ду, и всегда всех
выручает.
И вот однажды он пошел в эту пещеру, где сидела
десятичная дробь. Десятичная дробь ему всё
рассказала. Оказывается запятую украл её лучший
друг – Шегги и теперь ей стыдно выходить из
пещеры потому, что она стала обыкновенным числом.
И тогда Скуби пошёл искать её друга Шегги. И вот,
наконец, нашел его и увидел, где спрятана запятая.
Она висела у него на шее. Тогда Скуби стал думать,
как её спасти. И когда Шегги лёг спать, он
пробрался и снял с шеи запятую, отнёс в пещеру и
отдал десятичной дроби. И всё встало на свои
места. Но Шегги проснувшись, не обнаружил на шее
запятой, побежал скорее в пещеру, но там поджидал
его сюрприз… Десятичная дробь позвала своих
друзей и они наказали Шегги за воровство. Но как
они его наказали для нас останется загадкой.
Андреева Анжелика, ученица 5Б класса
Сказка про параллельные прямые
Жили-были параллельные прямые a и b. Однажды они
пошли в лес за ёлкой. Долго выбирали и наконец
нашли. Хотели срубить, но оказалось, что не могут.
Потому что они не пересекаются, а всегда идут
прямо параллельно друг другу.
Федякова Елена, ученица 7Б класса
Миф: «Как возникли положительные и
отрицательные числа»
Жили-были в математическом поселке АРАБЕЛЛА
два числа-друга. Одного звали АЛЬ-ДЖЕБР, а другого
АЛЬ-МУКАБАЛА. АЛЬ-ДЖЕБР – это число было очень
порядочное и воспитанное, никогда не грубило
другим числам, всегда слушалось своих родителей
и ни разу в своей жизни не обмануло взрослого
человека. А другое число, АЛЬ-МУКАБАЛА, было
хулиганом и грубияном. Оно постоянно ввязывалось
в драки, донимало всех подряд, начиная от
маленьких и заканчивая большими, никогда не
прислушивалось к советам других. За их поступки
их начали называть так: АЛЬ-ДЖЕБР –
положительным числом, а АЛЬ-МУКАБАЛА –
отрицательным числом. И до наших дней дошёл этот
миф. Учёные-математики придумали положительные и
отрицательные числа в математической науке.
Емельянова Анастасия, 5А класс
Сказка о координатной прямой
В одном графстве, которое называлось
«Координатной прямой», жили числа. В центре
города стоял главный дворец, в котором жил граф
Нуль. Он решал важные вопросы.
Население, которое проживало в этом графстве,
называли числами. У каждого числа был домик, но не
было адреса. И поэтому, когда числа ходили в гости
друг к другу, то долго блуждали, ища нужный домик.
Тогда жители начали жаловаться графу Нулю. Граф
долго думал, как решить эту проблему. И, наконец,
решил, что нужно написать адреса. Например, числа,
которые живут справа, будут иметь адрес со знаком
плюс (+1, + 2,…), а те, которые слева – со знаком
минус (–1, – 2,…).
С этого дня весь город жил тихо и никто не
жаловался на жизнь.
Пинтилина Наталья, 6А класс
Сказка о координатной прямой
Жил на свете Плюсик и не было у него никогда
друзей. Однажды Плюсик пошёл по белу свету друзей
искать. Шёл Плюсик по лесу и видит, стоит Прямая
под деревом и плачет. «Что же ты плачешь?» –
спрашивает Плюсик. «Как же мне не плакать», –
отвечает ему Прямая, — Не было у меня никогда
друзей, скучно мне одной». «А я хожу по белу свету
и ищу друзей. Пойдём со мною» – сказал Плюсик.
Прямая очень обрадовалась и предложила: «Садись
на меня я тебя прокачу. Здесь неподалёку город,
пойдём туда». Плюсик согласился, и они
отправились в путь. Долго они шли по лесу и
заблудились. «Что же теперь делать, куда идти?», –
сказал Плюсик. «Я вижу огонёк, пойдём туда», –
предложила Прямая. Когда они подошли, то увидели,
что на поляне стоял домик. Оказалось, что там жил
Минус. Он был тоже одинокий, поэтому ребята взяли
его с собой. Через некоторое время перед ними
стоял город «Чиселко», в котором жили числа.
Числа увидели Прямую, Плюсик и Минус и решили, что
это враги. Но вскоре они поняли, что трое друзей
пришли не воевать. Все они вскоре сдружились, и
прямая предложила числам идти с ними. Числа
согласились и стали рассаживаться на прямой.
Каждый хотел сесть между Плюсиком и Минусом, и
числа начали ссориться. «Я позову короля, он
лучше, знает кому где сесть», – сказала троечка.
Вскоре пришёл король Нуль. «Между Плюсиком и
Минусом сяду я», – сказал король. Все жители
замолчали и больше не ссорились. Король приказал,
чтобы всех жителей рассадили на одинаковое
расстояние друг от друга, а около короля сели
Единицы – слуги его. За ними сели Двойки, потом
Тройки, и так по очереди: 4, 5, 6. Получилось очень
интересно: с правой стороны числа со знаком «+», а
с левой со знаком «–». Королю это очень
понравилось и он издал новый указ: «Отныне числа
со знаком «+» будут положительными, а со знаком
«–» – отрицательными. А ты, Прямая, со всеми
числами будешь координатной». Так получилась
координатная прямая.
Кокшарова Елизавета, 6А класс
Тема «Прямая и обратная
пропорциональная зависимость» вызывает
затруднение у шестиклассников при определении
вида зависимости. Творческое задание по данной
теме предполагает поиск пословиц, отражающих вид
зависимости. Предварительно оговариваем, что
пропорциональность в пословицах «удержать»
затруднительно.
Пословицы, отражающие прямую
зависимость:
- Чем дальше в лес, тем больше дров.
- Как аукнется, так и откликнется.
- Много снега, много хлеба.
- Кто рано встаёт, тому Бог подаёт.
- Как потопаешь, так и полопаешь.
- Выучишь правило, выполнишь верно задание.
- Кто много читает, тот много знает.
Пословицы, отражающие обратную
зависимость:
- Тише едешь, дальше будешь.
- Мир строит, а война разрушает.
- Меньше народа, больше кислорода.
- Лето собирает, зима съедает.
- Было густо, стало пусто.
- Мал грех, да большую вину несёт.
- С большого грома – малый дождь.
- Меньше слов – больше дела.
Творческие работы учащихся
Аппликация из геометрических фигур.
Автор: Голубева Алёна, 5Б класс.
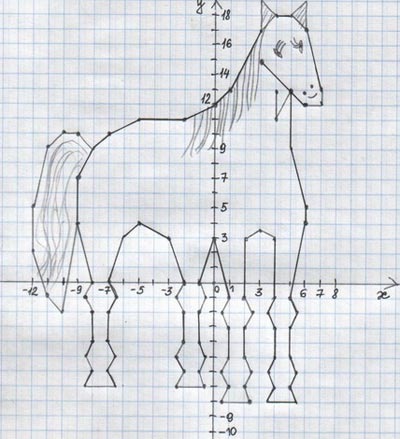
Рисуем в координатной плоскости.
Автор: Елисеева Анна, 6А класс.
Выполнение творческих работ позволяет
повысить интерес к изучаемым темам даже у слабых
учащихся. Как правило, задания подобного типа не
вызывают у них трудностей, повышают интерес к
математике и помогают сделать «нелюбимый»
предмет доступным. Сильные же ученики, благодаря
творческим работам, овладевают способностью
переводить сложный математический материал в
мир фантазий и красок. Данные задания позволяют
показать красоту науки математики, её
взаимосвязь с общечеловеческой культурой.
Улучшают эмоциональное состояние учащихся.
Повышают их интеллектуальное развитие и ведут к
формированию всесторонне развитой личности.