В предыдущей статье мы рассказывали, как правильно вычислять пределы элементарных функций. Если же мы возьмем более сложные функции, то у нас в расчетах появятся выражения с неопределенным значением. Они и называются неопределенностями.
Выделяют следующие основные виды неопределенностей:
- Деление 0 на 0 00;
- Деление одной бесконечности на другую ∞∞;
-
0, возведенный в нулевую степень 00;
- бесконечность, возведенная в нулевую степень ∞0.
Мы перечислили все основные неопределенности. Другие выражения в различных условиях могут принимать конечные или бесконечные значения, следовательно, они не могут считаться неопределенностями.
Раскрытие неопределенностей
Раскрыть неопределенность можно:
- С помощью упрощения вида функции (использование формул сокращенного умножения, тригонометрических формул, дополнительное умножение на сопряженные выражения и последующее сокращение и др. );
-
С помощью замечательных пределов;
-
С помощью правила Лопиталя;
-
Заменив одно бесконечно малое выражение на эквивалентное ему выражение (как правило, это действие выполняется с помощью таблицы бесконечно малых выражений).
Всю информацию, представленную выше, можно наглядно представить в виде таблицы. С левой стороны в ней приводится вид неопределенности, с правой – подходящий метод ее раскрытия (нахождения предела). Этой таблицей очень удобно пользоваться при расчетах, связанных с нахождением пределов.
| Неопределенность | Метод раскрытия неопределенности |
| 1. Деление 0 на 0 | Преобразование и последующее упрощение выражения. Если выражение имеет вид sin(kx)kx или kxsin(kx) то нужно использовать первый замечательный предел. Если такое решение не подходит, пользуемся правилом Лопиталя или таблицей эквивалентных бесконечно малых выражений |
| 2. Деление бесконечности на бесконечность | Преобразование и упрощение выражения либо использование правила Лопиталя |
| 3. Умножение нуля на бесконечность или нахождение разности между двумя бесконечностями | Преобразование в 00 или ∞∞ с последующим применением правила Лопиталя |
| 4. Единица в степени бесконечности | Использование второго замечательного предела |
| 5. Возведение нуля или бесконечности в нулевую степень | Логарифмирование выражения с применением равенства limx→x0ln(f(x))=lnlimx→x0f(x) |
Разберем пару задач. Эти примеры довольно простые: в них ответ получается сразу после подстановки значений и неопределенности при этом не возникает.
Вычислите предел limx→1×3+3x-1×5+3.
Решение
Выполняем подстановку значений и получаем ответ.
limx→1×3+3x-1×5+3=13+3·1-115+3=34=32
Ответ: limx→1×3+3x-1×5+3=32.
Вычислите предел limx→0(x2+2,5)1×2.
Решение
У нас есть показательно степенная функция, в основание которой нужно подставитьx=0.
(x2+2,5)x=0=02+2,5=2,5
Значит, мы можем преобразовать предел в следующее выражение:
limx→0(x2+2,5)1×2=limx→02,51×2
Теперь разберемся с показателем – степенной функцией 1×2=x-2. Заглянем в таблицу пределов для степенных функций с показателем меньше нуля и получим следующее: limx→0+01×2=limx→0+0x-2=+∞ и limx→0+01×2=limx→0+0x-2=+∞
Таким образом, можно записать, что limx→0(x2+2,5)1×2=limx→02,51×2=2,5+∞.
Теперь берем таблицу пределов показательных функций с основаниями, большими 0, и получаем:
limx→0(x2+2,5)1×2=limx→02,51×2=2,5+∞=+∞
Ответ: limx→0(x2+2,5)1×2=+∞.
Далее мы приведем примеры решений задач на раскрытие неопределенностей с использованием метода преобразования. На практике выполнять это приходится довольно часто.
Вычислите предел limx→1×2-1x-1.
Решение
Выполняем подстановку значений.
limx→1×2-1x-1=12-11-1=00
В итоге у нас получилась неопределенность. Используем таблицу выше, чтобы выбрать метод решения. Там указано, что нужно выполнить упрощение выражения.
limx→1×2-1x-1=00=limx→1(x-1)·(x+1)x-1==limx→1(x-1)·(x+1)·(x+1)x-1=limx→1(x+1)·x-1==1+1·1-1=2·0=0
Как мы видим, упрощение привело к раскрытию неопределенности.
Ответ: limx→1×2-1x-1=0
Вычислите предел limx→3x-312-x-6+x.
Решение
Подставляем значение и получаем запись следующего вида.
limx→3x-312-x-6+x=3-312-3-6+3=09-9=00
Мы пришли к необходимости делить нуль на нуль, что является неопределенностью. Посмотрим нужный метод решения в таблице – это упрощение и преобразование выражения. Выполним дополнительное умножение числителя и знаменателя на сопряженное знаменателю выражение 12-x+6+x:
limx→3x-312-x-6+x=00=limx→3x-312-x+6+x12-x-6+x12-x+6+x
Домножение знаменателя выполняется для того, чтобы потом можно было воспользоваться формулой сокращенного умножения (разность квадратов) и выполнить сокращение.
limx→3x-312-x+6+x12-x-6+x12-x+6+x=limx→3x-312-x+6+x12-x2-6+x2=limx→3(x-3)12-x+6+x12-x-(6+x)==limx→3(x-3)12-x+6+x6-2x=limx→3(x-3)12-x+6+x-2(x-3)==limx→312-x+6+x-2=12-3+6+3-2=9+9-2=-9=-3
Как мы видим, в результате этих действий нам удалось избавиться от неопределенности.
Ответ: limx→3x-312-x-6+x=-3.
Важно отметить, что при решении подобных задач подход с использованием домножения используется очень часто, так что советуем запомнить, как именно это делается.
Вычислите предел limx→1×2+2x-33×2-5x+2.
Решение
Выполняем подстановку.
limx→1×2+2x-33×2-5x+2=12+2·1-33·12-5·1+2=00
В итоге у нас вышла неопределенность. Рекомендуемый способ решения задачи в таком случае – упрощение выражения. Поскольку при значении x, равном единице, числитель и знаменатель обращаются в 0, то мы можем разложить их на множители и потом сократить на х-1,и тогда неопределенность исчезнет.
Выполняем разложение числителя на множители:
x2+2x-3=0D=22-4·1·(-3)=16⇒x1=-2-162=-3×2=-2+162=1⇒x2+2x-3=x+3x-1
Теперь делаем то же самое со знаменателем:
3×2-5x+2=0D=-52-4·3·2=1⇒x1=5-12·3=23×2=5+12·3=1⇒3×2-5x+3=3x-23x-1
Мы получили предел следующего вида:
limx→1×2+2x-33×2-5x+2=00=limx→1x+3·x-13·x-23·x-1==limx→1x+33·x-23=1+33·1-23=4
Как мы видим, в ходе преобразования нам удалось избавиться от неопределенности.
Ответ: limx→1×2+2x-33×2-5x+2=4.
Далее нам нужно рассмотреть случаи пределов на бесконечности от степенных выражений. Если показатели этих выражений будут больше 0, то предел на бесконечности также окажется бесконечным. При этом основное значение имеет самая большая степень, а остальные можно не учитывать.
Например, limx→∞(x4+2×3-6)=limx→∞x4=∞ или limx→∞x4+4×3+21×2-115=limx→∞x45=∞.
Если под знаком предела у нас стоит дробь со степенными выражениями в числителе и знаменателе, то при x→∞ у нас возникает неопределенность вида ∞∞. Чтобы избавиться от этой неопределенности, нам нужно разделить числитель и знаменатель дроби на xmax(m,n). Приведем пример решения подобной задачи.
Вычислите предел limx→∞x7+2×5-43×7+12.
Решение
limx→∞x7+2×5-43×7+12=∞∞
Степени числителя и знаменателя равны 7. Делим их на x7 и получаем:
limx→∞x7+2×5-43×7+12=limx→∞x7+2×5-4x73x7+12×7==limx→∞1+2×2-4×73+12×7=1+2∞2-4∞73+12∞7=1+0-03+0=13
Ответ: limx→∞x7+2×5-43×7+12=13.
Вычислите предел limx→∞x8+113×2+x+1.
Решение
limx→∞x8+113×2+x+1=∞∞
Числитель имеет степень 83, а знаменатель 2. Выполним деление числителя и знаменателя на x83:
limx→∞x8+113×2+x+1=∞∞=limx→∞x8+113x83x2+x+1×83==limx→∞1+11x831x23+1×53+1×83=1+11∞31∞+1∞+1∞=1+030+0+0=10=∞
Ответ: limx→∞x8+113×2+x+1=∞.
Вычислите предел limx→∞x3+2×2-1×10+56×7+123.
Решение
limx→∞x3+2×2-1×10+56×7+123=∞∞
У нас есть числитель в степени 3 и знаменатель в степени 103. Значит, нам нужно разделить числитель и знаменатель на x103:
limx→∞x3+2×2-1×10+56×7+123=∞∞=limx→∞x3+2×2-1x103x10+56×7+123×103==limx→∞1×13+2×43-1×1031+56×3+12×103=1∞+2∞-1∞1+56∞+12∞3=0+0-01+0+03=0
Ответ: limx→∞x3+2×2-1×10+56×7+123=0.
Выводы
В случае с пределом отношений возможны три основных варианта:
-
Если степень числителя равна степени знаменателя, то предел будет равен отношению коэффициентов при старших степенях.
-
Если степень числителя будет больше степени знаменателя, то предел будет равен бесконечности.
-
Если степень числителя меньше степени знаменателя, то предел будет равен нулю.
Другие методы раскрытия неопределенностей мы разберем в отдельных статьях.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim — от английского limit — предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача — найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент: предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Очень часто при вычислении пределов функций в какой-либо точке в результате упрощения получаются выражения, не несущие какой-либо информации об этой функции. Такие выражения носят название неопределённостей.
Виды неопредлённостей
-
$frac{0}{0}$ — деление нуля на нуль;
-
$frac{infty}{infty}$ — деление бесконечности на бесконечность;
-
$0 cdot infty$ — умножение нуля на бесконечность;
-
$1^{infty}$ — единица, возведённая в степень бесконечности;
-
$(infty-infty$) — разность бесконечностей;
-
$0^0$ — нуль в нулевой степени;
-
$infty^0$ — бесконечность в степени 0.
Неопределённости вида $frac{0}{0}$ и $frac{infty}{infty}$ называются основными и для их раскрытия применяется правило Лопиталя, тогда как остальные неопределённости сводятся путём тождественных преобразований также к основным или решаются иными способами.
Раскрытие неопределенностей
Сам по себе термин «неопределённость» не означает, что предела не существует. Во многих случаях для того чтобы прийти к конечному ответу можно использовать упрощения, правило Лопиталя и другие способы раскрытия математических неопределенностей.
Например, выражение вида $frac{x^2}{x}$ можно упростить до просто $x$ при любых значениях $x$, кроме нуля. Таким образом, предел этого выражения при приближении $x$ к нулю есть не что иное как $x$, а сам $x$ стремится к нулю, следовательно:
$lim_{xto 0}frac{x^2}{x}=lim_{xto 0} x=0$.
Наиболее универсальным способом для раскрытия неопределённостей является правило Лопиталя, но к нему не всегда возможно прибегнуть. Как было упомянуто выше, его возможно применять лишь к двум видам неопределённостей, тогда как остальные необходимо для начала привести к одной из форм основных неопределённостей.
В целом, при раскрытии неопредлённостей возможно использовать различные тождественные преобразования, замечательные пределы и замену одного бесконечно малого выражения на другое, подобное ему.
«Неопределенности пределов» 👇
Рассмотрим подробнее замену бесконечно малых выражений на аналогичное.
Таблица эквивалентных бесконечно малых выражений
Если две переменные $α$ и $β$ сходятся к нулю в одной точке и предел их отношения в этой точке равен единице, то эти переменные называются эквивалентными бесконечно малыми переменными.
Таблица эквивалентных бесконечно малых функций:
$x~sin x$;
$x~arcsin x$;
$x ~ tg x$;
$x ~ arctg x$;
$x ~ ln(1+x)$;
$1-cos x ~ frac{x^2}{2}$;
$ a^x-1 ~ x ln a$;
$e^x-1 ~ x$;
$(1+x)^a-1 ~ ax$.
Пример 1
Вычислите предел: $lim_{x to 0}frac{1}{x^3} cdot (frac{2+cosx}{3})^x-1)$.
Решение:
$lim_{x to 0}frac{1}{x^3} cdot (frac{2+cosx}{3})^x-1)=lim_{x to 0}frac{e^{xln frac{2+cosx}{3}}-1}{x^3}= lim_{x to 0}frac{1}{x^2} ln frac{2+cosx}{3}= lim_{x to 0}frac{1}{x^2} ln (frac{cosx-1}{3}+1=lim_{x to 0}frac{cosx-1}{3x^2}=-frac{1}{6}$
Раскрытие неопределённости, содержащей бесконечность в числителе и знаменателе
Для того чтобы раскрыть такую неопределённость, сначала находят в выражении старшую степень при переменной, а затем делят на эту переменную числитель и знаменатель.
Раскрытие неопределённости, содержащей нуль в числителе и знаменателе
При возникновении такого случая сначала производят разложение на множители числителя и знаменателя, а затем осуществляют сокращение дроби.
Правило Лопиталя для раскрытия неопределённостей
Данное правило является главным методом для вычисления неопределённостей вида $frac{0}{0}$ и $frac{infty}{infty}$. Суть метода состоит в том, чтобы вместо предела отношения двух функций находить предел производных двух функций:
$lim_{xto c} frac{f(x)}{g(x)}=lim_{xto c} frac{f’(x)}{g’(x)}$
Использование производных позволяет упростить выражения и найти, к чему стремится данный предел.
С помощью этого правила можно находить не только неопределённости, про которые сказано выше, но также и другие. Ниже приведена таблица, с помощью которой можно непределённости других видов приводить к форме, которую возможно упростить с помощью правила Лопиталя.
Рисунок 1. Преобразования неопределенностей пределов для применения правила Лопиталя
Пример 2
Вычислите предел, используя правило Лопиталя:
$lim_{x to 0} frac{x^2+5x}{3x}$
Решение:
$lim_{x to 0} frac{x^2+5x}{3x}= lim_{x to 0} frac{(x^2+5x)’}{(3x)’}=lim_{x to 0}frac{2x+5}{3}=frac{5}{3}$
Разложение неопределённостей в ряд Тейлора
Для оценки выражений, в результате вычисления которых образовались неопределённости вида $0^0$, $1^{infty}$, и $infty^0$ вычисляют предел натурального логарифма исследуемого выражения, а затем после получения результата от него берут экспоненту:
$0^0=e^{0 cdot (- infty)}$
$1^{infty}= e^{infty cdot ln1}= e^{infty cdot 0}$
$infty^0=e^{0 ln infty}= e^ { 0 cdot infty}$
Выражения, не являющиеся неопределённостями
Выражения вида $frac{1}{0}$ не считаются неопределённостями, также как неопределённости не рассматриваются все случаи, где знаменатель равен нулю, а числитель — любое число, отличное от нуля.
Другое выражение, не являющееся неопределённостью — это $0^{infty}$. Выражение вида $0^{+infty}$ стремится к нулю, тогда как выражение $0^{-infty}$ эквивалентно выражению $frac{1}{0}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Неопределённость (математика)
- Неопределённость (математика)
-
Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа
,
, 0 / 0, 00,
,
,
по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.
Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.
Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.
Для раскрытия неопределённостей видов 00,
,
пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.
Пример
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое «Неопределённость (математика)» в других словарях:
-
Математика — I. Определение предмета математики, связь с другими науками и техникой. Математика (греч. mathematike, от máthema знание, наука), наука о количественных отношениях и пространственных формах действительного мира. «Чистая … Большая советская энциклопедия
-
Регрессия (математика) — У этого термина существуют и другие значения, см. регрессия. Регрессия (лат. regressio обратное движение, отход), в теории вероятностей и математической статистике, зависимость среднего значения какой либо величины от некоторой другой… … Википедия
-
ИНТУИЦИЯ — (от позднелат. intuitio, от лат. intueor пристальное, внимательное всматривание, созерцание) способность к прямому усмотрению истины, постижению ее без всякого рассуждения и доказательства. Для И. обычно считаются типичными неожиданность,… … Философская энциклопедия
-
ФИЗИКА. — ФИЗИКА. 1. Предмет и структура физики Ф. наука, изучающая простейшие и вместе с тем наиб. общие свойства и законы движения окружающих нас объектов материального мира. Вследствие этой общности не существует явлений природы, не имеющих физ. свойств … Физическая энциклопедия
-
Маймон, Соломон — В Википедии есть статьи о других людях с такой фамилией, см. Маймон. Соломон Маймон Salomon Maimon нем. Arndt, портрет Соломона Маймона Имя при рождении: Шлойме Хайман … Википедия
-
Шрёдингер, Эрвин — Эрвин Шрёдингер Erwin Schrödinger Эрвин Шрёдингер в 1933 году Дата рожден … Википедия
-
Информация — (Information) Информация это сведения о чем либо Понятие и виды информации, передача и обработка, поиск и хранение информации Содержание >>>>>>>>>>>> … Энциклопедия инвестора
-
КОДИРОВАНИЕ ИНФОРМАЦИИ — установление соответствия между элементами сообщения и сигналами, при помощи к рых эти элементы могут быть зафиксированы. Пусть В, , множество элементов сообщения, А алфавит с символами , Пусть конечная последовательность символов наз. словом в… … Физическая энциклопедия
-
Гамильтониан — Эта статья об операторе Гамильтона в квантовой механике. О функции Гамильтона в классической механике см. Функция Гамильтона. … Википедия
-
Гамильтониан (квантовая механика) — Эта статья об операторе Гамильтона в квантовой механике. О функции Гамильтона в классической механике см. Функция Гамильтона. … Википедия
In mathematics, the term undefined is often used to refer to an expression which is not assigned an interpretation or a value (such as an indeterminate form, which has the propensity of assuming different values).[1] The term can take on several different meanings depending on the context. For example:
Undefined terms[edit]
In ancient times, geometers attempted to define every term. For example, Euclid defined a point as «that which has no part». In modern times, mathematicians recognize that attempting to define every word inevitably leads to circular definitions, and therefore leave some terms (such as «point») undefined (see primitive notion for more).
This more abstract approach allows for fruitful generalizations. In topology, a topological space may be defined as a set of points endowed with certain properties, but in the general setting, the nature of these «points» is left entirely undefined. Likewise, in category theory, a category consists of «objects» and «arrows», which are again primitive, undefined terms. This allows such abstract mathematical theories to be applied to very diverse concrete situations.
In arithmetic[edit]
The expression 0/0 is undefined in arithmetic, as explained in division by zero (the same expression is used in calculus to represent an indeterminate form).
Mathematicians have different opinions as to whether 00 should be defined to equal 1, or be left undefined.
Values for which functions are undefined[edit]
The set of numbers for which a function is defined is called the domain of the function. If a number is not in the domain of a function, the function is said to be «undefined» for that number. Two common examples are 



In trigonometry[edit]
In trigonometry, for all 






In complex analysis[edit]
In complex analysis, a point 



In computer science[edit]
Notation using ↓ and ↑[edit]
In computability theory, if 




If 



The symbols of infinity[edit]
In analysis, measure theory and other mathematical disciplines, the symbol 


Performing standard arithmetic operations with the symbols 
No sensible extension of addition and multiplication with 
For more detail, see extended real number line.
References[edit]
- ^ Weisstein, Eric W. «Undefined». mathworld.wolfram.com. Retrieved 2019-12-15.
- ^ «Undefined vs Indeterminate in Mathematics». www.cut-the-knot.org. Retrieved 2019-12-15.
- ^ Enderton, Herbert B. (2011). Computability: An Introduction to Recursion Theory. Elseveier. pp. 3–6. ISBN 978-0-12-384958-8.
Further reading[edit]
- Smart, James R. (1988). Modern Geometries (Third ed.). Brooks/Cole. ISBN 0-534-08310-2.
In mathematics, the term undefined is often used to refer to an expression which is not assigned an interpretation or a value (such as an indeterminate form, which has the propensity of assuming different values).[1] The term can take on several different meanings depending on the context. For example:
Undefined terms[edit]
In ancient times, geometers attempted to define every term. For example, Euclid defined a point as «that which has no part». In modern times, mathematicians recognize that attempting to define every word inevitably leads to circular definitions, and therefore leave some terms (such as «point») undefined (see primitive notion for more).
This more abstract approach allows for fruitful generalizations. In topology, a topological space may be defined as a set of points endowed with certain properties, but in the general setting, the nature of these «points» is left entirely undefined. Likewise, in category theory, a category consists of «objects» and «arrows», which are again primitive, undefined terms. This allows such abstract mathematical theories to be applied to very diverse concrete situations.
In arithmetic[edit]
The expression 0/0 is undefined in arithmetic, as explained in division by zero (the same expression is used in calculus to represent an indeterminate form).
Mathematicians have different opinions as to whether 00 should be defined to equal 1, or be left undefined.
Values for which functions are undefined[edit]
The set of numbers for which a function is defined is called the domain of the function. If a number is not in the domain of a function, the function is said to be «undefined» for that number. Two common examples are 



In trigonometry[edit]
In trigonometry, for all 






In complex analysis[edit]
In complex analysis, a point 



In computer science[edit]
Notation using ↓ and ↑[edit]
In computability theory, if 




If 



The symbols of infinity[edit]
In analysis, measure theory and other mathematical disciplines, the symbol 


Performing standard arithmetic operations with the symbols 
No sensible extension of addition and multiplication with 
For more detail, see extended real number line.
References[edit]
- ^ Weisstein, Eric W. «Undefined». mathworld.wolfram.com. Retrieved 2019-12-15.
- ^ «Undefined vs Indeterminate in Mathematics». www.cut-the-knot.org. Retrieved 2019-12-15.
- ^ Enderton, Herbert B. (2011). Computability: An Introduction to Recursion Theory. Elseveier. pp. 3–6. ISBN 978-0-12-384958-8.
Further reading[edit]
- Smart, James R. (1988). Modern Geometries (Third ed.). Brooks/Cole. ISBN 0-534-08310-2.
Содержание:
- Раскрытие неопределенностей
- Основные пределы
- Основные виды неопределенностей:
$leftlceilfrac{0}{0}rightrceil$
, $left[frac{infty}{infty}right]$
, $[0 cdot infty]$
, $[infty-infty]$
, $left[1^{infty}right]$
, $left[0^{0}right]$
, $left[infty^{0}right]$
Определение
При вычислении пределов зачастую появляются выражения, значение которых не определено.
Такие выражения называют неопределенностями.
Основные виды неопределенностей:
$leftlceilfrac{0}{0}rightrceil$
, $left[frac{infty}{infty}right]$
, $[0 cdot infty]$
, $[infty-infty]$
, $left[1^{infty}right]$
, $left[0^{0}right]$
, $left[infty^{0}right]$
Все другие выражения не являются неопределенностями и принимают какое-то конкретное конечное или бесконечное значение.
Раскрытие неопределенностей
Для раскрытия неопределенностей используют следующее:
- упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью
формул сокращенного
умножения, тригонометрических формул,
домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.; - замечательные пределы — первый замечательный предел и
второй замечательный предел; - правило Лопиталя;
- эквивалентные бесконечно малые функции.
Основные пределы
1. Первый замечательный предел: $lim _{x rightarrow 0} frac{sin x}{x}=1$
Пример
Задание. Вычислить предел $lim _{x rightarrow 0} frac{sin 3 x}{arcsin 7 x}$
Решение. Получим неопределенность, сделаем замену. При $x rightarrow 0$:
$sin x sim x$,
$arcsin x sim x$
$lim _{x rightarrow 0} frac{sin 3 x}{arcsin 7 x}left[frac{0}{0}right]=lim _{x rightarrow 0} frac{3 x}{7 x}=lim _{x rightarrow 0} frac{3}{7}=frac{3}{7}$
Ответ. $lim _{x rightarrow 0} frac{sin 3 x}{arcsin 7 x}=frac{3}{7}$
2. Второй замечательный предел: $lim _{x rightarrow infty}left(1+frac{1}{x}right)^{x}=e$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить предел $lim _{x rightarrow infty}left(frac{x+1}{x-1}right)^{x}$
Решение. Получим неопределенность и для решения предела воспользуемся вторым замечательным пределом.
$lim _{x rightarrow infty}left(frac{x+1}{x-1}right)^{x}left[1^{infty}right]=lim _{x rightarrow infty}left(1+frac{x+1}{x-1}-1right)^{x}=$
$=lim _{x rightarrow infty}left(1+frac{x+1-x+1}{x-1}right)^{x}=lim _{x rightarrow infty}left(1+frac{2}{x-1}right)^{x}=$
$=lim _{x rightarrow infty}left[left(1+frac{2}{x-1}right)^{frac{x-1}{2}}right]^{x cdot frac{2}{x-1}}=lim _{x rightarrow infty} e^{frac{2 x}{x-1}}=$
$=e^{lim _{x rightarrow infty} frac{2 x}{x-1}left[frac{infty}{infty}right]}=e^{lim _{x rightarrow infty} frac{2 x}{xleft(1-frac{1}{x}right)}}=e^{lim _{x rightarrow infty} frac{2}{1-frac{1}{x}}}=e^{2}$
Ответ. $lim _{x rightarrow infty}left(frac{x+1}{x-1}right)^{x}=e^{2}$
3. Предел частного многочленов на бесконечности:
$lim _{x rightarrow infty} frac{a_{n} x^{n}+a_{n-1} x^{n-1}+ldots+a_{1} x+a_{0}}{b_{m} x^{m}+b_{m-1} x^{m-1}+ldots+b_{1} x+b_{0}}=left{begin{array}{l}{0, n lt m} \ {frac{a_{n}}{b_{m}}, n=m} \ {infty, n>m}end{array}right.$
Пример
Задание. Найти предел $lim _{x rightarrow infty} frac{3 x^{3}-x^{2}+14}{x^{2}-4}$
Решение. $lim _{x rightarrow infty} frac{3 x^{3}-x^{2}+14}{x^{2}-4}left[frac{infty}{infty}right]=left|begin{array}{l}
n=3 \
m=2 \
n>m
end{array}right|=infty$
Ответ. $lim _{x rightarrow infty} frac{3 x^{3}-x^{2}+14}{x^{2}-4}=infty$
4. Предел целой рациональной функции: если $P(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+ldots+a_{1} x+a_{0}$ , то
$lim _{x rightarrow a} P(x)=P(a)$
Пример
Задание. Найти предел функции $f(x)=x^{2}+1$ в точке
$x=1$
Решение. $lim _{x rightarrow 1} f(x)=f(1)=1^{2}+1=2$
5. Пределы иррациональных выражений:
а) чтобы найти предел дроби, содержащей иррациональное выражение в случае, когда предел и числителя, и знаменателя
равен нулю, надо перенести иррациональность из числителя в знаменатель, или из знаменателя в числитель и после этого
сделать необходимые упрощения. Иррациональность переносится с помощью домножения и числителя и знаменателя дроби на
выражение, сопряженное к иррациональности.
Пример
Задание. Вычислить предел $lim _{x rightarrow 2} frac{sqrt{x^{2}+5}-3}{x-2}$
Решение. Получим неопределенность и домножим числитель и знаменатель на выражение, сопряженное к иррациональности.
$lim _{x rightarrow 2} frac{sqrt{x^{2}+5}-3}{x-2}left[frac{0}{0}right]=lim _{x rightarrow 2} frac{sqrt{x^{2}+5}-3}{x-2} cdot frac{sqrt{x^{2}+5}+3}{sqrt{x^{2}+5}+3}=$
$=lim _{x rightarrow 2} frac{x^{2}+5-9}{(x-2)left(sqrt{x^{2}+5}+3right)}=lim _{x rightarrow 2} frac{x^{2}-4}{(x-2)left(sqrt{x^{2}+5}+3right)}=$
$=lim _{x rightarrow 2} frac{(x-2)(x+2)}{(x-2)left(sqrt{x^{2}+5}+3right)}=lim _{x rightarrow 2} frac{x+2}{sqrt{x^{2}+5}+3}=$
$=frac{2+2}{sqrt{4+5}+3}=frac{4}{6}=frac{2}{3}$
Ответ. $lim _{x rightarrow 2} frac{sqrt{x^{2}+5}-3}{x-2}=frac{2}{3}$
б) Вычисление пределов, содержащих разность корней:
Пример
Задание. Вычислить предел $lim _{x rightarrow infty}left(sqrt{x^{2}-7}-sqrt{x^{2}+5}right)$
Решение. Получим неопределенность и домножим и поделим выражение на сопряженное.
$lim _{x rightarrow infty}left(sqrt{x^{2}-7}-sqrt{x^{2}+5}right)[infty-infty]=$
$=lim _{x rightarrow infty} frac{left(sqrt{x^{2}-7}-sqrt{x^{2}+5}right)left(sqrt{x^{2}-7}+sqrt{x^{2}+5}right)}{left(sqrt{x^{2}-7}+sqrt{x^{2}+5}right)}=$
$=lim _{x rightarrow infty} frac{x^{2}-7-x^{2}-5}{left(sqrt{x^{2}-7}+sqrt{x^{2}+5}right)}=$
$=lim _{x rightarrow infty} frac{-12}{left(sqrt{x^{2}-7}+sqrt{x^{2}+5}right)}left[frac{-12}{infty}right]=0$
Ответ. $lim _{x rightarrow infty}left(sqrt{x^{2}-7}-sqrt{x^{2}+5}right)=0$
6. Раскрытие неопределенности $left[frac{0}{0}right]$
в частном двух многочленов с помощью разложения на множители:
Пример
Задание. Вычислить предел $lim _{x rightarrow 2} frac{x^{2}-4}{x^{2}-5 x+6}$
Решение. Получим неопределенность, разложим на множители числитель и знаменатель, сократим одинаковые элементы.
$lim _{x rightarrow 2} frac{x^{2}-4}{x^{2}-5 x+6}left[frac{0}{0}right]=lim _{x rightarrow 2} frac{(x-2)(x+2)}{(x-2)(x-3)}=$
$=lim _{x rightarrow 2} frac{x+2}{x-3}=frac{2+2}{2-3}=-4$
Ответ. $lim _{x rightarrow 2} frac{x^{2}-4}{x^{2}-5 x+6}=-4$
Читать дальше: понятие непрерывности функции в точке.
Правило. Для
вычисления предела функции
в точке
или при
надо применить теоремы о пределах и
подставить предельное значение аргумента.
Для всех основных
элементарных функций в любой точке их
области определения имеет место равенство

Примеры
Найти пределы
функций:
2.

3.

4.

5.

При вычислении
пределов функций формальная подстановка
вместо х
предельного значения
часто приводит к неопределенным
выражениям вида:,
,
,
,
,
,
.
Например,


Выражения вида
,
,
,
,
,
,
называютсянеопределенностями.
Вычисление предела
функции в этих случаях называют раскрытием
неопределенности.
Рассмотрим правила
раскрытия таких неопределенностей.
Неопределенность вида
Если
и
при
(
),
то говорят, что их частноепредставляет собой неопределенность
вида.
Правило. Чтобы
раскрыть неопределенность вида
,
заданную отношением двух многочленов,
надо и числитель и знаменатель разделить
на самую высокую входящую в них степеньх.
Например,

Рассмотрим
дробно−рациональную функцию

),
представляющую
собой отношение двух многочленов
относительно х
степеней m
и n
соответственно, и исследуем поведение
этой функции при
.
При нахождении
предела данной функции при
могут иметь место три варианта ответа:
|
1. |
|
|
2. |
|
|
3. |
|
Из этого следует,
что предел отношения двух многочленов
при
во всех случаях равен пределу отношения
их старших членов.
Примеры
Найти пределы
функций:
1.
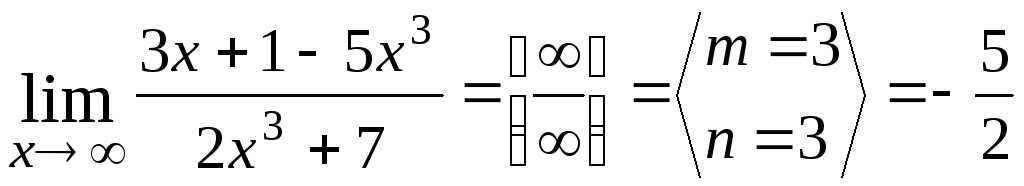
2.

3.

Неопределенность
вида
Если требуется
найти

гдеи
− бесконечно малые функции при
(
),
т.е.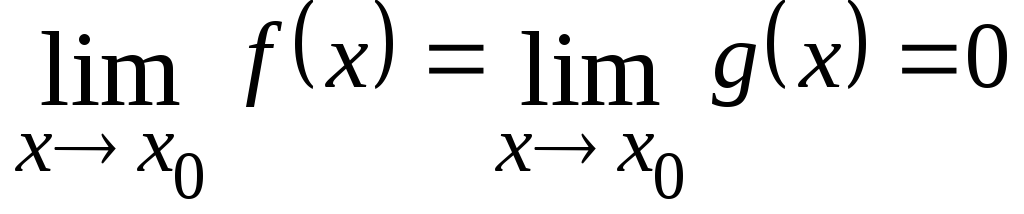
то в этом случае вычисление предела
называют раскрытием неопределенности
вида
.
Рассмотрим возможные
приемы раскрытия такой неопределенности.
Выделение критического множителя
Правило. Чтобы
раскрыть неопределенность вида
,
заданную отношением двух многочленов,
надо и в числителе и в знаменателе
выделить критический множитель и
сократить на него дробь.
Примеры
Найти пределы
функций:
1.

2.

Преобразование иррациональных
выражений
Правило. Чтобы
раскрыть неопределенность вида
,
в которой числитель или знаменатель,
или тот и другой иррациональны, надо:
− перенести
иррациональность из числителя в
знаменатель, или из знаменателя в
числитель, домножив дробь на сопряженные
выражения,
− либо сделать
замену переменной.
Замечание.
Если под знаком
предела делается замена переменной, то
все величины, входящие под знак предела,
должны быть выражены через эту новую
переменную. Из равенства, выражающего
зависимость между старой переменной и
новой, должен быть определен предел
новой переменной.
Примеры
Найти пределы
функций:
1.
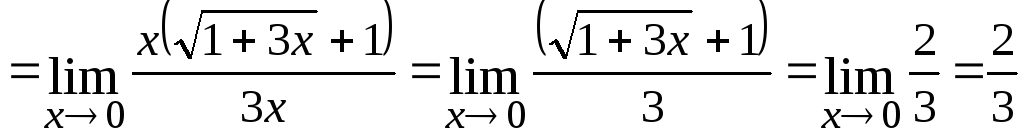
2.

3.

4.
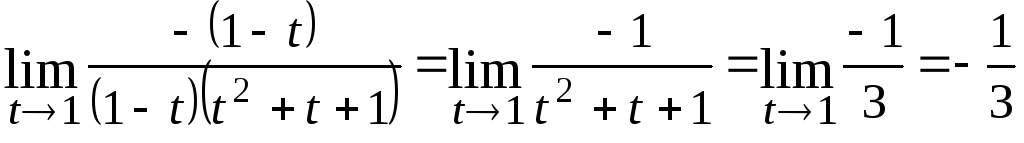
Применение первого замечательного
предела
Правило. Для
раскрытия неопределенности вида
,
содержащей тригонометрические выражения,
используют первый замечательный предел:


где
и
.
Примеры
Найти пределы
функций:
1.
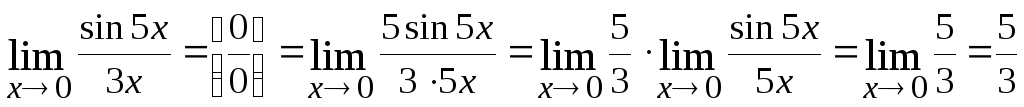
2.

4.

Применение эквивалентных бесконечно
малых величин
Правило. Для
раскрытия неопределенности вида
можно и числитель и знаменатель заменить
величинами им эквивалентными (п.2.12).
Примеры
Найти пределы
функций:
1.

2.

3.

4.
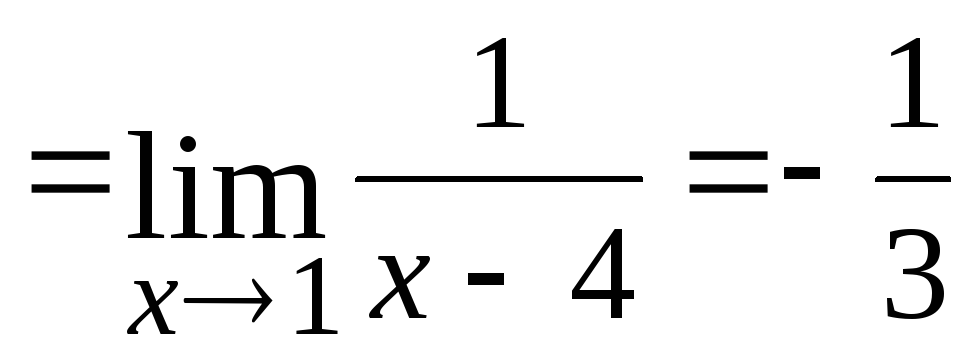
Неопределенности
вида
и
Если
и
при
,
то их разностьпредставляет собой неопределенность
вида
.
Если
и
при
,
то их произведение− это неопределенность вида
.
Правило.
Неопределенности
вида
и
раскрываются путем их преобразования
и сведения к неопределенностям видаили
.
Примеры
Найти пределы
функций:
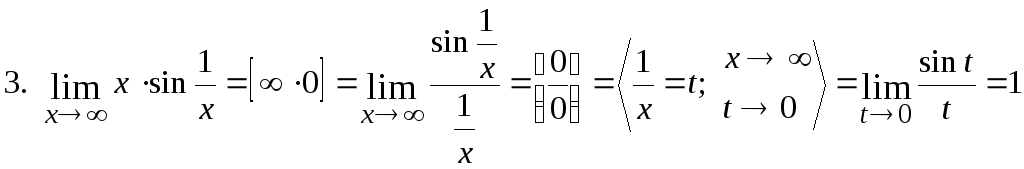
Неопределенности
вида
,
,
Пусть функция
имеет вид:
.
Если при
,
,
а,
то имеем неопределенность вида
.
Для раскрытия этой неопределенности
применяют второй замечательный предел:


или
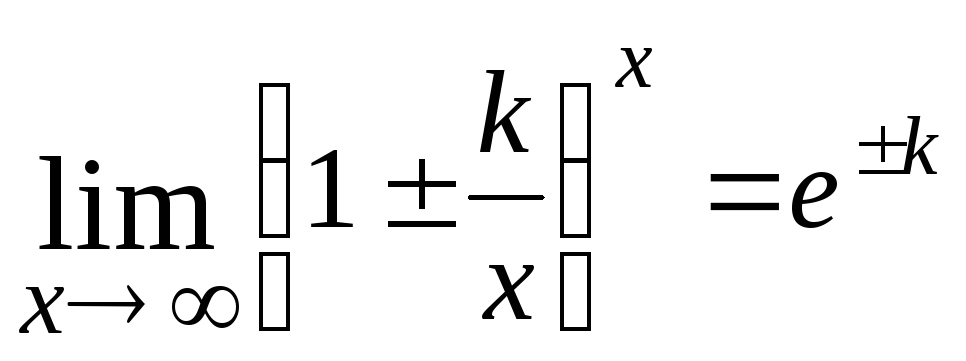
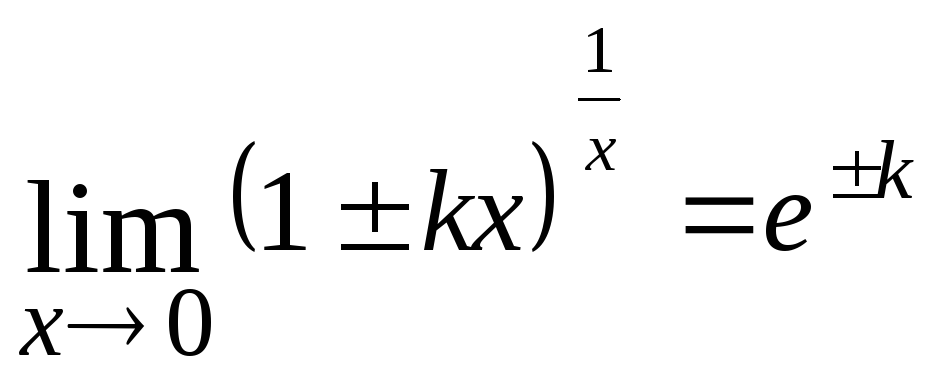
Примеры
Найти пределы
функций:
1.
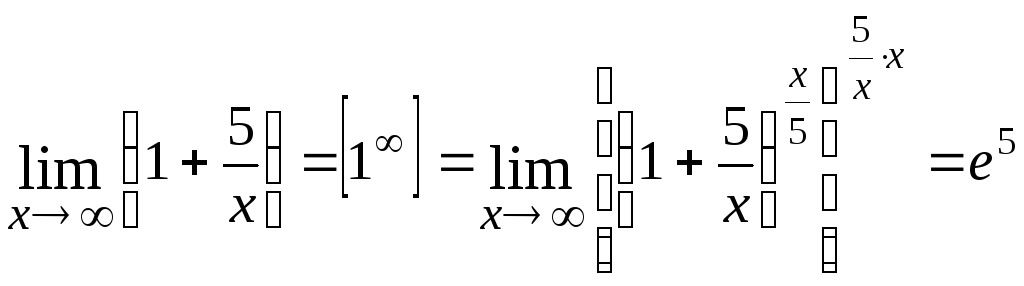
2.

3.
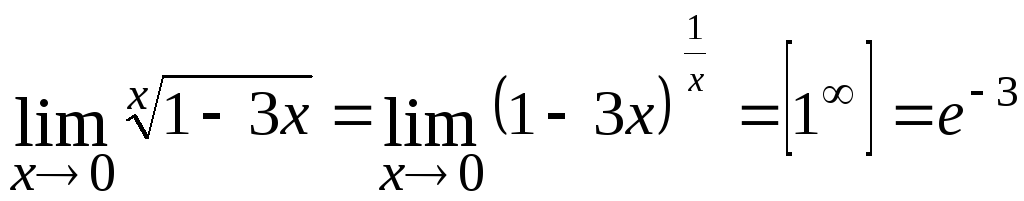
Если при
,
,
а,
то имеем неопределенность вида
.
Если
и
при
,
то имеет место неопределенность
.
Для раскрытия
неопределенностей вида
и
их преобразуют и сводят к неопределенности
видаследующим образом:

Примеры
Найти пределы
функций:
1.

2.

В заключение
отметим, что в дальнейшем будут рассмотрены
более эффективные методы вычисления
пределов функций, основанные на
использовании понятия производной.
Упражнения
Односторонние
пределы. Найти пределы:
1.

;

;
2.

;

0.
Непосредственное
вычисление пределов. Найти пределы:
3.
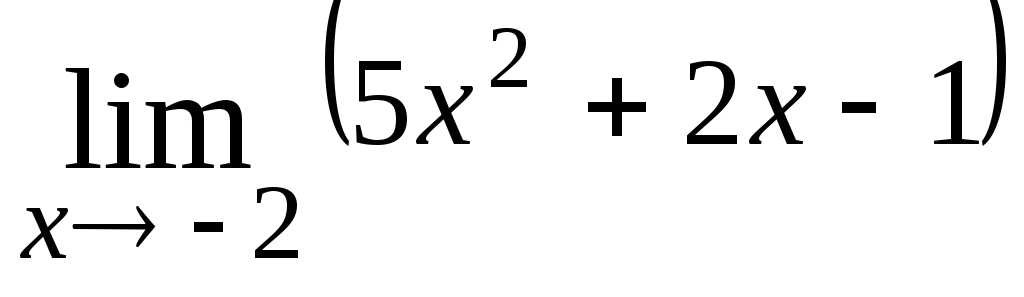
15;
4.

.
5.

0.
Раскрытие
неопределенности
.
Найти пределы:
6.
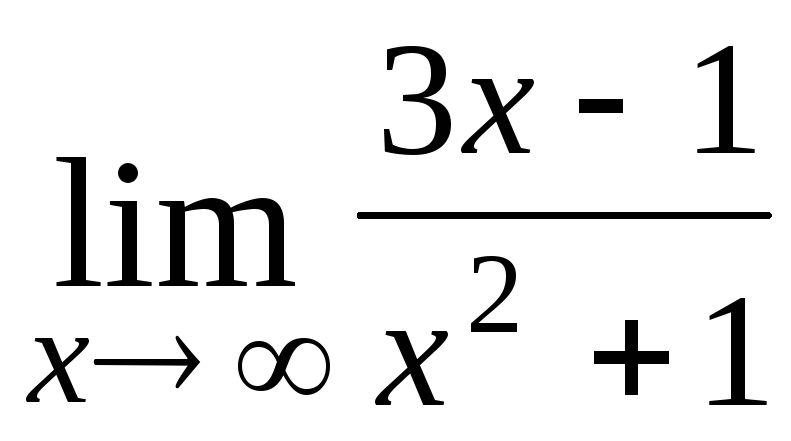
0;
7.
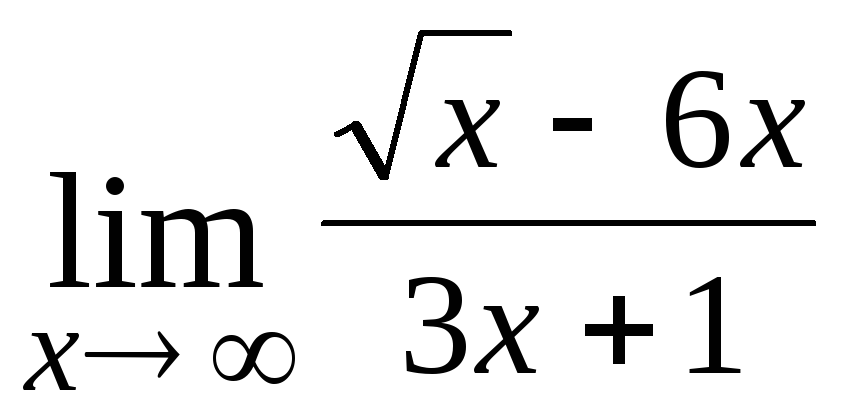
-2;
8.

;
9.

.
Раскрытие
неопределенности
.
Найти пределы:
10.

;
11.

-2;
12.
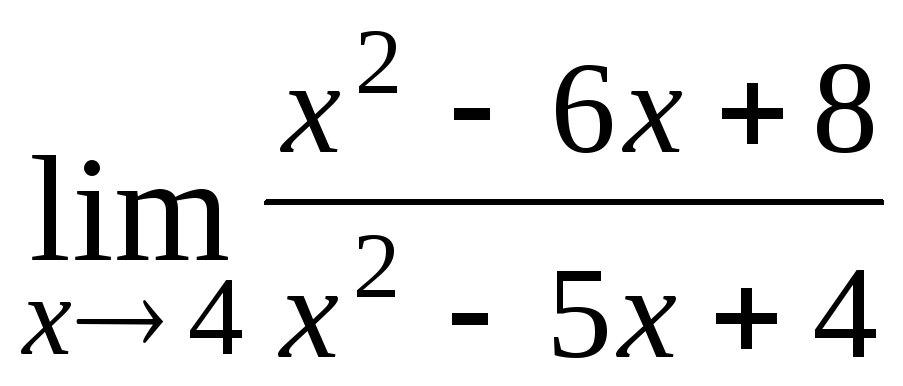
;
13.

;
14.

-12;
15.

.
16.
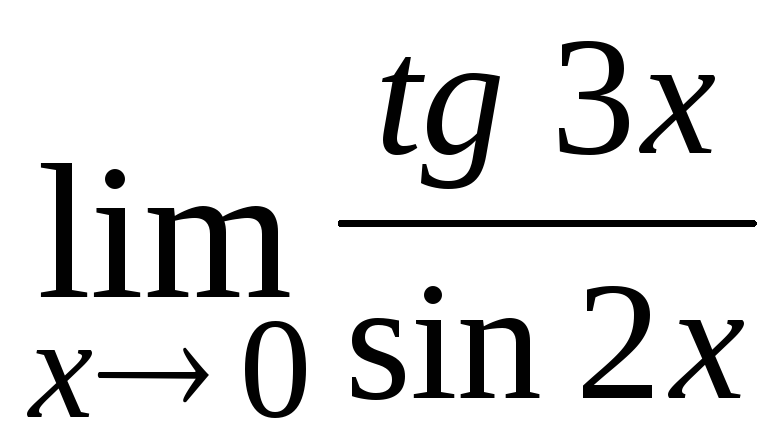
;
17.

;
18.

;
19.

;
20.

.
Раскрытие
неопределенностей
.
Найти пределы:
21.

;
22.

;
23.

0;
24.
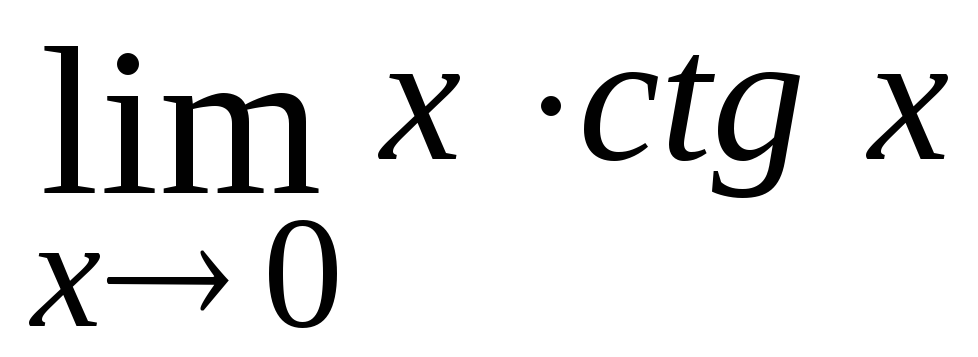
1.
Раскрытие
неопределенности.
Найти пределы:
25.
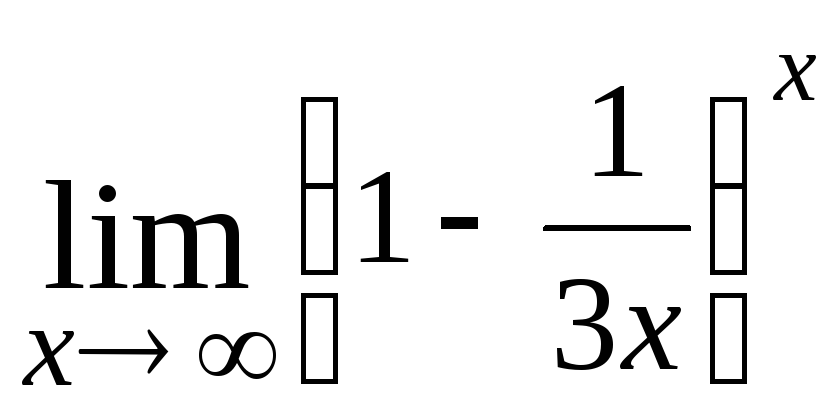
;
26.

;
27.

;
28.

.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Виды и правила раскрытия неопределенностей (Таблица)
|
Вид неопределенности |
Правило раскрытия |
|
1. |
1.1. Чтобы раскрыть неопределенность вида заданную отношением двух многочленов, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени. |
|
1.2. Для раскрытия неопределенности вида заданную отношением иррациональных функций, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени с учетом степеней корней. |
|
|
2. |
2.1. Для того, чтобы определить предел дробно-рациональной функции в случае, когда при x → a числитель и знаменатель дроби имеют пределы, равные нулю, надо числитель и знаменатель дроби разделить на x — a и перейти к пределу. Если и после этого числитель и знаменатель новой дроби имеют пределы, равные нулю при x → a, то надо произвести повторное деление на x — a. |
|
2.2. Чтобы раскрыть неопределенность вида в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности, умножив и числитель и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби. В случае квадратных корней и числитель и знаменатель дроби умножаются на сопряженное выражение тому, которое содержит иррациональность и применяется формула a2 – b2 = (a – b)(a + b) . В случае кубических корней и числитель и знаменатель дроби умножаются на неполный квадрат суммы или разности и применяется формула a3 ± b3 = (a ± b)(a2 ± ab + b2). |
|
|
3. |
3.1. Неопределенность вида получающаяся в результате алгебраической суммы иррациональных выражений, устраняется или приводится к типу 1 путем домножения и деления на одно и то же выражение, приводящее к формулам сокращенного умножения. В случае квадратных корней разность домножается на сопряженное выражение и применяется формула a2 – b2 = (a – b)(a + b) . В случае кубических корней функция домножается на неполный квадрат суммы или разности и применяется формула a3 ± b3 = (a ± b)(a2 ± ab + b2). |
|
3.2. Неопределенность вида получающаяся в результате алгебраической суммы двух дробей, устраняется или сводится к типу 2 Пусть:
Тогда: |
|
|
4. Замечательные пределы |
4.1. Первый замечательный предел (неопределенность В случае, когда под знаком предела стоят тригонометрические функции, дающие неопределенность
Его различные формы: |
|
4.2. Второй замечательный предел (неопределенность
Его различные формы:
|
|
|
5. |
5.1. Неопределенность вида сводится либо к неопределенности типа 1 Пусть
Тогда: |
|
6. |
6.1. Неопределенности вида сводятся к неопределенности типа 5 |


















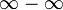 ,
, 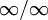 ,
,  ,
,  ,
, 


 ,
, ,
, ,
,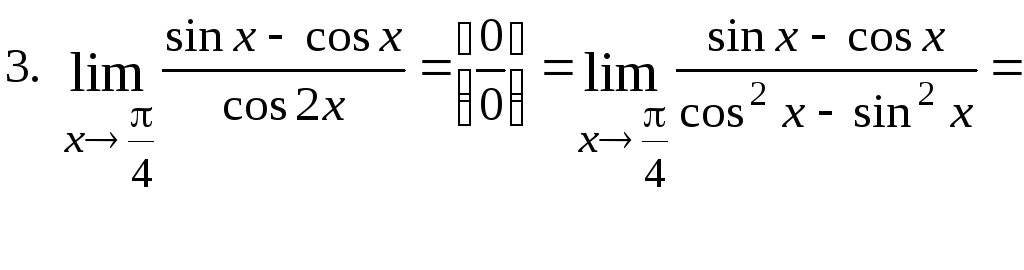













 ,
, ,
,  ,
, ,
,  .
. .
. ,
,  ,
,  ,
,  ,
, 
 , либо к неопределенности типа 2
, либо к неопределенности типа 2  путем перемещения в знаменатель одного из сомножителей.
путем перемещения в знаменатель одного из сомножителей.