Периметр как пишется знак

Периметр – это границы измерений

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Сегодня мы подробно расскажем, что такое ПЕРИМЕТР, как он считается и каково его практическое применение.

Материал этот изучают в начальных классах школы, но далеко не всегда получается понятно объяснить простые вещи.

Что такое периметр

Периметр – это общая граница любой плоской геометрической фигуры. Измеряется в тех же величинах, что и стороны многоугольников.

У окружности тоже есть периметр. Хотя само слово в этом случае не применяют, говоря – длина окружности. Интересно, что само слово ПЕРИМЕТР изначально и обозначало окружность.

Так оно переводится с древнегреческого «περίμετρον». Но другой, более общий перевод – «измеряю вокруг», и тогда он подходит под все плоские геометрические фигуры как окружность, так и многоугольники.

Расчет периметра многоугольников

Считать периметр многоугольников очень просто. Надо всего лишь сложить длины всех сторон. И неважно, насколько замысловато выглядят сами фигуры.

Рассмотрим периметры самых популярных фигур.

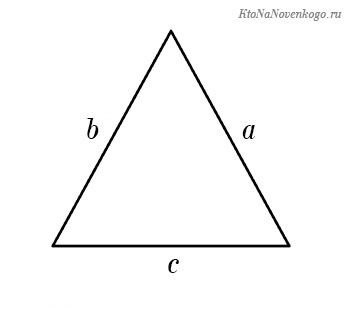
Периметр треугольника

Как мы уже сказали, для расчета периметра треугольника надо просто сложить все его стороны.

Периметр обозначается латинской буквой «P». Он будет равен:

P = a + b + c

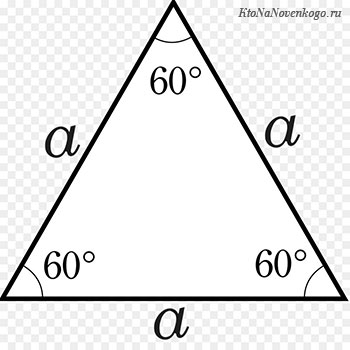
А если треугольник равносторонний или как его еще называют – правильный, то формула заметно упрощается.

P = a + a + a = 3a

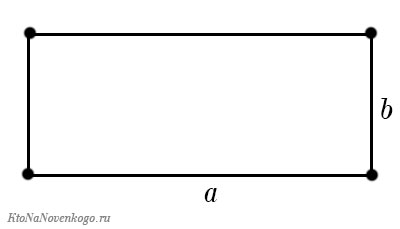
Периметр прямоугольника

Отличительная черта прямоугольника – его противоположные стороны равны.

P = a + b + a + b = 2a + 2b = 2 (a + b)

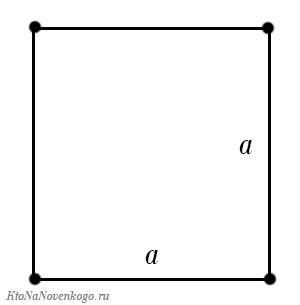
Как и у треугольника, у прямоугольника есть частный случай, когда всего его стороны равны между собой. И всем известно, что называется такая фигура – квадрат.

P = a + a + a + a = 4a

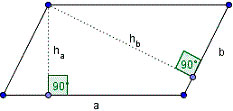
Периметр параллелограмма

Если кто забыл, то параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны между собой.

И периметр у него считается точно так же, как и у прямоугольника. Более того, прямоугольник – это частный случай параллелограмма.

P = a + a + b + b = 2a + 2b = 2 (a + b)

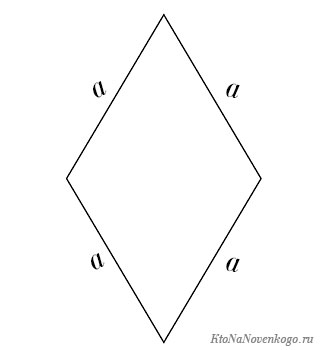
У параллелограмма есть еще один частный случай. Фигура, у которой все стороны равны. И называется она – ромб.

Его периметр считается точно так же, как и у квадрата.

P = a + a + a + a = 4a

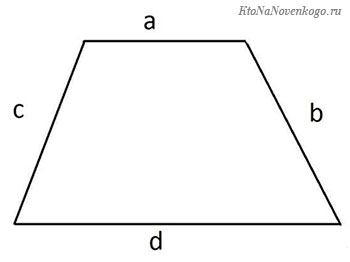
Периметр трапеции

И еще одна фигура, которая частенько встречается в жизни. И ее изучению посвящены отдельные главы школьной программы. Трапеция – это четырехугольник, у которого только две стороны лежат на параллельных прямых.

P = a + b + c + d

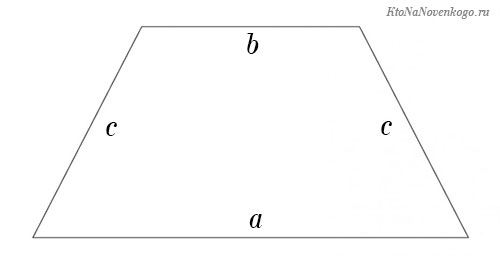
Но есть и частный случай, который называется равнобедренной трапецией. У этой фигуры непараллельные стороны равны между собой и идут под одинаковым наклоном.

P = a + b + c + c = a + b + 2c

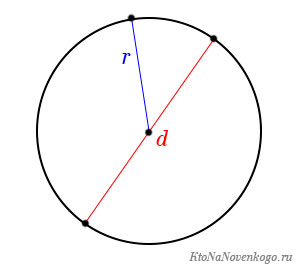
Расчет длины окружности

Для расчета длины окружности, которая, по сути, и является периметром фигуры, есть своя формула. Вот только эту величину, в отличие от многоугольников, принято обозначать латинской буквой «L».

L = 2 π r

В этой формуле букой r обозначается радиус окружности, то есть расстояние от ее центра до границы. А буква π – это математическая постоянная, которая равна 3,14 (хотя на самом деле число знаков после запятой бесконечно).

Вместо заключения

Для чего в жизни нужно знать про ПЕРИМЕТР? Приведем самый простой пример.

Если вы на даче соберетесь поставить забор, вам нужно будет точно знать, сколько материала покупать. Для этого вы измерите свой участок по длине и ширине. Как правило, дачные участки имеют форму прямоугольников. Соответственно, после этого легко будет посчитать периметр:

P = 2L + 2W

где L – длина участка, а W – ширина. И уже с этими расчетами вы можете смело ехать в строительный магазин.

Источник

Perimeter is the distance around a two dimensional shape, a measurement of the distance around something; the length of the boundary.

A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length. The perimeter of a circle or an ellipse is called its circumference.

Calculating the perimeter has several practical applications. A calculated perimeter is the length of fence required to surround a yard or garden. The perimeter of a wheel/circle (its circumference) describes how far it will roll in one revolution. Similarly, the amount of string wound around a spool is related to the spool’s perimeter; if the length of the string was exact, it would equal the perimeter.

Formulas

shape	formula	variables
circle		where is the radius of the circle and is the diameter.
triangle		where , and are the lengths of the sides of the triangle.
square/rhombus		where is the side length.
rectangle		where is the length and is the width.
equilateral polygon		where is the number of sides and is the length of one of the sides.
regular polygon	$2nbsin left({frac {pi }{n}}right)$	where is the number of sides and is the distance between center of the polygon and one of the vertices of the polygon.
general polygon	$a_{1}+a_{2}+a_{3}+cdots +a_{n}=sum _{{i=1}}^{n}a_{i}$	where $a_{i}$ is the length of the -th (1st, 2nd, 3rd … nth) side of an n-sided polygon.

The perimeter is the distance around a shape. Perimeters for more general shapes can be calculated, as any path, with ${textstyle int _{0}^{L}mathrm {d} s}$ , where is the length of the path and is an infinitesimal line element. Both of these must be replaced by algebraic forms in order to be practically calculated. If the perimeter is given as a closed piecewise smooth plane curve ${displaystyle gamma :[a,b]to mathbb {R} ^{2}}$ with

${displaystyle gamma (t)={begin{pmatrix}x(t)\y(t)end{pmatrix}}}$

then its length can be computed as follows:

${displaystyle L=int _{a}^{b}{sqrt {x'(t)^{2}+y'(t)^{2}}},mathrm {d} t}$

A generalized notion of perimeter, which includes hypersurfaces bounding volumes in -dimensional Euclidean spaces, is described by the theory of Caccioppoli sets.

Polygons

Perimeter of a rectangle.

Polygons are fundamental to determining perimeters, not only because they are the simplest shapes but also because the perimeters of many shapes are calculated by approximating them with sequences of polygons tending to these shapes. The first mathematician known to have used this kind of reasoning is Archimedes, who approximated the perimeter of a circle by surrounding it with regular polygons.

The perimeter of a polygon equals the sum of the lengths of its sides (edges). In particular, the perimeter of a rectangle of width and length ell equals

An equilateral polygon is a polygon which has all sides of the same length (for example, a rhombus is a 4-sided equilateral polygon). To calculate the perimeter of an equilateral polygon, one must multiply the common length of the sides by the number of sides.

A regular polygon may be characterized by the number of its sides and by its circumradius, that is to say, the constant distance between its centre and each of its vertices. The length of its sides can be calculated using trigonometry. If R is a regular polygon’s radius and n is the number of its sides, then its perimeter is

$2nRsin left({frac {180^{{circ }}}{n}}right).$

A splitter of a triangle is a cevian (a segment from a vertex to the opposite side) that divides the perimeter into two equal lengths, this common length being called the semiperimeter of the triangle. The three splitters of a triangle all intersect each other at the Nagel point of the triangle.

A cleaver of a triangle is a segment from the midpoint of a side of a triangle to the opposite side such that the perimeter is divided into two equal lengths. The three cleavers of a triangle all intersect each other at the triangle’s Spieker center.

Circumference of a circle

If the diameter of a circle is 1, its circumference equals π.

The perimeter of a circle, often called the circumference, is proportional to its diameter and its radius. That is to say, there exists a constant number pi, π (the Greek p for perimeter), such that if P is the circle’s perimeter and D its diameter then,

In terms of the radius r of the circle, this formula becomes,

To calculate a circle’s perimeter, knowledge of its radius or diameter and the number π suffices. The problem is that π is not rational (it cannot be expressed as the quotient of two integers), nor is it algebraic (it is not a root of a polynomial equation with rational coefficients). So, obtaining an accurate approximation of π is important in the calculation. The computation of the digits of π is relevant to many fields, such as mathematical analysis, algorithmics and computer science.

Perception of perimeter

The more one cuts this shape, the lesser the area and the greater the perimeter. The convex hull remains the same.

The perimeter and the area are two main measures of geometric figures. Confusing them is a common error, as well as believing that the greater one of them is, the greater the other must be. Indeed, a commonplace observation is that an enlargement (or a reduction) of a shape make its area grow (or decrease) as well as its perimeter. For example, if a field is drawn on a 1/10,000 scale map, the actual field perimeter can be calculated multiplying the drawing perimeter by 10,000. The real area is 10,000² times the area of the shape on the map. Nevertheless, there is no relation between the area and the perimeter of an ordinary shape. For example, the perimeter of a rectangle of width 0.001 and length 1000 is slightly above 2000, while the perimeter of a rectangle of width 0.5 and length 2 is 5. Both areas are equal to 1.

Proclus (5th century) reported that Greek peasants «fairly» parted fields relying on their perimeters.^[1] However, a field’s production is proportional to its area, not to its perimeter, so many naive peasants may have gotten fields with long perimeters but small areas (thus, few crops).

If one removes a piece from a figure, its area decreases but its perimeter may not. In the case of very irregular shapes, confusion between the perimeter and the convex hull may arise. The convex hull of a figure may be visualized as the shape formed by a rubber band stretched around it. In the animated picture on the left, all the figures have the same convex hull; the big, first hexagon.

Isoperimetry

The isoperimetric problem is to determine a figure with the largest area, amongst those having a given perimeter. The solution is intuitive; it is the circle. In particular, this can be used to explain why drops of fat on a broth surface are circular.

This problem may seem simple, but its mathematical proof requires some sophisticated theorems. The isoperimetric problem is sometimes simplified by restricting the type of figures to be used. In particular, to find the quadrilateral, or the triangle, or another particular figure, with the largest area amongst those with the same shape having a given perimeter. The solution to the quadrilateral isoperimetric problem is the square, and the solution to the triangle problem is the equilateral triangle. In general, the polygon with n sides having the largest area and a given perimeter is the regular polygon, which is closer to being a circle than is any irregular polygon with the same number of sides.

Etymology

The word comes from the Greek περίμετρος perimetros, from περί peri «around» and μέτρον metron «measure».

References

^ Heath, T. (1981). A History of Greek Mathematics. Vol. 2. Dover Publications. p. 206. ISBN 0-486-24074-6.

External links

Look up perimeter in Wiktionary, the free dictionary.

Weisstein, Eric W. «Perimeter». MathWorld.
Weisstein, Eric W. «Semiperimeter». MathWorld.

Источник

Perimeter is the distance around a two dimensional shape, a measurement of the distance around something; the length of the boundary.

Formulas

shape	formula	variables
circle		where is the radius of the circle and is the diameter.
triangle		where , and are the lengths of the sides of the triangle.
square/rhombus		where is the side length.
rectangle		where is the length and is the width.
equilateral polygon		where is the number of sides and is the length of one of the sides.
regular polygon	$2nbsin left({frac {pi }{n}}right)$	where is the number of sides and is the distance between center of the polygon and one of the vertices of the polygon.
general polygon	$a_{1}+a_{2}+a_{3}+cdots +a_{n}=sum _{{i=1}}^{n}a_{i}$	where $a_{i}$ is the length of the -th (1st, 2nd, 3rd … nth) side of an n-sided polygon.

${displaystyle gamma (t)={begin{pmatrix}x(t)\y(t)end{pmatrix}}}$

then its length can be computed as follows:

${displaystyle L=int _{a}^{b}{sqrt {x'(t)^{2}+y'(t)^{2}}},mathrm {d} t}$

A generalized notion of perimeter, which includes hypersurfaces bounding volumes in -dimensional Euclidean spaces, is described by the theory of Caccioppoli sets.

Polygons

Perimeter of a rectangle.

The perimeter of a polygon equals the sum of the lengths of its sides (edges). In particular, the perimeter of a rectangle of width and length ell equals

$2nRsin left({frac {180^{{circ }}}{n}}right).$

Circumference of a circle

If the diameter of a circle is 1, its circumference equals π.

In terms of the radius r of the circle, this formula becomes,

Perception of perimeter

The more one cuts this shape, the lesser the area and the greater the perimeter. The convex hull remains the same.

Isoperimetry

Etymology

The word comes from the Greek περίμετρος perimetros, from περί peri «around» and μέτρον metron «measure».

References

^ Heath, T. (1981). A History of Greek Mathematics. Vol. 2. Dover Publications. p. 206. ISBN 0-486-24074-6.

External links

Look up perimeter in Wiktionary, the free dictionary.

Weisstein, Eric W. «Perimeter». MathWorld.
Weisstein, Eric W. «Semiperimeter». MathWorld.

Источник

Практически каждый раз при решении задач по математике, физике или другим дисциплинам приходится выбирать обозначения тех или иных величин. Среди них следует различать обозначения общепринятые (или даже устанавливаемые нормативными документами) и обозначения, выбор которых обычно выполняется самостоятельно, в зависимости от индивидуальных предпочтений. Есть также величины, обозначения которых в разных дисциплинах приняты свои. Есть обозначения международные, а есть – принятые различными в разных странах.

Как обозначается длина, ширина, высота, толщина, глубина

Обозначение длины в математике обычно зависит от того, какой объект в данном случае рассматривается: одномерный, двумерный или трехмерный. Если речь идёт об обозначении длины одномерного объекта (нити, проволоки и т.п.) или обозначении длины куска сортового проката (трубы, швеллера, двутавра и т.п.), то длина обычно обозначается буквой l (написанной курсивом, т.е. с наклоном, чтобы не было похоже на «единицу») или L. Если же речь идёт о двумерном объекте, в котором нужно обозначить не только длину, но и ширину, то обычно принимают одну из таких пар обозначений: a и b (а – длина, b — ширина), l и b (l – длина, b — ширина), l и h (l – длина, h — высота). Для обозначений могут быть использованы и соответствующие заглавные буквы, в литературе часто встречается сочетание L, B, H (L – длина, В – ширина, Н — высота). Эти же буквы приняты и в физике для обозначения длины, ширины, высоты объектов. Если же речь идёт о длине волны, то она обозначается строчной греческой буквой «лямбда».

Высота обозначается обычно буквой h (читается: [аш]). В технической литературе для обозначения высоты также используют букву Н (читается: [аш]). Этими же буквами (h, реже Н) обозначается глубина.

Толщина в физике обозначается либо строчной (маленькой) буквой s, либо греческой строчной буквой «дельта», с использованием (при необходимости) нижних индексов (обычно – числовых, соответствующих номеру слоя, т.е. 1, 2, 3, 4 и т.д.).

Вопросы «как в математике пишется длина», «как в математике пишется периметр», «как в математике пишется площадь» некорректны. Здесь уместно вместо слова «пишется» употребить слово «обозначается».

Как обозначается периметр

При решении задач по геометрии часто возникает необходимость обозначить периметр. Периметр в математике обозначается заглавной (т.е. большой) буквой Р (читается: [пэ]).

Как обозначается площадь

Обозначение площади в научно-технической литературе можно встретить различные. Поэтому и возникают вопросы «Как обозначается площадь в математике», «Как обозначается площадь в физике» и т.п. Ответ на вопрос о том, какой буквой обозначается площадь, зависит от конкретной дисциплины, о которой в данный момент идёт речь. В математике и в физике площадь обозначается буквой S заглавной (читается: [эс]). Так, в геометрии этой буквой обозначается площадь любых фигур (треугольника, прямоугольника, квадрата, ромба и т.п.). Если нужно в одной задаче обозначить площадь нескольких фигур, то используются нижние индексы. В качестве индекса могут быть использованы числа (1, 2, 3 и т.д.), т.е. площади обозначаются как S₁, S₂, S₃ и т.д., а могут быть использованы сокращения от названия фигур (S_тр, S_пр, S_кв, S_р и т.п.). При необходимости обозначения в одной задаче площадей нескольких треугольников чаще в качестве нижнего индекса принимают обозначения этих треугольников (например, S_ABC, S_MNP, S_LPH со значком треугольника перед буквами ABC, MNP, LPH). В физике обозначается площадь поперечного сечения той же буквой S, при необходимости – с добавлением нижнего индекса (например, S₁, S₂, S₃ и т.д.). Однако, в сопромате и в строительной механике буквой S (с добавлением индекса) обозначается не площадь, а статический момент площади относительно оси, а для обозначения площади в этих дисциплинах обычно используются буквы F (читается: [эф]) и A (читается: [а]).

Источники информации:

Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра/ Под ред. П.Ф. Фильчакова
Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов
ru.wikipedia.org – список обозначений в физике

Источник

Периметр — длина контура замкнутой плоской фигуры, длина границы.

Пери́метр (др.-греч. περίμετρον — окружность, др.-греч. περιμετρέο — измеряю вокруг) — общая длина границы фигуры (чаще всего на плоскости). Имеет ту же размерность величин, что и длина.

Иногда периметром называют границу геометрической фигуры.

Вычисление периметра имеет существенное практическое значение. Например, для вычисления длины ограды вокруг сада или участка. Периметр колеса (окружности) определяет, насколько далеко оно продвинется при полном обороте. Таким же образом, длина нитки, намотанной на катушку, тесно связана с периметром катушки.

Содержание

1 Формулы
2 Многоугольники
3 Периметр окружности
4 Осмысление периметра
5 Изопериметрическая задача
6 Вариации и обобщения
7 См. также
8 Примечания
9 Литература
10 Ссылки

Формулы

фигура	формула	переменные
окружность		где — радиус окружности, а — диаметр.
треугольник		где , и — длины сторон треугольника.
квадрат/ромб		где — длина стороны.
прямоугольник		где — длина (основания), а — ширина.
равносторонний многоугольник		где — число сторон, а — длина сторон.
правильный многоугольник	${displaystyle 2nbsin left({frac {pi }{n}}right)}$	где — число сторон, а — расстояние от центра многоугольника до одной из вершин многоугольника.
общий многоугольник	${displaystyle a_{1}+a_{2}+a_{3}+cdots +a_{n}=sum _{i=1}^{n}a_{i}}$	где $a_{{i}}$ — длина -й (1, 2, 3 … n) стороны n-угольника.

Многоугольники

Многоугольники являются основными фигурами для определения периметров, и не только потому, что они являются простейшими фигурами, но и потому, что периметры многих фигур вычисляются путём аппроксимации их последовательностью многоугольников. Первым известным математиком, который использовал этот подход, был Архимед, который аппроксимировал периметр окружности путём описывания около неё правильных многоугольников.

Периметр многоугольника равен сумме длин его сторон. В частности, периметр прямоугольника, имеющего ширину и длину ell , равен .

Равносторонний многоугольник — это многоугольник, имеющий равные длины сторон (например ромб — это равносторонний многоугольник с 4 сторонами). Чтобы вычислить периметр равностороннего многоугольника, нужно умножить число сторон на общую длину стороны.

Периметр правильного многоугольника можно вычислить по числу сторон и его радиусу, то есть расстоянию от центра до вершин. Длину стороны можно вычислить, используя тригонометрию. Если R — радиус многоугольника, а n — число сторон, периметр равен

${displaystyle 2nRsin left({frac {180^{circ }}{n}}right).}$

Периметр окружности

Если диаметр окружности равен 1, её периметр равен π.

Периметр окружности пропорционален её диаметру (и радиусу). То есть, существует константа π такая, что если P — периметр окружности, а D — её диаметр, то:

Для радиуса r окружности формула превращается в

Для вычисления периметра окружности знание радиуса или диаметра и числа π достаточно. Проблема заключается в том, что π не является рациональным (его нельзя выразить в виде дроби двух целых чисел) и даже не является алгебраическим (оно не является корнем никакого полиномиального уравнения с рациональными коэффициентами). Таким образом, получение точного приближения к π важно для вычислений. Нахождение знаков π относится ко многим областям, таким как математический анализ и теория алгоритмов.

Осмысление периметра

Чем мельче структура фигуры, тем меньше площадь и тем больше периметр. Выпуклая оболочка остаётся той же самой.

Периметр и площадь являются двумя основными измерениями геометрических фигур, их часто путают. Нередко также считают, что увеличение одной из этих величин приводит к увеличению другой. Действительно, увеличение (или уменьшение) размера фигуры приводит к увеличению (или уменьшению) её площади, так же как и её периметра. Так, например, если нарисовать карту поля в масштабе 1/10 000, действительные размеры периметра можно вычислить простым умножением на 10 000. Действительная площадь будет в 10 000² раз больше площади фигуры на карте.

Тем не менее, нет никакой связи между площадью и периметром фигур. Например, периметр прямоугольника шириной 0,001 и длиной 1000 чуть больше 2000, в то время, как периметр прямоугольника шириной 0,5 и длиной 2 равен 5. Площади обеих фигур равны 1.

Прокл (V-й век) писал, что греческие крестьяне делили поля, опираясь на периметры^[1], однако урожай с поля пропорционален площади, а не периметру, и много наивных крестьян получали поля с большим периметром, но малой площадью.

Если удалить часть фигуры, её площадь уменьшится, а вот периметр может и не уменьшиться. В случае очень неправильных фигур некоторые могут спутать периметр с выпуклой оболочкой. Выпуклую оболочку визуально можно представить как резинку, натянутую вокруг фигуры. На рисунке слева все фигуры имеют одну выпуклую оболочку (шестиугольник).

Изопериметрическая задача

Изопериметрическая задача — это задача нахождения фигуры с максимальной площадью среди фигур, имеющих заданный периметр.
Решение интуитивно — это окружность. В частности поэтому капли жира в бульоне имеют форму кружочков.

Задача выглядит простой, но строгое математическое доказательство сложно. Изопериметрическая задача иногда упрощается — найти четырёхугольник, треугольник или другую определённую фигуру с наибольшей площадью среди имеющих заданный периметр. Решение изопериметрической задачи для четырёхугольников — квадрат, для треугольников — правильный треугольник. В общем случае, многоугольник с n сторонами имеет максимальную площадь при заданном периметре, если он является правильным, что ближе к окружности по сравнению с неправильными многоугольниками.

Вариации и обобщения

Полупериметр — половина периметра. Употребляется в основном в геометрии треугольника.

См. также

Длина кривой
Площадь фигуры
Задача Дидоны
Множество Каччопполи^[en]
Парадокс береговой линии
Изопериметрическая задача
Теорема Пифагора
Смоченный периметр

Примечания

↑ Heath, 1981, с. 206.

Литература

T. Heath. A History of Greek Mathematics. — Dover Publications, 1981. — Т. 2. — ISBN 0-486-24074-6.

Ссылки

Weisstein, Eric W. Perimeter (англ.) на сайте Wolfram MathWorld.
Weisstein, Eric W. Semiperimeter (англ.) на сайте Wolfram MathWorld.

Источник

Периметр – это границы измерений

Что такое периметр

Расчет периметра многоугольников

Периметр треугольника

Периметр прямоугольника

Периметр параллелограмма

Периметр трапеции

Расчет длины окружности

Вместо заключения

Formulas

Polygons

Circumference of a circle

Perception of perimeter

Isoperimetry

Etymology

See also

References

External links

Formulas

Polygons

Circumference of a circle

Perception of perimeter

Isoperimetry

Etymology

See also

References

External links

Содержание

Формулы

Многоугольники

Периметр окружности

Осмысление периметра

Изопериметрическая задача

Вариации и обобщения

См. также

Примечания

Литература

Ссылки