История возникновения координат на
плоскости
История возникновения координат и
системы координат начинается очень
давно, первоначально идея метода
координат возникла ещё в древнем мире
в связи с потребностями астрономии,
географии, живописи. Древнегреческого
ученого Анаксимандра Милетского (ок.
610-546 до н. э.) считают составителем первой
географической карты. Он четко описывал
широту и долготу места, используя
прямоугольные проекции.
Более чем за 100 лет до н.э греческий
ученый Гиппарх предложил опоясать на
карте земной шар параллелями и меридианами
и ввести теперь хорошо известные
географические координаты: широту и
долготу и обозначить их числами.
Идея изображать числа в виде точек, а
точкам давать числовые обозначения
зародилась в далекой древности.
Первоначальное применение координат
связано с астрономией и географией, с
потребностью определять положение
светил на небе и определенных пунктов
на поверхности Земли, при составлении
календаря, звездных и географических
карт. Следы применения идеи прямоугольных
координат в виде квадратной сетки
(палетки) изображены на стене одной из
погребальных камер Древнего Египта.
Основная заслуга в создании современного
метода координат принадлежит французскому
математику Рене Декарту. До наших времён
дошла такая история, которая подтолкнула
его к открытию. Занимая в театре места,
согласно купленным билетам, мы даже не
подозреваем, кто и когда предложил
ставший обычным в нашей жизни метод
нумерации кресел по рядам и местам.
Оказывается эта идея осенила знаменитого
философа, математика и естествоиспытателя
Рене Декарта (1596-1650)– того самого, чьим
именем названы прямоугольные координаты.
Посещая парижские театры, он не уставал
удивляться путанице, перебранкам, а
подчас и вызовам на дуэль, вызываемыми
отсутствием элементарного порядка
распределения публики в зрительном
зале. Предложенная им система нумерации,
в которой каждое место получало номер
ряда и порядковый номер от края, сразу
сняла все поводы для раздоров и произвела
настоящий фурор в парижском высшем
обществе.
Научное описание прямоугольной системы
координат Рене Декарт впервые сделал
в своей работе «Рассуждение о методе»
в 1637 году. Поэтому прямоугольную систему
координат называют также — Декартова
система координат. Кроме того, в своей
работе «Геометрия» (1637), открывшей
взаимопроникновение алгебры и геометрии,
Декарт ввел впервые понятия переменной
величины и функции. «Геометрия» оказала
огромное влияние на развитие математики.
В декартовой системе координат получили
реальное истолкование отрицательные
числа.
Кроме математики интересы Декарта
распространялись на физику, где он дал
четкую формулировку закона инерции,
открыл закон преломления световых лучей
на границе двух различных сред
(«Диоптрика», 1637).
Вклад в развитие координатного метода
внес также Пьер Ферма, однако его работы
были впервые опубликованы уже после
его смерти. Декарт и Ферма применяли
координатный метод только на плоскости.
Координатный метод для трёхмерного
пространства впервые применил Леонард
Эйлер уже в XVIII веке.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
КООРДИНАТНАЯ ПЛОСКОСТЬ
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
В речи взрослых вы могли слышать такую фразу: «Оставьте мне ваши координаты». Это выражение означает, что собеседник должен оставить свой адрес или номер телефона, по которым его можно найти. Те из вас, кто играл в «морской бой», пользовались при этом соответствующей системой координат. Аналогичная система координат используется в шахматах. Места в зрительном зале кинотеатра задают двумя числами: первым числом обозначают номер ряда, а вторым — номер кресла в этом ряду. Идея задавать положение точки на плоскости с помощью чисел зародилась ещё в древности. Система координат пронизывает всю практическую жизнь человека и имеет огромное практическое применение. Поэтому мы решили создать данный проект, чтобы расширить свои познания по теме «Координатная плоскость»
Задачи проекта:
-
ознакомиться с историей возникновения прямоугольной системой координат на плоскости;
выдающимися деятелями, занимающимися данной темой;
-
найти интересные исторические факты;
-
хорошо воспринимать на слух координаты; четко и аккуратно выполнять построения;
-
подготовить презентацию.
ГлаваI. Координатная плоскость
Идея задавать положение точки на плоскости с помощью чисел зародилась ещё в древности – прежде всего у астрономов и географов при составлении звёздных и географических карт, календарей.
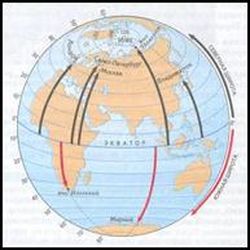
§1. Зарождение координат. Система координат в географии
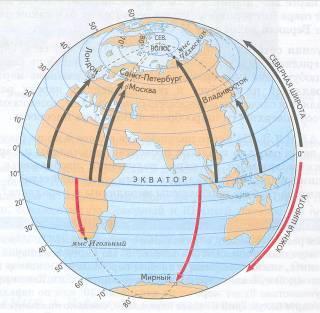
За 200 лет до нашей эры греческий ученый Гиппарх ввёл географические координаты. Он предложил нарисовать на географической карте параллели и меридианы и обозначить числами широту и долготу. С помощью этих двух чисел можно точно определить положение острова, поселка, горы или колодца в пустыне и нанести их на карту или глобус, Научившись определять в открытом мире широту и долготу местонахождения корабля, моряки получили возможность выбирать нужное им направление.
Восточную долготу и северную широту обозначают числами со знаком «плюс», а западную долготу и южную широту — со знаком «минус». Таким образом, пара чисел со знаками однозначно определяет точку на земном шаре.
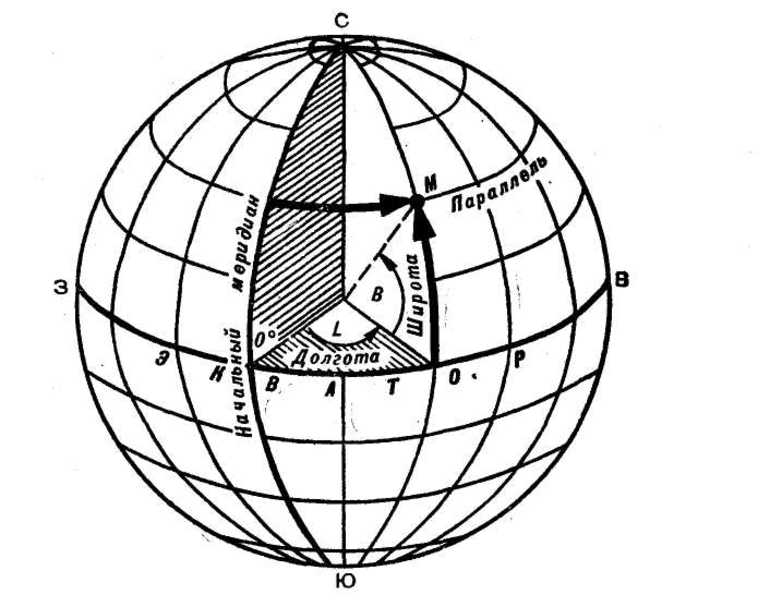
Географическая широта ? — угол между отвесной линией в данной точке и плоскостью экватора, отсчитываемый от 0 до 90 в обе стороны от экватора. Географическая долгота ? — угол между плоскостью меридиана, проходящего через данную точку, и плоскостью начала меридиана(см. Гринвичский меридиан). Долготы от 0 до 180 к востоку от начала меридиана называют восточными, к западу – западными.
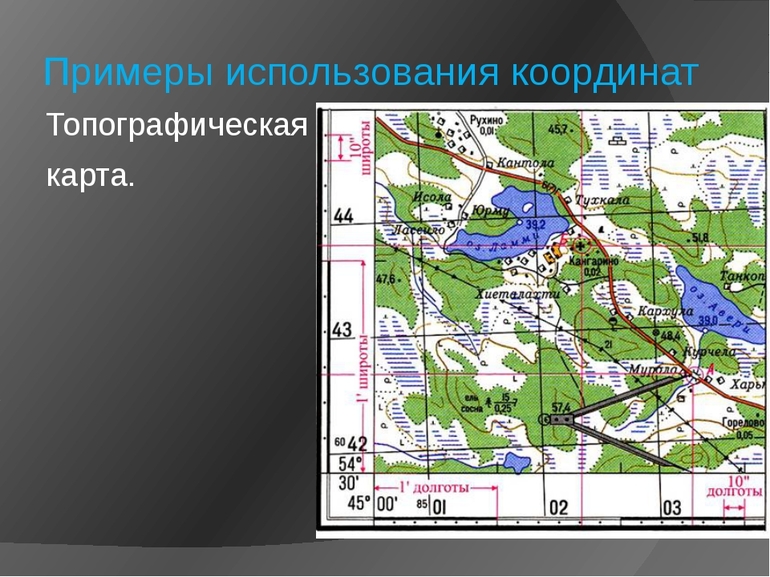
Чтобы найти некоторый объект в городе, в большинстве случаев достаточно знать его адрес. Трудности возникают, если нужно объяснить, где находится, например, дачный участок, место в лесу. Универсальным средством указания местоположения служат географические координаты.
При попадании в аварийную ситуацию, человек первым делом должен уметь ориентироваться на местности. Иногда необходимо определить географические координаты своего местоположения, например, чтобы передать спасательной службе или для других целей.
В современной навигации стандартно используется всемирная система координат WGS-84. В этой системе координат работают все GPS навигаторы и основные картографические проекты в Интернете. Координаты в системе WGS-84 столь же общеупотребимы и понятны всем, как всемирное время. Общедоступная точность при работе с географическими координатами составляет 5 — 10 метров на местности.
Географические координаты представляют собой числа со знаком (широта от -90° до +90°, долгота от -180° до +180°) и могут записываться в различных формах: в градусах (ddd.ddddd°); градусах и минутах (ddd° mm.mmm’); градусах, минутах и секундах (ddd° mm’ ss.s»). Формы записи могут быть элементарно пересчитаны одна в другую (1 градус = 60 минут, 1 минута = 60 секунд). Для обозначения знака координат часто используются буквы, по названию сторон света: N и E — северная широта и восточная долгота — положительные числа, S и W — южная широта и западная долгота — отрицательные числа.
Форма записи координат в ГРАДУСАХ наиболее удобна для ручного ввода и совпадает с математической записью числа. Форма записи координат в ГРАДУСАХ И МИНУТАХ является предпочтительной во многих случаях, такой формат установлен по умолчанию в большинстве GPS навигаторов и стандартно используется в авиации и на море. Классическая форма записи координат в ГРАДУСАХ, МИНУТАХ И СЕКУНДАХ в действительности не находит большого практического применения.
§2. Система координат в астрономии. Мифы о созвездиях
Как было сказано выше идея задавать положение точки на плоскости с помощью чисел зародилась в древности у астрономов при составлении звездных карт . Людям нужно было считать время, предсказывать сезонные явления (приливы, отливы, сезонные дожди, затопления), нужно было ориентироваться на местности во время путешествий.
Астрономия – это наука о звёздах, планетах, небесных телах, их строении и развитии.
Прошли тысячи лет, наука шагнула далеко вперёд, а человек по-прежнему не может оторвать восхищённого взгляда от красоты ночного неба.
Созвездия – участки звёздного неба, характерные фигуры, образуемые яркими звёздами. Всё небо разделено на 88 созвездий, которые облегчают ориентирование среди звёзд. Большинство названий созвездий пришло из древности.
Самое известное созвездие – Большая Медведица. В Древнем Египте его называли “Гиппопотам”, а казахи называли “Конь на привязи”, хотя внешне созвездие не напоминает ни одного, ни другого животного. Какое же оно?
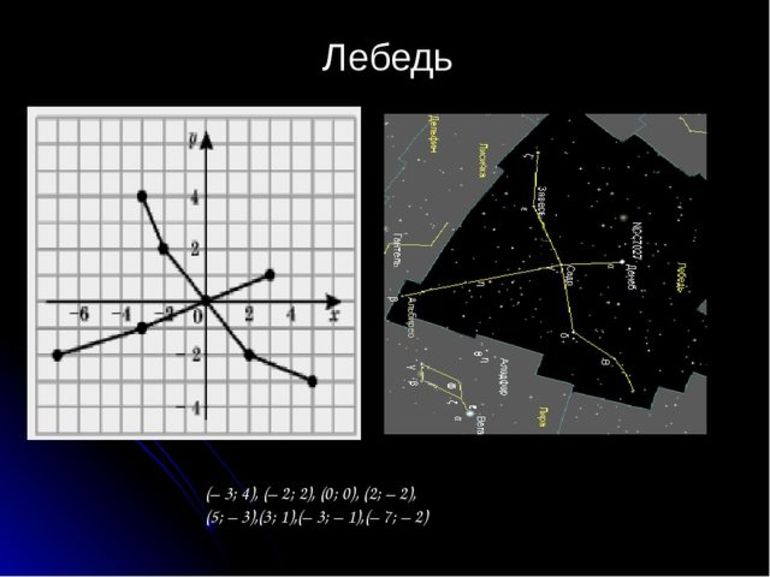
У древних греков существовала легенда о созвездиях Большой и Малой Медведиц. Всемогущий бог Зевс решил взять себе в жены прекрасную нимфу Калисто, одну из служанок богини Афродиты, вопреки желанию последней. Чтобы избавить Калисто от преследований богини, Зевс обратил Калисто в Большую медведицу, ее любимую собаку – в Малую Медведицу и взял их на небо. Перенести созвездия Большой и Малой Медведиц со звездного неба на координатную плоскость. . Каждая из звёзд “ Ковша большой медведицы” имеет свое название.
МЕДВЕДИЦУ БОЛЬШУЮ
Узнаю по КОВШУ я!
Семь звёзд сверкают тут,
А вот как их зовут:
ДУБХЕ освещает мрак,
Рядом с ним горит МЕРАК,
Сбоку ФЕКДА с МЕГРЕЦОМ,
Разудалым молодцом.
От МЕГРЕЦА на отлёт
Расположен АЛИОТ,
А за ним — МИЦАР с АЛЬКОРОМ
(Эти двое светят хором).
Замыкает ковшик наш
Бесподобный БЕНЕТНАШ.
Он указывает глазу
Путь в созвездье ВОЛОПАСА,
Где АРКТУР прекрасный светит,
Всяк теперь его заметит!
Не менее красивая легенда о созвездиях « Цефея», «Кассиопеи» и «Андромеды» .
Когда-то Эфиопией правил царь Цефей. Однажды его супруга, царица Кассиопея, имела неосторожность похвастать своей красотой перед обитательницами моря — нереидами. Последние, обидевшись, пожаловались богу моря Посейдону, и разгневанный дерзостью Кассиопеи властитель морей напустил на берега Эфиопии морское чудовище – Кита. Чтобы избавить свое царство от разрушений, Цефей, по совету оракула, решил принести жертву чудовищу и отдать ему на съедение свою любимую дочь Андромеду. Он приковал Андромеду к прибрежной скале и оставил ее в ожидании решения своей участи.
А в это время на другом краю света мифический герой Персей совершил смелый подвиг. Он проник на уединенный остров, где жили горгоны – удивительные чудовища в образе женщин, у которых на головах вместо волос кишели змеи. Взгляд горгон был так ужасен, что каждый на кого они смотрели, мгновенно превращался в камень.
Воспользовавшись сном этих чудовищ, Персей отсек голову одной из них –Горгоне Медузе. В этот момент из отрубленного тела Медузы выпорхнул конь Пегас. Персей схватил голову медузы, вскочил на Пегаса и по воздуху помчался к себе на родину. Когда он пролетал над Эфиопией, то увидел прикованную к скале Андромеду. В этот момент Кит уже вынырнул из морских пучин, готовясь проглотить свою жертву. Но Персей, ринувшись в смертельный бой с Китом, победил чудовище. Он показал Киту еще не потерявшую силу голову медузы, и чудовище окаменело, превратившись в остров. Что же касается Персея, то, расковав Андромеду , он вернул ее отцу, а растроганный от счастья Цефей отдал Андромеду в жены Персею. Так благополучно закончилась эта история, главные герои которой были помещены древними греками на небо.
На звездной карте можно найти не только Андромеду с ее отцом, матерью и мужем, но и волшебного коня пегаса и виновника всех бед — чудовища Кита.
Созвездие Кита расположено ниже Пегаса и Андромеды. К сожалению, оно не отмечено какими-нибудь характерными яркими звездами и поэтому принадлежит к числу второстепенных созвездий.
§3. Использование идеи прямоугольных координат в живописи.
Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта. В погребальной камере пирамиды отца Рамсеса на стене имеется сеть квадратиков. С их помощью перенесено изображение в увеличенном виде. Прямоугольной сеткой пользовались и художники Возрождения.
Рис.3
Слово «перспектива» в переводе с латинского означает «ясно вижу». В изобразительном искусстве линейная перспектива — это изображение предметов на плоскости в соответствии с кажущимися изменениями их величины. Основу современной теории перспективы заложили великие художники эпохи Возрождения — Леонардо да Винчи, Альбрехт Дюрер и другие. На одной из гравюр Дюрера (рис. 3) изображён способ рисования с натуры через стекло с нанесённой на него квадратной сеткой. Этот процесс можно описать так: если встать перед окном и, не изменяя точки зрения, обвести на стекле всё, что видно за ним, то полученный рисунок и будет перспективным изображением пространства.
Египетские методы проектирования, которые, похоже, основывались на схемах квадратной сетки. В египетском искусстве имеются многочисленные примеры, показывающие, что художники и скульпторы сначала рисовали сетку на стене, которую предстояло расписать или вырезать, для того чтобы сохранить установленные пропорции. Простые числовые отношения этих сеток служат сердцевиной всех великих художественных произведений египтян.
Тот же метод использовался многими художниками Возрождения, в том числе и Леонардо да Винчи. В Древнем Египте это нашло свое воплощение в Великой пирамиде, что и подкрепляется ее тесной связью с узором на Марлборо-Дауне.
Приступая к работе, египетский художник расчерчивал стену сеткой прямых линий и затем тщательно переносил на нее фигуры. Но геометрическая упорядоченность не мешала ему воссоздавать натуру с детальной точностью. Наружность каждой рыбы, каждой птицы передана с такой правдивостью, что современные зоологи без труда определяют их виды. На рис.4 дана деталь композиции с иллюстрации- дерево с птицами, схваченными сетью Хнумхотепа. Движение руки художника направлялось не только запасами его навыков, но и глазом, чувствительным к очертаниям натуры.
Рис.4 Птицы на акации
Глава II. Метод координат в математике
§1. Применение координат в математике. Заслуги
французского математика Рене Декарта
Долгое время лишь география «землеописание» — пользовалась этим замечательным изобретением, и только в 14 веке французский математик Никола Орем (1323-1382) попытался приложить его к «землеизмерению» — геометрии. Он предложил покрыть плоскость прямоугольной сеткой и называть широтой и долготой то, что мы теперь называем абсциссой и ординатой.
На основе этого удачного нововведения возник метод координат, связавший геометрию с алгеброй. Основная заслуга в создании этого метода принадлежит великому французскому математику Рене Декарту (1596 — 1650). В его честь такая система координат называется декартовой, обозначающая место любой точки плоскости расстояниями от этой точки до «нулевой широты» — оси абсцисс » и «нулевого меридиана» — оси ординат.
Однако этот гениальный французский ученый и мыслитель XVII века (1596 — 1650) далеко не сразу нашел свое место в жизни. Родившись в дворянской семье, Декарт получил хорошее образование. В 1606 году отец отправил его в иезуитскую коллегию Ла Флеш. Учитывая не очень крепкое здоровье Декарта, ему делали некоторые послабления в строгом режиме этого учебного заведения, например, разрешали вставать позже других. Приобретя в коллегии немало познаний, Декарт в то же время проникся антипатией к схоластической философии, которую он сохранил на всю свою жизнь.
После окончания коллегии Декарт продолжил образование. В 1616 в университете Пуатье он получил степень бакалавра права. В 1617 Декарт поступает на службу в армию и много путешествует по Европе.
1619 год в научном отношении оказался ключевым для Декарта.
Именно в это время, как он сам писал в дневнике, ему открылись основания новой «удивительнейшей науки». Скорее всего, Декарт имел в виду открытие универсального научного метода, который он впоследствии плодотворно применял в самых разных дисциплинах.
В 1620-е годы Декарт знакомится с математиком М. Мерсенном, через которого он долгие годы «держал связь» со всем европейским научным сообществом.
В 1628 Декарт более чем на 15 лет обосновывается в Нидерландах, но не поселяется в каком-то одном месте, а около двух десятков раз меняет место жительства.
В 1633, узнав об осуждении церковью Галилея, Декарт отказывается от публикации натурфилософской работы «Мир», в которой излагались идеи естественного возникновения вселенной по механическим законам материи.
В 1637 на французском языке выходит работа Декарта «Рассуждение о методе», с которой, как многие считают, и началась новоевропейская философия.
Большое влияние на европейскую мысль оказала и последняя философская работа Декарта «Страсти души», опубликованная в 1649 г. В том же году по приглашению шведской королевы Кристины Декарт отправился в Швецию. Суровый климат и непривычный режим (королева заставляла Декарта вставать в 5 утра, чтобы давать ей уроки и выполнять другие поручения) подорвали здоровье Декарта, и, подхватив простуду, он
умер от пневмонии.
По традиции, введенной Декартом, «широта» точки обозначаются буквой x, «долгота» — буквой y
На этой системе основаны многие способы указания места.
Например, на билете в кинотеатр стоят два числа: ряд и место — их можно рассматривать как координаты места в зале.
Подобные координаты приняты в шахматах. Вместо одного из чисел берется буква: вертикальные ряды клеток обозначаются буквами латинского алфавита, а горизонтальные — цифрами. Таким образом, каждой клетке шахматной доски ставится в соответствие пара из буквы и числа, и шахматисты получают возможность записывать свои партии. О применении координат пишет в своём стихотворении «Сын артиллериста» Константин Симонов.
Всю ночь, шагая как маятник,
Глаз майор не смыкал,
Пока по радио утром
Донёсся первый сигнал:
«Всё в порядке, добрался,
Немцы левей меня,
Координаты (3;10),
Скорее давайте огня!
Орудия зарядили,
Майор рассчитал всё сам.
И с рёвом первые залпы
Ударили по горам.
И снова сигнал по радио:
«Немцы правей меня,
Координаты (5; 10),
Скорее ещё огня!
Летели земля и скалы,
Столбом поднимался дым.
Казалось, теперь оттуда
Никто не уйдёт живым.
Третий сигнал по радио:
«Немцы вокруг меня,
Координаты (4; 10),
Не жалейте огня.
Майор побледнел, услышав:
(4;10) — как раз
То место, где его Лёнька
Должен сидеть сейчас.
Константин Симонов «Сын артиллериста»
§2. Легенды об изобретении системы координат
Существует несколько легенд об изобретении системы координат, которая носит имя Декарта.
Легенда 1
До наших времён дошла такая история.
Посещая парижские театры, Декарт не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль, вызываемыми отсутствием элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.
Легенда2. Однажды РенеДекарт весь день пролежал в кровати, думая о чем-то, а муха жужжала вокруг и не давала ему сосредоточиться. Он стал размышлять, как бы описать положение мухи в любой момент времени математически, чтобы иметь возможность прихлопнуть ее без промаха. И…придумал, декартовы координаты, одно из величайших изобретений в истории человечества.
Марковцев Ю.
Однажды в незнакомый город
Приехал молодой Декарт.
Его ужасно мучил голод.
Стоял промозглый месяц март.
Решил к прохожей обратиться
Декарт, пытаясь, дрожь унять:
Где тут гостиница, скажите?
И дама стала объяснять:
– Идите до молочной лавки,
Потом до булочной, за ней
Цыганка продает булавки
И яд для крыс и для мышей,
А дальше будут магазины,
Найдете в них наверняка
Сыры, бисквиты, фрукты
И разноцветные шелка…
Все объяснения эти слушал
Декарт, от холода дрожа.
Ему хотелось очень кушать,
Но звонкий голос продолжал:
– За магазинами – аптека
(аптекарь там – усатый швед),
И церковь, где в начале века
Венчался, кажется, мой дед…
Когда на миг умолкла дама,
Вдруг произнес ее слуга:
– Идите три квартала прямо
И два направо. Вход с угла.
Это — третья небылица о случае, который подсказал Декарту идею координат.
Заключение
Создавая, свой проект мы узнали о применении координатной плоскости в различных областях науки и повседневной жизни, некоторые сведения из истории возникновения координатной плоскости и математиках сделавших большой вклад в это изобретение. Материал, который мы собрали в ходе написания работы, может быть использован на занятиях школьного кружка, в качестве дополнительного материала к урокам. Всё это может заинтересовать школьников и скрасить учебный процесс.
А закончить нам бы хотелось такими словами:
«Представь свою жизнь координатной плоскостью. Ось у — твое положение в обществе. Ось х — продвижение вперед, к цели, к твоей мечте. И как мы знаем, она бесконечна… мы можем падать вниз, все дальше углубляясь в минус, можем оставаться на нуле и ничего не делать, абсолютно ничего. Можем подниматься вверх, можем падать, можем идти вперед или возвращаться назад, а все из-за того, что вся наша жизнь это координатная плоскость и самое главное здесь, какая у тебя координата…»
Список используемой литературы
-
Глейзер Г.И. История математики в школе: — М.: Просвещение, 1981. – 239 с,, ил.
-
Ляткер Я. А. Декарт. М.: Мысль, 1975. – (Мыслители прошлого)
-
Матвиевская Г. П. Рене Декарт, 1596–1650. М.: Наука, 1976.
-
А. Савин. Координат. Квант. 1977. №9
-
Математика – приложение к газете «Первое сентября», №7, №20, №17, 2003г., №11, 2000г.
-
Зигель Ф.Ю. Звёздая азбука: Пособие для учащихся. – М.: Просвещение, 1981. – 191 с., ил
-
Стив Паркер, Николас Харрис. Иллюстрированная энциклопедия для детей. Тайны вселенной. Харьков Белгород. 2008
-
Материалы с сайта http://istina.rin.ru/
Просмотров работы: 2842
Руководитель:
Локоткова Оксана Анатольевна
В процессе работы над индивидуальным проектом по математике «Координаты в нашей жизни» учеником 6 класса школы была поставлена и реализована цель, выяснить, где еще кроме математики применяется система координат. Для этого автор дает определение понятиям «координаты» и «система «координат», кратко излагает историю возникновения системы координат.
Подробнее о проекте:
В ученической исследовательской работе по математике «Координаты в нашей жизни» автор рассматривает, в чем заключается основной принцип системы координат и выясняет, в каких областях и сферах нашей жизни не обойтись без системы координат. Также в работе изучено использование координатной плоскости в математике, и проанализирована роль географических координат.
В готовом творческом и исследовательском проекте по математике «Координаты в нашей жизни» автор выполняет практические задания, рассчитанные на построение изображений на координатной плоскости, а также изучает технологию расчета координатных данных для выполнения «рисунка» в прямоугольной системе координат. Предложенный детский проект позволяет научиться свободно ориентироваться на координатной плоскости и на географической карте.
Оглавление
Введение
1. Координаты. Системы координат.
1.1. История возникновения системы координат.
1.2. Координатная плоскость в математике.
1.3. Координаты вокруг нас.
1.4. Географические координаты.
2. Изображения на координатной плоскости.
2.1. Построение изображений на координатной плоскости.
2.2. Создание «рисунков» в прямоугольной системе координат.
Заключение
Приложение
Введение
С координатами в жизни мы сталкиваемся постоянно, можно сказать «на каждом шагу». Идея задавать положение точки на плоскости с помощью чисел зародилась в древности — прежде всего у астрономов и географов при составлении звездных и географических карт, календаря.
Подробное изучение координатной плоскости необходимо. Ведь координаты- это тот же адрес. В повседневной жизни в речи взрослых мы иногда слышим такую фразу: “Оставьте мне свои координаты”. Это выражение означает, что собеседник должен оставить свой адрес или номер телефона, что и считается в этом случае координатами человека. Главное здесь в том, что по этим данным можно найти человека.
Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта. Метод координат позволяет применять средства алгебры и математического анализа при решении геометрических задач. При работе с координатной плоскостью мы неоднократно можем менять расположение точек, размеры единичных отрезков, что требует высокого развития и логического мышления, и, следовательно, способствует его развитию.
В окружающем нас мире существует много явлений и объектов-прообразов, которые можно использовать для составления заданий на метод координат. Если на уроках математики, каждой точке на числовой прямой ставилась в соответствии единственная координата (единственный адрес), то на уроках географии каждой точке на карте соответствуют уже два адреса, две координаты – долгота и широта.
Например, координаты Кемерово: 37,60 восточной долготы и 55,80 северной широты. В математике встречается следующую запись: А (3; 5) – точке А сопоставлены в соответствие два числа, два адреса, две координаты. Так, значит, существует взаимосвязь между математическими координатами и географическими координатами. Весьма интересный материал предоставляет нам астрономия, где каждое созвездие тесно связанно с координатами.
Проблема: С координатами в геометрии мы сталкиваемся постоянно, а где еще применяется метод координат?
Цель: выяснить, где еще кроме математики применяется система координат.
Задачи:
- Познакомиться с историей возникновения системы координат.
- Научиться свободно ориентироваться на координатной плоскости и на географической карте.
- Научиться «рисовать» в прямоугольной системе координат.
История возникновения системы координат
История возникновения координат и системы координат начинается очень давно, первоначально идея метода координат возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи. Древнегреческого ученого Анаксимандра Милетского(610-546 до н. э.) считают составителем первой географической карты. Он четко описывал широту и долготу места, используя прямоугольные проекции. Более чем за 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.
Первоначальное применение координат конечно связано с астрономией и географией, с потребностью определять положение светил на небе и определенных пунктов на поверхности Земли, при составлении календаря, звездных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта. Основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту (см.приложение 1,рис.1).
До наших времён дошла такая история, которая подтолкнула его к открытию. Занимая в театре места, согласно купленным билетам, мы даже не подозреваем, кто и когда предложил ставший обычным в нашей жизни метод нумерации кресел по рядам и местам. Оказывается эта идея осенила знаменитого философа, математика и естествоиспытателя Рене Декарта (1596-1650)– того самого, чьим именем названы прямоугольные координаты.
Посещая парижские театры, он не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль, вызываемыми отсутствием элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.
Научное описание прямоугольной системы координат Рене Декарт впервые сделал в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Кроме того, в своей работе «Геометрия» (1637), открывшей взаимопроникновение алгебры и геометрии, Декарт ввел впервые понятия переменной величины и функции. «Геометрия» оказала огромное влияние на развитие математики. В декартовой системе координат получили реальное истолкование отрицательные числа.
Кроме математики интересы Декарта распространялись на физику, где он дал четкую формулировку закона инерции, открыл закон преломления световых лучей на границе двух различных сред («Диоптрика», 1637).
Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
Координатная плоскость в математике
Каждый объект имеет свой упорядоченный адрес (координаты). Таким образом, адрес или координаты – это числовое или буквенное обозначение того места, где находится объект.
Математиками была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале). Такая модель получила название координатная плоскость.
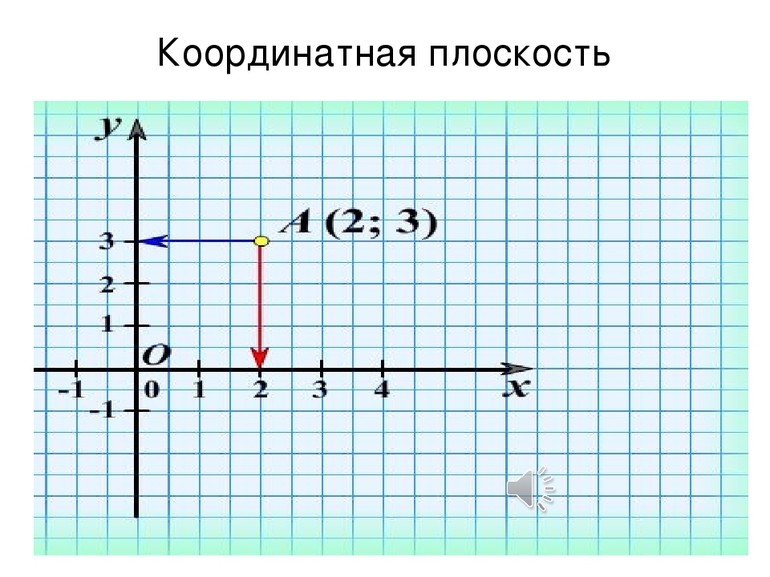
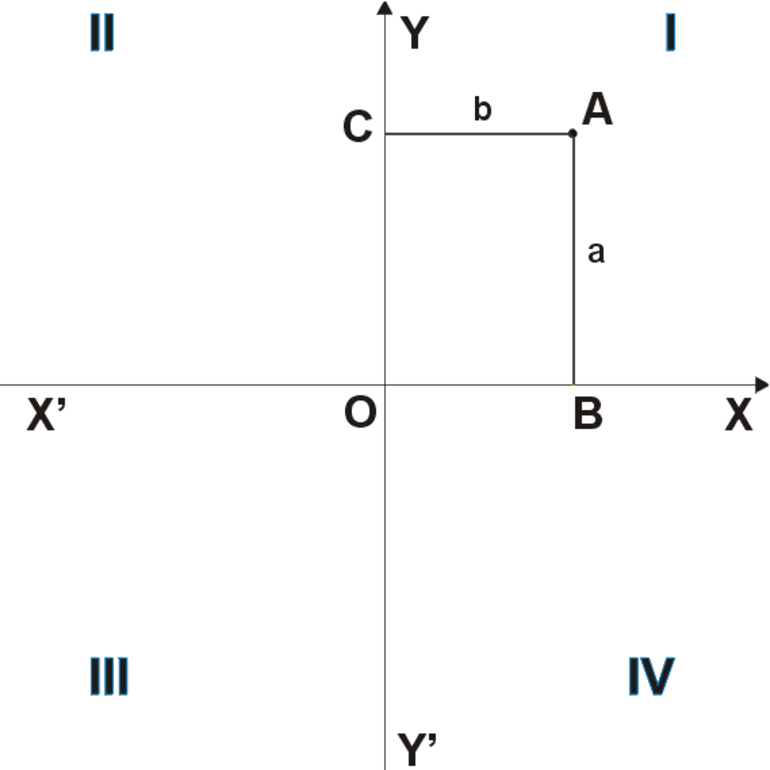
Чтобы из обычной плоскости получить координатную, необходимо начертить две перпендикулярные прямые, отмечая стрелками направления «вправо» и «вверх». На прямые наносят деления, как на линейку, причем точка пересечения прямых – это нулевая отметка для обеих шкал. Горизонтальную прямую обозначают Х и называют осью абсцисс, вертикальную прямую обозначают У и называют осью ординат.
Две перпендикулярные оси Х и У с разметкой называют прямоугольной, или декартовой, системой координат. Название «декартова» происходит от фамилии французского философа и математика Рене Декарта, который ее придумал (см.приложение 1,рис. 2).
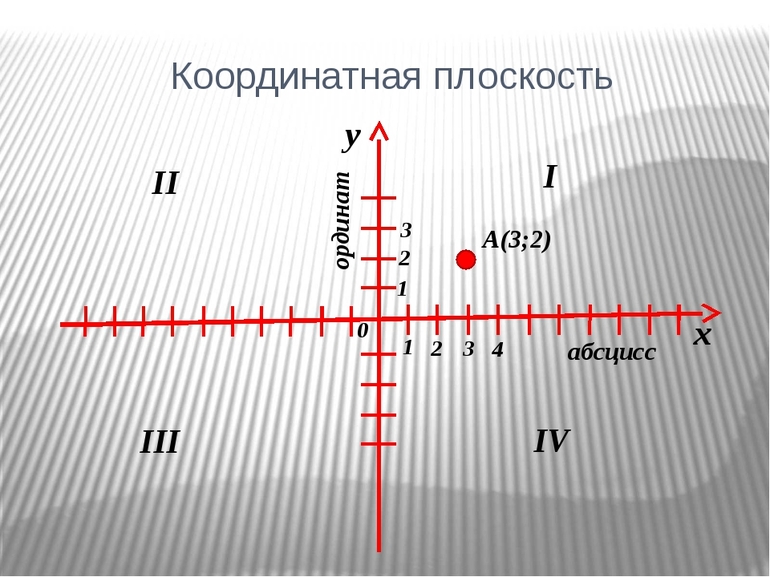
Для любой точки на координатной плоскости можно указать два числа (координаты). На рисунке показана точка на координатной плоскости. Для получения координат этой точки необходимо через точку провести две прямые, параллельные координатным осям (обозначены пунктирной линией). Пересечение одной из прямых с осью абсцисс – это координата точки, пересечение другой прямой с осью ординат – это координата точки. Сначала указывают координату, потом. Точка имеет координаты. Аналогично находим координаты точки, она имеет координаты.
Координаты вокруг нас
Системы координат пронизывают всю практическую жизнь человека. В нашей речи вы не раз могли слышать такую фразу: «Оставьте мне ваши координаты». Что означает это выражение? Догадались?! Собеседник просит записать свой адрес или номер телефона. У каждого человека бывают ситуации, когда необходимо определить местонахождение: по билету найдите место в зрительном зале или в вагоне поезда.
Координаты окружают нас повсюду:
- чтобы правильно занять свое место в кинотеатре нужно знать две координаты — ряд и место
- система географических координат (широта — параллели и долгота -меридианы)
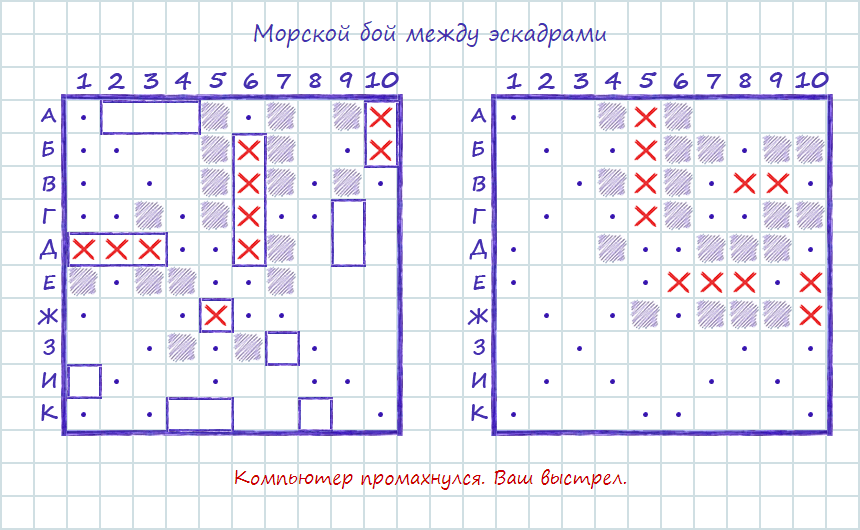
- те, кто в детстве играл в морской бой, тоже помнят, что каждая клетка на игровом поле определялась двумя координатами — буквой и цифрой
- с помощью координатной сетки летчики, моряки определяют местоположение объектов;
- в биологии — построение схем молекул ДНК, построение диаграмм и графиков, прослеживающих эволюцию развития
- в экономике — разнообразные системы координат применяются для построение графика спроса и предложения, при графическом изображении разных зависимых величин.
- в химии – построение таблицы Менделеева (изменение показателей происходит в горизонтальной и вертикальной плоскости)- взаимное расположение молекул.
- при астрономических наблюдениях координатная сетка накладывается на небесный свод с Землей в центре.
Географические координаты
Так же, как и каждый дом имеет свой адрес (с названием улицы, города), также и каждое место на поверхности Земли можно записать в виде адреса, используя линию широты (параллель) и линию долготы (меридиан), проходящие через это место. Чтобы найти некоторый объект в городе, в большинстве случаев достаточно знать его адрес. Трудности возникают, если нужно объяснить, где находится, например, дачный участок, место в лесу. Универсальным средством указания местоположения служат географические координаты.
При попадании в аварийную ситуацию, человек первым делом должен уметь ориентироваться на местности. Иногда необходимо определить географические координаты своего местоположения, например, чтобы передать спасательной службе или для других целей.
В современной навигации стандартно используется всемирная система координат WGS-84. В этой системе координат работают все GPS навигаторы и основные картографические проекты в Интернете. Координаты в системе WGS-84 столь же общеупотребимы и понятны всем, как всемирное время.
Местоположение любого объекта на поверхности Земли, его «адрес», определяется географической широтой («адрес» по горизонтали) и географической долготой («адрес» по вертикали). Широта и долгота — это географические координаты точки земной поверхности
Географическая широта. Параллели — это линии широты. Для всех точек одной и той же параллели широта одинакова. Начало отсчета широт — экватор, все точки которого имеют нулевую широту. От экватора широта отсчитывается в градусах вдоль меридиана до заданной точки. Все точки земной поверхности, находящиеся к северу от экватора, имеют северную широту (с. ш.); широта точек к югу от экватора — южная (ю. ш.). Следовательно, широта показывает, насколько далеко к северу или к югу от экватора расположен заданный пункт. Как северная, так и южная широта отсчитываются от 0 до 90° .
Географическая широта заданной точки определяется величиной в градусах дуги меридиана от экватора до параллели, проходящей у точку.
Географическая долгота. Долгота отсчитывается в градусах вдоль параллели. Началом отсчета долгот условно выбран Гринвичский (нулевой, начальный) меридиан, который проходит через старую Гринвичскую обсерваторию в Лондоне. Начальный меридиан и меридиан 180° разделяют Землю на Восточное и Западное полушария.
Все точки Восточного полушария имеют восточную долготу (в. д.), а Западного — западную долготу (з. д.). Как восточная, так и западная долгота отсчитываются от 0 до 180°. Цифры, обозначающие градусы долготы, написаны на глобусе и на карте полушарий у точек пересечения меридианов с экватором. Географическая долгота заданной точки определяется величиной в градусах дуги параллели от начального меридиана до меридиана, проходящего через эту точку.
Построение изображений на координатной плоскости
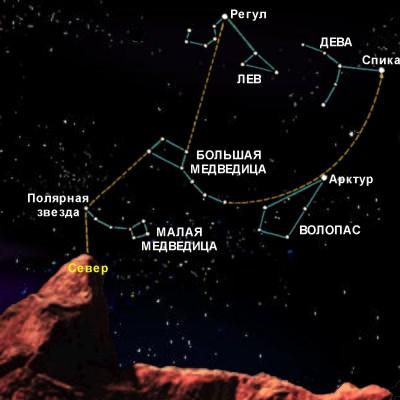
У древних греков существовала легенда о созвездиях Большой Медведицы и Малой Медведицы:«Всемогущий бог Зевс решил взять себе в жены прекрасную нимфу Калисто, одну из служанок богини Афродиты, вопреки желанию последней. Чтобы избавить Калисто от преследований богини, Зевс обратил Калисто в Большую Медведицу, а ее любимую собаку – в Малую Медведицу и взял их на небо».
Существует множество легенд и мифов о созвездиях. Фантазия древних греков поместила их на небо. Так появились созвездия Цефея, Андромеды, Персея и т.д. Знакомство с координатной плоскостью и вид звездного неба натолкнули на мысль, о переносе некоторых созвездий на координатную плоскость.
Созвездие Лев. В этом созвездии запечатлен Немейский Лев, над которым одержал победу Геракл.
Созвездие Близнецы. Созвездие названо в честь двух неразлучных братьев, сыновей Елены Прекрасной – Кастора и Полидевка..
Большая Медведица. Согласно греческому мифу это созвездие олицетворяет прекрасную нимфу Каллисто, превращенную Зевсом в Медведицу, чтобы спасти её от мести Геры.
Малая Медведица. Созвездие известно как Малый Ковш, последняя звезда в «ручке» которого – Полярная.
Орион. В греческой мифологии Орион – сын Посейдона и Эвриалы, великий охотник.
Телец. Созвездие названо в честь быка, на котором Европа переплыла море и попала к Зевсу на Крит.
Создание «рисунков» в прямоугольной системе координат
На координатной плоскости интересно строить рисунки, используя построение графов по координатам. Нужно сначала нарисовать рисунок, а затем его перенести на координатную плоскость, но при этом плавные соединения должны быть в виде отрезков.
Заключение
Таким образом, в результате проведения исследования, мной были решены поставленные задачи. А именно, я изучил координатную плоскость и связанные с ней понятия. Кроме того, мне удалось определить возможность создания графического изображения на координатной плоскости, то есть создать рисунок по известным координатам, а также перенести изображения созвездий с астрономической карты на координатную плоскость.
В результате проведения исследования я доказал, что координатная плоскость используется не только в математике, а пронизывает всю практическую жизнь человека.
В настоящее время координатный метод широко применяется в повседневной жизни. Современные системы спутниковой навигации позволяют определять координаты объекта, а также следить и управлять объектами, в том числе и движущимися. Эта тема также представляет сегодня большой интерес и может стать темой новой исследовательской разработки в будущем.
Приложение
Карточка № 1. Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(3;3); (0;3); (-3;2); (-5;2); (-7;4); (-8;3); (-7;1); (-8;-1);
(-7;-2); (-5;0); (-1;-2); (0;-4); (2;-4); (3;-2); (5;-2); (7;0); (5;2);
(3;3); (2;4); (-3;4); (-4;2); глаз (5;0).
Карточка № 2. Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(3;0); (1;2); (-1;2); (3;5); (1;7); (-3;6); (-5;7); (-3;4);
(-6;3); (-3;3); (-5;2); (-5;-2); (-2;-3); (-4;-4); (1;-4); (3;-3);
(6;1); (3;0); глаз (-1;5).
Карточка № 3. Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(1;7); (0;10); (-1;11); (-2;10); (0;7); (-2;5); (-7;3); (-8;0);
(-9;1); (-9;0); (-7;-2); (-2;-2); (-3;-1); (-4;-1); (-1;3); (0;-2);
(1;-2); (0;0); (0;3); (1;4); (2;4); (3;5); (2;6); (1;9); (0;10); глаз (1;6).
Карточка № 4. Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(1;-4); (1;-6); (-4;-6); (-3;-5); (-1;-5); (-3;-4); (-3;-3);
(-1;-1); (-1;0); (-3;0); (-3;-1); (-4;-1); (-4;0); (-3;1); (-1;1);
(-1;2); (-3;3); (-1;4); (0;6); (1;4); (1;2); (3;4); (6;5); (9;2); (9;0);
(9;-4); (6;-4); (5;-1); (4;-1); (1;-4); глаз (-1;3).
Ответы: 1 – утенок; 2 – заяц; 3 – белка; 4 – кошка.
Если страница Вам понравилась, поделитесь в социальных сетях:
Муниципальное общеобразовательное учреждение
«Новоивановская средняя общеобразовательная школа»
Свободненского района Амурской области
Координатная плоскость
Работу выполнили ученики 6 класса:
Гордеева Влада Алексеевна,
Чалая Анастасия Сергеевна
Руководитель работы Махун Вера Игнатьевна,
учитель математики
Новоивановка
2021 г.
Оглавление.
I. Введение……………………………………………………………………. .3
II. Основная часть………………………………………………………………..5
Координаты. Системы координат …………………………………………….. 5
2.1. История возникновения системы координат …………………………. .5
2.2. Координатная плоскость в математике ……………………………….. .6
2.3. Координаты вокруг нас…………………………………………………. 7
2.4. Географические координаты …………………………………………… 8
III. Изображения на координатной плоскости……………………………. .11
3.1. Построение изображений на координатной плоскости……………… 11
3.2. Создание «рисунков» в прямоугольной системе координат. ………. 12
IV. Выводы…………………………………………………………………… 13
V. Заключение ……………………………………………………………… ..13
VI. Библиографический список…………………………………………. … 14
VII. Приложение…………………………………………………………. …. 15
-
Введение.
С координатами в жизни мы сталкиваемся постоянно. Идея задавать положение точки на плоскости с помощью чисел зародилась в древности — прежде всего у астрономов и географов при составлении звездных и географических карт, календаря.
Подробное изучение координатной плоскости необходимо. Ведь координаты — это тот же адрес. В повседневной жизни в речи взрослых мы иногда слышим такую фразу: “Оставьте мне свои координаты”. Это выражение означает, что собеседник должен оставить свой адрес или номер телефона, что и считается в этом случае координатами человека. Главное здесь в том, что по этим данным можно найти человека. Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта. При работе с координатной плоскостью мы неоднократно можем менять расположение точек, размеры единичных отрезков, что требует высокого развития и логического мышления, и, следовательно, способствует его развитию. В окружающем нас мире существует много явлений и объектов-прообразов, которые можно использовать для составления заданий на метод координат. Если на уроках математики, каждой точке на числовой прямой ставилась в соответствии единственная координата (единственный адрес), то на уроках географии каждой точке на карте соответствуют уже два адреса, две координаты – долгота и широта. В математике встречается следующую запись: А (3; 5) – точке А сопоставлены в соответствие два числа, два адреса, две координаты. Так, значит, существует взаимосвязь между математическими координатами и географическими координатами. Весьма интересный материал предоставляет нам астрономия, где каждое созвездие тесно связанно с координатами.
Проблема: С координатами в математике мы сталкиваемся постоянно, а где еще применяется метод координат?
Цель: выяснить, где еще кроме математики применяется система координат.
Задачи:
-
Познакомиться с историей возникновения системы координат.
-
Научиться свободно ориентироваться на координатной плоскости и на географической карте.
-
Построить некоторые изображения созвездий на координатной плоскости.
-
Научиться «рисовать» в прямоугольной системе координат.
Гипотеза: Если термин «координатная плоскость» математический, то он используется только в математике/
Методы исследования:
-
Изучение интернет ресурсов и литературы.
-
Нахождение координат в жизни человека.
-
Поиск и построение изображений на координатной плоскости.
-
Самостоятельное построение фигур.
Предмет исследования: координатная плоскость.
Объект исследования: координатная плоскость, географические координаты.
II. Основная часть.
2.1. История возникновения системы координат
История возникновения координат и системы координат начинается очень давно, первоначально идея метода координат возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи. Древнегреческого ученого Анаксимандра Милетского (610-546 до н. э.) считают составителем первой географической карты. Он четко описывал широту и долготу места, используя прямоугольные проекции. Более чем за 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.
Первоначальное применение координат конечно связано с астрономией и географией, с потребностью определять положение светил на небе и определенных пунктов на поверхности Земли, при составлении календаря, звездных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта. Основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту. (Приложение 1).
До наших времён дошла такая история, которая подтолкнула его к открытию. При посещении театра, мы занимаем в театре места, согласно купленным билетам, мы даже не подозреваем, кто и когда предложил ставший обычным в нашей жизни метод нумерации кресел по рядам и местам. Оказывается, эта идея осенила знаменитого философа, математика и естествоиспытателя Рене Декарта (1596-1650)– того самого, чьим именем названы прямоугольные координаты.
Посещая парижские театры, он не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль, вызываемыми отсутствием элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.
Научное описание прямоугольной системы координат Рене Декарт впервые сделал в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Кроме того, в своей работе «Геометрия» (1637), открывшей взаимопроникновение алгебры и геометрии, Декарт ввел впервые понятия переменной величины и функции. «Геометрия» оказала огромное влияние на развитие математики. В декартовой системе координат получили реальное истолкование отрицательные числа.
Кроме математики интересы Декарта распространялись на физику, где он дал четкую формулировку закона инерции, открыл закон преломления световых лучей на границе двух различных сред («Диоптрика», 1637).
Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
2.2. Координатная плоскость в математике
Каждый объект имеет свой упорядоченный адрес (координаты). Таким образом, адрес или координаты – это числовое или буквенное обозначение того места, где находится объект.
Математиками была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале). Такая модель получила название координатная плоскость.
Чтобы из обычной плоскости получить координатную, необходимо начертить две перпендикулярные прямые, отмечая стрелками направления «вправо» и «вверх». На прямые наносят деления, как на линейку, причем точка пересечения прямых – это нулевая отметка для обеих шкал. Горизонтальную прямую обозначают х и называют осью абсцисс, вертикальную прямую обозначают у и называют осью ординат. Две перпендикулярные оси х и у с разметкой называют прямоугольной, или декартовой, системой координат. Название «декартова» происходит от фамилии французского философа и математика Рене Декарта, который ее придумал (Приложение 1).
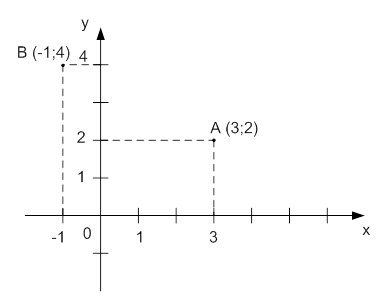
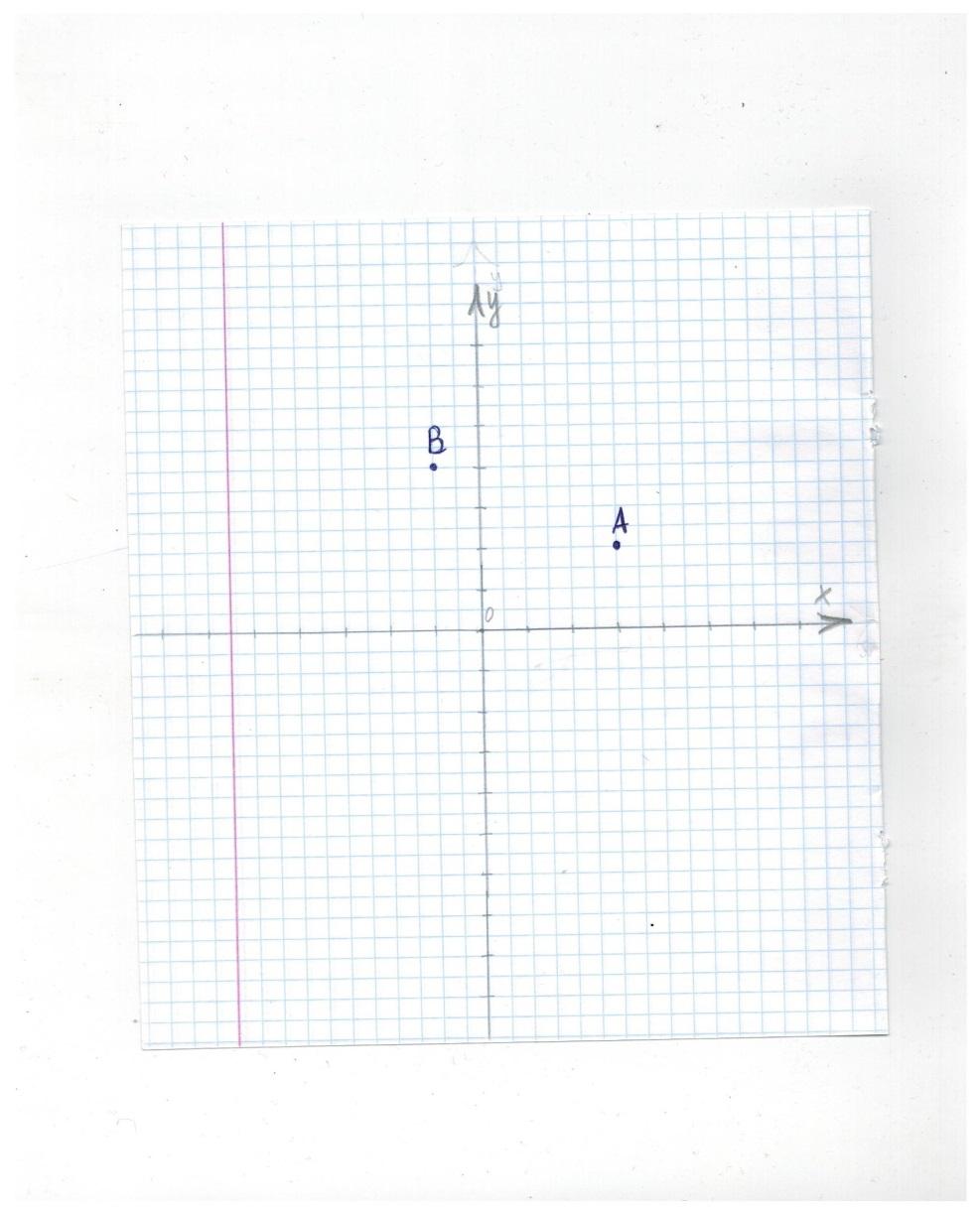
Для любой точки на координатной плоскости можно указать два числа (координаты). На рисунке показана точка А на координатной плоскости. Для получения координат этой точки необходимо через точку провести две прямые, параллельные координатным осям (обозначены пунктирной линией). Пересечение одной из прямых с осью абсцисс – это координата х точки А, пересечение другой прямой с осью ординат – это координата у точки А. Сначала указывают координату х, потом у. Точка А имеет координаты (3;2) . Аналогично находим координаты точки В, она имеет координаты (-1; 4) (Приложение 1).
2.3. Координаты вокруг нас
Системы координат пронизывают всю практическую жизнь человека. Координаты окружают нас повсюду:
-
если умеете играть в шашки и шахматы, знает, что вертикальные полосы обозначаются цифрами, а горизонтальные – буквами (Приложение 1),
-
архитекторы используют систему координат в своих расчётах по проектированию строительных объектов (Приложение 1),
-
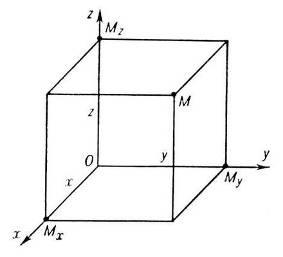
геометрия одна из наук, которая наиболее ярким способом использует систему координат (Приложение 1),
-
в географии система координат географических координат используется достаточно давно, широта — параллели и долгота – меридианы — оси декартовой системы координат (Приложение 1),
-
чтобы правильно занять свое место в кинотеатре нужно знать две координаты — ряд и место (Приложение1),
-
те, кто играл в морской бой, знает, что каждая клеточка на игровом поле определяется двумя координатами — буквой и цифрой (Приложение 1),
-
с помощью координатной сетки летчики, моряки определяют местоположение объектов;
-
в биологии — построение схем молекул ДНК, построение диаграмм и графиков, прослеживающих эволюцию развития
-
в экономике — разнообразные системы координат применяются для построения графика спроса и предложения, при графическом изображении разных зависимых величин.
-
в химии – построение таблицы Менделеева (изменение показателей происходит в горизонтальной и вертикальной плоскости)- взаимное расположение молекул,
-
с помощью системы координат, астрономы определяют расстояние до звёзд, их месторасположение на карте звёздного неба, размеры галактики, скорость её вращения, траекторию движения планет и их размеры.
2.4. Географические координаты
Так же, как и каждый дом имеет свой адрес (с названием улицы, города), также и каждое место на поверхности Земли можно записать в виде адреса, используя линию широты (параллель) и линию долготы (меридиан), проходящие через это место. Чтобы найти некоторый объект в городе, в большинстве случаев достаточно знать его адрес. Трудности возникают, если нужно объяснить, где находится, например, дачный участок, место в лесу. Универсальным средством указания местоположения служат географические координаты.
При попадании в аварийную ситуацию, человек первым делом должен уметь ориентироваться на местности. Иногда необходимо определить географические координаты своего местоположения, например, чтобы передать спасательной службе или для других целей.
Местоположение любого объекта на поверхности Земли, его «адрес», определяется географической широтой («адрес» по горизонтали) и географической долготой («адрес» по вертикали). Широта и долгота — это географические координаты точки земной поверхности
Например, координаты нашего села Новоивановка: 1270 59/ восточной долготы и 510 24/ северной широты.
Географическая широта. Параллели — это линии широты. Для всех точек одной и той же параллели широта одинакова. Начало отсчета широт — экватор, все точки которого имеют нулевую широту. От экватора широта отсчитывается в градусах вдоль меридиана до заданной точки. Все точки земной поверхности, находящиеся к северу от экватора, имеют северную широту (с. ш.); широта точек к югу от экватора — южная (ю. ш.). Следовательно, широта показывает, насколько далеко к северу или к югу от экватора расположен заданный пункт. Как северная, так и южная широта отсчитываются от 0 до 90°.
Географическая широта заданной точки определяется величиной в градусах дуги меридиана от экватора до параллели, проходящей у точки.
Географическая долгота. Долгота отсчитывается в градусах вдоль параллели. Началом отсчета долгот условно выбран Гринвичский (нулевой, начальный) меридиан, который проходит через старую Гринвичскую обсерваторию в Лондоне. Начальный меридиан и меридиан 180° разделяют Землю на Восточное и Западное полушария. Все точки Восточного полушария имеют восточную долготу (в. д.), а Западного — западную долготу (з. д.). Как восточная, так и западная долгота отсчитываются от 0 до 180°. Цифры, обозначающие градусы долготы, написаны на глобусе и на карте полушарий у точек пересечения меридианов с экватором. Географическая долгота заданной точки определяется величиной в градусах дуги параллели от начального меридиана до меридиана, проходящего через эту точку.
III. Изображения на координатной плоскости
3.1. Построение изображений на координатной плоскости.
Все еще с детства любят рассматривать звезды на небе. Нам всегда нравилось наблюдать за звездным небом. Когда мы наблюдали за этими звездами, мы поняли, что они расположены определенным образом.
О зодиакальных созвездиях знают многие, но находить их смогут не все. Эта работа направлена на построение знаков Зодиака на координатной плоскости. Мы построили в системе координат некоторые созвездия.
Астрология — наука о влиянии звезд, созвездий и планет на человека и на Землю. Среди 88 созвездий, украшающих ночное небо, особое место занимают те, среди которых Солнце проходит свой годичный путь. Двенадцать созвездий на пути у Солнца: Овен, Телец, Близнецы, Рак, Лев, Дева, Весы, Скорпион, Стрелец, Козерог, Водолей, Рыбы. Большинство имён принадлежит животным, поэтому эти созвездия получили названия зодиакальные (от греческого зодиакос — «звериный круг»).
На самом деле, конечно, Земля движется вокруг своего светила, но нам кажется, что именно Солнце меняет своё местоположение. Так думали и древние астрономы, давшие названия зодиакальным созвездиям.
Перенесём на координатную плоскость созвездия.
Созвездие “Овен” (-5;5), (-1;3), (0;6), (0;2).
Созвездие «Близнецы» (-5;5), (-2;5), (-1;8), (3;2), (6;1), (5;-1), (-7;3), (-5;2), (-5;1), (-2;2), (3;-2), (5;-3), (-1;5), (4;-5).
Созвездие “ Рак” (0;7), (0;3), (2;2), (2;0), (0;0), (-2;-2), (-3;-4), (4;-5).
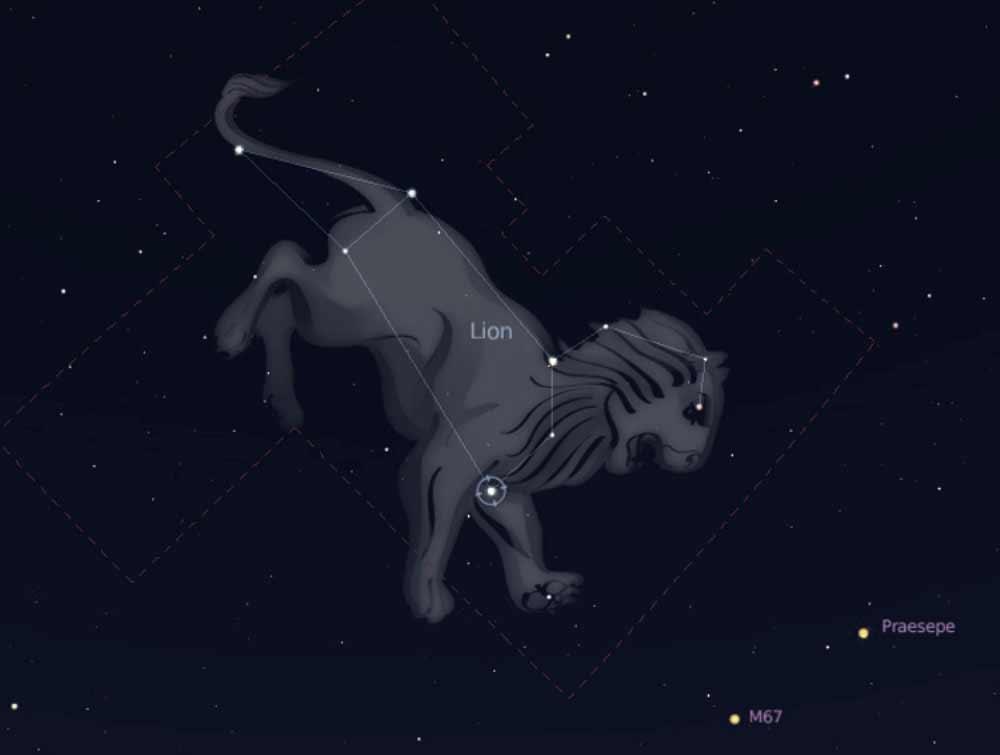
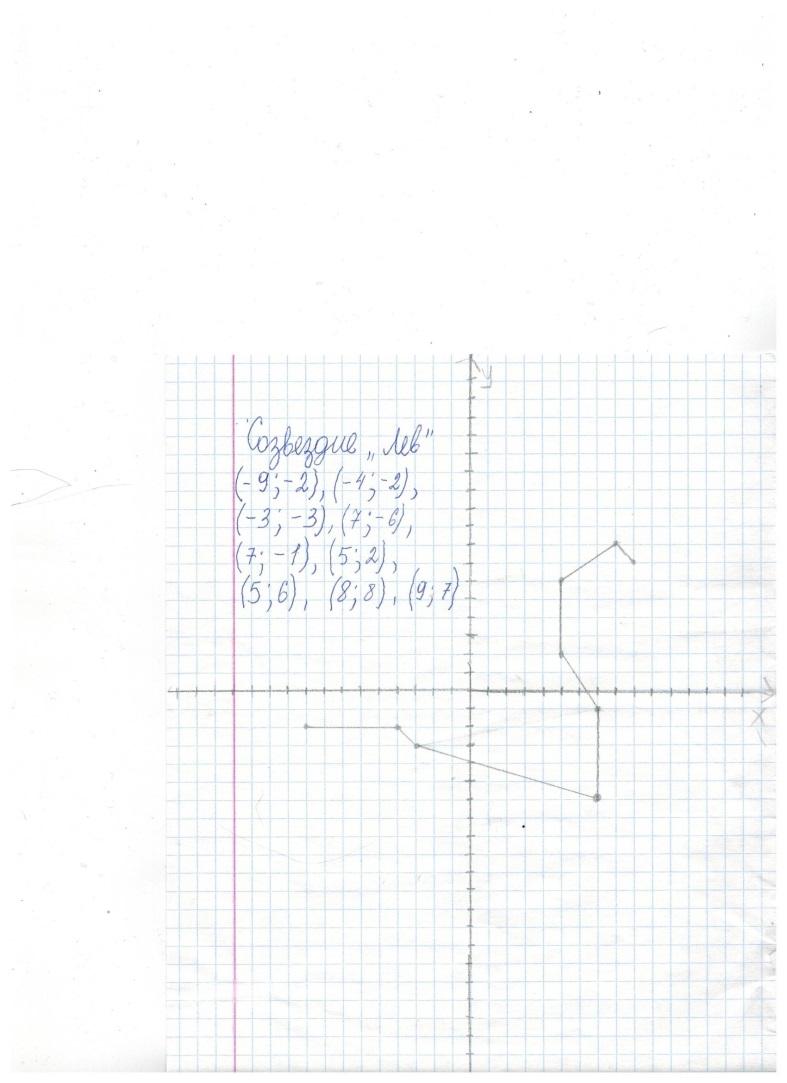
Созвездие “Лев” (-9;-2), (-4;-2), (-3;-3), (7;-6), (7;-1), (5;2), (5;6), (8;8),(9;7).
Созвездие “ Дева” (1;9), (5;8), (1;5), (-1;-1), (6;1), (-8;3), (-7;-3), (-4;-3), (-1;-5), (0;-2), (2;1).
Созвездие “Весы” (-1;4), (-6;-1), (7;-1), (2;-5), (-1;4).
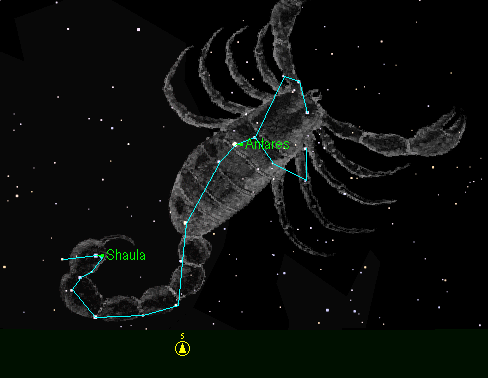
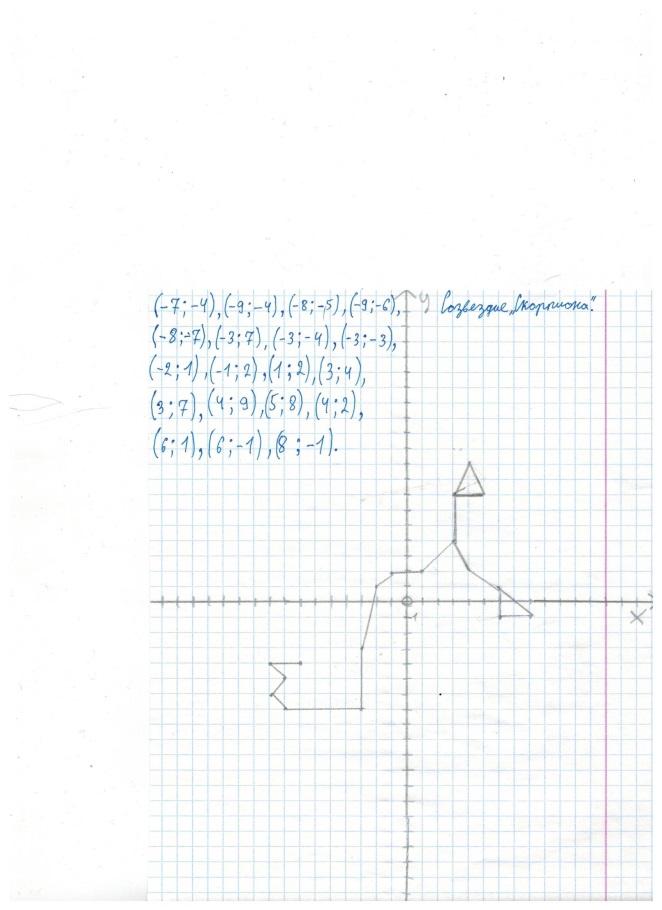
Созвездие «Скорпион» (-7;-4),(-9;-4),(-8;-5),(-9;-6),(-8;-7),(-3;-7),(-3;-4), (-3;-3), (-2;1), (-1;2), (1;2), (3;4), (3;7), (4;9), (5;8), (4;2), (6;1), (6;-1), (8;-1).
Созвездие «Стрелец» (2;6), (-1;2), (-3;1), (-4;2), (-6;1), (-5;2), (1;-1), (3;-1), (0;-4), (1;-6).
Созвездие «Козерог» (8;9), (0;3), (-5;6), (-9;7), (-7;1), (-4;-4), (-2;-6), (1;-8), (3;-6), (7;5).
Созвездие “ Водолей” (-3;-9), (-6;7), (-4;6), (-3;5), (-7;2), (-7;-3), (-7;-5), (-9;-8), (-1;6), (3;2), (8;-2).
Созвездие «Рыбы» (-1;7), (-2;6), (-3;4), (-5;0), (-6;-2), (-9;-9), (-8;-8), (-7;-7),
(-3;-5), (-1;-5), (1;-6), (5;-4), (6;-6), (8;-6), (9;-7), (8;-8), (6;-8).
Мы нарисовали в системе координат созвездия: «Весы», «Скорпион», «Рыбы», «Козерог».
3.2 Создание «рисунков» в прямоугольной системе координат.
На координатной плоскости интересно строить рисунки. Нужно сначала нарисовать рисунок, а затем его перенести на координатную плоскость, но при этом плавные соединения должны быть в виде отрезков. Упоминание о координатах можно увидеть в стихотворении К. Симонова «Сын артиллериста», где говорится о молодом воспитаннике пожилого майора – Лёньке, который корректировал по радио огонь артиллерийской батареи.
«Третий сигнал по радио:
Немцы вокруг меня,
Бейте четыре – десять,
Не жалейте огня!»
Майор побледнел, услышав,
Четыре – десять – как раз
То место, где Лёнька
Должен сидеть сейчас.
IV. Выводы:
-
Координатная плоскость используется не только в математике.
-
Мы научились свободно ориентироваться на координатной плоскости, и на географической карте, теперь можем свободно помогать своим одноклассникам.
-
Изучили много источников информации, в которой представлен материал о координатной плоскости, географических координатах.
-
Убедились, что координаты окружают нас повсюду.
V. Заключение.
Таким образом, в результате проведения исследования, мы решили поставленные задачи. А именно, мы изучили координатную плоскость и связанные с ней понятия. Кроме того, нам удалось определить возможность создания графического изображения на координатной плоскости, то есть создать рисунок по известным координатам, а также перенести изображения созвездий с астрономической карты на координатную плоскость.
В результате проведения исследования выдвинутая гипотеза не получила подтверждение. Мы доказали, что координатная плоскость используется не только в математике, а пронизывает всю практическую жизнь человека; исследовали знаки зодиака через теорию координатной плоскости.
В настоящее время координатный метод широко применяется в повседневной жизни. Современные системы спутниковой навигации позволяют определять координаты объекта, а также следить и управлять объектами, в том числе и движущимися. Эта тема также представляет сегодня большой интерес и может стать темой новой исследовательской разработки в будущем.
V. Библиографический список.
-
Математика. 6 класс: Учебник для учащихся общеобразовательных Учреждений / Мерзляк А.Г., Полонский В.Б., Якир М.С. /под ред. Подольского В.Е. ООО «Издательский центр Вентана – Граф, 2018.
-
И.И.Зубарева, А.Г.Мордкович Математика 6 класс. —
М. :Мнемозина,2010
-
Коваленко В.Г. Дидактические игры на уроках математики: Кн. для учителя. — М.: Просвещение, 1990.-96 с.
-
Горячкина О. Координатная плоскость// Математика.-1995-№47.-с.8.
-
Рисуем по координатам//Математика. 2000. №46.47. с.12,22.
-
Красивые задания по теме “Координатная плоскость”// Математика. 1997. №38
-
https://ru.wikipedia.org/wiki/Морской_бой_(игра)
-
https://ru.wikipedia.org/wiki/Геометрия_(Декарт)
Приложение 1.







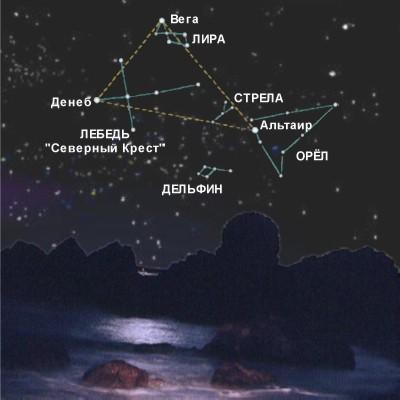
Созвездие «Весы»
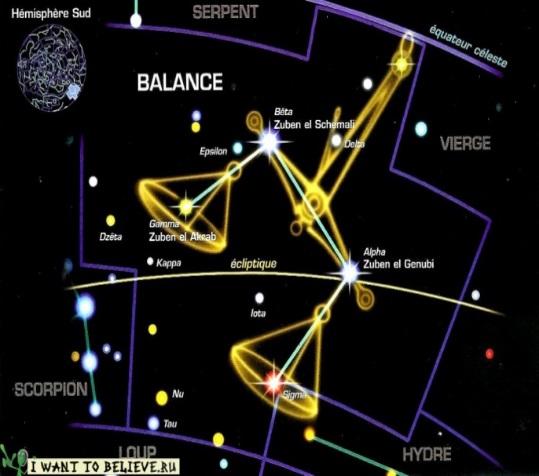
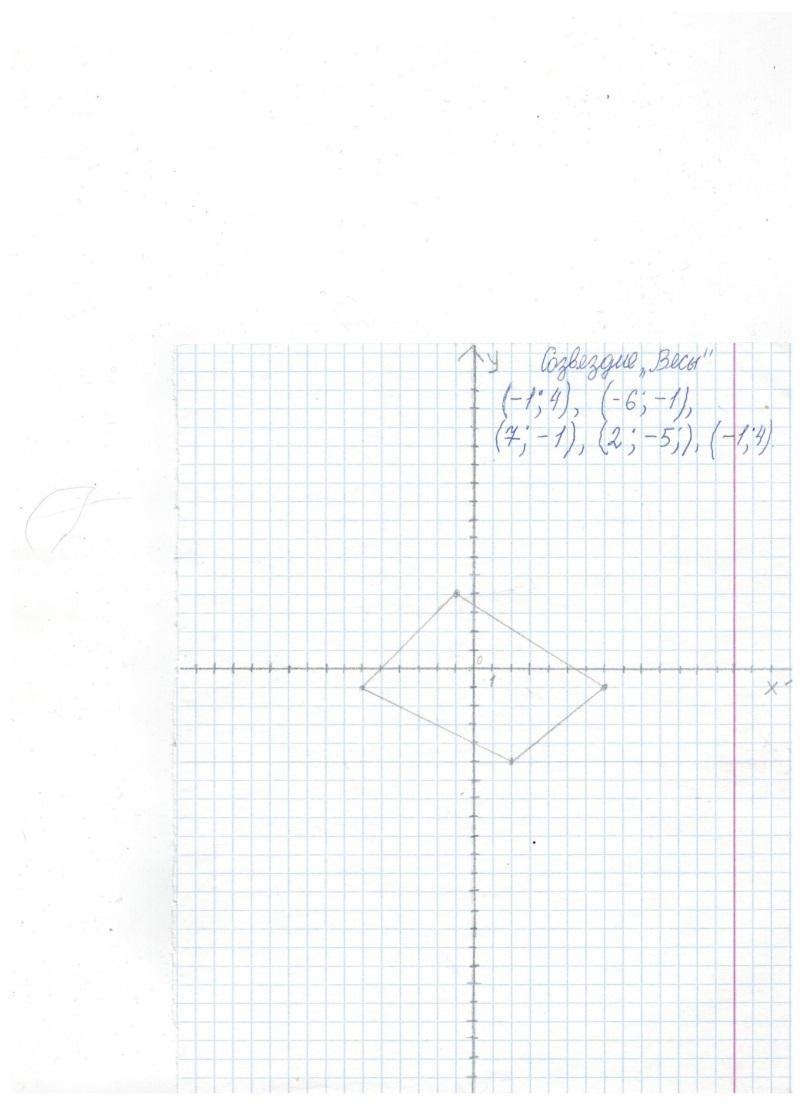
Созвездие «Рыбы»

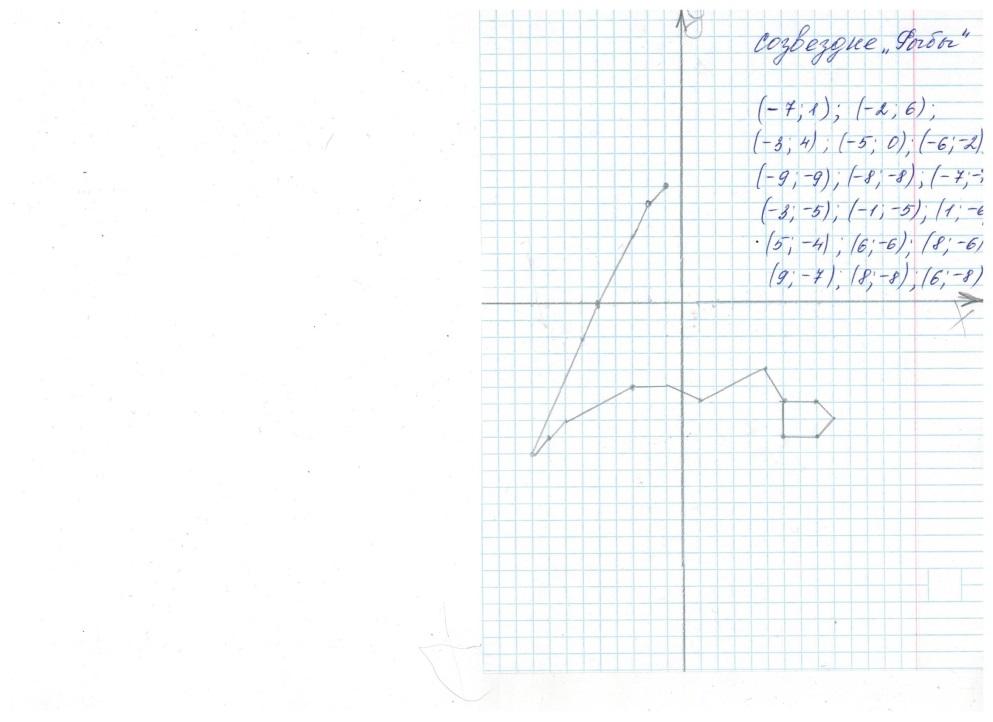
Созвездие «Скорпион»
Созвездие «Лев»
. 
Созвездие «Козерог»
Приложение 2
Уточка.
(-1; 2); (3; 5); (1; 8); (-3; 7); (-5; 8); (-3; 4); (-6; 3); (-3; 3); (-5; 2); (-5; -2); (-2; -3); (-4; -4); (1; -4); (3; -3); (6; 1); (3; 0); (1; 2); (-1; 2) Глаз (-1; 5)
«Медведь»
(4; -4); (4; -6); (8,5; — 7,5); (9; — 7); (9; — 6); (9,5; — 5); (9,5; — 3,5); (10; — 3);
(10,5; — 2,5); (4; 5); (3; 6); (2; 6); (0; 5); (-3; 5); (-7; 3); (-9; — 1); (-8; -5); (-8; -7);
(-4,5; — 8); (-4,5; — 7); (-5; — 6,5); (-5; — 6); (-7,5; -5); (-4; -5); (-4; -7); (-1; -7);
(1; -6); (-2; -6); (1; -4); (3; -8); (3; -7); (2; -7); (2; -6); (3; -5); (3; -6); (5; -7); (7; -7)
Ухо: (6; -4); (6; -3); (7; -2,5); (7,5; -3)
Глаз: (8; -6).
«Мухомор»
Собачка
(-1; 7); (-1; 6); (0; 4); (0; 3); (-1; 2); (-4; 2); (-5; 3); (-5; 4); ( -4; 6); (-4; 7); (-6; 5); (-6; 4); (-7; 3); (-7; 2); (-6; 1); (-5; 1); (-4; 0); (-3; -3); (-4; -5); (-5; -4); (-6; -4); (-7; -5); (-6; -6); (-3; -6); (-1; 5); (0; -3); (2; -2); (3; -3); (4; -3); (5; -4); (5; -5); (4; -5); (3; -4); (2; -4); (1; -5); (2; -6); (7; -6); (10; -2); (12; -2); (12; 0); (10; 0); (10; -1); (8; 1); (6; 2); (4; 2); (0,5); (-1; 7); (-4; 7)
18
Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию.
Я.А. Каменский
Цели:
- Закрепить навык нахождения координат точек и построения точек по их координатам;
- Показать практическое значение координатной плоскости в жизни человека;
- Научить обрабатывать и обобщать полученную в результате исследования информацию;
- Формировать навыки работы в сфере самостоятельной познавательной деятельности; воспитывать ответственность за порученное дело;
- Воспитывать внимательность, аккуратность при выполнении построений.
Ход урока
I. Мотивационный материал
Однажды в незнакомый город
Приехал молодой Декарт.
Его ужасно мучил голод.
Стоял промозглый месяц март.
Решил к прохожей обратиться
Декарт, пытаясь, дрожь унять:
Где тут гостиница, скажите?
И дама стала объяснять:
– Идите до молочной лавки,
Потом до булочной, за ней
Цыганка продает булавки
И яд для крыс и для мышей,
А дальше будут магазины,
Найдете в них наверняка
Сыры, бисквиты, фрукты
И разноцветные шелка…
Все объяснения эти слушал
Декарт, от холода дрожа.
Ему хотелось очень кушать,
Но звонкий голос продолжал:
– За магазинами – аптека
(аптекарь там – усатый швед),
И церковь, где в начале века
Венчался, кажется, мой дед…
Когда на миг умолкла дама,
Вдруг произнес ее слуга:
– Идите три квартала прямо
И два направо. Вход с угла.
Я вам рассказала небылицу о случае, который подсказал Декарту идею координат. И сегодня мы с вами узнаем о применении координатной плоскости в различных областях науки и профессиях, некоторые сведения из истории возникновения координатной плоскости и математиках сделавших большой вклад в это изобретение.
На нашем уроке присутствуют литератор, историк, библиограф, астроном.
II. Проверка домашнего задания.
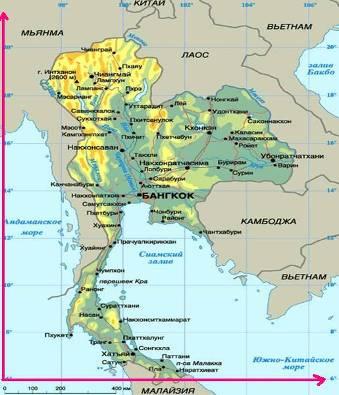
а) Определить по карте координаты городов: Москва (56° с.ш., 38° в.д.), Хабаровск (480 с.ш., 1350 в.д.), Владивосток (430 с.ш., 1320 в.д.), Уссурийск (44° с.ш. 132° в.д.) и показать на физической карте их расположение.
б) Своеобразные координаты используют в шахматах, где положение фигуры на доске определяется с помощью буквы и числа. Вертикальные ряды обозначаются буквами латинского алфавита, горизонтальные – цифрами. Применение координат в шахматах позволяет играть в шахматы по переписке. Чтобы сообщить ход, нет надобности, рисовать доску и расположение фигур. Достаточно, например, сказать: «Гроссмейстер сыграл е2 – е4, и всем уже известно, как начата партия.
в) Общаясь друг с другом, люди часто говорят: «Оставьте свои координаты». Для чего?…Чтобы человека было легко найти. Это могут быть: номер телефона, домашний адрес, место работы, Email. Суть координат или системы координат состоит в том, что это правило, по которому определяется положение объекта.
Мы с вами видим, чтобы найти положение города или другого предмета на плоскости необходимо знать его координаты. Об этом говорится и в стихотворении Константина Симонова Сын артиллериста.
III. Предоставляем слово литератору.
Он познакомит с отрывком из этого стихотворения, которое хорошо вам известно из уроков литературы.
Всю ночь, шагая как маятник,
Глаз майор не смыкал,
Пока по радио утром
Донёсся первый сигнал:
Всё в порядке, добрался,
Немцы левей меня,
Координаты (3;10),
Скорее давайте огня!
Орудия зарядили,
Майор рассчитал всё сам.
И с рёвом первые залпы
Ударили по горам.
И снова сигнал по радио:
Немцы правей меня,
Координаты (5; 10),
Скорее ещё огня!
Летели земля и скалы,
Столбом поднимался дым.
Казалось, теперь оттуда
Никто не уйдёт живым.
Третий сигнал по радио:
Немцы вокруг меня,
Координаты (4; 10),
Не жалейте огня.
Майор побледнел, услышав:
(4;10) – как раз
То место, где его Лёнька
Должен сидеть сейчас.
А можно ли по одной координате точно определить положение точки на плоскости? Трудно, а иногда и невозможно.
Послушайте о чём говорилось в найденной записке в романе Жюля Верна «Дети капитана Гранта”, а все произошло из-за записки: “7 июня 1862 года трёхмачтовое судно “Британия” Глазго потерпело крушение …гони…южн…берег …два матроса…пл. Капитан Гр… дости…контин… пл. …жесток…инд…брошен этот документ …долготы и 37°11 широты …окажите им помощь … погибнут.”
Вывод:
Точное положение точки на плоскости определяют две координаты.
Для точного определения положения точки на плоскости нужно иметь координатную плоскость.
Историк познакомит вас с возникновением понятия координатная плоскость.
Предоставим ему слово.
История возникновения координат и системы координат начинается очень неожиданно, первоначально идея метода координат возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи. Древнегреческого ученого Анаксимандра Милетского (ок. 610-546 до н. э.) считают составителем первой географической карты. Он четко описывал широту и долготу места, используя прямоугольные проекции. Более чем за 100 лет до нашей эры греческий учёный Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести хорошо теперь известные географические координаты: широту и долготу и обозначать их числами. Уже во II веке греческий астроном Клавдий Птолемей пользовался широтой и долготой в качестве координат. Прямоугольной сеткой пользовались также художники эпохи Возрождения.
В XIV веке французский математик Оресм ввёл, по аналогии с географическими, координаты на плоскости. Он предложил покрыть плоскость прямоугольной сеткой и называть широтой и долготой то, что мы теперь называем абсциссой и ординатой. Это нововведение оказалось очень продуктивным. На его основе возник метод координат, связавший геометрию с алгеброй. Точка плоскости заменяется парой чисел (х; у), т.е. алгебраическим объектом.
Основная заслуга в создании метода координат принадлежит французскому математику Рене Декарту.
Предоставим слово библиографу.
Гениальный французский ученый и мыслитель XVII века Рене Декарт (1596–1650)далеко не сразу нашел свое место в жизни. Родившись в дворянской семье, Декарт получил хорошее образование. В 1606 году отец отправил его в иезуитскую коллегию Ла Флеш. Учитывая не очень крепкое здоровье Декарта, ему делали некоторые послабления в строгом режиме этого учебного заведения, например, разрешали вставать позже других. Приобретя в коллегии немало познаний, Декарт в то же время проникся антипатией к схоластической философии, которую он сохранил на всю свою жизнь.
После окончания коллегии Декарт продолжил образование. В 1616 в университете Пуатье он получил степень бакалавра права. В 1617 Декарт поступает на службу в армию и много путешествует по Европе.
1619 год в научном отношении оказался ключевым для Декарта. Именно в это время, как он сам писал в дневнике, ему открылись основания новой «удивительнейшей науки». Скорее всего, Декарт имел в виду открытие универсального научного метода, который он впоследствии плодотворно применял в самых разных дисциплинах.
В 1620-е годы Декарт знакомится с математиком М. Мерсенном, через которого он долгие годы «держал связь» со всем европейским научным сообществом.
В 1628 Декарт более чем на 15 лет обосновывается в Нидерландах, но не поселяется в каком-то одном месте, а около двух десятков раз меняет место жительства.
В 1633, узнав об осуждении церковью Галилея, Декарт отказывается от публикации натурфилософской работы «Мир», в которой излагались идеи естественного возникновения вселенной по механическим законам материи.
В 1637 на французском языке выходит работа Декарта «Рассуждение о методе», с которой, как многие считают, и началась новоевропейская философия.
Большое влияние на европейскую мысль оказала и последняя философская работа Декарта «Страсти души», опубликованная в 1649 г. В том же году по приглашению шведской королевы Кристины Декарт отправился в Швецию. Суровый климат и непривычный режим (королева заставляла Декарта вставать в 5 утра, чтобы давать ей уроки и выполнять другие поручения) подорвали здоровье Декарта, и, подхватив простуду, он у мер от пневмонии.
Существует несколько легенд об изобретении системы координат, которая носит имя Декарта.
До наших времён дошла такая история.
Посещая парижские театры, Декарт не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль, вызываемыми отсутствием элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.
Легенда 2.
Однажды Рене Декарт весь день пролежал в кровати, думая о чем-то, а муха жужжала вокруг и не давала ему сосредоточиться. Он стал размышлять, как бы описать положение мухи в любой момент времени математически, чтобы иметь возможность прихлопнуть ее без промаха. И … придумал, декартовы координаты, одно из величайших изобретений в истории человечества.
Мы отправляемся в звездную обсерваторию и предоставляем слово астроному.
Легенда 1.
У древних греков существовала легенда о созвездиях Большой и Малой Медведиц. Всемогущий бог Зевс решил взять себе в жены прекрасную нимфу Калисто, одну из служанок богини Афродиты, вопреки желанию последней. Чтобы избавить Калисто от преследований богини, Зевс обратил Калисто в Большую Медведицу, ее любимую собаку – в Малую Медведицу и взял их на небо.
Легенда 2
В незапамятные времена у царя эфиопов Цефея была красавица-жена – царица Кассиопея. Однажды Кассиопея имела неосторожность похвастать своей красотой в присутствии нереид – жительниц моря. Обидевшись, завистливые нереиды пожаловались богу моря Посейдону, и он напустил на берега Эфиопии страшное чудовище – Кита.
Чтобы откупиться от Кита, опустошавшего страну, Цефей вынужден был по совету оракула отдать на съедение чудовищу свою любимую дочь Андромеду. Ее приковали к прибрежной скале. Каждую минуту Андромеда ожидала, что из морской пучины вынырнет Кит и проглотит ее. В это время герой древней Греции Персей совершал один из своих подвигов: он проник на уединенный остров на краю света, где обитали три страшные женщины – горгоны с клубками змей на голове вместо волос. Взгляд Горгоны превращал в камень все живое. Воспользовавшись сном горгон, Персей отсек голову одной из них по имени Медуза. Из ее тела выпорхнул крылатый конь Пегас. Две другие горгоны, проснувшись, хотели броситься на Персея, но он вскочил на крылатого Пегаса и, держа в руках драгоценную добычу – голову Медузы, полетел домой.
Пролетая над Эфиопией, Персей заметил прикованную к скале Андромеду. К ней уже направлялся Кит, вынырнувший из морской пучины. Персей вступил в смертельный бой с чудовищем. Одолеть кита удалось лишь после того, как на него упал леденящий взгляд мертвой головы Медузы. Кит окаменел, превратившись в небольшой остров. Персей расковал Андромеду, привел ее к Цефею, а впоследствии женился на ней.
Главных героев этого мифа фантазия древних греков поместила на небо. Так появились названия созвездий Цефея, Кассиопеи, Андромеды, Персея, Пегаса, Кита.
IV. Закрепление знаний и способов действий.
Построим вместе! Заданы координаты, построить звезду.
| 1) Созвездие «Андромеды» | |
| (–2;–1) (2;–2) (1;4) (–2;5) (–4;4) (–2;9) (0;7) (1;4) |
 |
| 2) Созвездие «Персея» | |
| (1;3) (1;1) (0;–1) (2;–2) (4;–1) (5;0) (6;2) (–5;–3) (–2;–2) (0;–1) |
 |
| 3)Созвездие «Пегаса» | |
| (–6;8) (–4;9) (0;8) (1;5) (8;5) (8;-2) (0;-1) (–2;–2) (–2;–4) |
 |
| 4) Созвездие «Кита» | |
| (2;0) (–3;0) (0;3) (2;0) (4;–1) (7;–1) (6;1) (2;0) (11;–7) (9;–6) (10;-5) (7;–1) (9;2) (6;1) |
 |
V. Самостоятельная работа.
Созвездие «Большой и Малой Медведицы»
Вариант 1
|
Вариант 2
|
Проверим ответ.
VI. Рефлексия
Важная тема,
Здорово,
Оценка урока – отлично,
Урок понравился,
Спасибо Декарту,
Мне было интересно
Есть вопросы
Ничего особенного
Было скучно
Узнал(а) много нового
Закончить наш урок, мне хотелось бы притчей.
Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?» И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго спросил: «А что ты целый день?» А тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»
Запомните эту притчу. На все окружающее нас, можно смотреть разными глазами, выражать разными словами, но из любой ситуации можно сделать вывод, двигающий нас вперед!
Домашнее задание:
Постройте звезду или созвездие, под которым вы родились и запишите историю этой звезды или созвездия.
Управление образования Топкинского муниципального района
Научно-практическая конференция исследовательских работ учащихся
«Первые шаги в науку»
математика
Координаты вокруг нас
Автор:
Чубукина Ольга Николаевна
Класс:6
Муниципальное образовательное учреждение
«Средняя общеобразовательная школа№1»
Научный руководитель:
Заборчук Наталья
Александровна, учитель
математики
ТОПКИ 2017
Оглавление
Введение………………………………………………………………………………3
1. Основная часть
1.1. История возникновения системы координат…………………………………….4
1.2. Координатная плоскость в математике…………………………………………….5
1.3. Координаты вокруг нас……………………………………………………………………7
1.4. Географические координаты……………………………………………………………8
2. Практическая часть
2.1.Построение изображений созвездий на координатной плоскости……….9
2.2.Создание «рисунков» в прямоугольной системе координат……………….10
Заключение ………………………………………………………………………………11
Литература …………………………………………………………………………………….12
Приложение ……………………………………………………………………………..13
Введение.
С координатами в жизни мы сталкиваемся постоянно, можно сказать «на каждом шагу». Идея задавать положение точки на плоскости с помощью чисел зародилась в древности — прежде всего у астрономов и географов при составлении звездных и географических карт, календаря.
Подробное изучение координатной плоскости необходимо. Ведь координаты- это тот же адрес. В повседневной жизни в речи взрослых мы иногда слышим такую фразу: “Оставьте мне свои координаты”. Это выражение означает, что собеседник должен оставить свой адрес или номер телефона, что и считается в этом случае координатами человека. Главное здесь в том, что по этим данным можно найти человека. Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта. Метод координат позволяет применять средства алгебры и математического анализа при решении геометрических задач. При работе с координатной плоскостью мы неоднократно можем менять расположение точек, размеры единичных отрезков, что требует высокого развития и логического мышления, и, следовательно, способствует его развитию. В окружающем нас мире существует много явлений и объектов-прообразов, которые можно использовать для составления заданий на метод координат. Если на уроках математики, каждой точке на числовой прямой ставилась в соответствии единственная координата (единственный адрес), то на уроках географии каждой точке на карте соответствуют уже два адреса, две координаты – долгота и широта. Например, координаты Кемерово: 37,60 восточной долготы и 55,80 северной широты. В математике встречается следующую запись: А (3; 5) – точке А сопоставлены в соответствие два числа, два адреса, две координаты. Так, значит, существует взаимосвязь между математическими координатами и географическими координатами. Весьма интересный материал предоставляет нам астрономия, где каждое созвездие тесно связанно с координатами.
Цель: выяснить , где еще кроме математики применяется система координат; исследование знаков зодиака через теорию координатной плоскости.
Задачи:
- Познакомиться с историей возникновения системы координат.
- Научиться свободно ориентироваться на координатной плоскости и на географической карте.
- Изучить зодиакальные созвездия.
- Построить изображение созвездия на координатной плоскости.
- Научиться «рисовать» в прямоугольной системе координат.
Гипотеза: Если термин «координатная плоскость» математический, то он используется только в математике
1.1. История возникновения системы координат.
История возникновения координат и системы координат начинается очень давно, первоначально идея метода координат возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи. Древнегреческого ученого Анаксимандра Милетского(610-546 до н. э.) считают составителем первой географической карты. Он четко описывал широту и долготу места, используя прямоугольные проекции. Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.
Первоначальное применение координат конечно связано с астрономией и географией, с потребностью определять положение светил на небе и определенных пунктов на поверхности Земли, при составлении календаря, звездных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта. Основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту (см.приложение 1,рис.1).
До наших времён дошла такая история, которая подтолкнула его к открытию. Занимая в театре места, согласно купленным билетам, мы даже не подозреваем, кто и когда предложил ставший обычным в нашей жизни метод нумерации кресел по рядам и местам. Оказывается эта идея осенила знаменитого философа, математика и естествоиспытателя Рене Декарта (1596-1650)– того самого, чьим именем названы прямоугольные координаты. Посещая парижские театры, он не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль, вызываемыми отсутствием элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.
Научное описание прямоугольной системы координат Рене Декарт впервые сделал в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Кроме того, в своей работе «Геометрия» (1637), открывшей взаимопроникновение алгебры и геометрии, Декарт ввел впервые понятия переменной величины и функции. «Геометрия» оказала огромное влияние на развитие математики. В декартовой системе координат получили реальное истолкование отрицательные числа.
Кроме математики интересы Декарта распространялись на физику, где он дал четкую формулировку закона инерции, открыл закон преломления световых лучей на границе двух различных сред («Диоптрика», 1637).
Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
1.2. Координатная плоскость в математике.
Каждый объект имеет свой упорядоченный адрес (координаты). Таким образом, адрес или координаты – это числовое или буквенное обозначение того места, где находится объект.
Математиками была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале). Такая модель получила название координатная плоскость.
Чтобы из обычной плоскости получить координатную, необходимо начертить две перпендикулярные прямые, отмечая стрелками направления «вправо» и «вверх» . На прямые наносят деления, как на линейку, причем точка пересечения прямых – это нулевая отметка для обеих шкал. Горизонтальную прямую обозначают и называют осью абсцисс, вертикальную прямую обозначают
и называют осью ординат.
Две перпендикулярные оси и
с разметкой называют прямоугольной, или декартовой, системой координат. Название «декартова» происходит от фамилии французского философа и математика Рене Декарта, который ее придумал (см.приложение 1,рис. 2).
Для любой точки на координатной плоскости можно указать два числа (координаты). На рисунке показана точка на координатной плоскости. Для получения координат этой точки необходимо через точку провести две прямые, параллельные координатным осям (обозначены пунктирной линией). Пересечение одной из прямых с осью абсцисс – это координата
точки
, пересечение другой прямой с осью ординат – это координата
точки
. Сначала указывают координату
, потом
. Точка
имеет координаты
. Аналогично находим координаты точки
, она имеет координаты
1.3. Координаты вокруг нас.
Системы координат пронизывают всю практическую жизнь человека. В нашей речи вы не раз могли слышать такую фразу: «Оставьте мне ваши координаты». Что означает это выражение? Догадались?! Собеседник просит записать свой адрес или номер телефона. У каждого человека бывают ситуации, когда необходимо определить местонахождение: по билету найдите место в зрительном зале или в вагоне поезда. Координаты окружают нас повсюду:
- чтобы правильно занять свое место в кинотеатре нужно знать две координаты — ряд и место (см.приложение1,рис.3)
- система географических координат (широта — параллели и долгота -меридианы) (см.приложение1,рис.4)
- те, кто в детстве играл в морской бой, тоже помнят, что каждая клетка на игровом поле определялась двумя координатами — буквой и цифрой (см.приложение1,рис.5)
- с помощью координатной сетки летчики, моряки определяют местоположение объектов;
- в биологии- построение схем молекул ДНК, построение диаграмм и графиков, прослеживающих эволюцию развития (см.приложение1,рис.6)
- в экономике- разнообразные системы координат применяются для построение графика спроса и предложения, при графическом изображении разных зависимых величин.
- в химии– построение таблицы Менделеева (изменение показателей происходит в горизонтальной и вертикальной плоскости)- взаимное расположение молекул .
- при астрономических наблюдениях координатная сетка накладывается на небесный свод с Землей в центре.
1.4. Географические координаты.
Так же, как и каждый дом имеет свой адрес (с названием улицы, города), также и каждое место на поверхности Земли можно записать в виде адреса, используя линию широты (параллель) и линию долготы (меридиан), проходящие через это место. Чтобы найти некоторый объект в городе, в большинстве случаев достаточно знать его адрес. Трудности возникают, если нужно объяснить, где находится, например, дачный участок, место в лесу. Универсальным средством указания местоположения служат географические координаты.
При попадании в аварийную ситуацию, человек первым делом должен уметь ориентироваться на местности. Иногда необходимо определить географические координаты своего местоположения, например, чтобы передать спасательной службе или для других целей.
В современной навигации стандартно используется всемирная система координат WGS-84. В этой системе координат работают все GPS навигаторы и основные картографические проекты в Интернете. Координаты в системе WGS-84 столь же общеупотребимы и понятны всем, как всемирное время.
Местоположение любого объекта на поверхности Земли, его «адрес», определяется географической широтой («адрес» по горизонтали) и географической долготой («адрес» по вертикали). Широта и долгота — это географические координаты точки земной поверхности
Географическая широта. Параллели — это линии широты. Для всех точек одной и той же параллели широта одинакова. Начало отсчета широт — экватор, все точки которого имеют нулевую широту. От экватора широта отсчитывается в градусах вдоль меридиана до заданной точки. Все точки земной поверхности, находящиеся к северу от экватора, имеют северную широту (с. ш.); широта точек к югу от экватора — южная (ю. ш.). Следовательно, широта показывает, насколько далеко к северу или к югу от экватора расположен заданный пункт. Как северная, так и южная широта отсчитываются от 0 до 90° (см.приложение 1,рис.7)
Географическая широта заданной точки определяется величиной в градусах дуги меридиана от экватора до параллели, проходящей у точку.
Географическая долгота. Долгота отсчитывается в градусах вдоль параллели. Началом отсчета долгот условно выбран Гринвичский (нулевой, начальный) меридиан, который проходит через старую Гринвичскую обсерваторию в Лондоне. Начальный меридиан и меридиан 180° разделяют Землю на Восточное и Западное полушария. Все точки Восточного полушария имеют восточную долготу (в. д.), а Западного — западную долготу (з. д.). Как восточная, так и западная долгота отсчитываются от 0 до 180°. Цифры, обозначающие градусы долготы, написаны на глобусе и на карте полушарий у точек пересечения меридианов с экватором. Географическая долгота заданной точки определяется величиной в градусах дуги параллели от начального меридиана до меридиана, проходящего через эту точку. (см.приложение 1,рис.8)
2.1. Построение изображений созвездий на координатной плоскости.
У древних греков существовала легенда о созвездиях Большой Медведицы и Малой Медведицы:«Всемогущий бог Зевс решил взять себе в жены прекрасную нимфу Калисто, одну из служанок богини Афродиты, вопреки желанию последней. Чтобы избавить Калисто от преследований богини, Зевс обратил Калисто в Большую Медведицу, а ее любимую собаку – в Малую Медведицу и взял их на небо» . Существует множество легенд и мифов о созвездиях. Фантазия древних греков поместила их на небо. Так появились созвездия Цефея, Андромеды, Персея и т.д. Знакомство с координатной плоскостью и вид звездного неба натолкнули на мысль, о переносе некоторых созвездий на координатную плоскость.
Созвездие Лев. В этом созвездии запечатлен Немейский Лев, над которым одержал победу Геракл.
Созвездие Близнецы. Созвездие названо в честь двух неразлучных братьев, сыновей Елены Прекрасной – Кастора и Полидевка..
Большая Медведица. Согласно греческому мифу это созвездие олицетворяет прекрасную нимфу Каллисто, превращенную Зевсом в Медведицу, чтобы спасти её от мести Геры.
Малая Медведица. Созвездие известно как Малый Ковш, последняя звезда в «ручке» которого – Полярная.
Орион. В греческой мифологии Орион – сын Посейдона и Эвриалы, великий охотник.
Телец. Созвездие названо в честь быка, на котором Европа переплыла море и попала к Зевсу на Крит. (см.приложение 2,рис.1)
2.2. Создание «рисунков» в прямоугольной системе координат.
На координатной плоскости интересно строить рисунки, используя построение графов по координатам. Нужно сначала нарисовать рисунок, а затем его перенести на координатную плоскость, но при этом плавные соединения должны быть в виде отрезков.
(см.приложение 2,рис.2)
Заключение.
Таким образом, в результате проведения исследования, мной были решены поставленные задачи. А именно, я изучила координатную плоскость и связанные с ней понятия. Кроме того, мне удалось определить возможность создания графического изображения на координатной плоскости, то есть создать рисунок по известным координатам, а также перенести изображения созвездий с астрономической карты на координатную плоскость.
В результате проведения исследования выдвинутая гипотеза не получила подтверждение. Я доказала, координатная плоскость используется не только в математике, а пронизывает всю практическую жизнь человека; исследовала знаки зодиака через теорию координатной плоскости.
В настоящее время координатный метод широко применяется в повседневной жизни. Современные системы спутниковой навигации позволяют определять координаты объекта, а также следить и управлять объектами, в том числе и движущимися. Эта тема также представляет сегодня большой интерес и может стать темой новой исследовательской разработки в будущем.
Литература
- Бахтина Е.Н. Книга звёзд. Москва «Интербук», 1997.
- Зубарёва И.И., А.Г.Мордкович А.Г. Учебник математики 6 класс.
- Савин А.А. Координаты // Квант. 1977. №9
- Интернет-источник zodiac-art.narod.ru
- Интернет – источник https://ru.wikipedia.org/.
Приложение 1
Рис.1 Рене Декарт
Рис.2 Координатная плоскость
Рис.3
Рис.4
Рис.5
Рис.6
Рис.7
Рис.8
Приложение 2
Рис.1
Рис.2
«Жираф»
(1;11) (9;-12) (-6;1)
(3;12) (10;-13) (-8;-5)
(8;13) (10;-14) (-9;-10)
(13;11) (9;-14) (-9;-12)
(16;-8) (9;-15) (-10;-13)
(17;6) (8;-15) (-9;-14)
(17;4) (7;-14) (-10;-15)
(15;2) (7;-13) (-11;-14)
(18;0) (6;-13) (-12;-15)
(15;0) (3;-7) (-13;-14)
(16;-3) (3;-5) (-12;-12)
(15;-5) (1;-1) (-11;-12)
(15;-7) (-2;-1) (-11;-10)
(14;-9) (-3;-4) (-10;-7)
(12;-11) (0;-13) (-10;-4)
(12;-12) (0;-14) (-9;0)
(10;-12) (-1;-13) (-10;6)
(8;-10) (-2;-14) (-8;9)
(7;-8) (-3;-14) (-6;11)
(9;-5) (-4;-13) (-7;12)
(10;-2) (-3;-12) (-12;10)
(10;-1) (-3;-10) (-8;14)
(7;-1) (-4;-7) (-5;13)
(12;2) (-6;-15) (-3;13)
(14;5) (-5;-16) (1;11)
(12;8) (-6;-17)
(9;9) (-7;-16) Глаза:
(4;6) (-7;-17) (11;-2)
(4;3) (-8;-16) (13;-2)
(3;0) (-8;-15)
(4;-1) (-7;-14) Нос:
(5;-5) (-8;-13) (10;-10)
(8;-12) (-5;-3) (11;-10)
«Слонёнок»
(2;4) (10;-5) (7;1) (11,5;-1)
(2;1) (10;-9) (5;1) (10,5;-3,5)
(3;0) (12;-9) (4;0) (9;-4)
(4;1) (12;-3) (3;1) (7;-3)
(3;-1) (13;-7) (3;4) (7;-1)
(5;-3) (13;-3) (2;4) Глаза:
(6;-3) (12;1,5) Ухо: (5;0)
(6;-9) (10;-1) (7;1) (6;0,5)
(8;-9) (8;-1) (9;1,5) (7;0)
(8;-5) (8;0) (11;0,5) (6;-0,5)
«Кит»
(0;9) (-2;-8) (7;-10) (12;-9)
(-1;-11) (0;-7) (-1;-10) (10;-10)
(-3;13) (1;-6) (-3;-8) (9;-9)
(-4;12) (3;-5) (-1;-9,5) (10;-7)
(-2;8) (5;-6) (0;-8) (9;-3)
(-2;5) (7;-7) (1;-10) (4;2)
(-4;3) (9;-9) (2;-7) (4;2)
(-5;1) (3;-6) (3;-10) (1;7)
(-5;-5) (1;-7) (4;-7) (4;12)
(-4;-7) (-1;-7) (5;-10) (3;13)
(-3;-8) (-3;-8) (6;-8) (1;11)
(-5;-8) (-2;-10) (7;-10) (0;9)
(-6;-10) (0;-11) (7;-9) Точка:
(-4;-9) (6;-11) (9;-9) (-2;-7)
(-3;-8) (9;-9) (10;-8) (8;-7)
«Лось»
(-5,5;2) (-4;3) (-3;3,5) (-0,5;3,5)
(1;4,5) (2,5;4,5) (3,5;5,5) (4,5;5,5)
(3,5;6) (2,5;7,5) (2,5;8) (3,5;8,5)
(4;7,5) (4,5;8,5) (5;7) (5;8)
(5,5;7,5) (6;7,5) (6;6,5) (7,5;7)
(7;6) (5,5;5,5) (8;5) (8,5;4)
(8,5;3,5) (8;3) (7;3,5) (6;2,5)
(5;2,5) (4,5;1) (4,5;0) (3,5;-1)
(3;-3) (3;-4) (2,5;-5) (2,5;-7)
(3,5;-8,5) (2,5;-8,5) (2;-7,5) (2;-1,5)
(1,5;-1,5) (0,5;-5) (0,5;-8)
(1;-8,5) (0;-8,5) (-0,5;-7,5) (0;-7)
(0;-2) (-1;-1) (-2,5;—0,5) (-3,5;-2)
(-3,5;-2,5) (-4,5;-3,5) (-4,5;-7) (-3,5;-8,5)
(-4,5;-8,5) (-5,5;-5) (-5,5;-3,5)
(-5;—2,5) (-5;—1) (-6;1)
(-5,5;2) и
(-5;-2) (-6,5;-3,5) (-6,5;-5) (-7;-7)
(-6,5;-8) (-5,5;-8) (-6;-7) (-6;-5)
(-5,5;-3,5) и
(6;5)
«Крокодил»
(15;2) (-5;-3) (7;-4)
(15;3) (-6;-4) (6;-3)
(10;1) (-3;-4) (8;-4)
(9;2) (-2;-3) (10;-4)
(8;2) (-1;-4) (8;-3)
(7;1) (1;-4) (15;0)
(3;1) (0;-3) (10;0)
(-4;0) (4;-3) Глаз:
(-16;-2) (4;-4) (9;1)
Карточка № 1
Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(3;3); (0;3); (-3;2); (-5;2); (-7;4); (-8;3); (-7;1); (-8;-1);
(-7;-2); (-5;0); (-1;-2); (0;-4); (2;-4); (3;-2); (5;-2); (7;0); (5;2);
(3;3); (2;4); (-3;4); (-4;2); глаз (5;0).
Карточка № 2
Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(3;0); (1;2); (-1;2); (3;5); (1;7); (-3;6); (-5;7); (-3;4);
(-6;3); (-3;3); (-5;2); (-5;-2); (-2;-3); (-4;-4); (1;-4); (3;-3);
(6;1); (3;0); глаз (-1;5).
Карточка № 3
Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(1;7); (0;10); (-1;11); (-2;10); (0;7); (-2;5); (-7;3); (-8;0);
(-9;1); (-9;0); (-7;-2); (-2;-2); (-3;-1); (-4;-1); (-1;3); (0;-2);
(1;-2); (0;0); (0;3); (1;4); (2;4); (3;5); (2;6); (1;9); (0;10); глаз (1;6).
Карточка № 4
Рисуем по координатам
Нарисовать животное на плоскости по его заданным координатам.
(Отметить точки на координатной плоскости, соседние точки соединяются отрезками).
(1;-4); (1;-6); (-4;-6); (-3;-5); (-1;-5); (-3;-4); (-3;-3);
(-1;-1); (-1;0); (-3;0); (-3;-1); (-4;-1); (-4;0); (-3;1); (-1;1);
(-1;2); (-3;3); (-1;4); (0;6); (1;4); (1;2); (3;4); (6;5); (9;2); (9;0);
(9;-4); (6;-4); (5;-1); (4;-1); (1;-4); глаз (-1;3).
Ответы: 2 – утенок; 3 – заяц; 4 – белка; 5 – кошка.
С помощью этой системы осуществляется решение задач в геометрии, а также в других научных дисциплинах.
Кроме того, принцип указания точного адреса объекта с помощью двух величин получил широкое распространение во многих отраслях человеческой деятельности.
Системы координат
Под понятием координат в повседневной жизни понимается упорядоченный набор слов, цифр и прочих знаков, позволяющий определить местоположение человека, здания или другого объекта. Эти знания необходимы для ориентирования в современном обществе и организации любой человеческой деятельности.
Трудно даже представить себе мир без системы адресов и нумерации.
Примеры использования:
- почтовый адрес;
- номер места в театре, автобусе или самолёте;
- обозначение положения фигур на шахматной доске;
- географическая широта и долгота.
Таким образом, система координат необходима не только в математике.
Она буквально пронзает всю человеческую жизнь.
Без применения этих научных знаний люди не смогли бы значительно отдалиться от животных и первобытных предков.
Некоторые области применения:
- Геометрия довольно часто пользуется методикой нахождения точки на координатной плоскости или в пространстве.
- Математика — построение графиков функций.
- География использует собственные координаты (широта и долгота).
- Астрономия определяет положение небесных объектов во вселенной.
По определению любая координатная система представляет собой ряд идентификационных данных, которые позволяют узнать положение точки или фигуры в пространстве, а также дают возможность проследить её перемещение.
Наибольшее распространение получила прямоугольная система координат, которую ещё называют декартовой, по имени создателя Рене Декарта. Её популярность основана на простоте и универсальности.
Другие виды координат:
- полярные;
- цилиндрические;
- сферические;
- косоугольные;
- биангулярные;
- биполярные;
- конические;
- бицентрические;
- координаты Риндлера;
- бицилиндрические;
- параболические;
- тороидальные;
- проективные;
- трилинейные;
- эллипсоидальные.
Видя такое множество, можно смело сказать, что задать координаты на плоскости, в двумерном или трёхмерном пространстве можно бесчисленным количеством способов. Для решения определённой задачи стоит выбирать наиболее подходящий метод из всех имеющихся.
Координатная плоскость
Прямоугольная или квадратная система координат была изобретена ещё в XVII веке. Благодаря своей невероятной гениальности, простоте и понятности для большинства людей, она получила широчайшее распространение и с успехом применяется до сих пор.
Чтобы построить фигуру на координатной плоскости, нужно изобразить две линии пересекающиеся под прямым углом:
- Ось X’X.
- Ось Y’Y.
Точка пересечения O является началом отсчёта, из неё откладываются все значения в координатной системе. Стоит помнить, что вправо и вверх идут положительные величины, а влево и вниз — отрицательные. Таким образом, две оси образуют квадранты координатной плоскости (четверти). В зависимости от того, в каком из четырёх образовавшихся сегментов находится точка или фигура, будет изменяться её значение.
Местоположение любой точки на координатной плоскости определяется при помощи двух числовых показателей. Первый — это абсцисса x, он откладывается по горизонтали и равен отрезку ОВ. Второй — ордината y, откладывающаяся по вертикали и совпадающая с отрезком ОС.
Выходит, что для задания и записи точного местоположения любой точки А необходимо измерить её расстояние до оси абсцисс и ординат. Схематическая запись координат будет выглядеть как А (x, y) или xА, xB, возможны и другие варианты.
Обычно на практике применяют правостороннюю координатную систему. В этом случае адрес точки принимает положительное значение лишь в правом верхнем квадранте I, образованном правой частью оси ординат (X) и верхней частью оси абсцисс (Y). Иногда бывают ситуации, в которых использование другой ориентации является более целесообразным.
Не стоит считать, что декартовая координатная система может применяться только на плоскости. Она вполне подходит для любого пространства, имеющего конечную размеренность. Всё становиться более сложным — для каждого дополнительного измерения создаётся новая ось.
Для нахождения местоположения точек в привычном трёхмерном пространстве, помимо абсциссы и ординаты, вводится третья координата, именуемая аппликатором (z). Для этого через точку O проводится дополнительная ось, изображающая третье измерение и являющаяся перпендикулярной к двум остальным. В этом случае создаётся своеобразная объёмная решётка, а пространство разделяется линиями на 8 частей — октантов.
При рисовании такой системы на листе применяется проекция на плоскость. Третья ось проводится под углом в 45 градусов к остальным, создавая иллюзию трёхмерного пространства.
Историческая справка
Сегодня каждый школьник, учащийся в шестом классе, не только слышал про координатную плоскость, но и знает правило построения простейших фигур в двумерном пространстве. Но так было не всегда.
Необходимость в определении точного местоположения объектов возникла очень давно. Скорее всего, ещё в древнейшие времена существовали примитивные методы записи координат. Более точные системы возникли в Древней Греции. Их появление было связано с потребностью в картографии.
Достоверно известно, что составитель первой карты Анаксимандр Милетский пользовался географической долготой и широтой, запись которых была основана на прямоугольной проекции. Незадолго до начала нашей эры древнегреческий учёный по имени Гиппарх выдвинул замечательную идею, заключающуюся в опоясывании земного шара параллелями и меридианами и записи информации о положении объектов в виде двух чисел. В Египте на стене одной из усыпальниц археологами был обнаружен рисунок, состоящий из клеточек и представляющий собой координатную сетку.
Автором прямоугольной системы координат на плоскости является математик Рене Декарт, живший во Франции XVII века. История этого гениального открытия весьма забавна. Дело в том, что в театре тех лет ещё не существовало привычной для современной публики нумерации мест. Из-за этого нередко возникала страшная путаница, ссоры, драки и даже дуэли. Будучи талантливым математиком, Декарт предложил новый способ обозначения, базирующийся на двух номерах — ряда и кресла. Это изобретение избавило зрителей от ненужных проблем и произвело настоящий фурор в обществе.
Позже учёный изложил принципы плоскости координат, а также прочие открытия в своём фундаментальном труде «Геометрия». Первые попытки применить метод Декарта к трёхмерному пространству были предприняты в XVIII веке Леонардом Эйлером.
Сегодня при помощи декартовой системы координат можно задать не только расположение простой фигуры, например, треугольника, на плоскости, но и описать любой сложный предмет и его перемещение в пространстве. Метод нашёл широкое применение во многих электронных устройствах и графических программах.
Особенности использования в географии
С развитием современных технологий определение географических координат очень упростилось.
Достаточно запустить одно из навигационных приложений или войти в специальный онлайн-сервис, и местоположение будет указано с максимальной точностью.
Поверхность земли имеет сферическую форму, из-за этого географическая система координат имеет свои особенности.
Обозначение любой точки на планете осуществляется при помощи набора цифробуквенных обозначений:
- широта бывает северная и южная;
- долгота — восточная и западная;
- высота над уровнем моря.
Все точки одной широты соединяются параллелями. На экваторе широта составляет 0 градусов, а на полюсе 90. Меридианы соединяют точки с одним и тем же показателем долготы и сходятся на полюсах.