Рассказ про механическое движение

• Энциклопедия
• Разное
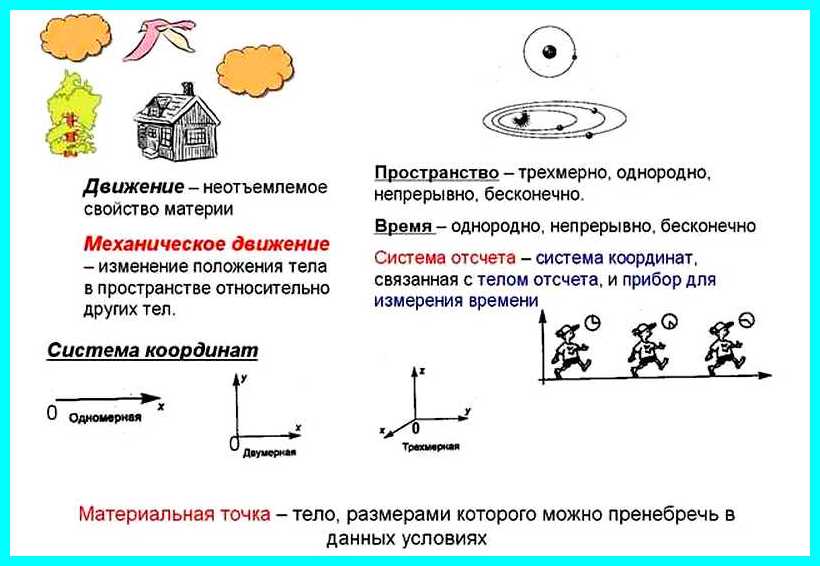
• Механическое движение

Рассмотрим теоретические понятия механического движения. Это изменяющее положение тела его частей относительно других частей с течением периода. Механика возникла для решаемых потребностей человека для изучения сил природы, чтобы их использовать.

Раздел механики, раскрывающей определенные методы, изучающие механическое движение тел без выявления обстоятельств двигательного характерного свойства.  Являющие обстоятельства не рассматриваются в данном разделе, их можно наблюдать в других разделах. Как понять, что тело находится в постоянном движении?

Линия, по которой направляется оно, называют траекторией.  Точки, способствующие перемещаться за определенное время, называют направлениями, а конец – окончательным положением.

Тело точки, когда оно перемещается, можно определить окончательной и начальной координатами тела и не рассматривать зависимость от факта, в какую сторону направляется тело в течение периода. Оно проходит расстояние за определённое время, которое называют путем. Длину обозначают путем. Если тело не меняло свои свойства в двигательном направлении, находилось в одном положении, то путь, пройденным телом, равен модулю его перемещения. Если тело изменялось, путь выше перемещаемого и модуля, и другого модуля.

Рассмотрим теоретическое понятие пути.

Путем называется величина, при которой равно нулю при факте, если за период тело было закреплено в одном положении. Путем называют величину, равняющей длине траектории за определенный период. Чтобы измерить движения пути можно использовать разнообразные инструменты для измерения линейных величин: линейки и другие.

Далее рассмотрим следующие ниже перечисленные понятия.

Движение прямолинейно в том случае, если тело направляется по прямому отрезку. Криволинейным называют кривую линию, которая движется таким образом.

Чтобы указать определенные свойства тела, первым делом выражается в следующем:

1. в выборе отсчета и его начала на теле;
2. в связывающих свойствах оси координат через начало отсчета в определенное направление.

Координатой тела называют пройденное расстояние от начала отсчета до данного тела. Координата выражается в единицах длины.

Системой отсчета называют тело отсчета, связанного с координатами. Если она не изменялась в течение периода, то можно заявить об утверждении того аспекта, что тело в системе отсчета неподвижно или находится в состоянии покоя.

Если координатная ось тела проходит увеличенный отсчет, то можно утверждать, что тело направляется к своей цели положительно. И, наоборот, если снижается, то можно утверждать, что оно направлено отрицательно.

Нет такой возможности утверждения движения тела, если не рассматривать систему отсчета. Другими словами, можно утверждать, что тело в разнообразных точках отсчета имеют различные направления движения (или может не двигаться).

Механика – сложный раздел науки, изучающая природные свойства. Механику изучают с целью их использования в своих человеческих потребностях.

Доклад №2

Движение любого предмета или тела по отношению к другим предметам в пространстве и во времени называется механическим движением. Термин произошёл от латинского слова «mechanicus». В природе механические движения совершают реки, облака, животные и люди. Созданные людьми поезда, автомобили, водный и авиационный транспорт тоже осуществляют механические движения. В физике исследованием механического движения занимается механика. Из истории известно, что древние греки, египтяне и римляне строили механизмы, в которых происходили механические движения составных частей. С тех времён началось изучение механики как науки.

Любое движение или покой считается относительным. Например, сидящий в машине человек, находится в состоянии покоя по отношению к своему автомобилю. Но по отношению к предметам вне машины, он движется.

Невозможно однозначно ответить, движется предмет или нет. Это можно сделать, только зная, относительно какого предмета происходит движение.

Движение без уточнения причин его возникновения, называется кинематикой.

Для рассмотрения движения тела, требуется определить, как меняется расположение всех точек тела в течение времени. Каждая точка очерчивает линию, которую называют траекторией. Линия, написанная в тетради ручкой, будет являться траекторией движения этой ручки. Пути прохождения точек могут быть разнообразными. Траектория может иметь вид прямой линии, будет называться прямолинейным движением, и кривой линии (криволинейное движение).

Когда все точки наблюдаемого предмета движутся идентично, то такое движение будет называться поступательным. Если точки тела вращаются около окружности, тогда движение называется вращательным. Вращательные движения широко распространены в технике (оси, шестерни и пр.). Обращение планет вокруг своей оси тоже является вращательным движением. Третья разновидность механического движения – колебательное движение. Это такое движение, которое периодически повторяется в двух противоположных направлениях. Например, игла в швейной машинке.

Итак, для полного описания механического движения тела необходимо определить положение тела, знать траекторию, обозначить место нахождения тела в нужный отрезок времени и длину пути тела. Для этого нужно уметь измерять длину пути движения и отрезок времени для прохождения этого пути.

Единицами измерения длины служат метры, сантиметры т. п. Измерителями времени являются секунды, минуты, часы и т. д.

7 класс по физике

Механическое движение

Популярные темы сообщений

• Творчество Казакова

  Юрий Павлович Казаков (1927-1982гг) – советский писатель, сценарист и драматург. Вырос Казаков в обыкновенной семье в Москве. Он выучился в строительном техникуме,

• Астрид Линдгрен

  «Волшебница из Швеции» – так во всем мире уважительно называют великую сказочницу Астрид Анну Эмилию Линдгрен (1907 – 2002), из-под пера которой вышли десятки чудесных историй,

• История Санкт Петербурга

  История Санкт-Петербурга является необычной по сравнению с возведением других городов. Ведь город не возник в результате эволюционного развития уже существующего населения. Санкт-Петербург возвели с нуля камушек за камушком,

• Некрасов

  Н.А.Некрасов внес в русскую литературу огромный вклад. Вся его жизнь это большая увлекательная история, которая не оставила равнодушным не одного человека. Поэт появился на свет в 1821 г. 28 ноября на Украине. Его семья была крепостного дворянина.
• Природные зоны России

  Территория России протянулась на 17,1 миллиона квадратных километров с севера на юг. Как не в одной из стран мира наша страна-это многообразие растительного и животного мира.

«Механическое движение. Траектория и путь»

Механическое движение — это изменение положения тела или его частей относительно других тел с течением времени. Механическое движение — это изменение положения тела или его частей относительно других тел с течением времени. Изучение механики традиционно начинают с кинематики.

Кинематика — раздел механики, в котором рассматривают способы описания механического движения тел без выяснения причин изменения характера их движения. Сами причины рассматриваются в других разделах механики.

Траектория движения — это линия, вдоль которой движется тело.

Перемещением точки за промежуток времени называют направленный отрезок прямой, начало которого совпадает с начальным положением точки, а конец — с конечным положением точки. Перемещение точечного тела определяется только конечной и начальной координатами тела и не зависит от того, как двигалось тело в течение рассматриваемого промежутка времени.

Путь — это длина траектории, пройденной телом. Путь — всё расстояние, пройденное точечным телом за рассматриваемый промежуток времени.

Если тело в процессе движения не меняло направления движения, то пройденный этим телом путь равен модулю его перемещения. Если тело в течение рассматриваемого промежутка времени меняло направление своего движения, путь больше и модуля перемещения тела, и модуля изменения координаты тела.

Путь всегда величина неотрицательная. Он равен нулю только в том случае, если в течение всего рассматриваемого промежутка времени тело покоилось (стояло на месте).

Виды траекторий. Если тело движется вдоль прямой, движение называют прямолинейным. Траектория в этом случае — отрезок прямой. Если же траектория — кривая линия, движение называют криволинейным.

Относительность движения

Для того чтобы описать положение данного тела в пространстве, необходимо:

1. выбрать тело отсчёта и начало отсчёта на нём;
2. связать с ним координатную ось, проходящую через начало отсчёта в нужном направлении, и указать единицу длины.

При этом расстояние от начала отсчёта до данного тела, выраженное в выбранных единицах длины и взятое с соответствующим знаком, называют координатой этого тела.

Система отсчета

Поступив так, мы будем говорить, что описали положение данного тела относительно выбранного тела отсчёта. Если мы выберем в качестве тела отсчёта другое тело или другую ось координат, то и координата данного тела может стать другой. Совокупность тела отсчёта, с которым связана ось координат, и часов называют системой отсчёта.

Если координата тела не изменяется с течением времени в выбранной системе отсчёта, то говорят, что это тело в данной системе отсчёта неподвижно, или покоится.

Если координата тела выбранной системы отсчёта увеличивается со временем, то говорят, что тело движется в положительном направлении координатной оси. Напротив, если координата тела в выбранной системе отсчёта со временем уменьшается, то говорят, что тело движется в отрицательном направлении координатной оси.

Нельзя сказать, как движется тело, если не сказать, в какой системе отсчёта рассматривается это тело. Иначе говоря, одно и то же тело в разных системах отсчёта может двигаться по-разному (в том числе и покоиться).

---

Конспект по физике в 7 классе по теме «Механическое движение. Траектория».

Следующая тема: Прямолинейное равномерное движение

Определения

Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.

Основная задача механики — определение положение тела в пространстве в любой момент времени.

Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение и его виды

По характеру движения точек тела выделяют три вида механического движения:

• Поступательное. Это движение, при котором все точки тела движутся одинаково. Если через тело мысленно провести прямую, то после изменения положения этого тела в пространстве данная прямая останется параллельной самой себе.
• Вращательное. Это движение, при котором все точки тела движутся, описывая окружности.
• Колебательное. Это движение тела, которое повторяется точно или приблизительно через определенные интервалы времени. От вращательного движения его отличает то, что при колебаниях тело перемещается в двух взаимно противоположных направлениях.

По типу линии, вдоль которой движется тело, выделяют два вида движения:

• Прямолинейное — тело движется по прямой линии.
• Криволинейное — тело движется по кривой линии, в том числе замкнутой.

По скорости выделяют два вида движения:

• Равномерное — скорость движущегося тела остается неизменной.
• Неравномерное — скорость движущегося тела с течением времени меняется.

По ускорению выделяют три вида движения:

• Равноускоренное — тело движется неравномерно с постоянным ускорением (положительным). Скорость увеличивается.
• Равнозамедленное — тело движется неравномерно с постоянным замедлением (отрицательным ускорением). Скорость уменьшается.
• Ускоренное — тело движется неравномерно с меняющимся ускорением. Скорость может, как увеличиваться, так и уменьшаться.

Что нужно для описания механического движения?

Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.

Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.

Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.

Тело отсчета — тело, относительно которого рассматривается движение.

Часы — прибор для отсчета времени. Время измеряется в секундах (с).

При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.

Виды систем координат

В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:

• Одномерную. Используется, когда положение материальной точки можно задать только одной координатой x — M(x) . В этом случае тело движется прямолинейно.
• Двумерную. Используется, когда положение материальной точки можно задать двумя координатами x и y — M(x,y). Тело в этом случае движения по плоскости.
• Трехмерную. Используется, когда положение материальной точки можно задать тремя координатами x, y и z — M(x,y,z). Тело в этом случае изменяет положение в трехмерном пространстве.

Способы описания механического движения

Описать механическое движение можно двумя способами:

1. координатным
2. векторным

Координатный способ

Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:

Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.

Векторный способ

Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.

Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:

Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.

Характеристики механического движения

Движение материальной точки характеризуют три физические величины:

1. перемещение
2. скорость
3. ускорение

Перемещение

Определение

Перемещение (вектор перемещения) — направленный отрезок, начало которого совпадает с начальным положением точки, а конец — с его конечным положением. Обозначается как S.

Перемещение точки определяется как изменение радиус-вектора. Это изменение обозначается как Δr. С точки зрения геометрии вектор перемещения равен разности радиус-векторов, задающих конечное и начальное положение точки:

Траектория — линия, которую описывает тело во время движения.

Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).

Путь есть функция времени:

Модуль перемещения — длина вектора перемещения. Обозначается как |Δr|. Единица измерения — метры (м).

Внимание!

Модуль перемещения необязательно должен совпадать с длиной пути.

Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.

Путь равен длине окружности. Поэтому:

Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.

Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?

Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:

Скорость

Определение

Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.

В физике скорость обозначается V. Математически скорость определяется формулой:

Скорость характеризуется не только направлением вектора скорости, но и его модулем.

Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).

Математическое определение модуля скорости:

Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:

Ускорение

Определение

Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.

В физике ускорение обозначается a. Математически оно определяется формулой:

Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с²).

Математическое определение модуля скорости:

v — скорость тела в данный момент времени, v₀— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.

Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:

Проекция вектора перемещения на ось координат

Определение

Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.

Проекция вектора на ось OX:

Проекция вектора на ось OY:

Знаки проекций перемещения

• Проекция является положительной, если движение от начала проекции вектора к проекции конца происходит сонаправленно оси координат.
• Проекция является отрицательной, если движение от начала проекции вектора к проекции конца направлено в сторону, противоположную направлению координатной оси.

Внимание!

Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.

Модуль перемещения — длина вектора перемещения:

Модуль перемещения измеряется в метрах (м).

Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:

Выразив проекции вектора перемещения через координаты, эта формула примет вид:

Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:

Общий вид уравнений координат:

Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.

Определяем координаты начальной точки вектора:

Определяем координаты конечной точки вектора:

Проекция вектора перемещения на ось OX:

Проекция вектора перемещения на ось OY:

Применяем формулу для вычисления модуля вектора перемещения:

Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.

Извлекаем известные данные:

Для определения координаты точки В понадобятся формулы:

Выразим из них координаты конечного положения точки:

 

Точка В имеет координаты (5; 10).

Алиса Никитина | Просмотров: 35.9k

План урока:

Главная особенность механического движения

Скорость движения. Первые задачи по физике

Вектор – число и направление

Основная задача механики

Главная особенность механического движения

Раздел физики, который называется механикой, изучает движение, описывает и характеризует его, выясняет причины движения и покоя.

                                                

Изменение положения одних тел относительно других механическим движением называется. Дети перемещались относительно жилых домов, школы, деревьев. А вот одежда школьников как была на них, так и осталась. А если дети добирались до стадиона на автобусе? Они перемещались относительно домов, столбов, пешеходов, но не двигались по отношению к  водителю, креслам, самому автобусу.

Главная особенность механического движения состоит в том, что оно относительно. Какое расстояние проходит ученик седьмого класса, пока длится урок в школе? «Никакое», — скажут те, кто отсчитывает расстояние от школьной парты. «81 000 км», — ответят другие, кто учитывает, что ученик вместе со школой и Землей движется вокруг Солнца со скоростью 108 000 км/ч. Значит, относительно парты школьник в течение урока не движется, а относительно Солнца преодолевает большое расстояние.

Тело движется, оставляет след, или этот след можно мысленно представить. В физике линия, вдоль которой тело движется, называется траекторией. Когда баскетболист отдает пас напарнику, мяч летит по прямой – траектория прямолинейная. Когда вратарь бросает в поле мяч, то он летит по кривой линии – криволинейная траектория.

     

Самую сложную траекторию для изучения разбивают на прямолинейные и криволинейные участки.

Движение характеризуется пройденным путем или длиной траектории. Лыжня – это траектория, а длина лыжни – дистанция или пройденный лыжником путь. Траектория кончика часовой стрелки – это окружность, пройденный путь – длина окружности.

Пройденный путь обозначают буквой s. Это расстояние или длина, поэтому измеряется в метрах.

(Источник)

Движение, кроме траектории, описывается путем за единицу времени, т.е. за одну секунду. Если этот путь остается неизменным, то движение равномерное (за одну секунду одинаково), в противном случае – неравномерным (неодинаково за одну секунду).

Из большого количества различных видов движений самое простое – прямолинейное движение. В действительности такие движения крайне редки. Автомобиль, спортсмен, мотоцикл, самолет и другие движущиеся тела лишь небольшие промежутки времени участвуют в прямолинейном равномерном движении.

Итак, для запоминания:

Скорость движения. Первые задачи по физике

Урок физкультуры. Идут школьные соревнования по бегу. Как ни старался Артем (он пробежал 60 м за 12 секунд), место победителя досталось Денису, пробежавшему дистанцию за 10 секунд. Значит, Денис бежал быстрее соперника. На прохождение того же пути ему понадобилось меньше времени.

Что же характеризует быстроту движения? Семиклассникам знакомо слово «скорость», которое как раз и определяет быстроту движения. Скорость самолета больше скорости автомобиля, но меньше скорости ракеты.

Самая большая скорость в природе у света (300 000 км/с), ничто не может двигаться быстрее, чем свет.

Как найти скорость? В приведенном примере Денис 60 м пробежал за 10 с., значит, за секунду он пробегал по 6 м, а Артем на 60 м затратил 12 с времени, т. е. за 1 с он пробегал по 5 м. Денис опережал Артема на 1 м в течение одной секунды, а значит, бежал быстрее.

Скорость – это путь, проходимый телом за единицу времени. При решении задач нерационально каждый раз записывать правило, показывающее, как найти нужную величину, например, «Для вычисления скорости, надо пройденный путь разделить на время этого пути», затем составлять числовое выражение и считать. Поэтому в физике и других науках используется понятие «формула». Формула – это правило, записанное с помощью букв.

 Если ввести условные буквенные обозначения: скорость – v, пройденный путь – s, время – t, то правило вычисления скорости запишется коротко и ясно:

v = s / t

Это самая первая формула физики седьмого класса. Она называется формула скорости. Формулы важно запоминать и уметь применять для конкретных задач.

Измеряется скорость в м/с (СИ), т. е. единица пути делится на единицу времени, следуя формуле. Используются разные единицы. Например, движение транспорта чаще измеряется в км/ч.

 Например, нарушает ли водитель правила, если легковой автомобиль движется со скоростью 20 м/с, а на обочине стоит знак с ограничением скорости «60»? На дорожных знаках скорость берется в км/ч. Значит, скорость автомобиля тоже надо перевести в км/ч. 1 м = 0,001 км, 1 ч = 3600с.

20 м/с = 20 ∙ 0, 001 ∙ 3600 км/ч = 72 км/ч.

Следует вывод: водитель нарушил правила дорожного движения.

А теперь нужно научиться правильно решать и оформлять физические задачи. Существует определенный порядок решения:

1. Условие задачи записать в сокращенном виде;
2. Выразить заданные величины в СИ;
3. Записать нужную формулу;
4. Проделать математические вычисления;
5. Получившийся результат записать в ответе.

Задача первая: Попрыгунья стрекоза летает со скоростью 36 км/ч, а скворец – 12 м/с. Догонит ли скворец стрекозу?

     Образец оформления задачи:

Задача вторая: Гепард считается самым быстрым животным в мире. В погоне за добычей 36 км он пробегает за 20 минут. Чему равна скорость гепарда?

     Образец оформления задачи:

Зная скорость, легко определить и пройденный путь. Например, акула имеет скорость 10 м/с, значит, за 1 с она проплывет 10 м, за 2 с – 20 м, за 3 с – 30 м и т.д. А за 15 с? Надо скорость умножить на время. Получится 150 м. Для пройденного пути также есть правило, записать которое можно в виде формулы пути:

s = v ∙ t

а формула времени имеет вид:

t = s / v

Задача третья: Старик Хоттабыч с Волькой и Мишкой на машине «Волга», двигающейся со скоростью 108 км/ч, отправились за город. До привала они ехали 2 часа. На каком расстоянии от города был сделан привал?

     Решение:

В случае этой задачи единицы в СИ переводить не надо. Они соответствуют друг другу (время дано в часах и скорость в километрах в час, а не в метрах в секунду) и дают реальное представление о времени и расстоянии.

В приведенных примерах считалось, скорость не менялась на всем пути, т. е. движение было прямолинейным и равномерным. А как быть с неравномерным движением? Из его определения получается, что скорость тела различна на отдельных участках пути.

Неравномерное движение характеризуется другой величиной – средней скоростью. Чтобы ее найти надо путь (пусть он даже состоит из отдельных участков) разделить на полное время движения.

v_ср = s / t

Средняя скорость волка при беге 16 м/с, это вовсе не значит, что он все время бежит с этой скоростью. Один участок пути он бежит со скоростью 18 м/с, другой – со скоростью 14 м/с, а в среднем – 16 м/с.

Иногда среднюю скорость считают скоростью равномерного движения. Например, автобус движется со скоростью 60 км/ч. Но ведь это его средняя скорость. У остановок автобус тормозит, а потом набирает скорость, на гладких участках дороги едет чуть быстрее, на неровностях медленнее. Вот и берется скорость, которая получается в среднем.

Скорость – значит быстро или медленно.

Вектор – число и направление

Если где-то используется знак стрелки, то ясно, что она показывает направление, в котором следует двигаться. А скорость имеет направление? Где будет находиться автобус, если он движется от остановки со скоростью 70 км/ч? Местоположение автобуса не назвать, так как неизвестно, куда автобус едет от остановки, в каком направлении. Скорость имеет и численное значение. Она бывает маленькая и большая. Медленно движется черепаха, но быстро бежит гепард.

Получается, у скорости есть численное значение и направление. Такие величины называются векторными (просто векторами).

Обозначается векторная величина стрелкой над буквой, например, . Численное значение векторной величины записывается с двумя вертикальными палочками и называется модулем вектора. Например, модуль вектора скорости автобуса | | = 70 км/ч. Зная модуль вектора скорости, можно вычислить какой путь автобус прошел от остановки, а при известном направлении вектора (т.е. в какую сторону от остановки) уже определяется местоположением автобуса.                          

Величины, не имеющие направления, называются скалярами. Примеры скалярных величин: температура, время, объем, площадь, длина.

Вектор изображают в виде направленного отрезка, т. е. имеющего начало и конец. Конец отрезка отмечают стрелкой.

Основные свойства векторов

Два или несколько векторов с одинаковым модулем и направлением и равны.

• Векторы, различающиеся по направлению не равны, если даже равны их численные значения.

• Сумма одинаково направленных векторов по модулю равна сумме модулей этих векторов и имеет то же направление.

По этому правилу находят скорость по течению. Теплоход имеет собственную скорость, которую могут создать двигатели теплохода. У течения реки есть своя скорость. При движении по течению река будто помогает теплоходу. Скорости складываются. Числовой результат получается больше. Например, собственная скорость теплохода 60 км/ч, а скорость течения реки 2 км/ч. Результирующая скорость по модулю равна 62 км/ч, а направление остается тем же.

• Если векторы направлены в противоположные стороны, то результирующий вектор направлен в сторону большего из них, а его численное значение равно разности численных значений этих векторов.

По этому правилу находят скорость против течения. При движении против течения река будто мешает движению теплохода, толкает течением назад. Значит, из модуля скорости теплохода надо вычесть модуль скорости течения. Здесь важно, чтобы вектор собственной скорости был больше, чем вектор скорости течения, иначе теплоход будет двигаться назад, даже при постоянной работе двигателей. Например, теплоход с собственной скоростью 60 км/ч движется в обратном направлении против течения реки, скорость которой 2 км/ч. Теплоход в результате будет иметь численное значение скорости 58 км/ч, направление вектора скорости – против течения.

• Векторы можно умножать, делить, складывать. Как это делается, изучают на уроках математики.

Физикой свойства векторов используются при изучении величин, имеющих модуль и направление. Первой из них и является скорость.

Основная задача механики

Это строки из замечательного произведения Марка Твена «Приключения Тома Сойера»

Том целый день копался в земле то у дерева, то на холме, но клада так и не нашел. Прежде, чем отправиться за кладом, надо знать, где он находится.

Умение найти положение любого тела в данный момент времени и есть основная задача механики. Эту задачу решают диспетчеры, отправляющие поезд в путь. Они должны знать, как двигаются поезда, иначе – авария. Отправляя самолет в рейс, ракету в полет, специальные службы просчитывают траектории их движения. Космический корабль в огромных просторах космоса должен встретиться и состыковаться со станцией. Для этого надо произвести точнейшие расчеты, чтобы избежать ошибок, приводящих к неудаче.

Почему Том Сойер не мог решить основную задачу механики? Чтобы определить положение тела, надо знать еще какое-то тело, от которого вести отсчет расстояния, и направление, куда это расстояние отмерять. Герои «Острова сокровищ» (автор книги Роберт Стивенсон) смогли найти место, где лежал клад, так как у них была информация о направлении поиска и о дереве, от которого надо вести отсчет расстояния.

Так было написано на карте, которая вела к кладу на острове Сокровищ.

Стоит разобраться в записке на карте. Итак, высокое дерево – это тело, от которого надо вести отсчет расстояния в указанном направлении. Дано и расстояние — «в десяти саженях». Основная задача механики здесь решается.

Чтобы определить, где находится тело на прямой, на плоскости, в пространстве, нужно знать:

Если соединить по прямой тело отсчета с местом, где оказалось движущееся тело, получится отрезок, имеющий длину и направление (в сторону от тела отсчета до нового положения). Этот отрезок называется перемещением. Для обозначения используется буква s, но в отличие от пройденного пути над буквой ставится стрелка, так как перемещение есть векторная величина. Пройденный путь – это скаляр, он имеет только длину.

Итак, перемещение  — это вектор, соединяющий начальное и конечное положение тела.

(Источник)

Имея тело отсчета и перемещение, легко можно справиться с основной задачей механики.

При движении тела по прямой численные значения перемещения и пройденного пути совпадают и находятся по формуле s = v ∙ t. А если движение криволинейно? Вот три различных примера.

1. На соревнованиях по ориентированию, двигаясь от старта строго по компасу на северо-восток, Миша прошел 670 м. В этом случае 670м – это и пройденный мальчиком путь, и модуль вектора перемещения, направление которого задано.
2. Дима с Сережей отправились в лес за грибами. В лес они зашли от столба с пометкой 5 км. Набрав по корзинке грибов, друзья через 2 ч вышли на шоссе у столба с пометкой 6 км. Разве ребята прошагали по лесу 1 км? В этом случае перемещение мальчиков направлено от первого столба ко второму и по модулю равно 1 км. А вот пройденный путь, который прошли мальчики за 2 ч, двигаясь по сложной траектории, составляет несколько километров.
3. Братья Чук и Гек после прогулки вернулись домой. Начало совпадает с концом пути. Перемещение братьев получается равным нулю. За время прогулки дети прошли несколько метров, значит пройденный путь, в отличие от перемещения, нулю не равен.

Итак:

Механическое движение – это изменение положения тела в пространстве относительно других тел.

Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся. В этом проявляется относительность механического движения. Далее кратко рассмотрим основные виды механического движения.

Поступательное движение – это движение тела, при котором все его точки движутся одинаково.

Например, всё тот же автомобиль совершает по дороге поступательное движение. Точнее, поступательное движение совершает только кузов автомобиля, в то время как его колёса совершают вращательное движение.

Вращательное движение – это движение тела вокруг некоторой оси. При таком движении все точки тела совершают движение по окружностям, центром которых является эта ось.

Упоминавшиеся нами колёса совершают вращательное движение вокруг своих осей, и в то же время колёса совершают поступательное движение вместе с кузовом автомобиля. То есть относительно оси колесо совершает вращательное движение, а относительно дороги – поступательное.

Колебательное движение – это периодическое движение, которое совершается поочерёдно в двух противоположных направлениях.

Например, колебательное движение совершает маятник в часах.

Поступательное и вращательное движения – самые простые виды механического движения.

Относительность механического движения

Все тела во Вселенной движутся, поэтому не существует тел, которые находятся в абсолютном покое. По той же причине определить движется тело или нет, можно только относительно какого-либо другого тела.

Например, автомобиль движется по дороге. Дорога находится на планете Земля. Дорога неподвижна. Поэтому можно измерить скорость автомобиля относительно неподвижной дороги. Но дорога неподвижна относительно Земли. Однако сама Земля вращается вокруг Солнца. Следовательно, дорога вместе с автомобилем также вращается вокруг Солнца. Следовательно, автомобиль совершает не только поступательное движение, но и вращательное (относительно Солнца). А вот относительно Земли автомобиль совершает только поступательное движение. В этом проявляется относительность механического движения.

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.

Материальная точка

Во многих случаях размером тела можно пренебречь, так как размеры этого тела малы по сравнению с расстоянием, которое походит это тело, или по сравнению с расстоянием между этим телом и другими телами. Такое тело для упрощения расчетов условно можно считать материальной точкой, имеющей массу этого тела.

Материальная точка – это тело, размерами которого в данных условиях можно пренебречь.

Многократно упоминавшийся нами автомобиль можно принять за материальную точку относительно Земли. Но если человек перемещается внутри этого автомобиля, то пренебрегать размерами автомобиля уже нельзя.

Как правило, решая задачи по физике, рассматривают движение тела как движение материальной точки, и оперируют такими понятиями, как скорость материальной точки, ускорение материальной точки, импульс материальной точки, инерция материальной точки и т.п.

Система отсчёта

Материальная точка движется относительно других тел. Тело, по отношению к которому рассматривается данное механическое движение, называется телом отсчёта. Тело отсчёта выбирают произвольно в зависимости от решаемых задач.

С телом отсчёта связывается система координат, которая представляет из себя точку отсчёта (начало координат). Система координат имеет 1, 2 или 3 оси в зависимости от условий движения. Положение точки на линии (1 ось), плоскости (2 оси) или в пространстве (3 оси) определяют соответственно одной, двумя или тремя координатами. Для определения положения тела в пространстве в любой момент времени также необходимо задать начало отсчёта времени.

Система отсчёта – это система координат, тело отсчета, с которым связана система координат, и прибор для измерения времени. Относительно системы отсчёта и рассматривается движение тела. У одного и того же тела относительно разных тел отсчёта в разных системах координат могут быть совершенно различные координаты.

Траектория движения также зависит от выбора системы отсчёта.

Виды систем отсчёта могут быть различными, например, неподвижная система отсчёта, подвижная система отсчёта, инерциальная система отсчёта, неинерциальная система отсчёта.

Механическое движение.

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: механическое движение и его виды, относительность механического движения, скорость, ускорение.

Понятие движения является чрезвычайно общим и охватывает самый широкий круг явлений. В физике изучают различные виды движения. Простейшим из них является механическое движение. Оно изучается в механике.
Механическое движение — это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.

Если тело A меняет своё положение относительно тела B, то и тело B меняет своё положение относительно тела A. Иначе говоря, если тело A движется относительно тела B, то и тело B движется относительно тела A. Механическое движение является относительным — для описания движения необходимо указать, относительно какого тела оно рассматривается.

Так, например, можно говорить о движении поезда относительно земли, пассажира относительно поезда, мухи относительно пассажира и т. д. Понятия абсолютного движения и абсолютного покоя не имеют смысла: пассажир, покоящийся относительно поезда, будет двигаться с ним относительно столба на дороге, совершать вместе с Землёй суточное вращение и двигаться вокруг Солнца.
Тело, относительно которого рассматривается движение, называется телом отсчёта.

Основной задачей механики является определение положения движущегося тела в любой момент времени. Для решения этой задачи удобно представить движение тела как изменение координат его точек с течением времени. Чтобы измерить координаты, нужна система координат. Чтобы измерять время, нужны часы. Всё это вместе образует систему отсчёта.

Система отсчёта — это тело отсчёта вместе с жёстко связанной с ним («вмороженной»» в него) системой координат и часами.
Система отсчёта показана на рис. 1. Движение точки рассматривается в системе координат . Начало координат является телом отсчёта.

Рисунок 1.

Вектор называется радиус-вектором точки . Координаты точки являются в то же время координатами её радиус-вектора .
Решение основной задачи механики для точки состоит в нахождении её координат как функций времени: .
В ряде случаев можно отвлечься от формы и размеров изучаемого объекта и рассматривать его просто как движущуюся точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях данной задачи.
Так, поезд можно считать материальной точкой при его движении из Москвы в Саратов, но не при посадке в него пассажиров. Землю можно считать материальной точкой при описании её движения вокруг Солнца, но не её суточного вращения вокруг собственной оси.

К характеристикам механического движения относятся траектория, путь, перемещение, скoрость и ускорение.

Траектория, путь, перемещение.

В дальнейшем, говоря о движущемся (или покоящемся) теле, мы всегда полагаем, что тело можно принять за материальную точку. Случаи, когда идеализацией материальной точки пользоваться нельзя, будут специально оговариваться.

Траектория — это линия, вдоль которой движется тело. На рис. 1 траекторией точки является синяя дуга, которую описывает в пространстве конец радиус-вектора .
Путь — это длина участка траектории, пройденного телом за данный промежуток времени.
Перемещение — это вектор, соединяющий начальное и конечное положение тела.
Предположим, что тело начало движение в точке и закончило движение в точке (рис. 2). Тогда путь, пройденный телом, это длина траектории . Перемещение тела — это вектор .

Рисунок 2.

Скорость и ускорение.

Рассмотрим движение тела в прямоугольной системе координат с базисом (рис. 3).

Рисунок 3.

Пусть в момент времени тело находилось в точке с радиус-вектором

Спустя малый промежуток времени тело оказалось в точке с
радиус-вектором

Перемещение тела:

(1)

Мгновенная скорость в момент времени — это предел отношения перемещения к интервалу времени , когда величина этого интервала стремится к нулю; иными словами, скорость точки — это производная её радиус-вектора:

(2)

Из (2) и (1) получаем:

Коэффициенты при базисных векторах в пределе дают производные:

(Производная по времени традиционно обозначается точкой над буквой.) Итак,

Мы видим, что проекции вектора скорости на координатные оси являются производными координат точки:

Когда стремится к нулю, точка приближается к точке и вектор перемещения разворачивается в направлении касательной. Оказывается, что в пределе вектор направлен точно по касательной к траектории в точке . Это и показано на рис. 3.

Понятие ускорения вводится похожит образом. Пусть в момент времени скорость тела равна , а спустя малый интервал скорость стала равна .
Ускорение — это предел отношения изменения скорости к интервалу , когда этот интервал стремится к нулю; иначе говоря, ускорение — это производная скорости:

Ускорение, таким образом, есть «cкорость изменения скорости». Имеем:

Следовательно, проекции ускорения являются производными проекций скорости (и, стало быть, вторыми производными координат):

Закон сложения скоростей.

Пусть имеются две системы отсчёта. Одна из них связана с неподвижным телом отсчёта . Эту систему отсчёта обозначим и будем называть неподвижной.
Вторая система отсчёта, обозначаемая , связана с телом отсчёта , которое движется относительно тела со скоростью . Эту систему отсчёта называем движущейся. Дополнительно предполагаем, что координатные оси системы перемещаются параллельно самим себе (нет вращения системы координат), так что вектор можно считать скоростью движущейся системы относительно неподвижной.

Неподвижная система отсчёта обычно связана с землёй. Если поезд плавно едет по рельсам со скоростью , это система отсчёта, связанная с вагоном поезда, будет движущейся системой отсчёта .

Заметим, что скорость любой точки вагона (кроме вращающихся колёс!) равна . Если муха неподвижно сидит в некоторой точке вагона, то относительно земли муха движется со скоростью . Муха переносится вагоном, и потому скорость движущейся системы относительно неподвижной называется переносной скоростью.

Предположим теперь, что муха поползла по вагону. Скорость мухи относительно вагона (то есть в движущейся системе ) обозначается и называется относительной скоростью. Скорость мухи относительно земли (то есть в неподвижной системе ) обозначается и называется абсолютной скоростью.

Выясним, как связаны друг с другом эти три скорости — абсолютная, относительная и переносная.
На рис. 4 муха обозначена точкой .Далее:
— радиус-вектор точки в неподвижной системе ;
— радиус-вектор точки в движущейся системе ;
— радиус-вектор тела отсчёта в неподвижной системе .

Рисунок 4.

Как видно из рисунка,

Дифференцируя это равенство, получим:

(3)

(производная суммы равна сумме производных не только для случая скалярных функций, но и для векторов тоже).
Производная есть скорость точки в системе , то есть абсолютная скорость:

.

Аналогично, производная есть скорость точки в системе , то есть относительная скорость:

А что такое ? Это скорость точки в неподвижной системе, то есть — переносная скорость движущейся системы относительно неподвижной:

В результате из (3) получаем:

Закон сложения скоростей. Скорость точки относительно неподвижной системы отсчёта равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы. Иными словами, абсолютная скорость есть сумма переносной и относительной скоростей.

Таким образом, если муха ползёт по движущемуся вагону, то скорость мухи относительно земли равна векторной сумме скорости вагона и скорости мухи относительно вагона. Интуитивно очевидный результат!

Виды механического движения.

Простейшими видами механического движения материальной точки являются равномерное и прямолинейное движения.
Движение называется равномерным, если модуль вектора скорости остаётся постоянным (направление скорости при этом может меняться).

Движение называется прямолинейным, если направление вектора скорости остаётся постоянным (а величина скорости при этом может меняться). Траекторией прямолинейного движения служит прямая линия, на которой лежит вектор скорости.
Например, автомобиль, который едет с постоянной скоростью по извилистой дороге, совершает равномерное (но не прямолинейное) движение. Автомобиль, разгоняющийся на прямом участке шоссе, совершает прямолинейное (но не равномерное) движение.

А вот если при движении тела остаются постоянными как модуль скорости, так и его направление, то движение называется равномерным прямолинейным.

В терминах вектора скорости можно дать более короткие определения данным типам движения:

Важнейшим частным случаем неравномерного движения является равноускоренное движение, при котором остаются постоянными модуль и направление вектора ускорения:

• равноускоренное движение

Наряду с материальной точкой в механике рассматривается ещё одна идеализация — твёрдое тело.
Твёрдое тело — это система материальных точек, расстояния между которыми не меняются со временем. Модель твёрдого тела применяется в тех случаях, когда мы не можем пренебречь размерами тела, но можем не принимать во внимание изменение размеров и формы тела в процессе движения.

Простейшими видами механического движения твёрдого тела являются поступательное и вращательное движения.
Движение тела называется поступательным, если всякая прямая, соединяющая две какие-либо точки тела, перемещается параллельно своему первоначальному направлению. При поступательном движении траектории всех точек тела идентичны: они получаются друг из друга параллельным сдвигом (рис. 5).

Рисунок 5.

Движение тела называется вращательным, если все его точки описывают окружности, лежащие в параллельных плоскостях. При этом центры данных окружностей лежат на одной прямой, которая перпендикулярна всем этим плоскостям и называется осью вращения.

На рис. 6 изображён шар, вращающийся вокруг вертикальной оси. Так обычно рисуют земной шар в соответствующих задачах динамики.

Рисунок 6.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн