Виленкин рассказы о множествах

Н. Я. Виленкин

Рассказы о множествах

3-е издание

1В настоящее время — академик РАН. — Прим. ред.

1Список литературы обновлён. — Прим. ред.

Глава I. Множества и действия над ними

Что такое множество

В этой главе будет рассказано о том, что такое множества и какие действия можно выполнять над ними. К сожалению, основному понятию теории — понятию множества — нельзя дать строгого определения. Разумеется, можно сказать, что множество — это «совокупность», «собрание», «ансамбль», «коллекция», «семейство», «система», «класс» и т. д. Однако все это было бы не математическим определением, а скорее злоупотреблением словарным богатством русского языка.

Для того чтобы определить какое-либо понятие, нужно прежде всего указать, частным случаем какого более общего понятия оно является. Для понятия множества сделать это невозможно, потому что более общего понятия, чем множество, в математике нет.

Поэтому вместо того, чтобы дать определение понятию множества, мы проиллюстрируем его на примерах.

Часто приходится говорить о нескольких вещах, объединенных некоторым общим признаком. Так, можно говорить о множестве всех стульев в комнате, о множестве всех атомов на Юпитере, о множестве всех клеток человеческого тела, о множестве всех картофелин в данном мешке, о множестве всех рыб в океане, о множестве всех квадратов на плоскости, о множестве всех точек на данной окружности и т. д.

Предметы, составляющие данное множество, называются его элементами. Для того чтобы указать, что данное множество A состоит из элементов x, y, …, z, обычно пишут

A = {x, y, …, z}.

Например, множество дней недели состоит из элементов {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}, множество месяцев — из элементов {январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь}, множество

Возможны различные способы задания множества. Один из них состоит в том, что дается полный список элементов, входящих в множество. Например, множество учеников данного класса

определяется их списком в классном журнале, множество всех стран на земном шаре — их списком в географическом атласе, множество всех костей в человеческом скелете — их списком в учебнике анатомии.

Великая перепись рыб

Но этот способ применим только к конечным множествам, да

ито далеко не ко всем. Например, хотя множество всех рыб в океане

иконечно, вряд ли его можно задать списком. А уж бесконечные множества никак нельзя определять с помощью списка; попробуйте, например, составить список всех натуральных чисел или список всех точек окружности — ясно, что составление этого списка никогда не закончится.

Втех случаях, когда множество нельзя задать при помощи списка, его задают путем указания некоторого характеристического свойства — такого свойства, что элементы множества им обладают, а все остальное на свете не обладает. Например, мы можем говорить о множестве всех натуральных чисел. Тогда ясно, что число 73 принад-

лежит этому множеству, а число 3 или крокодил не принадлежат.

√ 4

Точно так же 2 и планета Сатурн не принадлежат множеству всех рациональных чисел, а 157 принадлежит этому множеству.

8Глава I. Множества и действия над ними

Вгеометрии часто приходится иметь дело с множествами точек, заданными теми или иными характеристическими свойствами. Обычно, следуя древним традициям, множество точек с данным характеристическим свойством в геометрии называют геометрическим местом точек. Например, говорят так: «Окружностью называется геометрическое место точек плоскости, равноудаленных от данной точки этой плоскости». Это означает, что множество точек плоскости, равноудаленных от данной точки этой плоскости, совпадает с множеством точек некоторой окружности.

Крокодил не входит в множество натуральных чисел

Задание множеств их характеристическими свойствами иногда приводит к осложнениям. Может случиться, что два различных характеристических свойства задают одно и то же множество, то есть всякий элемент, обладающий одним свойством, обладает и другим, и обратно. Например, множество толстокожих сухопутных животных, имеющих два бивня, совпадает с множеством толстокожих животных, имеющих хобот, — это множество слонов.

В геометрии свойство «точка M равноудалена от сторон угла AOB» задает то же точечное множество, что и свойство «угол AOM равен углу MOB» (здесь рассматриваются точки плоскости, лежащие внутри угла AOB, см. рис. 1). А в арифметике свойство «целое число делится на 2» задает то же множество, что и свойство «последняя цифра целого числа делится на 2».

Иногда бывает трудно доказать равносильность двух характеристических свойств. Попробуйте, например, доказать, что следующие свойства задают одно и то же множество точек, лежащих в одной плоскости с треугольником ABC:

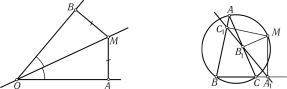
а) основания перпендикуляров, опущенных из точки M на стороны треугольника ABC, лежат на одной прямой;

б) точка M лежит на окружности, описанной вокруг треугольника ABC (рис. 2).

(Совпадение этих множеств составляет содержание так называемой теоремы Симсона и теоремы, обратной ей.)

Вообще, во многих математических теоремах речь идет о совпадении двух множеств, например множества равносторонних треугольников с множеством равноугольных треугольников, множества описанных четырехугольников с множеством четырехугольников, суммы противоположных сторон которых равны, и т. д. В некоторых случаях проблема совпадения или различия двух множеств, заданных своими характеристическими свойствами, не решена до сих пор. Так, до сих пор неизвестно, совпадает ли множество {1093, 3511} с множеством простых чисел n, для которых 2n − 2 делится на n2.

Еще большие трудности при задании множеств их характеристическими свойствами возникают из-за недостаточной четкости обыденного языка, неоднозначности человеческой речи. Большое число промежуточных форм затрудняет разграничение объектов на принадлежащие и не принадлежащие данному множеству. Пусть, например, речь идет о множестве всех деревьев на земном шаре. В первую очередь здесь надо определить, идет ли речь обо всех деревьях, которые существовали и будут существовать на Земле, или о деревьях, существовавших в течение некоторого фиксированного промежутка времени (например, с 1 мая по 1 сентября 1965 года). Но тогда возникает вопрос, как быть с деревьями, спиленными за этот промежуток времени? Кроме того, существует целый ряд промежуточных форм между деревьями и другими растениями, и надо решить, какие из них относятся к множеству деревьев, а какие нет.

Даже множество планет Солнечной системы определено не вполне однозначно. Наряду с большими планетами (Меркурием, Венерой,

Н. Я. Виленкин

Рассказы о множествах

3-е издание

МЦНМО

2005

УДК 510.2
ББК 22.12

В44

Виленкин Н. Я.

В44

Рассказы о множествах. 3-е издание. — М.: МЦНМО,

2005. — 150 с.

ISBN 5-94057-036-4

В 70-х годах XIX века немецкий математик Г. Кантор создал

новую область математики — теорию бесконечных множеств. Че-
рез несколько десятилетий почти вся математика была перестрое-
на на теоретико-множественной основе. Понятия теории множеств
отражают наиболее общие свойства математических объектов.

Обычно теорию множеств излагают в учебниках для универ-

ситетов. В настоящей книге в популярной форме описываются
основные понятия и результаты теории множеств.

Книга предназначена для учащихся старших классов средней

школы, интересующихся математикой, а также для широких кру-
гов читателей, желающих узнать, что такое теория множеств.

ББК 22.12

Виленкин Наум Яковлевич

РАССКАЗЫ О МНОЖЕСТВАХ

Дизайн обложки Соповой У. В.

Издательство Московского центра непрерывного математического образования.
119002, Москва, Большой Власьевский пер., 11.

Лицензия ИД № 01335 от 24.03.2000 г.

Подписано к печати 03.11.2003 г.

Формат

60

×

88

/

16

. Печать офсетная. Объем 9.5 печ. л. Доп. тираж 2000 экз.

Заказ №

.

Отпечатано с готовых диапозитивов в ФГУП «Полиграфические ресурсы».

ISBN 5-94057-036-4

c

Виленкин А. Н., 2005.

c

МЦНМО, 2005.

Предисловие ко второму изданию

О теории множеств мне довелось услышать, когда я учился

в восьмом классе. Однажды я попал на лекцию, которую прочел
для московских школьников И. М. Гельфанд — тогда начинающий
доцент, а ныне член-корреспондент АН СССР

1

. В течение двух

часов он рассказывал нам о совершенно невероятных вещах: что
натуральных чисел столько же, сколько и четных, рациональных
столько же, сколько и натуральных, а точек на отрезке столько же,
сколько и в квадрате.

Знакомство с теорией множеств было продолжено в годы обуче-

ния на механико-математическом факультете МГУ. Наряду с лекци-
ями и семинарами там существовал своеобразный метод обучения,
о котором, возможно, и не подозревали профессора и доценты. После
занятий (а иногда — что уж греха таить — и во время не слиш-
ком интересных лекций) студенты бродили по коридорам старого
здания на Моховой и обсуждали друг с другом интересные зада-
чи, неожиданные примеры и остроумные доказательства. Именно
в этих разговорах студенты-первокурсники узнавали от своих стар-
ших товарищей, как строить кривую, проходящую через все точки
квадрата, или функцию, не имеющую нигде производной, и т. д.

Разумеется, объяснения давались, как говорится, «на пальцах»,

и идти сдавать экзамен, прослушав эти объяснения, было бы непро-
стительным легкомыслием. Но ведь об экзамене не было и речи —
по учебному плану курс теории функций действительного перемен-
ного надо было сдавать еще через два года. Но как же потом, при
слушании лекций и сдаче экзаменов, помогала «коридорная» подго-
товка! По поводу каждой теоремы вспоминались интересные задачи,
которые приходилось решать раньше, остроумные сравнения, на-
глядные образы.

Мне захотелось рассказать читателю о теории множеств пример-

но в том же стиле, в каком я сам изучал ее, проходя «коридор-
ный» курс обучения. Поэтому основное внимание будет обращено
на то, чтобы сделать ясной постановку задач, рассказать о неожи-
данных и удивительных примерах, сплошь и рядом противоречащих

1

В настоящее время — академик РАН. —

Прим. ред.

4

Предисловие ко второму изданию

наивному представлению, которыми так богата теория функций дей-
ствительного переменного. И если, прочтя эту книгу, школьник стар-
ших классов или студент первых курсов университета или пединсти-
тута почувствует желание более глубоко изучить теорию множеств,
теорию функций действительного переменного, автор будет считать,
что его цель достигнута.

∗ ∗ ∗

Из серьезных курсов можно было бы рекомендовать следующие:

1

1.

Александров П

.

С

. Введение в теорию множеств и функций,

Гостехиздат, 1948.

2.

Колмогоров А

.

Н

.,

Фомин С

.

В

. Элементы теории функций

и функционального анализа, Изд-во МГУ, ч. 1, 1954, ч. 2, 1960;
Наука, 1981.

3.

Лузин Н

.

Н

. Теория функций действительного переменного,

Учпедгиз, 1948.

4.

Натансон И

.

П

. Теория функций вещественной переменной,

Гостехиздат, 1950; Наука, 1974.

5.

Хаусдорф Ф

. Теория множеств, ОНТИ, 1937.

6.

Куратовский К

.,

Мостовский А

. Теория множеств, «Мир»,

1970.

Много интересных задач по теории множеств собрано в книге

Ю. С. Очана «Сборник задач и теорем по теории функций действи-
тельного переменного» («Просвещение», 1965).

По некоторым вопросам, затронутым здесь, много интересных

сведений содержится в книге А. С. Пархоменко «Что такое линия»
(ГИТТЛ, 1954). В конце книги приведен ряд задач по теории функ-
ций действительного переменного, решение которых будет полезно
читателю. Отметим еще, что некоторые более трудные места можно
при первом чтении пропустить без ущерба для понимания дальней-
шего. Эти места мы отметили звездочками.

1

Список литературы обновлён. —

Прим. ред.

Н. Я. Виленкин
Рассказы о множествах
3-е издание
МЦНМО
2005

УДК 510.2
ББК 22.12
В44
Виленкин Н. Я.
В44
Рассказы о множествах. 3-е издание. — М.: МЦНМО,
2005. — 150 с.
ISBN 5-94057-036-4
В 70-х годах XIX века немецкий математик Г. Кантор создал новую область математики — теорию бесконечных множеств. Че- рез несколько десятилетий почти вся математика была перестрое- на на теоретико-множественной основе. Понятия теории множеств отражают наиболее общие свойства математических объектов.
Обычно теорию множеств излагают в учебниках для универ- ситетов. В настоящей книге в популярной форме описываются основные понятия и результаты теории множеств.
Книга предназначена для учащихся старших классов средней школы, интересующихся математикой, а также для широких кру- гов читателей, желающих узнать, что такое теория множеств.
ББК 22.12
Виленкин Наум Яковлевич
РАССКАЗЫ О МНОЖЕСТВАХ
Дизайн обложки Соповой У. В.
Издательство Московского центра непрерывного математического образования.
119002, Москва, Большой Власьевский пер., 11.
Лицензия ИД № 01335 от 24.03.2000 г.
Подписано к печати 03.11.2003 г.
Формат 60 × 88/16. Печать офсетная. Объем 9.5 печ. л. Доп. тираж 2000 экз.
Заказ №
Отпечатано с готовых диапозитивов в ФГУП «Полиграфические ресурсы».
ISBN 5-94057-036-4
c Виленкин А. Н., 2005.
c МЦНМО, 2005.

Предисловие ко второму изданию
О теории множеств мне довелось услышать, когда я учился в восьмом классе. Однажды я попал на лекцию, которую прочел для московских школьников И. М. Гельфанд — тогда начинающий доцент, а ныне член-корреспондент АН СССР
1
. В течение двух часов он рассказывал нам о совершенно невероятных вещах: что натуральных чисел столько же, сколько и четных, рациональных столько же, сколько и натуральных, а точек на отрезке столько же,
сколько и в квадрате.
Знакомство с теорией множеств было продолжено в годы обуче- ния на механико-математическом факультете МГУ. Наряду с лекци- ями и семинарами там существовал своеобразный метод обучения,
о котором, возможно, и не подозревали профессора и доценты. После занятий (а иногда — что уж греха таить — и во время не слиш- ком интересных лекций) студенты бродили по коридорам старого здания на Моховой и обсуждали друг с другом интересные зада- чи, неожиданные примеры и остроумные доказательства. Именно в этих разговорах студенты-первокурсники узнавали от своих стар- ших товарищей, как строить кривую, проходящую через все точки квадрата, или функцию, не имеющую нигде производной, и т. д.
Разумеется, объяснения давались, как говорится, «на пальцах»,
и идти сдавать экзамен, прослушав эти объяснения, было бы непро- стительным легкомыслием. Но ведь об экзамене не было и речи —
по учебному плану курс теории функций действительного перемен- ного надо было сдавать еще через два года. Но как же потом, при слушании лекций и сдаче экзаменов, помогала «коридорная» подго- товка! По поводу каждой теоремы вспоминались интересные задачи,
которые приходилось решать раньше, остроумные сравнения, на- глядные образы.
Мне захотелось рассказать читателю о теории множеств пример- но в том же стиле, в каком я сам изучал ее, проходя «коридор- ный» курс обучения. Поэтому основное внимание будет обращено на то, чтобы сделать ясной постановку задач, рассказать о неожи- данных и удивительных примерах, сплошь и рядом противоречащих
1
В настоящее время — академик РАН. — Прим. ред.

4
Предисловие ко второму изданию наивному представлению, которыми так богата теория функций дей- ствительного переменного. И если, прочтя эту книгу, школьник стар- ших классов или студент первых курсов университета или пединсти- тута почувствует желание более глубоко изучить теорию множеств,
теорию функций действительного переменного, автор будет считать,
что его цель достигнута.
∗ ∗ ∗
Из серьезных курсов можно было бы рекомендовать следующие:
1 1. Александров П. С. Введение в теорию множеств и функций,
Гостехиздат, 1948.
2. Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа, Изд-во МГУ, ч. 1, 1954, ч. 2, 1960;
Наука, 1981.
3. Лузин Н. Н. Теория функций действительного переменного,
Учпедгиз, 1948.
4. Натансон И. П. Теория функций вещественной переменной,
Гостехиздат, 1950; Наука, 1974.
5. Хаусдорф Ф. Теория множеств, ОНТИ, 1937.
6. Куратовский К., Мостовский А. Теория множеств, «Мир»,
1970.
Много интересных задач по теории множеств собрано в книге
Ю. С. Очана «Сборник задач и теорем по теории функций действи- тельного переменного» («Просвещение», 1965).
По некоторым вопросам, затронутым здесь, много интересных сведений содержится в книге А. С. Пархоменко «Что такое линия»
(ГИТТЛ, 1954). В конце книги приведен ряд задач по теории функ- ций действительного переменного, решение которых будет полезно читателю. Отметим еще, что некоторые более трудные места можно при первом чтении пропустить без ущерба для понимания дальней- шего. Эти места мы отметили звездочками.
1
Список литературы обновлён. — Прим. ред.

Глава I. Множества и действия над ними
Что такое множество
В этой главе будет рассказано о том, что такое множества и ка- кие действия можно выполнять над ними. К сожалению, основно- му понятию теории — понятию множества — нельзя дать строго- го определения. Разумеется, можно сказать, что множество — это
«совокупность», «собрание», «ансамбль», «коллекция», «семейство»,
«система», «класс» и т. д. Однако все это было бы не математиче- ским определением, а скорее злоупотреблением словарным богат- ством русского языка.
Для того чтобы определить какое-либо понятие, нужно прежде всего указать, частным случаем какого более общего понятия оно является. Для понятия множества сделать это невозможно, потому что более общего понятия, чем множество, в математике нет.
Поэтому вместо того, чтобы дать определение понятию множе- ства, мы проиллюстрируем его на примерах.
Часто приходится говорить о нескольких вещах, объединенных некоторым общим признаком. Так, можно говорить о множестве всех стульев в комнате, о множестве всех атомов на Юпитере, о множе- стве всех клеток человеческого тела, о множестве всех картофелин в данном мешке, о множестве всех рыб в океане, о множестве всех квадратов на плоскости, о множестве всех точек на данной окруж- ности и т. д.
Предметы, составляющие данное множество, называются его эле- ментами. Для того чтобы указать, что данное множество A состоит из элементов x, y, . . . , z, обычно пишут
A = {x, y, . . . , z}.
Например, множество дней недели состоит из элементов {понедель- ник, вторник, среда, четверг, пятница, суббота, воскресенье}, множе- ство месяцев — из элементов {январь, февраль, март, апрель, май,
июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь}, множество

6
Глава I. Множества и действия над ними арифметических действий — из элементов {сложение, вычитание,
умножение, деление}, а множество корней квадратного уравнения x
2
− 2x − 24 = 0 — из двух чисел: −4 и 6, то есть имеет вид {−4, 6}.
Фигурные скобки в обозначении множества показывают, что эле- менты объединены в одно целое — множество A. Тот факт, что эле- мент x принадлежит множеству A, записывают с помощью знака ∈
так: x ∈ A. Если же данный элемент x не принадлежит множеству A,
то пишут x ∈ A. Например, если A означает множество всех четных натуральных чисел, то 6 ∈ A, а 3 ∈ A. Если A — множество всех ме- сяцев в году, то май ∈ A, а среда ∈ A.
Таким образом, когда мы говорим о множестве, то объединяем некоторые предметы в одно целое, а именно в множество, элемен- тами которого они являются. Основатель теории множеств Георг
Кантор подчеркнул это следующими словами: «Множество есть многое, мыслимое нами как единое». Собственно говоря, элемен- ты множества могут и не быть реально существующими предмета- ми — в богословских трактатах всерьез изучаются взаимоотношения в множествах архангелов, злых духов и т. д.
Для того чтобы наглядно представить себе понятие множества,
академик Н. Н. Лузин предложил следующий образ. Представим прозрачную непроницаемую оболочку, нечто вроде плотно закры- того прозрачного мешка. Предположим, что внутри этой оболочки заключены все элементы данного множества A, и что кроме них внутри оболочки никаких других предметов не находится. Эта обо- лочка с предметами x, находящимися внутри нее, и может служить образом множества A, составленного из элементов x. Сама же эта прозрачная оболочка, охватывающая все элементы (и ничего дру- гого кроме них), довольно хорошо изображает тот акт объединения элементов x, в результате которого создается множество A.
Если множество содержит конечное число элементов, то его на- зывают конечным, а если в нем бесконечно много элементов, то бес- конечным. Так, множество деревьев в лесу конечно, а множество точек на окружности бесконечно.
Как задают множества
Возможны различные способы задания множества. Один из них состоит в том, что дается полный список элементов, входящих в множество. Например, множество учеников данного класса

Как задают множества
7
определяется их списком в классном журнале, множество всех стран на земном шаре — их списком в географическом атласе, мно- жество всех костей в человеческом скелете — их списком в учебнике анатомии.
Великая перепись рыб
Но этот способ применим только к конечным множествам, да и то далеко не ко всем. Например, хотя множество всех рыб в океане и конечно, вряд ли его можно задать списком. А уж бесконечные множества никак нельзя определять с помощью списка; попробуй- те, например, составить список всех натуральных чисел или список всех точек окружности — ясно, что составление этого списка никогда не закончится.
В тех случаях, когда множество нельзя задать при помощи спис- ка, его задают путем указания некоторого характеристического свой- ства — такого свойства, что элементы множества им обладают, а все остальное на свете не обладает. Например, мы можем говорить о мно- жестве всех натуральных чисел. Тогда ясно, что число 73 принад- лежит этому множеству, а число
3 4
или крокодил не принадлежат.
Точно так же
√
2 и планета Сатурн не принадлежат множеству всех рациональных чисел, а
7 15
принадлежит этому множеству.

8
Глава I. Множества и действия над ними
В геометрии часто приходится иметь дело с множествами то- чек, заданными теми или иными характеристическими свойствами.
Обычно, следуя древним традициям, множество точек с данным характеристическим свойством в геометрии называют геометри- ческим местом точек. Например, говорят так: «Окружностью называется геометрическое место точек плоскости, равноудаленных от данной точки этой плоскости». Это означает, что множество точек плоскости, равноудаленных от данной точки этой плоскости,
совпадает с множеством точек некоторой окружности.
Крокодил не входит в множество натуральных чисел
Задание множеств их характеристическими свойствами иногда приводит к осложнениям. Может случиться, что два различных ха- рактеристических свойства задают одно и то же множество, то есть всякий элемент, обладающий одним свойством, обладает и другим,
и обратно. Например, множество толстокожих сухопутных живот- ных, имеющих два бивня, совпадает с множеством толстокожих жи- вотных, имеющих хобот, — это множество слонов.
В геометрии свойство «точка M равноудалена от сторон угла
AOB» задает то же точечное множество, что и свойство «угол AOM
равен углу M OB» (здесь рассматриваются точки плоскости, лежа- щие внутри угла AOB, см. рис. 1). А в арифметике свойство «целое число делится на 2» задает то же множество, что и свойство «по- следняя цифра целого числа делится на 2».
Иногда бывает трудно доказать равносильность двух характери- стических свойств. Попробуйте, например, доказать, что следующие свойства задают одно и то же множество точек, лежащих в одной плоскости с треугольником ABC:

Как задают множества
9
а) основания перпендикуляров, опущенных из точки M на сто- роны треугольника ABC, лежат на одной прямой;
б) точка M лежит на окружности, описанной вокруг треуголь- ника ABC (рис. 2).
(Совпадение этих множеств составляет содержание так называе- мой теоремы Симсона и теоремы, обратной ей.)
Рис. 1
Рис. 2
Вообще, во многих математических теоремах речь идет о совпаде- нии двух множеств, например множества равносторонних треуголь- ников с множеством равноугольных треугольников, множества опи- санных четырехугольников с множеством четырехугольников, сум- мы противоположных сторон которых равны, и т. д. В некоторых случаях проблема совпадения или различия двух множеств, задан- ных своими характеристическими свойствами, не решена до сих пор.
Так, до сих пор неизвестно, совпадает ли множество {1093, 3511}
с множеством простых чисел n, для которых 2
n
− 2 делится на n
2
Еще большие трудности при задании множеств их характеристи- ческими свойствами возникают из-за недостаточной четкости обы- денного языка, неоднозначности человеческой речи. Большое число промежуточных форм затрудняет разграничение объектов на при- надлежащие и не принадлежащие данному множеству. Пусть, напри- мер, речь идет о множестве всех деревьев на земном шаре. В первую очередь здесь надо определить, идет ли речь обо всех деревьях, кото- рые существовали и будут существовать на Земле, или о деревьях,
существовавших в течение некоторого фиксированного промежут- ка времени (например, с 1 мая по 1 сентября 1965 года). Но тогда возникает вопрос, как быть с деревьями, спиленными за этот проме- жуток времени? Кроме того, существует целый ряд промежуточных форм между деревьями и другими растениями, и надо решить, какие из них относятся к множеству деревьев, а какие нет.
Даже множество планет Солнечной системы определено не впол- не однозначно. Наряду с большими планетами (Меркурием, Венерой,

10
Глава I. Множества и действия над ними
Землей, Марсом, Юпитером, Сатурном, Ураном, Нептуном и Плу- тоном) вокруг Солнца обращается около 1600 малых планет, так называемых астероидов. Поперечники некоторых таких планет (Це- реры, Паллады, Юноны и других) измеряются сотнями километров,
но есть и астероиды, поперечник которых не превышает 1 км. По ме- ре улучшения методов наблюдения астрономы будут открывать все более и более мелкие планеты, и наконец возникнет вопрос, где же кончаются планеты и начинаются метеориты и космическая пыль.
Аналогичное затруднение было у одного героя Бабеля, вопившего после налета банды Бени Крика: «Где начинается полиция и где кон- чается Беня?» Как известно, мудрые одесситы отвечали ему, что по- лиция кончается именно там, где начинается Беня Крик. Но вряд ли фраза «Планеты кончаются именно там, где начинаются метеори- ты» устроит кого-либо в качестве точного определения множества планет Солнечной системы.
Впрочем, разница между планетами и метеоритами интересует в основном астрономов. А вот разница между домом и хибаркой существенна для обитателя любого жилища. Но легко представить себе, что одно и то же здание получит от одного человека уважитель- ное название «дом», а от другого — пренебрежительное прозвище
«хибарка». Разумеется, и отнесение того или иного здания к множе- ству дворцов существенно зависит от того, кому поручено составить список этого множества.
Точно так же рассмотрение множества всех стихотворений, опуб- ликованных в России, осложняется наличием многочисленных про- межуточных форм между стихами и прозой (ритмическая проза,
белые стихи и т. д.). Не слишком точно определено и множество лиц,
пользующихся правом бесплатного проезда по железным дорогам страны. К этому множеству относятся, в частности, дети до 5 лет.
Но может случиться, что малолетнему пассажиру исполнится 5 лет в пути, и тогда неясно, относится ли он к этому множеству (расска- зывают, что один пунктуальный отец включил стоп-кран в момент,
когда его сыну исполнилось пять лет, чтобы точно определить остав- шийся отрезок пути, за который ему следовало уплатить).
Тонкости возникают и в более простых случаях и связаны с неточностью и несовершенством обычного языка. Пусть, на- пример, A есть множество, состоящее из первых n натуральных чисел, A = {1, 2, . . . , n}, где n — число букв первой строки основного текста «Евгения Онегина». Такое определение можно понимать дво- яко. С одной стороны, под числом n можно понимать совокупное

Брить или не брить?
11
количество всех вхождений букв в первую строку (так сказать,
общее количество типографских знаков в строке). Выпишем эту строку и отметим различные вхождения одной и той же буквы соответствующими порядковыми номерами:
М
1
, О
1
, Й
1
,
Д
1
, Я
1
, Д
2
, Я
2
,
С
1
, А
1
, М
2
, Ы
1
, Х
1
,
Ч
1
, Е
1
, С
2
, Т
1
, Н
1
, Ы
2
, Х
2
,
П
1
, Р
1
, А
2
, В
1
, И
1
, Л
1
Получается, что n = 25 и A = {1, 2, . . . , 25}.
С другой стороны, под числом n можно понимать общее число различных букв русского алфавита, встречающихся в первой строке.
Вот эти буквы:
М, О, Й, Д, Я, С, А, Ы, Х, Ч, Е, Т, Н, П, Р, В, И, Л.
Тогда получается, что n = 18 и A = {1, 2, . . . , 18}.
Приведенный пример показывает, с какой тщательностью нужно формулировать определение множества, чтобы избежать неясности и двусмысленности, свойственных обычному нашему языку.

Брить или не брить?
Не всегда затруднения с определением состава множества зави- сят только от недостатков языка. Иногда причина лежит гораздо глубже. Приведем следующий пример. Как правило, сами множе- ства не являются своими собственными элементами (например, мно- жество всех натуральных чисел не является натуральным числом,
множество всех треугольников не является треугольником и т. д.).
Однако бывают и такие множества, которые содержат себя в ка- честве одного из своих элементов. Скажем, множество абстрактных понятий само является абстрактным понятием (не правда ли?). Так как такие множества рассматриваются редко, назовем их экстраор- динарными, а все остальные множества — ординарными.
Образуем теперь множество A, элементами которого являются все ординарные множества. На первый взгляд кажется, что в этом определении нет ничего плохого; не видно, почему фраза «множе- ство всех ординарных множеств» хуже, чем фраза «множество всех треугольников». Но на самом деле здесь возникает серьезное логи- ческое противоречие. Попробуем выяснить, каким же является само полученное множество A — ординарным или экстраординарным. Ес- ли оно ординарно, то оно входит в себя как один из элементов (мы

12
Глава I. Множества и действия над ними ведь собрали вместе все ординарные множества). Но тогда по опре- делению оно является экстраординарным. Если же множество A экс- траординарно, то по определению экстраординарности оно должно быть своим собственным элементом, а среди элементов множества A
есть лишь ординарные множества, экстраординарных множеств мы не брали!
Получилось логическое противоречие — множество A не может быть ни ординарным, ни экстраординарным. Впрочем, такие логи- ческие противоречия возникают и в гораздо более простых случаях.
Например, одному солдату приказали брить тех и только тех сол- дат его взвода, которые не бреются сами. Возник вопрос, как ему поступать с самим собой. Если он будет брить себя, то его следует отнести к числу солдат, которые бреются сами, а брить таких солдат он не имеет права. Если же он себя брить не будет, то его придется отнести к числу солдат, которые сами не бреются, а тогда по приказу он должен себя брить.