Знаки больше и меньше в математике становятся известны детям еще до поступления в первый класс. Часто детки путают, что означает конкретный символ. Родители могут помочь своим чадам в этом вопросе, что положительно повлияет на успеваемость детей. Эти знания пригодятся малышам и в будущем – при изучении геометрии, на уроках алгебры, в примерах, где используется квадратная, а также другая степень чисел. Советы из дан статьи помогут родителям научить малышей важной математической премудрости.
Математические знаки в картинках для дошкольников
Ниже представлено цветное оформление математических символов. При обучении их можно использовать непосредственно с экрана монитора или же их можно распечатать на цветном принтере.
Знак «больше» – в какую сторону
Знак «больше» пишется так «>». Символ обозначается стрелкой, направление острого угла которой обращено в правую сторону. Немного теории: определяющим фактором является левая сторона символа. Если стрелка начинается с двух линий, которые в правой части сходятся в одну точку, тогда это знак «>».
Знак «меньше» – как правильно писать
Знак «меньше» выглядит так «<». Если сказать просто, то стрелка должна смотреть влево. И снова для определения важна левая часть стрелки. Если точка, из которой выходят две линии, расположена слева, то это символ «<».
Знаки «больше или равно» / «меньше или равно»
Знаки «больше или равно» и «меньше или равно» выглядят соответственно так «≥», «≤». Они являются результатом объединения двух символов – «>» или «<» и одной линии.
Эта линия находится под стрелкой. При этом нет пересечения стрелки с линией под ней. Обычно нижняя линия следует принципу параллельности по отношению к нижней части символа.
Данные знаки используются в нестрогих неравенствах. В первом классе такие неравенства обычно не изучают.
Примеры на сравнение чисел для 1 класса
В первом блоке примеров (Таблица 1) нужно поставить правильный символ. Справа и слева стоят только однозначные числа.
Второй блок примеров (Таблица 2) содержит примеры, в которых нужно сопоставить суммы чисел. В случае равенства необходимо вписать знак «равно».
Игры для быстрого запоминания знаков «больше» и «меньше»
Существуют различные логические игры с использованием математических символов. Таких игр множество. Ниже приводятся три игры, где детям нужно поиграться со стрелками «>» и «<».
Игра «Большой голодный крокодил»
Это самый легкий и наглядный способ раз и навсегда запомнить, в какую сторону пишутся знаки «больше» и «меньше». На листе бумаги необходимо нарисовать две круглые тарелки. Диаметр каждой тарелки должен быть не менее 10 сантиметров.
На каждую из «тарелок» можно положить что-то приблизительно напоминающее еду. Например, можно слепить шарики из пластилина или соленого теста и договориться с ребенком, что горошины означают котлеты для крокодила. Для этой игры достаточно смастерить один символ. Его можно сделать на маленькой карточке. Обозначения «>» и «<» примерно напоминают подобие раскрытого рта крокодила.
Важное условие — крокодил выбирает всегда только ту тарелку, на которой больше еды! Об этом нужно сказать ребенку.
На обе «тарелки» необходимо выложить определенное количество «котлет». Затем пусть ребенок положит карточку так, чтобы «рот крокодила» был обращен в сторону «тарелки» на которой больше «котлет».
Игра «Что больше?»
В этой игре комбинация большого и указательного пальцев левой руки имеет значение символа «<», а комбинация большого и указательного пальцев правой руки представляет собой символ «>». Для обозначения того, что больше, достаточно протянуть правую руку, а левая рука нужна для обозначения того, что меньше.
В этой игре для сравнения можно использовать не только числа, но и изображения различных предметов, а также геометрические фигуры разных размеров. Эту игру-занятие можно выполнять во время приема пищи, разложив на столе печенье, конфеты, яблоки и другие продукты. Вот так можно запомнить правильное написание знаков задолго до школы.
Игра «Кубики и доски»
Эта игра принадлежит к разряду активных игр, так как детям нужно совершать действия не только умственного характера, но и быть активными строителями. Для этой игры понадобятся следующие принадлежности: большие кубики и две прямых доски. Одну доску нужно положить на горизонтальную поверхность. На оба края лежащей доски нужно выложить кубики в столбики.
Важно чтобы столбики быть ровными, как восклицательный знак. К примеру, первый (левый) столбик состоит из 4-х кубиков, а второй из 2-х. Затем нужно положить вторую доску на оба столбика. В итоге сочетание нижней и верхней досок покажет правильный символ. В данном примере получится обозначение «>».
С каждым последующим разом можно изменять количество кубиков в столбиках. Когда столбики будут содержать одинаковое количество кубиков – доски покажут «равно».
Заключение
Итак, в математике обозначения «>» и «<» используются довольно часто. Малыши способны освоить принцип их применения довольно рано. Воспользовавшись советами из этой статьи, родители помогут своим детям сделать это быстро и в увлекательной форме.
Математика – царица наук, а арифметика – царица математики. В повседневной жизни нам часто приходится что-либо считать, а потом и оформлять наши подсчёты в письменном виде. В процессы письменного оформления соотношений величин мы нередко используем знаки «Больше» или «Меньше». При этом многие люди, непосредственно не занятые арифметикой на бумаге, могут со временем позабыть, в какую из сторон (левую или правую) пишутся данные знаки. В нашем материале мы подробно разберём, в какую из сторон пишется знак больше, меньше или равно, и какие приёмы позволят эффектно запомнить изложенную информацию.
- Как пишется знак больше меньше в математике
- Что значит «меньше или равно»?
- Обучение с использованием символов «больше» или «меньше»
- Объединение знаков
- Ключевые советы по работе с неравенствами
- Знаки больше или меньше на клавиатуре
- Видео:
Как пишется знак больше меньше в математике
Знаки «больше (>)» или «меньше (<)» обычно используются для отображения отношений между числами. Они позволяют продемонстрировать, какое число имеет большее или меньшее значение, и применяются с целью помочь учащимся разобраться с соотношениями чисел. Знаки «больше» или «меньше» также часто известны как знаки «больше чем» и «меньше чем».
Широкий конец данного знака всегда обращён к большему числу. Например:
25 > 10
100 > 50
500 > 200
Знак «больше» (>) означает, что число перед знаком «больше» всегда больше числа, которое находится после данного знака.
200 > 100
Знак меньше (<) означает, что число перед данным знаком всегда меньше, нежели число после данного знака. Как видим, визуально знак «больше» и «меньше» — это просто перевернутые версии одного и того же символа.
100 < 200
Знак равенства (=) означает, что число после знака равно числу перед знаком.
Важно! Знак равенства не является показателем результата работы над числами (например, 3+5=8). Данный знак показывает, что сумма чисел слева равна сумме чисел справа. То есть 3+5 слева равно числу справа, которым и является 8.
Когда же два значения определенно не равны, тогда мы используем пример со знаком «не равно»: 2+2 ≠ 9. То есть сумма значений чисел слева (4) не равно значению чисел справа (9).
Читайте также: как посчитать разницу в процентах между двумя имеющимися числами.
Что значит «меньше или равно»?
Разобрав, в какую именно сторону пишутся знаки больше, меньше или равно, разберём также ситуации, когда какое-либо значение меньше, но может быть также равно. Например, чайник может вмещать до 10 стаканов воды. Так сколько в нём может быть воды? Это может быть 10 стаканов или меньше 10 стаканов. Пока мы не измерим количество жидкости, то всё, что мы можем сказать о наполнении стакана, то это то, что оно «меньше или равно» 10 стаканам.
Для показа данного отношения с помощью символов мы добавляем внизу дополнительную строку символа больше или меньше. Например:
- Знак «больше или равно»: ≥
- Знак «меньше или равно»: ≤
Зачем использовать данные знаки? Дело в том, что есть вещи, полной информации о которых мы не имеем, но, тем не менее, можем о них что-то полагать. Таким образом, у нас есть различные способы сказать то, что мы знаем, хоть и не до конца (это может быть полезно).
Пример:
У Олега было 10 яблок, но он потерял несколько. Сколько у него сейчас?
Ответ: У него должно быть меньше 10 яблок.
То есть: яблоки у Олега < 10
Если у Олега все еще есть яблоки, мы также можем сказать, что у него больше нуля яблок? Конечно.
То есть: яблоки у Олега > 0
Но если бы мы думали, что Олег мог потерять все свои яблоки, мы бы сказали:
яблоки у Олега ≥ 0
Другими словами, количество яблок больше или равно нулю.
Это пригодится: решение примеров по фотографии онлайн.
Обучение с использованием символов «больше» или «меньше»
Дети знакомятся с символами «больше» и «меньше» ещё в 1 классе, в процессе обучения пониманию единиц, из которых могут быть составлены числа. Но они не всегда могут запомнить правильную позицию данного знака. В этом случае им могут помочь пару полезных способов.
Способ №1. Рот крокодила
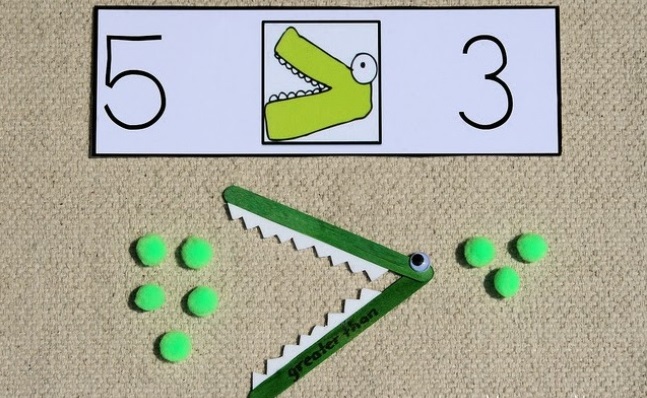
Самый распространенный способ объяснить, как работают символы «больше чем» и «меньше чем», — это сравнить их со пастью крокодила. Нужно объяснить, что крокодил всегда хочет наесться побольше, и съесть большее число. Это простое и красочное объяснение, апеллирует к воображению детей и помогает им правильно использовать данные символы.
Например, если у нас есть числа 72 и 45, мы могли бы сказать, что крокодил хочет съесть число 72, так как это число с более высоким значением. Затем мы добавим символы, чтобы это выглядело так:
72 > 45 (пасть крокодила направлена в сторону большего числа).
Способ №2. Метод точек
Знаки больше или меньше можно сравнить с тремя точка. Там где меньшая сторона знака – там одна точка посередине, а где большая – две точки, одна снизу, а вторая сверху. Выглядит это примерно так:
Мы ставим две точки всегда к числу, которое больше другого. И одной точкой – к числу, которое меньше другого. Таким образом, вы всегда поставите нужный символ.
Объединение знаков
Иногда мы можем объединить два (или более) сочетания в одной строке:
Пример: Аня имеет 100 рублей, покупает что-то и говорит: «У меня есть сдача».
Сколько же она могла потратить?
Ответ: что-то больше 0 рублей и меньше 100 рублей (но НЕ 0 или 100 рублей):
«Сколько Аня тратит» > 0 рублей
«Что тратит Аня» < 100 рублей
Это можно записать всего в одну строку:
Рублей 0 < «Сколько Аня тратит» < Рублей 100.
Ключевые советы по работе с неравенствами
Выяснив, в какую сторону пишутся символы больше, меньше или равно, упомянем также работу с неравенствами. Неравенства сложны, так мы привыкли иметь четкие ответы на математические задачи, но неравенства не всегда дают нам это. Когда вы имеете с неравенством, помните о следующих правилах для облегчения процесса:
- Изолируйте переменные. При работе в неравенствах с переменными, важно помнить, что вы пытаетесь изолировать переменную в ту или иную сторону. Сосредоточьтесь на сжатии чисел, если это возможно, с целью получить одну переменную в обеих сторонах вашего уравнения;
- Отрицательные числа изменяют знак больше или меньше. Не забывайте, что выполнение определенных действий может переворачивать знак. Когда вы умножаете или делите на отрицательное число, будет необходимо перевернуть знак «меньше» или «больше» вместе с ним;
- Избегайте умножения или деления на переменные. Если вы не уверены, что переменная всегда будет положительной или отрицательной, не умножайте и не делите неравенство на указанную переменную.
Знаки больше или меньше на клавиатуре
Знаки «больше» или «меньше» можно найти на клавиатуре внизу справа, переключившись на английскую раскладку. Достаточно зажать клавишу «Shift», и нажав на кнопку «Б» вы получите знак «меньше» (<), а нажав на кнопку «Ю» — знак «больше» (>).
Видео:
В нашем материале мы разобрали, в какую сторону направлен символ больше, меньше или равно, как не ошибиться с употреблением данных знаков, и что при этом стоит учитывать. Используйте представленный нами инструментарий, позволяющий разобраться в правильном применении данных знаков. И избежать ошибок при письменном оформлении соотношений имеющихся у вас чисел.
Содержание материала
- Как и в какую сторону пишется знак больше
- Равенство и неравенство
- Знаки «больше или равно» / «меньше или равно»
- Знак «меньше» – как правильно писать
- Графический способ
- «Стрелочки»
- Игры для быстрого запоминания знаков «больше» и «меньше»
- Игра «Большой голодный крокодил»
- Игра «Что больше?»
- Игра «Кубики и доски»
- Сортировка
- Популярное
- Найди закономерность
- Как решать ребусы?
Как и в какую сторону пишется знак больше
В общем и целом логика понимания очень проста — какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону — такой и знак. Соответственно, знак больше влево смотрит широкой стороной — большей.
Пример использования знака больше:
- 50>10 — число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.
Равенство и неравенство
Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.
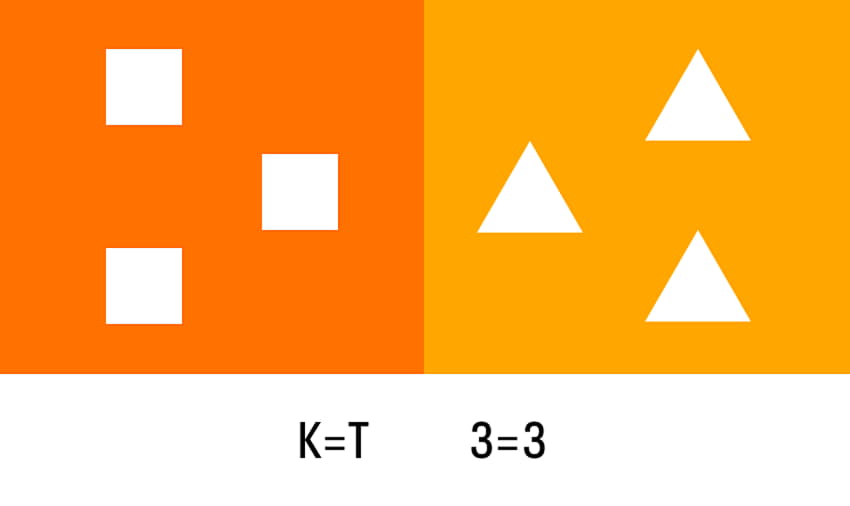
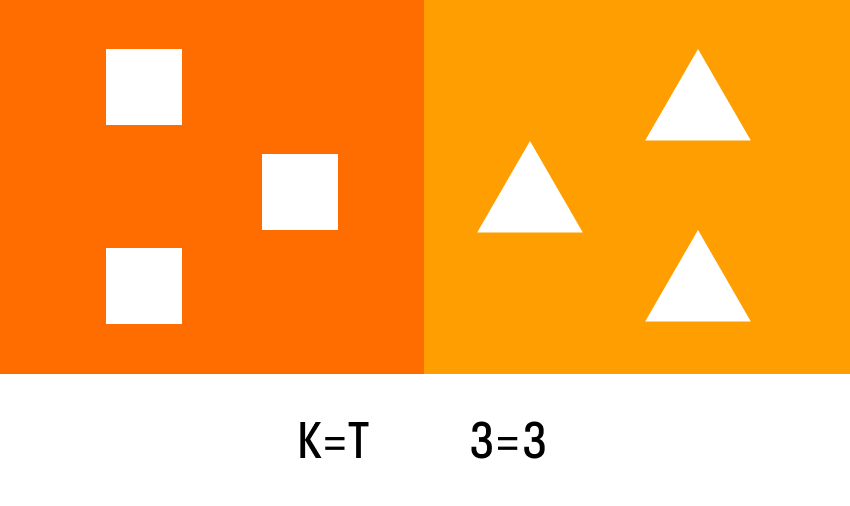
Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».
Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
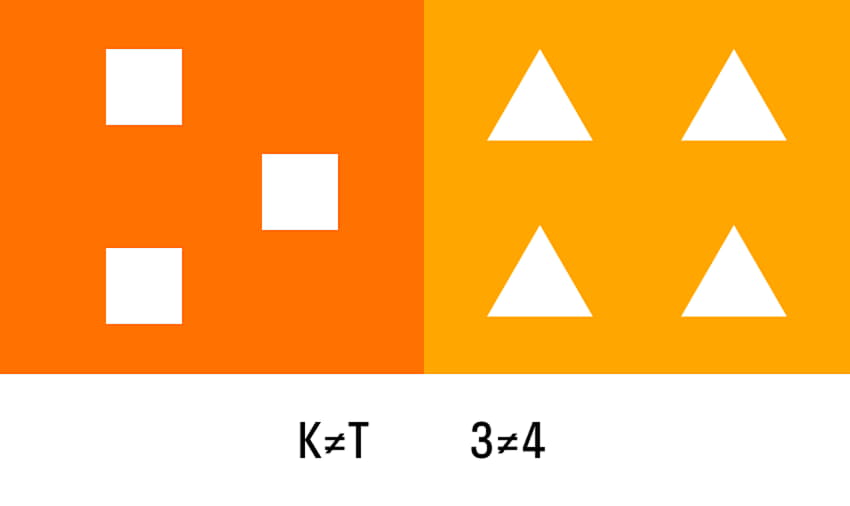
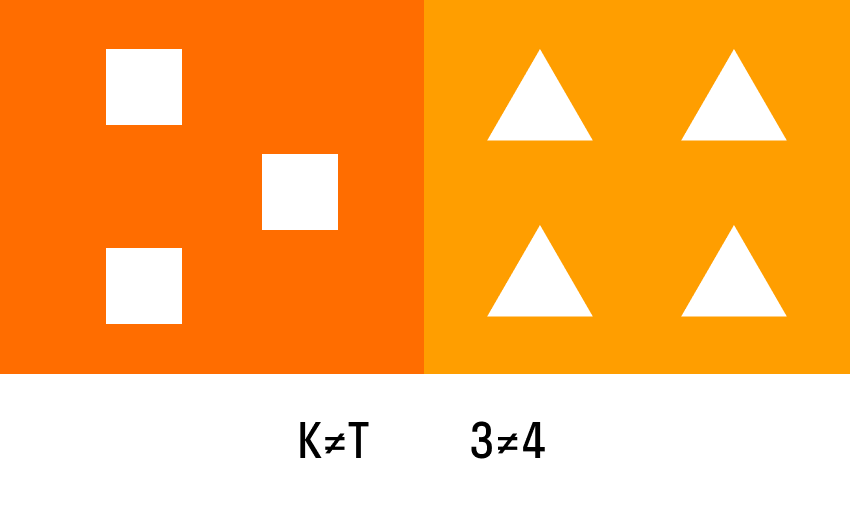
Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.
Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:
Знаки «больше или равно» / «меньше или равно»
Знаки «больше или равно» и «меньше или равно» выглядят соответственно так «≥», «≤». Они являются результатом объединения двух символов – «>» или «<» и одной линии.

Эта линия находится под стрелкой. При этом нет пересечения стрелки с линией под ней. Обычно нижняя линия следует принципу параллельности по отношению к нижней части символа.
Данные знаки используются в нестрогих неравенствах. В первом классе такие неравенства обычно не изучают.
Знак «меньше» – как правильно писать
Знак «меньше» выглядит так «<». Если сказать просто, то стрелка должна смотреть влево. И снова для определения важна левая часть стрелки. Если точка, из которой выходят две линии, расположена слева, то это символ «<».
Графический способ
Данный метод подойдет тем, кто уже прошел обучение одним из вышеперечисленных способов и хорошо ориентируется. Не рекомендуется начинать с него изучение ребенку дошкольного возраста.
Суть заключается в том, что нужно на листе бумаги нарисовать знаки «>» и «<» достаточно большого размера. В первом случае если смотреть слева, то расстояние между линиями достаточно большое — значит, это и есть символ «больше». У второго знака расстояние с левой стороны маленькое, соответственно это и есть «меньше».
«Стрелочки»
Детям младших классов нужно объяснять знаки на принципе сопоставления их стрелкам, которые направлены в противоположные стороны. В этом случае важно уточнить, что стрелка всегда показывает на то число, которое меньше. Если ребенок это усвоит, то трудностей с постановкой знаков у него не будет. Он с легкостью определит, как правильно поставить стрелку.
Трудности возникают у детей во время чтения выражений. Но и их легко устранить: если знак будет поставлен правильно, то и выражение они прочтут без проблем. После выполнения небольшого количества заданий ребенку станет ясно, что стрелка, направленная в левую сторону, означает знак «меньше», если в правую – «больше».
Игры для быстрого запоминания знаков «больше» и «меньше»
Существуют различные логические игры с использованием математических символов. Таких игр множество. Ниже приводятся три игры, где детям нужно поиграться со стрелками «>» и «<».
Игра «Большой голодный крокодил»
Это самый легкий и наглядный способ раз и навсегда запомнить, в какую сторону пишутся знаки «больше» и «меньше». На листе бумаги необходимо нарисовать две круглые тарелки. Диаметр каждой тарелки должен быть не менее 10 сантиметров.
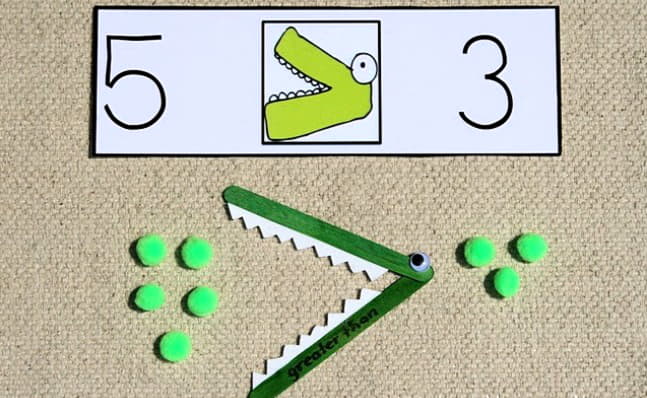
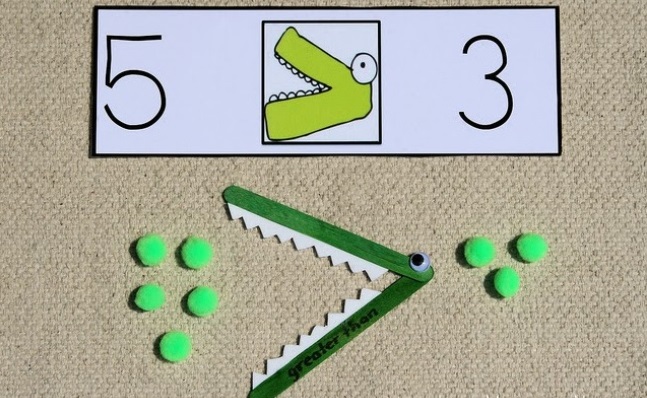
На каждую из «тарелок» можно положить что-то приблизительно напоминающее еду. Например, можно слепить шарики из пластилина или соленого теста и договориться с ребенком, что горошины означают котлеты для крокодила. Для этой игры достаточно смастерить один символ. Его можно сделать на маленькой карточке. Обозначения «>» и «<» примерно напоминают подобие раскрытого рта крокодила.
Важное условие — крокодил выбирает всегда только ту тарелку, на которой больше еды! Об этом нужно сказать ребенку.
На обе «тарелки» необходимо выложить определенное количество «котлет». Затем пусть ребенок положит карточку так, чтобы «рот крокодила» был обращен в сторону «тарелки» на которой больше «котлет».
Игра «Что больше?»
В этой игре комбинация большого и указательного пальцев левой руки имеет значение символа «<», а комбинация большого и указательного пальцев правой руки представляет собой символ «>». Для обозначения того, что больше, достаточно протянуть правую руку, а левая рука нужна для обозначения того, что меньше.
В этой игре для сравнения можно использовать не только числа, но и изображения различных предметов, а также геометрические фигуры разных размеров. Эту игру-занятие можно выполнять во время приема пищи, разложив на столе печенье, конфеты, яблоки и другие продукты. Вот так можно запомнить правильное написание знаков задолго до школы.
Игра «Кубики и доски»
Эта игра принадлежит к разряду активных игр, так как детям нужно совершать действия не только умственного характера, но и быть активными строителями. Для этой игры понадобятся следующие принадлежности: большие кубики и две прямых доски. Одну доску нужно положить на горизонтальную поверхность. На оба края лежащей доски нужно выложить кубики в столбики.

Важно чтобы столбики быть ровными, как восклицательный знак. К примеру, первый (левый) столбик состоит из 4-х кубиков, а второй из 2-х. Затем нужно положить вторую доску на оба столбика. В итоге сочетание нижней и верхней досок покажет правильный символ. В данном примере получится обозначение «>».
С каждым последующим разом можно изменять количество кубиков в столбиках. Когда столбики будут содержать одинаковое количество кубиков – доски покажут «равно».
Сортировка
Остается одно понятие, неразрывно связанное с понятием сравнения, речь идет о сортировке.
Ряд различных чисел будем называть отсортированным по возрастанию, если каждое следующее число в нем больше предыдущего.
Пример ряда, отсортированного по возрастанию:
1, 4, 6, 32, 99, 100, 127
Посмотрим на другой ряд:
1, 6, 2, 9, 12
Его уже нельзя назвать отсортированным по возрастанию, так как третий элемент меньше второго.
Но если мы поменяем их местами, то ряд
1, 2, 6, 9, 12
уже отсортирован по возрастанию.
Также сортировка может быть по убыванию.
Ряд различных чисел будем называть отсортированным по убыванию, если каждое следующее число в нем меньше предыдущего.
Например, такой ряд можно назвать отсортированным по убыванию:
436, 387, 124, 76, 9, 2
А вот про такой ряд этого уже нельзя будет сказать:
363, 236, 481, 13, 5
Данный ряд не является отсортированным по убыванию, так как третий элемент больше второго.
Сортировка — довольно распространенное понятие.
В практически любом интернет-магазине можно увидеть выбор сортировки. Если речь идет про цену, то это как раз будет сортировка по убыванию или по возрастанию.
В информатике и компьютерных науках алгоритмы сортировки являются базовыми, о них вы узнаете позже в соответствующих курсах.
Пока важно запомнить сами определению.
Пройти тест Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации Вход Регистрация
Популярное

Навыки 15 декабря 2019

Математика 26 августа 2019 Найди закономерность Закономерность — это регулярные устойчивые взаимосвязи в количествах, свойствах и явлениях объектов. В математической закономерности нужно найти алгоритм, согласно которому в цепочке чисел происходит их повторение, изменение или замещение в соответствии с установленным правилом.

Любовь к учебе 6 сентября 2019 Как решать ребусы? Разгадывание ребусов – отличное времяпровождение для любителей всевозможных головоломок и загадок. Это захватывающий процесс, суть которого заключается в том, чтобы расшифровать слово, фразу или предложение с помощью картинок и символов-подсказок: цифр, букв, запятых и прочих знаков.
Теги
Математические знаки
Скорее всего, к первому классу ребенок уже отличает на слух и визуально, что горстка из десяти ягод больше трех штук. Чтобы внедрить в жизнь новые обозначения, посмотрим на знаки «больше», «меньше», «равно» в картинках.
Символ больше (>) — это когда острый нос галочки смотрит направо. Его нужно использовать, когда первое число больше второго:
Символ меньше (<) — это когда острый нос галочки смотрит налево. Его нужно использовать, когда первое число меньше второго:
Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:
Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:
Ниже представлено цветное оформление математических символов. При обучении их можно использовать непосредственно с экрана монитора или же их можно распечатать на цветном принтере.
Как и в какую сторону пишется знак больше
Знак «больше» пишется так «>». Символ обозначается стрелкой, направление острого угла которой обращено в правую сторону. Немного теории: определяющим фактором является левая сторона символа. Если стрелка начинается с двух линий, которые в правой части сходятся в одну точку, тогда это знак «>».
В общем и целом логика понимания очень проста — какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону — такой и знак. Соответственно, знак больше влево смотрит широкой стороной — большей.
Пример использования знака больше:
- 50>10 — число 50 больше числа 10;
- посещаемость студента в этом семестре составила >90% занятий.
Как и в какую сторону пишется знак меньше
Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной — меньшей, то перед вами знак меньше.
Пример использования знака меньше:
100 =», что, в принципе, часто вполне допустимо, но можно сделать красивее и правильнее.
На самом деле для того, чтобы напечатать эти знаки, существуют специальные символы, которые можно ввести на любой клавиатуре. Согласитесь, знаки «≤» и «≥» выглядят значительно лучше.
Знак «меньше» выглядит так «<». Если сказать просто, то стрелка должна смотреть влево. И снова для определения важна левая часть стрелки. Если точка, из которой выходят две линии, расположена слева, то это символ «<».
- 100<500 — число 100 меньше числа пятьсот;
- на заседание явилось <50% депутатов.
Как видите, все довольно логично и просто, так что теперь вопросов о том, в какую сторону писать знак больше и знак меньше в будущем у вас возникать не должно.
Знаки больше и меньше на клавиатуре
Символы больше (>) и меньше (<) находятся на всех компьютерных клавиатурах, на тех же клавишах что и буквы «Б» и «Ю» в русской раскладке клавиатуры. Чтобы использовать знак больше или меньше нужно переключиться на английский язык и удерживая Shift нажать по нужному символу. Знаки больше и меньше напоминают стрелки, указывающие вправо и влево, они широко используются в математике и программировании.
Ниже приведен пример того, как могут быть использованы эти знаки в математике. Пример показывает, что число 10 больше 2 и число 5 меньше 8.
10>2
5<8
Следующий пример показывает как знак больше (или меньше) может быть использован в программировании. В этом примере, если переменная $value больше 100, то на экран выведется предложение «Переменная больше 100», иначе ничего не произойдет.
Знаки «больше или равно» / «меньше или равно»
Знаки «больше или равно» и «меньше или равно» выглядят соответственно так «≥», «≤». Они являются результатом объединения двух символов – «>» или «<» и одной линии.
Эта линия находится под стрелкой. При этом нет пересечения стрелки с линией под ней. Обычно нижняя линия следует принципу параллельности по отношению к нижней части символа.
Данные знаки используются в нестрогих неравенствах. В первом классе такие неравенства обычно не изучают.
Игры для быстрого запоминания знаков «больше» и «меньше»
Существуют различные логические игры с использованием математических символов. Таких игр множество. Ниже приводятся три игры, где детям нужно поиграться со стрелками «>» и «<».
Игра «Большой голодный крокодил»
Это самый легкий и наглядный способ раз и навсегда запомнить, в какую сторону пишутся знаки «больше» и «меньше». На листе бумаги необходимо нарисовать две круглые тарелки. Диаметр каждой тарелки должен быть не менее 10 сантиметров.
На каждую из «тарелок» можно положить что-то приблизительно напоминающее еду. Например, можно слепить шарики из пластилина или соленого теста и договориться с ребенком, что горошины означают котлеты для крокодила. Для этой игры достаточно смастерить один символ. Его можно сделать на маленькой карточке. Обозначения «>» и «<» примерно напоминают подобие раскрытого рта крокодила.
Важное условие — крокодил выбирает всегда только ту тарелку, на которой больше еды! Об этом нужно сказать ребенку.
На обе «тарелки» необходимо выложить определенное количество «котлет». Затем пусть ребенок положит карточку так, чтобы «рот крокодила» был обращен в сторону «тарелки» на которой больше «котлет».
Игра «Что больше?»
В этой игре комбинация большого и указательного пальцев левой руки имеет значение символа «<», а комбинация большого и указательного пальцев правой руки представляет собой символ «>». Для обозначения того, что больше, достаточно протянуть правую руку, а левая рука нужна для обозначения того, что меньше.
В этой игре для сравнения можно использовать не только числа, но и изображения различных предметов, а также геометрические фигуры разных размеров. Эту игру-занятие можно выполнять во время приема пищи, разложив на столе печенье, конфеты, яблоки и другие продукты. Вот так можно запомнить правильное написание знаков задолго до школы.
Игра «Кубики и доски»
Эта игра принадлежит к разряду активных игр, так как детям нужно совершать действия не только умственного характера, но и быть активными строителями. Для этой игры понадобятся следующие принадлежности: большие кубики и две прямых доски. Одну доску нужно положить на горизонтальную поверхность. На оба края лежащей доски нужно выложить кубики в столбики.
Важно чтобы столбики быть ровными, как восклицательный знак. К примеру, первый (левый) столбик состоит из 4-х кубиков, а второй из 2-х. Затем нужно положить вторую доску на оба столбика. В итоге сочетание нижней и верхней досок покажет правильный символ. В данном примере получится обозначение «>».
С каждым последующим разом можно изменять количество кубиков в столбиках. Когда столбики будут содержать одинаковое количество кубиков – доски покажут «равно».
Равенство и неравенство
Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.
Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».
Неравенство — алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.
Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.
Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:
Типы неравенств
- Строгие неравенства — используют только знак больше (>) или меньше (<).
- a < b — это значит, что a меньше, чем b.
- a > b — это значит, что a больше, чем b.
- неравенства a > b и b < a означают одно и то же, то есть равносильны.
- Нестрогие неравенства — используют знаки сравнения ≥ (больше или равно) или ≤ (меньше или равно).
- a ≤ b — это значит, что a меньше либо равно b.
- a ≥ b — это значит, что a больше либо равно b.
- знаки ⩽ и ⩾ являются противоположными.
- Другие типы неравенств.
- a ≠ b — означает, что a не равно b.
- a ≫ b — означает, что a намного больше, чем b.
- a ≪ b — означает, что a намного меньше, чем b.
- знаки >> и << противоположны.
Источники
- https://skysmart.ru/articles/mathematic/znaki-bolshe-menshe-ili-ravno
- https://kakpravilno05.ru/kak-pishetsja-znaki-bolshe-i-menshe-v-matematike/
- https://linchakin.com/%D1%81%D0%BB%D0%BE%D0%B2%D0%B0%D1%80%D1%8C/%D0%B7/%D0%B7%D0%BD%D0%B0%D0%BA%D0%B8_%D0%B1%D0%BE%D0%BB%D1%8C%D1%88%D0%B5_%D0%B8_%D0%BC%D0%B5%D0%BD%D1%8C%D1%88%D0%B5/
- https://nauka.club/matematika/znak-bolshe-i-menshe.html
- https://Sprint-Olympic.ru/uroki/matematika-uroki/92800-znaki-bolshe-i-menshe-v-matematike-sravnenie-chisel-s-primerami.html
[свернуть]
Доброго времени суток, уважаемые родители и маленькие школьники! Сегодня спешу поделиться с вами своим открытием. Недавно нашла в интернете, уже не помню точно где, решение проблемы, которая частенько подстерегает дошколят и учеников 1-х классов, которые только начинают свое знакомство с математикой.
Статья адресована всем тем, кого одолевает вопрос: «Знаки больше меньше в какую сторону пишутся?» Больше это как? Уголочком налево? Или направо? А может быть, это не больше, а меньше? Вспомните, родители, у вас в школе были проблемы с этими коварными значками? И как вам объяснял эту тему учитель?
Если честно, я не помню, как объясняли мне, но точно не так, как я вам собираюсь показать. Все гениальное просто!
Давайте для начала посмотрим на исследуемые в статье знаки. Это «больше». Вот он, в примере на картинке.
Он ставится, когда первое число в неравенстве больше второго. Острие галочки направлено вправо.
А это его товарищ – «меньше».
Ставим его тогда, когда первое число неравенства (то, что левее) меньше, чем второе. Уголочек галочки направлен влево.
Вроде, все понятно, но в светлых головах наших маленьких школьников возникает путаница. Давайте на пример посмотрим. Вот какой знак сюда нужно поставить?
Дети наши — не глупые ребята. Они прекрасно знают, что тройка меньше шестерки. И значит, знак нужно ставить «меньше». Вот только, как он выглядит? Уголочек куда направлен: влево, вправо? Вот в этом месте и случается основной ступор. Ну как же запомнить-то?
И вот мы переходим к главному секрету! Нам поможет метод точек!!! Только посмотрите, как все просто. Внимание на картинку.
У нас два числа, которые необходимо сравнить. Мы понимаем, что, к примеру, число 8 меньше, чем 9. Около меньшего числа (восьмерочки) ставим одну точечку, так, как на картинке, а около большего (девяточки) — две. А потом просто соединяем эти точки, получаем нужный знак! И дело в шляпе!
Еще раз попробуем.
Согласитесь, очень просто! И понятно! И намного легче, нежели рассказы про раскрытые клювики голодных птичек или острие стрелы направленное на меньшее число.
Надеюсь, вам пригодится этот способ запоминания, и детишки никогда не будут снова ошибаться!
Чем больше ребенок будет тренироваться, чем больше чисел он сравнит, тем быстрее он доведет навык выбора нужного значка до автоматизма. Устраивать такие «сравнительные» тренировки можно в обычной тетрадке или в специальном учебном пособии, которых навалом в магазинах.
Но! Есть способ и поинтереснее)
Мы тут кое-что изобрели, хотим похвастаться.
Та-дам! Представляем вам наш волшебный инструмент для запоминания угловатых значков!
Встречайте! Его Величество — Абак!
Абак — это тренажер, который помогает отработать тему.
Чтобы понять, как им пользоваться, посмотрите это коротенькое объясняющее видео.
Согласитесь, так тренироваться гораздо веселее, чем в обычной тетрадке.
Хотите такой же? Тогда пройдите в наш магазинчик, там все очень подробно.
Хорошая новость! В период с 30 декабря 2021 года по 9 января 2022 года в нашем магазинчике действуют Новогодние скидки! Не пропустите!
А может вам известны другие интересные методы запоминания? Делитесь ими в комментариях)
Кстати, мы уже говорили о том, как запоминать падежи.
Научились умножать на 9 с помощью пальчиков.
И узнали высокоскоростной способ деления на 5.
Посмотрите, это очень интересно! И наверняка пригодится в учебе.
Пожалуйста, не забудьте подписаться на новости блога, чтобы всегда быть в курсе наших событий. И вступайте в нашу группу «ВКонтакте», будем вам очень рады!
Успехов вам!
Ваша «ШколаЛа»
This article is about relations «greater than» and «less than». For the relation «not equal», see Inequation.
In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions.[1] It is used most often to compare two numbers on the number line by their size. There are several different notations used to represent different kinds of inequalities:
- The notation a < b means that a is less than b.
- The notation a > b means that a is greater than b.
In either case, a is not equal to b. These relations are known as strict inequalities,[1] meaning that a is strictly less than or strictly greater than b. Equivalence is excluded.
In contrast to strict inequalities, there are two types of inequality relations that are not strict:
- The notation a ≤ b or a ⩽ b means that a is less than or equal to b (or, equivalently, at most b, or not greater than b).
- The notation a ≥ b or a ⩾ b means that a is greater than or equal to b (or, equivalently, at least b, or not less than b).
The relation not greater than can also be represented by a ≯ b, the symbol for «greater than» bisected by a slash, «not». The same is true for not less than and a ≮ b.
The notation a ≠ b means that a is not equal to b; this inequation sometimes is considered a form of strict inequality.[2] It does not say that one is greater than the other; it does not even require a and b to be member of an ordered set.
In engineering sciences, less formal use of the notation is to state that one quantity is «much greater» than another,[3] normally by several orders of magnitude.
- The notation a ≪ b means that a is much less than b.[4]
- The notation a ≫ b means that a is much greater than b.[5]
This implies that the lesser value can be neglected with little effect on the accuracy of an approximation (such as the case of ultrarelativistic limit in physics).
In all of the cases above, any two symbols mirroring each other are symmetrical; a < b and b > a are equivalent, etc.
Properties on the number line[edit]
Inequalities are governed by the following properties. All of these properties also hold if all of the non-strict inequalities (≤ and ≥) are replaced by their corresponding strict inequalities (< and >) and — in the case of applying a function — monotonic functions are limited to strictly monotonic functions.
Converse[edit]
The relations ≤ and ≥ are each other’s converse, meaning that for any real numbers a and b:
a ≤ b and b ≥ a are equivalent.
Transitivity[edit]
The transitive property of inequality states that for any real numbers a, b, c:[6]
If a ≤ b and b ≤ c, then a ≤ c.
If either of the premises is a strict inequality, then the conclusion is a strict inequality:
If a ≤ b and b < c, then a < c.
If a < b and b ≤ c, then a < c.
Addition and subtraction[edit]
If x < y, then x + a < y + a.
A common constant c may be added to or subtracted from both sides of an inequality.[2] So, for any real numbers a, b, c:
If a ≤ b, then a + c ≤ b + c and a − c ≤ b − c.
In other words, the inequality relation is preserved under addition (or subtraction) and the real numbers are an ordered group under addition.
Multiplication and division[edit]
If x < y and a > 0, then ax < ay.
If x < y and a < 0, then ax > ay.
The properties that deal with multiplication and division state that for any real numbers, a, b and non-zero c:
If a ≤ b and c > 0, then ac ≤ bc and a/c ≤ b/c.
If a ≤ b and c < 0, then ac ≥ bc and a/c ≥ b/c.
In other words, the inequality relation is preserved under multiplication and division with positive constant, but is reversed when a negative constant is involved. More generally, this applies for an ordered field. For more information, see § Ordered fields.
Additive inverse[edit]
The property for the additive inverse states that for any real numbers a and b:
If a ≤ b, then −a ≥ −b.
Multiplicative inverse[edit]
If both numbers are positive, then the inequality relation between the multiplicative inverses is opposite of that between the original numbers. More specifically, for any non-zero real numbers a and b that are both positive (or both negative):
If a ≤ b, then 1/a ≥
1/b.
All of the cases for the signs of a and b can also be written in chained notation, as follows:
If 0 < a ≤ b, then
1/a ≥
1/b > 0.
If a ≤ b < 0, then 0 >
1/a ≥
1/b.
If a < 0 < b, then
1/a < 0 <
1/b.
Applying a function to both sides[edit]
Any monotonically increasing function, by its definition,[7] may be applied to both sides of an inequality without breaking the inequality relation (provided that both expressions are in the domain of that function). However, applying a monotonically decreasing function to both sides of an inequality means the inequality relation would be reversed. The rules for the additive inverse, and the multiplicative inverse for positive numbers, are both examples of applying a monotonically decreasing function.
If the inequality is strict (a < b, a > b) and the function is strictly monotonic, then the inequality remains strict. If only one of these conditions is strict, then the resultant inequality is non-strict. In fact, the rules for additive and multiplicative inverses are both examples of applying a strictly monotonically decreasing function.
A few examples of this rule are:
- Raising both sides of an inequality to a power n > 0 (equiv., −n < 0), when a and b are positive real numbers:
0 ≤ a ≤ b ⇔ 0 ≤ an ≤ bn.
0 ≤ a ≤ b ⇔ a−n ≥ b−n ≥ 0.
- Taking the natural logarithm on both sides of an inequality, when a and b are positive real numbers:
0 < a ≤ b ⇔ ln(a) ≤ ln(b).
0 < a < b ⇔ ln(a) < ln(b).
(this is true because the natural logarithm is a strictly increasing function.)
Formal definitions and generalizations[edit]
A (non-strict) partial order is a binary relation ≤ over a set P which is reflexive, antisymmetric, and transitive.[8] That is, for all a, b, and c in P, it must satisfy the three following clauses:
- a ≤ a (reflexivity)
- if a ≤ b and b ≤ a, then a = b (antisymmetry)
- if a ≤ b and b ≤ c, then a ≤ c (transitivity)
A set with a partial order is called a partially ordered set.[9] Those are the very basic axioms that every kind of order has to satisfy. Other axioms that exist for other definitions of orders on a set P include:
- For every a and b in P, a ≤ b or b ≤ a (total order).
- For all a and b in P for which a < b, there is a c in P such that a < c < b (dense order).
- Every non-empty subset of P with an upper bound has a least upper bound (supremum) in P (least-upper-bound property).
Ordered fields[edit]
If (F, +, ×) is a field and ≤ is a total order on F, then (F, +, ×, ≤) is called an ordered field if and only if:
- a ≤ b implies a + c ≤ b + c;
- 0 ≤ a and 0 ≤ b implies 0 ≤ a × b.
Both (Q, +, ×, ≤) and (R, +, ×, ≤) are ordered fields, but ≤ cannot be defined in order to make (C, +, ×, ≤) an ordered field,[10] because −1 is the square of i and would therefore be positive.
Besides from being an ordered field, R also has the Least-upper-bound property. In fact, R can be defined as the only ordered field with that quality.[11]
Chained notation[edit]
The notation a < b < c stands for «a < b and b < c«, from which, by the transitivity property above, it also follows that a < c. By the above laws, one can add or subtract the same number to all three terms, or multiply or divide all three terms by same nonzero number and reverse all inequalities if that number is negative. Hence, for example, a < b + e < c is equivalent to a − e < b < c − e.
This notation can be generalized to any number of terms: for instance, a1 ≤ a2 ≤ … ≤ an means that ai ≤ ai+1 for i = 1, 2, …, n − 1. By transitivity, this condition is equivalent to ai ≤ aj for any 1 ≤ i ≤ j ≤ n.
When solving inequalities using chained notation, it is possible and sometimes necessary to evaluate the terms independently. For instance, to solve the inequality 4x < 2x + 1 ≤ 3x + 2, it is not possible to isolate x in any one part of the inequality through addition or subtraction. Instead, the inequalities must be solved independently, yielding x < 1/2 and x ≥ −1 respectively, which can be combined into the final solution −1 ≤ x < 1/2.
Occasionally, chained notation is used with inequalities in different directions, in which case the meaning is the logical conjunction of the inequalities between adjacent terms. For example, the defining condition of a zigzag poset is written as a1 < a2 > a3 < a4 > a5 < a6 > … . Mixed chained notation is used more often with compatible relations, like <, =, ≤. For instance, a < b = c ≤ d means that a < b, b = c, and c ≤ d. This notation exists in a few programming languages such as Python. In contrast, in programming languages that provide an ordering on the type of comparison results, such as C, even homogeneous chains may have a completely different meaning.[12]
Sharp inequalities[edit]
An inequality is said to be sharp if it cannot be relaxed and still be valid in general. Formally, a universally quantified inequality φ is called sharp if, for every valid universally quantified inequality ψ, if ψ ⇒ φ holds, then ψ ⇔ φ also holds. For instance, the inequality ∀a ∈ R. a2 ≥ 0 is sharp, whereas the inequality ∀a ∈ R. a2 ≥ −1 is not sharp.[citation needed]
Inequalities between means[edit]
There are many inequalities between means. For example, for any positive numbers a1, a2, …, an we have H ≤ G ≤ A ≤ Q, where they represent the following means of the sequence:
- Harmonic mean
- Geometric mean
- Arithmetic mean
- quadratic mean
Cauchy–Schwarz inequality[edit]
The Cauchy–Schwarz inequality states that for all vectors u and v of an inner product space it is true that
where 
Power inequalities[edit]
A «power inequality» is an inequality containing terms of the form ab, where a and b are real positive numbers or variable expressions. They often appear in mathematical olympiads exercises.
Examples[edit]
- For any real x,
- If x > 0 and p > 0, then
In the limit of p → 0, the upper and lower bounds converge to ln(x).
- If x > 0, then
- If x > 0, then
- If x, y, z > 0, then
- For any real distinct numbers a and b,
- If x, y > 0 and 0 < p < 1, then
- If x, y, z > 0, then
- If a, b > 0, then[13]
- If a, b > 0, then[14]
- If a, b, c > 0, then
- If a, b > 0, then
Well-known inequalities[edit]
Mathematicians often use inequalities to bound quantities for which exact formulas cannot be computed easily. Some inequalities are used so often that they have names:
- Azuma’s inequality
- Bernoulli’s inequality
- Bell’s inequality
- Boole’s inequality
- Cauchy–Schwarz inequality
- Chebyshev’s inequality
- Chernoff’s inequality
- Cramér–Rao inequality
- Hoeffding’s inequality
- Hölder’s inequality
- Inequality of arithmetic and geometric means
- Jensen’s inequality
- Kolmogorov’s inequality
- Markov’s inequality
- Minkowski inequality
- Nesbitt’s inequality
- Pedoe’s inequality
- Poincaré inequality
- Samuelson’s inequality
- Triangle inequality
Complex numbers and inequalities[edit]
The set of complex numbers ℂ with its operations of addition and multiplication is a field, but it is impossible to define any relation ≤ so that (C, +, ×, ≤) becomes an ordered field. To make (ℂ, +, ×, ≤) an ordered field, it would have to satisfy the following two properties:
- if a ≤ b, then a + c ≤ b + c;
- if 0 ≤ a and 0 ≤ b, then 0 ≤ ab.
Because ≤ is a total order, for any number a, either 0 ≤ a or a ≤ 0 (in which case the first property above implies that 0 ≤ −a). In either case 0 ≤ a2; this means that i2 > 0 and 12 > 0; so −1 > 0 and 1 > 0, which means (−1 + 1) > 0; contradiction.
However, an operation ≤ can be defined so as to satisfy only the first property (namely, «if a ≤ b, then a + c ≤ b + c«). Sometimes the lexicographical order definition is used:
- a ≤ b, if
- Re(a) < Re(b), or
- Re(a) = Re(b) and Im(a) ≤ Im(b)
It can easily be proven that for this definition a ≤ b implies a + c ≤ b + c.
Vector inequalities[edit]
Inequality relationships similar to those defined above can also be defined for column vectors. If we let the vectors 





Similarly, we can define relationships for 


The trichotomy property (as stated above) is not valid for vector relationships. For example, when 

Systems of inequalities[edit]
Systems of linear inequalities can be simplified by Fourier–Motzkin elimination.[15]
The cylindrical algebraic decomposition is an algorithm that allows testing whether a system of polynomial equations and inequalities has solutions, and, if solutions exist, describing them. The complexity of this algorithm is doubly exponential in the number of variables. It is an active research domain to design algorithms that are more efficient in specific cases.
See also[edit]
- Binary relation
- Bracket (mathematics), for the use of similar ‹ and › signs as brackets
- Inclusion (set theory)
- Inequation
- Interval (mathematics)
- List of inequalities
- List of triangle inequalities
- Partially ordered set
- Relational operators, used in programming languages to denote inequality
References[edit]
- ^ a b «Inequality Definition (Illustrated Mathematics Dictionary)». www.mathsisfun.com. Retrieved 2019-12-03.
- ^ a b «Inequality». www.learnalberta.ca. Retrieved 2019-12-03.
- ^ Polyanin, A.D.; Manzhirov, A.V. (2006). Handbook of Mathematics for Engineers and Scientists. CRC Press. p. 29. ISBN 978-1-4200-1051-0. Retrieved 2021-11-19.
- ^ Weisstein, Eric W. «Much Less». mathworld.wolfram.com. Retrieved 2019-12-03.
- ^ Weisstein, Eric W. «Much Greater». mathworld.wolfram.com. Retrieved 2019-12-03.
- ^ Drachman, Bryon C.; Cloud, Michael J. (2006). Inequalities: With Applications to Engineering. Springer Science & Business Media. pp. 2–3. ISBN 0-3872-2626-5.
- ^ «ProvingInequalities». www.cs.yale.edu. Retrieved 2019-12-03.
- ^ Simovici, Dan A. & Djeraba, Chabane (2008). «Partially Ordered Sets». Mathematical Tools for Data Mining: Set Theory, Partial Orders, Combinatorics. Springer. ISBN 9781848002012.
- ^ Weisstein, Eric W. «Partially Ordered Set». mathworld.wolfram.com. Retrieved 2019-12-03.
- ^ Feldman, Joel (2014). «Fields» (PDF). math.ubc.ca. Archived (PDF) from the original on 2022-10-09. Retrieved 2019-12-03.
- ^ Stewart, Ian (2007). Why Beauty Is Truth: The History of Symmetry. Hachette UK. p. 106. ISBN 978-0-4650-0875-9.
- ^ Brian W. Kernighan and Dennis M. Ritchie (Apr 1988). The C Programming Language. Prentice Hall Software Series (2nd ed.). Englewood Cliffs/NJ: Prentice Hall. ISBN 0131103628. Here: Sect.A.7.9 Relational Operators, p.167: Quote: «a<b<c is parsed as (a<b)<c»
- ^ Laub, M.; Ilani, Ishai (1990). «E3116». The American Mathematical Monthly. 97 (1): 65–67. doi:10.2307/2324012. JSTOR 2324012.
- ^ Manyama, S. (2010). «Solution of One Conjecture on Inequalities with Power-Exponential Functions» (PDF). Australian Journal of Mathematical Analysis and Applications. 7 (2): 1. Archived (PDF) from the original on 2022-10-09.
- ^ Gärtner, Bernd; Matoušek, Jiří (2006). Understanding and Using Linear Programming. Berlin: Springer. ISBN 3-540-30697-8.
Sources[edit]
- Hardy, G., Littlewood J. E., Pólya, G. (1999). Inequalities. Cambridge Mathematical Library, Cambridge University Press. ISBN 0-521-05206-8.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Beckenbach, E. F., Bellman, R. (1975). An Introduction to Inequalities. Random House Inc. ISBN 0-394-01559-2.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Drachman, Byron C., Cloud, Michael J. (1998). Inequalities: With Applications to Engineering. Springer-Verlag. ISBN 0-387-98404-6.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Grinshpan, A. Z. (2005), «General inequalities, consequences, and applications», Advances in Applied Mathematics, 34 (1): 71–100, doi:10.1016/j.aam.2004.05.001
- Murray S. Klamkin. «‘Quickie’ inequalities» (PDF). Math Strategies. Archived (PDF) from the original on 2022-10-09.
- Arthur Lohwater (1982). «Introduction to Inequalities». Online e-book in PDF format.
- Harold Shapiro (2005). «Mathematical Problem Solving». The Old Problem Seminar. Kungliga Tekniska högskolan.
- «3rd USAMO». Archived from the original on 2008-02-03.
- Pachpatte, B. G. (2005). Mathematical Inequalities. North-Holland Mathematical Library. Vol. 67 (first ed.). Amsterdam, The Netherlands: Elsevier. ISBN 0-444-51795-2. ISSN 0924-6509. MR 2147066. Zbl 1091.26008.
- Ehrgott, Matthias (2005). Multicriteria Optimization. Springer-Berlin. ISBN 3-540-21398-8.
- Steele, J. Michael (2004). The Cauchy-Schwarz Master Class: An Introduction to the Art of Mathematical Inequalities. Cambridge University Press. ISBN 978-0-521-54677-5.
External links[edit]
- «Inequality», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Graph of Inequalities by Ed Pegg, Jr.
- AoPS Wiki entry about Inequalities
This article is about relations «greater than» and «less than». For the relation «not equal», see Inequation.
In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions.[1] It is used most often to compare two numbers on the number line by their size. There are several different notations used to represent different kinds of inequalities:
- The notation a < b means that a is less than b.
- The notation a > b means that a is greater than b.
In either case, a is not equal to b. These relations are known as strict inequalities,[1] meaning that a is strictly less than or strictly greater than b. Equivalence is excluded.
In contrast to strict inequalities, there are two types of inequality relations that are not strict:
- The notation a ≤ b or a ⩽ b means that a is less than or equal to b (or, equivalently, at most b, or not greater than b).
- The notation a ≥ b or a ⩾ b means that a is greater than or equal to b (or, equivalently, at least b, or not less than b).
The relation not greater than can also be represented by a ≯ b, the symbol for «greater than» bisected by a slash, «not». The same is true for not less than and a ≮ b.
The notation a ≠ b means that a is not equal to b; this inequation sometimes is considered a form of strict inequality.[2] It does not say that one is greater than the other; it does not even require a and b to be member of an ordered set.
In engineering sciences, less formal use of the notation is to state that one quantity is «much greater» than another,[3] normally by several orders of magnitude.
- The notation a ≪ b means that a is much less than b.[4]
- The notation a ≫ b means that a is much greater than b.[5]
This implies that the lesser value can be neglected with little effect on the accuracy of an approximation (such as the case of ultrarelativistic limit in physics).
In all of the cases above, any two symbols mirroring each other are symmetrical; a < b and b > a are equivalent, etc.
Properties on the number line[edit]
Inequalities are governed by the following properties. All of these properties also hold if all of the non-strict inequalities (≤ and ≥) are replaced by their corresponding strict inequalities (< and >) and — in the case of applying a function — monotonic functions are limited to strictly monotonic functions.
Converse[edit]
The relations ≤ and ≥ are each other’s converse, meaning that for any real numbers a and b:
a ≤ b and b ≥ a are equivalent.
Transitivity[edit]
The transitive property of inequality states that for any real numbers a, b, c:[6]
If a ≤ b and b ≤ c, then a ≤ c.
If either of the premises is a strict inequality, then the conclusion is a strict inequality:
If a ≤ b and b < c, then a < c.
If a < b and b ≤ c, then a < c.
Addition and subtraction[edit]
If x < y, then x + a < y + a.
A common constant c may be added to or subtracted from both sides of an inequality.[2] So, for any real numbers a, b, c:
If a ≤ b, then a + c ≤ b + c and a − c ≤ b − c.
In other words, the inequality relation is preserved under addition (or subtraction) and the real numbers are an ordered group under addition.
Multiplication and division[edit]
If x < y and a > 0, then ax < ay.
If x < y and a < 0, then ax > ay.
The properties that deal with multiplication and division state that for any real numbers, a, b and non-zero c:
If a ≤ b and c > 0, then ac ≤ bc and a/c ≤ b/c.
If a ≤ b and c < 0, then ac ≥ bc and a/c ≥ b/c.
In other words, the inequality relation is preserved under multiplication and division with positive constant, but is reversed when a negative constant is involved. More generally, this applies for an ordered field. For more information, see § Ordered fields.
Additive inverse[edit]
The property for the additive inverse states that for any real numbers a and b:
If a ≤ b, then −a ≥ −b.
Multiplicative inverse[edit]
If both numbers are positive, then the inequality relation between the multiplicative inverses is opposite of that between the original numbers. More specifically, for any non-zero real numbers a and b that are both positive (or both negative):
If a ≤ b, then 1/a ≥
1/b.
All of the cases for the signs of a and b can also be written in chained notation, as follows:
If 0 < a ≤ b, then
1/a ≥
1/b > 0.
If a ≤ b < 0, then 0 >
1/a ≥
1/b.
If a < 0 < b, then
1/a < 0 <
1/b.
Applying a function to both sides[edit]
Any monotonically increasing function, by its definition,[7] may be applied to both sides of an inequality without breaking the inequality relation (provided that both expressions are in the domain of that function). However, applying a monotonically decreasing function to both sides of an inequality means the inequality relation would be reversed. The rules for the additive inverse, and the multiplicative inverse for positive numbers, are both examples of applying a monotonically decreasing function.
If the inequality is strict (a < b, a > b) and the function is strictly monotonic, then the inequality remains strict. If only one of these conditions is strict, then the resultant inequality is non-strict. In fact, the rules for additive and multiplicative inverses are both examples of applying a strictly monotonically decreasing function.
A few examples of this rule are:
- Raising both sides of an inequality to a power n > 0 (equiv., −n < 0), when a and b are positive real numbers:
0 ≤ a ≤ b ⇔ 0 ≤ an ≤ bn.
0 ≤ a ≤ b ⇔ a−n ≥ b−n ≥ 0.
- Taking the natural logarithm on both sides of an inequality, when a and b are positive real numbers:
0 < a ≤ b ⇔ ln(a) ≤ ln(b).
0 < a < b ⇔ ln(a) < ln(b).
(this is true because the natural logarithm is a strictly increasing function.)
Formal definitions and generalizations[edit]
A (non-strict) partial order is a binary relation ≤ over a set P which is reflexive, antisymmetric, and transitive.[8] That is, for all a, b, and c in P, it must satisfy the three following clauses:
- a ≤ a (reflexivity)
- if a ≤ b and b ≤ a, then a = b (antisymmetry)
- if a ≤ b and b ≤ c, then a ≤ c (transitivity)
A set with a partial order is called a partially ordered set.[9] Those are the very basic axioms that every kind of order has to satisfy. Other axioms that exist for other definitions of orders on a set P include:
- For every a and b in P, a ≤ b or b ≤ a (total order).
- For all a and b in P for which a < b, there is a c in P such that a < c < b (dense order).
- Every non-empty subset of P with an upper bound has a least upper bound (supremum) in P (least-upper-bound property).
Ordered fields[edit]
If (F, +, ×) is a field and ≤ is a total order on F, then (F, +, ×, ≤) is called an ordered field if and only if:
- a ≤ b implies a + c ≤ b + c;
- 0 ≤ a and 0 ≤ b implies 0 ≤ a × b.
Both (Q, +, ×, ≤) and (R, +, ×, ≤) are ordered fields, but ≤ cannot be defined in order to make (C, +, ×, ≤) an ordered field,[10] because −1 is the square of i and would therefore be positive.
Besides from being an ordered field, R also has the Least-upper-bound property. In fact, R can be defined as the only ordered field with that quality.[11]
Chained notation[edit]
The notation a < b < c stands for «a < b and b < c«, from which, by the transitivity property above, it also follows that a < c. By the above laws, one can add or subtract the same number to all three terms, or multiply or divide all three terms by same nonzero number and reverse all inequalities if that number is negative. Hence, for example, a < b + e < c is equivalent to a − e < b < c − e.
This notation can be generalized to any number of terms: for instance, a1 ≤ a2 ≤ … ≤ an means that ai ≤ ai+1 for i = 1, 2, …, n − 1. By transitivity, this condition is equivalent to ai ≤ aj for any 1 ≤ i ≤ j ≤ n.
When solving inequalities using chained notation, it is possible and sometimes necessary to evaluate the terms independently. For instance, to solve the inequality 4x < 2x + 1 ≤ 3x + 2, it is not possible to isolate x in any one part of the inequality through addition or subtraction. Instead, the inequalities must be solved independently, yielding x < 1/2 and x ≥ −1 respectively, which can be combined into the final solution −1 ≤ x < 1/2.
Occasionally, chained notation is used with inequalities in different directions, in which case the meaning is the logical conjunction of the inequalities between adjacent terms. For example, the defining condition of a zigzag poset is written as a1 < a2 > a3 < a4 > a5 < a6 > … . Mixed chained notation is used more often with compatible relations, like <, =, ≤. For instance, a < b = c ≤ d means that a < b, b = c, and c ≤ d. This notation exists in a few programming languages such as Python. In contrast, in programming languages that provide an ordering on the type of comparison results, such as C, even homogeneous chains may have a completely different meaning.[12]
Sharp inequalities[edit]
An inequality is said to be sharp if it cannot be relaxed and still be valid in general. Formally, a universally quantified inequality φ is called sharp if, for every valid universally quantified inequality ψ, if ψ ⇒ φ holds, then ψ ⇔ φ also holds. For instance, the inequality ∀a ∈ R. a2 ≥ 0 is sharp, whereas the inequality ∀a ∈ R. a2 ≥ −1 is not sharp.[citation needed]
Inequalities between means[edit]
There are many inequalities between means. For example, for any positive numbers a1, a2, …, an we have H ≤ G ≤ A ≤ Q, where they represent the following means of the sequence:
- Harmonic mean
- Geometric mean
- Arithmetic mean
- quadratic mean
Cauchy–Schwarz inequality[edit]
The Cauchy–Schwarz inequality states that for all vectors u and v of an inner product space it is true that
where 
Power inequalities[edit]
A «power inequality» is an inequality containing terms of the form ab, where a and b are real positive numbers or variable expressions. They often appear in mathematical olympiads exercises.
Examples[edit]
- For any real x,
- If x > 0 and p > 0, then
In the limit of p → 0, the upper and lower bounds converge to ln(x).
- If x > 0, then
- If x > 0, then
- If x, y, z > 0, then
- For any real distinct numbers a and b,
- If x, y > 0 and 0 < p < 1, then
- If x, y, z > 0, then
- If a, b > 0, then[13]
- If a, b > 0, then[14]
- If a, b, c > 0, then
- If a, b > 0, then
Well-known inequalities[edit]
Mathematicians often use inequalities to bound quantities for which exact formulas cannot be computed easily. Some inequalities are used so often that they have names:
- Azuma’s inequality
- Bernoulli’s inequality
- Bell’s inequality
- Boole’s inequality
- Cauchy–Schwarz inequality
- Chebyshev’s inequality
- Chernoff’s inequality
- Cramér–Rao inequality
- Hoeffding’s inequality
- Hölder’s inequality
- Inequality of arithmetic and geometric means
- Jensen’s inequality
- Kolmogorov’s inequality
- Markov’s inequality
- Minkowski inequality
- Nesbitt’s inequality
- Pedoe’s inequality
- Poincaré inequality
- Samuelson’s inequality
- Triangle inequality
Complex numbers and inequalities[edit]
The set of complex numbers ℂ with its operations of addition and multiplication is a field, but it is impossible to define any relation ≤ so that (C, +, ×, ≤) becomes an ordered field. To make (ℂ, +, ×, ≤) an ordered field, it would have to satisfy the following two properties:
- if a ≤ b, then a + c ≤ b + c;
- if 0 ≤ a and 0 ≤ b, then 0 ≤ ab.
Because ≤ is a total order, for any number a, either 0 ≤ a or a ≤ 0 (in which case the first property above implies that 0 ≤ −a). In either case 0 ≤ a2; this means that i2 > 0 and 12 > 0; so −1 > 0 and 1 > 0, which means (−1 + 1) > 0; contradiction.
However, an operation ≤ can be defined so as to satisfy only the first property (namely, «if a ≤ b, then a + c ≤ b + c«). Sometimes the lexicographical order definition is used:
- a ≤ b, if
- Re(a) < Re(b), or
- Re(a) = Re(b) and Im(a) ≤ Im(b)
It can easily be proven that for this definition a ≤ b implies a + c ≤ b + c.
Vector inequalities[edit]
Inequality relationships similar to those defined above can also be defined for column vectors. If we let the vectors 





Similarly, we can define relationships for 


The trichotomy property (as stated above) is not valid for vector relationships. For example, when 

Systems of inequalities[edit]
Systems of linear inequalities can be simplified by Fourier–Motzkin elimination.[15]
The cylindrical algebraic decomposition is an algorithm that allows testing whether a system of polynomial equations and inequalities has solutions, and, if solutions exist, describing them. The complexity of this algorithm is doubly exponential in the number of variables. It is an active research domain to design algorithms that are more efficient in specific cases.
See also[edit]
- Binary relation
- Bracket (mathematics), for the use of similar ‹ and › signs as brackets
- Inclusion (set theory)
- Inequation
- Interval (mathematics)
- List of inequalities
- List of triangle inequalities
- Partially ordered set
- Relational operators, used in programming languages to denote inequality
References[edit]
- ^ a b «Inequality Definition (Illustrated Mathematics Dictionary)». www.mathsisfun.com. Retrieved 2019-12-03.
- ^ a b «Inequality». www.learnalberta.ca. Retrieved 2019-12-03.
- ^ Polyanin, A.D.; Manzhirov, A.V. (2006). Handbook of Mathematics for Engineers and Scientists. CRC Press. p. 29. ISBN 978-1-4200-1051-0. Retrieved 2021-11-19.
- ^ Weisstein, Eric W. «Much Less». mathworld.wolfram.com. Retrieved 2019-12-03.
- ^ Weisstein, Eric W. «Much Greater». mathworld.wolfram.com. Retrieved 2019-12-03.
- ^ Drachman, Bryon C.; Cloud, Michael J. (2006). Inequalities: With Applications to Engineering. Springer Science & Business Media. pp. 2–3. ISBN 0-3872-2626-5.
- ^ «ProvingInequalities». www.cs.yale.edu. Retrieved 2019-12-03.
- ^ Simovici, Dan A. & Djeraba, Chabane (2008). «Partially Ordered Sets». Mathematical Tools for Data Mining: Set Theory, Partial Orders, Combinatorics. Springer. ISBN 9781848002012.
- ^ Weisstein, Eric W. «Partially Ordered Set». mathworld.wolfram.com. Retrieved 2019-12-03.
- ^ Feldman, Joel (2014). «Fields» (PDF). math.ubc.ca. Archived (PDF) from the original on 2022-10-09. Retrieved 2019-12-03.
- ^ Stewart, Ian (2007). Why Beauty Is Truth: The History of Symmetry. Hachette UK. p. 106. ISBN 978-0-4650-0875-9.
- ^ Brian W. Kernighan and Dennis M. Ritchie (Apr 1988). The C Programming Language. Prentice Hall Software Series (2nd ed.). Englewood Cliffs/NJ: Prentice Hall. ISBN 0131103628. Here: Sect.A.7.9 Relational Operators, p.167: Quote: «a<b<c is parsed as (a<b)<c»
- ^ Laub, M.; Ilani, Ishai (1990). «E3116». The American Mathematical Monthly. 97 (1): 65–67. doi:10.2307/2324012. JSTOR 2324012.
- ^ Manyama, S. (2010). «Solution of One Conjecture on Inequalities with Power-Exponential Functions» (PDF). Australian Journal of Mathematical Analysis and Applications. 7 (2): 1. Archived (PDF) from the original on 2022-10-09.
- ^ Gärtner, Bernd; Matoušek, Jiří (2006). Understanding and Using Linear Programming. Berlin: Springer. ISBN 3-540-30697-8.
Sources[edit]
- Hardy, G., Littlewood J. E., Pólya, G. (1999). Inequalities. Cambridge Mathematical Library, Cambridge University Press. ISBN 0-521-05206-8.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Beckenbach, E. F., Bellman, R. (1975). An Introduction to Inequalities. Random House Inc. ISBN 0-394-01559-2.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Drachman, Byron C., Cloud, Michael J. (1998). Inequalities: With Applications to Engineering. Springer-Verlag. ISBN 0-387-98404-6.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Grinshpan, A. Z. (2005), «General inequalities, consequences, and applications», Advances in Applied Mathematics, 34 (1): 71–100, doi:10.1016/j.aam.2004.05.001
- Murray S. Klamkin. «‘Quickie’ inequalities» (PDF). Math Strategies. Archived (PDF) from the original on 2022-10-09.
- Arthur Lohwater (1982). «Introduction to Inequalities». Online e-book in PDF format.
- Harold Shapiro (2005). «Mathematical Problem Solving». The Old Problem Seminar. Kungliga Tekniska högskolan.
- «3rd USAMO». Archived from the original on 2008-02-03.
- Pachpatte, B. G. (2005). Mathematical Inequalities. North-Holland Mathematical Library. Vol. 67 (first ed.). Amsterdam, The Netherlands: Elsevier. ISBN 0-444-51795-2. ISSN 0924-6509. MR 2147066. Zbl 1091.26008.
- Ehrgott, Matthias (2005). Multicriteria Optimization. Springer-Berlin. ISBN 3-540-21398-8.
- Steele, J. Michael (2004). The Cauchy-Schwarz Master Class: An Introduction to the Art of Mathematical Inequalities. Cambridge University Press. ISBN 978-0-521-54677-5.
External links[edit]
- «Inequality», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Graph of Inequalities by Ed Pegg, Jr.
- AoPS Wiki entry about Inequalities












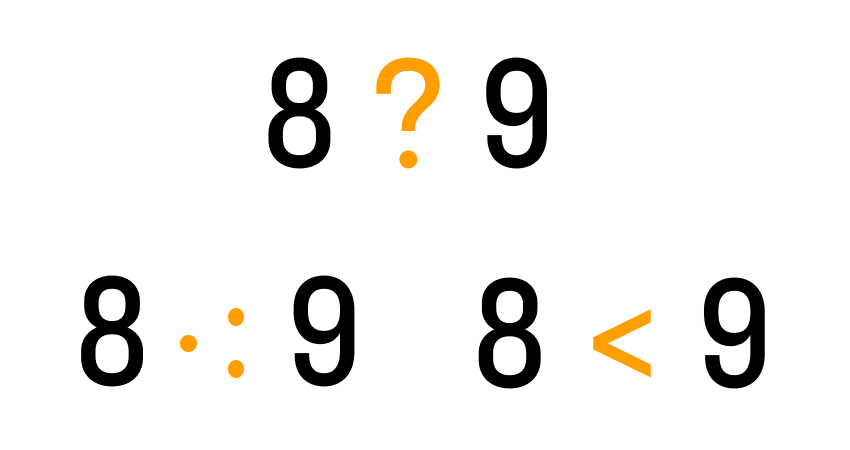



















![G={sqrt[{n}]{a_{1}cdot a_{2}cdots a_{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4d9a1963e82d8495a2d8fb86f6c52f5150a262c)















