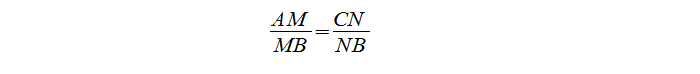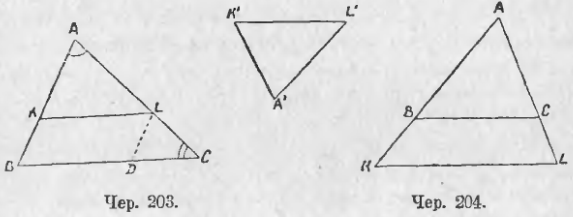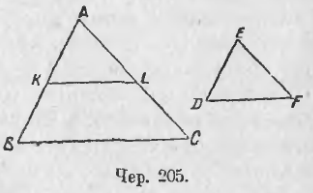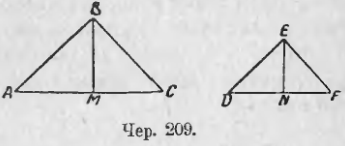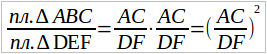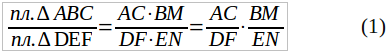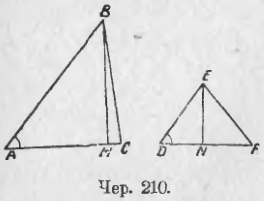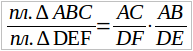В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.
Определение и знак подобия в геометрии
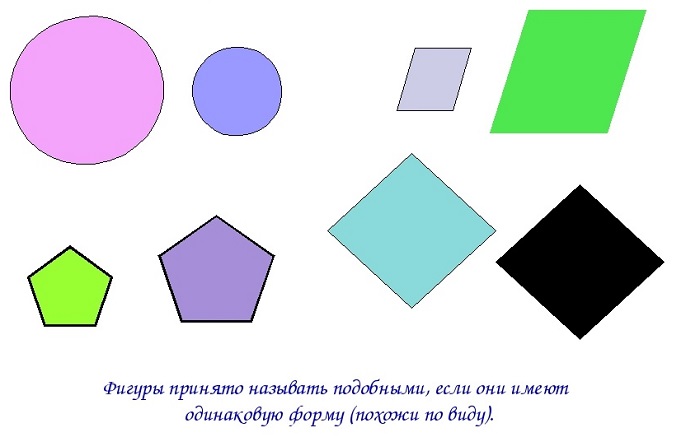
Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.
Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:
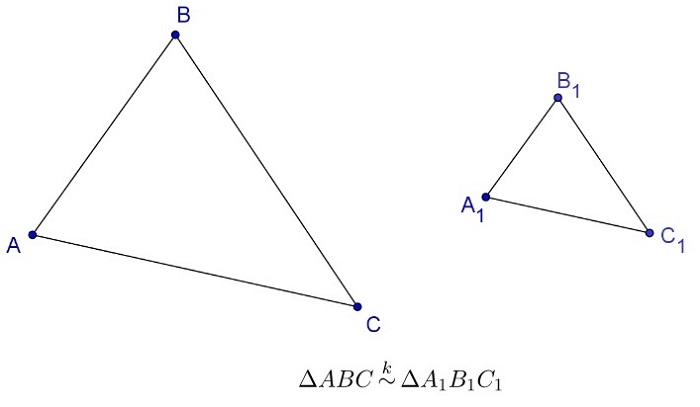
∆ABC ~ ∆A1B1C1
— треугольники ABC и A1B1C1
подобны.
Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:
1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Коэффициент подобия треугольников и знак подобия
Часто сверху знака подобия выставляют коэффициент подобия треугольников:
В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.
В алгебре высказываний знаком ~ обозначают логическую операцию «эквиваленция».
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):
Признаки подобия прямоугольных треугольников
Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.
Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.
Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.
Утверждения:
-
треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;
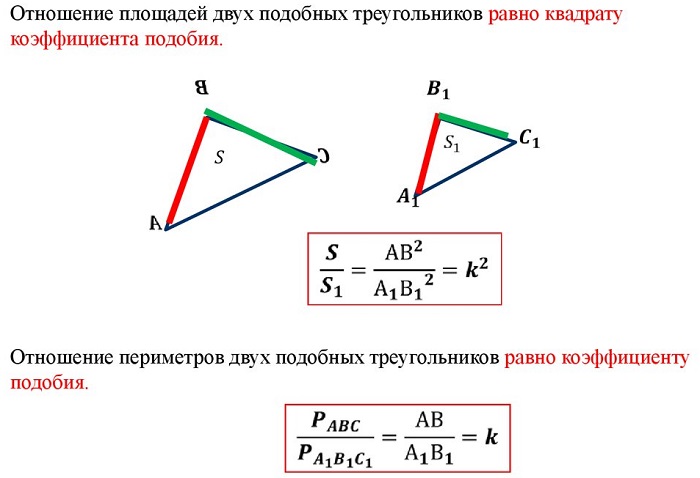
-
отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство подобия треугольников через среднюю линию
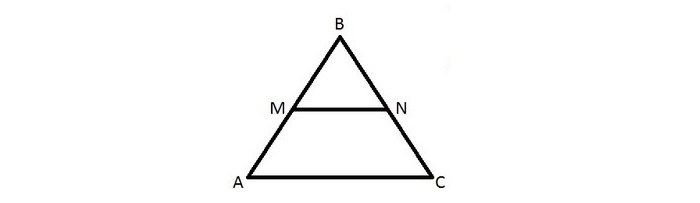
Имеется треугольник ∆ABC, mn — средняя линия. M лежит на AB, N лежит на BC.
Требуется доказательство подобия треугольников ∆MBN и ∆ABC.
Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:
Отсюда делаем вывод, что ∆MBN ~ ∆ABC по II признаку подобия треугольников, что и требовалось доказать.
Примеры решения задач по геометрии на тему «Подобие треугольников»
_____________________________________________________________________
Подобные треугольники в евклидовой геометрии — треугольники, углы у которых соответственно равны, а стороны соответственно пропорциональны. Являются подобными фигурами.
В данной статье рассматриваются свойства подобных треугольников в евклидовой геометрии. Некоторые утверждения являются неверными для неевклидовых геометрий.
Признаки подобия треугольников[править | править код]
Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов определения.
Первый признак[править | править код]
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.
то есть:
Дано: и
Доказать:
Следствия первого признака подобия[править | править код]
- Если три разные стороны исходного треугольника попарно параллельны (дважды антипараллельны или перпендикулярны) трем разным сходственным сторонам другого треугольника, то указанные два треугольника подобны. Примеры применения этого следствия см. ниже в разделах: «Примеры подобных треугольников» и «Свойства параллельности (антипараллельности) сторон родственных треугольников».
- Под дважды антипараллельными сторонами понимается следующее. Например, стороны данного остроугольного треугольника антипараллельны соответствующим сторонам ортотреугольника, против которых они лежат. В таком случае соответствующие стороны ортотреугольника ортотреугольника (дважды ортотреугольника) дважды антипараллельны соответствующим сторонам исходного треугольника, то есть просто параллельны. Следовательно, подобны, например, ортотреугольник ортотреугольника и исходный треугольник как треугольники с параллельными сторонами.
Второй признак[править | править код]
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Дано: и
Доказать:
Третий признак[править | править код]
Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то такие треугольники подобны.
Дано: и = = .
Доказать:
Признаки подобия прямоугольных треугольников[править | править код]
- По острому углу — см. первый признак;
- По двум катетам — см. второй признак;
- По катету и гипотенузе — см. третий признак.
Свойства подобных треугольников[править | править код]
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия
- Отношение периметров и длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия.
Примеры подобных треугольников[править | править код]
Подобны следующие виды треугольников:
- Дополнительный треугольник и антидополнительный треугольник подобны; соответственные их стороны параллельны.
- Треугольник ABC подобен своему дополнительному треугольнику; соответственные их стороны параллельны и относятся как 2:1.
- Треугольник ABC подобен своему антидополнительному треугольнику; соответственные их стороны параллельны и относятся как 1:2.
- Исходный треугольник по отношению к ортотреугольнику является треугольником трёх внешних биссектрис[1].
- Ортотреугольник и тангенциальный треугольник подобны (Зетель, следствие 1, § 66, с. 81).
- Ортотреугольник ортотреугольника и исходный треугольник подобны.
- Треугольник трёх внешних биссектрис треугольника трех внешних биссектрис и исходный треугольник подобны.
- Пусть точки касания вписанной в данный треугольник окружности соединены отрезками, тогда получится треугольник Жергонна, и в полученном треугольнике проведены высоты. В этом случае прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно ортотреугольник треугольника Жергонна и исходный треугольник подобны.
- Выше указанные свойства подобия родственных треугольников являются следствием ниже перечисленных свойств параллельности сторон родственных треугольников.
- Теорема: окружностно-чевианный треугольник подобен подерному[2]. Здесь использованы определения:
- Треугольник с вершинами во вторых точках пересечения прямых, проведённых через вершины и данную точку, с описанной окружностью, называют окружностно-чевианным треугольником.
- Треугольник с вершинами в проекциях данной точки на стороны называется подерным или педальным треугольником этой точки.
Свойства параллельности (антипараллельности) сторон родственных треугольников[править | править код]
- Соответственные стороны дополнительного треугольника, антидополнительного треугольника и исходного треугольника попарно параллельны.
- Стороны данного остроугольного треугольника антипараллельны соответствующим сторонам ортотреугольника, против которых они лежат.
- Стороны тангенциального треугольника антипараллельны соответствующим противоположным сторонам данного треугольника (по свойству антипараллельности касательных к окружности).
- Стороны тангенциального треугольника параллельны соответствующим сторонам ортотреугольника.
- Пусть точки касания вписанной в данный треугольник окружности соединены отрезками, тогда получится треугольник Жергонна, и в полученном треугольнике проведены высоты. В этом случае прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно ортотреугольник треугольника Жергонна и исходный треугольник подобны.
Подобие в прямоугольном треугольнике[править | править код]
Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:
- Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому проекций катетов на гипотенузу,
- Катет равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу.
Связанные определения[править | править код]
- Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
- Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.
См. также[править | править код]
- Неравенство Пидо
- Подобие
- Признаки равенства треугольников
- Решение треугольников
- Среднее геометрическое
- Треугольник
Примечания[править | править код]
- ↑ Стариков В. Н. Исследования по геометрии// Сборник публикаций научного журнала Globus по материалам V-й международной научно-практической конференции «Достижения и проблемы современной науки» г. Санкт-Петербург: сборник со статьями (уровень стандарта, академический уровень). С-П.: Научный журнал Globus, 2016. С. 99-100
- ↑ Система задач по геометрии Р. К. Гордина. Задача 6480. Дата обращения: 26 апреля 2016. Архивировано 4 марта 2016 года.
Литература[править | править код]
- Геометрия 7-9/Л. С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.:
- Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. 153 с.
Ссылки[править | править код]
- Видео. Подобные треугольники
- Подобие треугольников
- Признаки подобия из учебника за восьмой класс
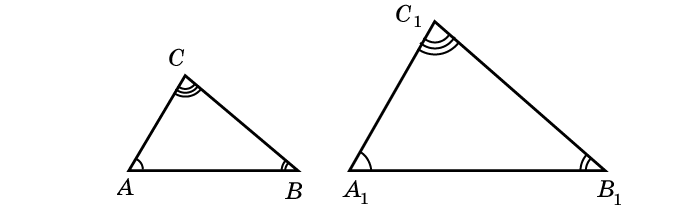
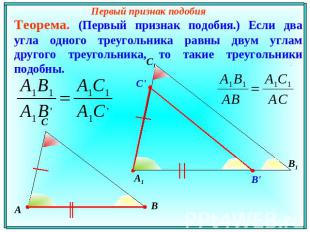
Теорема 1. Первый признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого, то такие
треугольники подобны.
Доказательство. Пусть ABC и $А_1В_1С_1$ — треугольники, у которых $angle A = angle A_1 ; angle B = angle B_1$ , и, следовательно, $angle C = angle C_1$ . Докажем, что $triangle ABC sim triangle A_1B_1C_1$ (рис.1).
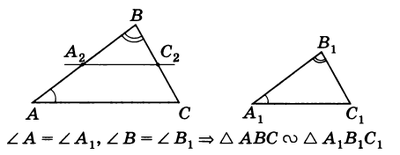
Рис.1
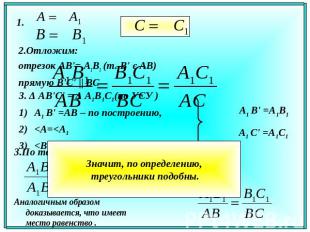
Отложим на ВА от точки В отрезок $ВА_2$, равный отрезку $A_1B_1$ , и через точку $А_2$ проведем прямую, параллельную прямой АС. Эта прямая пересечет ВС в некоторой точке $С_2$ . Треугольники $А_1В_1С_1text{ и }А_2ВС_2$ равны: $А_1В_1 = А_2В$ по построению, $angle В = angle В_1$ по условию и $angle А_1 = angle А_2$ , так как $angle А_1 = angle А$ по условию и $angle А = angle А_2$ как соответственные углы. По лемме 1 о подобных треугольниках имеем: $triangle A_2BC_2 sim triangle ABC$ , и значит, $triangle ABC sim triangle A_1B_1C_1$ . Теорема доказана.
По аналогичной схеме устанавливаются теоремы 2 и 3.
Теорема 2. Второй признак подобия треугольников. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы между этими сторонами
равны, то треугольники подобны.
Теорема 3. Третий признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Из теоремы 1 вытекает следующее.
Следствие 1. В подобных треугольниках сходственные стороны пропорциональны сходственным высотам, т. е. тем высотам, которые опущены на сходственные стороны.
Пример 1. Подобны ли два равносторонних треугольника?
Решение. Так как в равностороннем треугольнике каждый внутренний угол равен 60° (следствие 3), то два равносторонних треугольника подобны по первому признаку.
Пример 2. В треугольниках ABC и $А_1В_1С_1$ известно, что $angle A = angle A_1 ; angle B = angle B_1 ; АВ = 5 м, ВС = 7 м, А_1В_1 = 10 м, А_1С_1 = 8 м.$ Найти неизвестные стороны треугольников.
Решение. Треугольники, определенные условием задачи, подобны по первому признаку подобия.
Из подобия треугольников следует:
$$ frac{AB}{A_1B_1} = frac{BC}{B_1C_1} = frac{AC}{A_1C_1} ,,, (1) $$
Подставив в равенство (1) данные из условия задачи, получим:
$$ frac{5}{10} = frac{7}{B_1C_1} = frac{AC}{8} ,,, (2) $$
Из равенства (2) составим две пропорции
$$ frac{5}{10} = frac{7}{B_1C_1}
frac{5}{10} = frac{AC}{8}
text{ откуда }В_1С_1 = 14 (м), АС = 4 (м).
$$
Пример 3. Углы В и $В_1$ треугольников ABC и $А_1В_1С_1$ равны. Стороны АВ и ВС треугольника ABC в 2,5 раза больше сторон $A_1B_1$ и $B_1C_1$ треугольника $A_1B_1C_1$. Найти АС и $A_1C_1$ , если их сумма равна 4,2 м.
Решение. Пусть условию задачи отвечает рисунок 2.
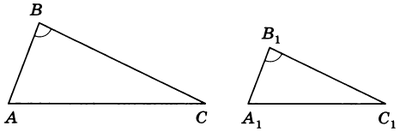
Рис.2
Из условия задачи:
$$ 1) angle B = angle B_1 ;
2) frac{AB}{A_1B_1} = frac{BC}{B_1C_1} = 2,5
3) AC + A_1C_1 = 4,2 м.
$$
Следовательно, $triangle ABC sim triangle А_1В_1С_1$. Из подобия этих треугольников следует
$$ frac{AC}{A_1C_1} = 2,5text{ , или }АС = 2,5bullet А_1С_1 $$
Так как АС = 2,5 • А1С1, то АС + А1C1 = 2,5 • А1С1 + A1C1 = 4,2, откуда A1C1 = 1,2 (м), АС = 3 (м).
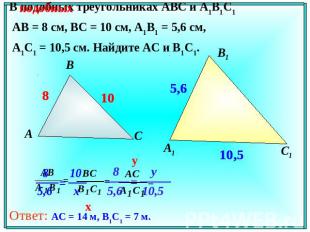
Пример 4. Подобны ли треугольники ABC и А1В1С1, если АВ = 3 см, ВС = 5 см, АС = 7 см, А1В1 = 4,5 см, B1C1 = 7,5 см, A1C1 = 10,5 см?
Решение. Имеем:
$$ frac{AB}{A_1B_1} = frac{3}{4,5} = frac{1}{1,5}
frac{BC}{B_1C_1} = frac{5}{7,5} = frac{1}{1,5}
frac{AC}{A_1C_1} = frac{7}{10,5} = frac{1}{1,5}
$$
Следовательно, треугольники подобны по третьему признаку.
Пример 5. Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Решение. Рассмотрим произвольный треугольник ABC. Обозначим буквой О точку пересечения его медиан $АА_1text{ и }ВВ_1$ и проведем среднюю линию $A_1B_1$ этого треугольника (рис.3).
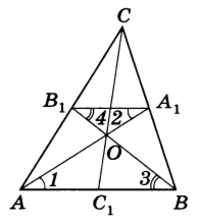
Рис.3
Отрезок $A_1B_1$ параллелен стороне АВ, поэтому $angle 1 = angle2 text{ и } angle 3 = angle 4 $. Следовательно, треугольники АОВ и $A_1OB_1$ подобны по двум углам, и, значит, их стороны пропорциональны:
$$ frac{AO}{A_1O} = frac{BO}{B_1O} = frac{AB}{A_1B_1} $$
Но $AB = 2A_1B_1$ , поэтому $AO = 2A_1O$ и $BO = 2B_1O$ .
Аналогично доказывается, что точка пересечения медиан $BB_1text{ и }CC_1} делит каждую из них в отношении 2:1, считая от вершины, и, следовательно, совпадает с точкой О.
Итак, все три медианы треугольника ABC пересекаются в точке О и делятся ею в отношении 2:1, считая от вершины.
Замечание. Ранее отмечалось, что биссектрисы треугольника пересекаются в одной точке, серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. На основе последнего утверждения устанавливается, что и высоты треугольника (или их продолжения) пересекаются в одной точке. Эти три точки и точка пересечения медиан называются замечательными точками треугольника.
Пример 6. Проектор полностью освещает экран А высотой 90 см, расположенный на расстоянии 240 см. На каком наименьшем расстоянии в см. от проектора нужно расположить экран Б, высотой 150 см, так, что бы он был полностью освещён, если настройки проектора остаются неизменными.
Видео-решение.
Презентация на тему: Подобие треугольников. Первый признак подобия
Скачать эту презентацию
Скачать эту презентацию
№ слайда 1

Описание слайда:
Подобие треугольников.Первый признак подобия
№ слайда 2

Описание слайда:
Изобразим: а) две неравные окружности; б) два неравных квадрата; в) два неравных равнобедренных прямоугольных треугольника; г) два неравных равносторонних треугольника.Чем отличаются фигуры в каждой представленной паре? Что у них общего? Почему они не равны?
№ слайда 3

Описание слайда:
Определение. Два треугольника называются подобными, если углы одного соответственно равны углам другого и соответствующие стороны пропорциональны. Коэффициент пропорциональности называется коэффициентом подобия.
№ слайда 4

Описание слайда:
Что значит, что Δ АВС подобен треугольнику Δ A1В1С1? Для своих изображенных пар фигур определите их коэффициент подобия.
№ слайда 5
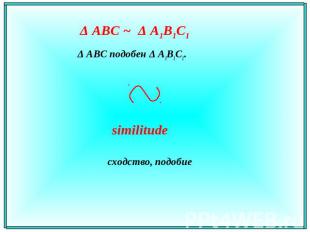
Описание слайда:
Δ АВС ~ Δ A1В1С1 Δ АВС подобен Δ A1В1С1. similitudeсходство, подобие
№ слайда 6

Описание слайда:
Укажите пропорциональные стороны
№ слайда 7
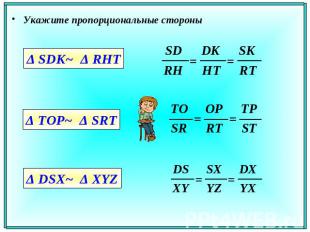
Описание слайда:
Укажите пропорциональные стороны
№ слайда 8

Описание слайда:
Стороны треугольника равны 5 см, 8 см и 10 см. Найдите стороны подобного ему треугольника, если коэффициент подобия равен: а) 0,5; б) 2.
№ слайда 9
Описание слайда:
В подобных треугольниках АВС и А1В1С1 АВ = 8 см, ВС = 10 см, А1В1 = 5,6 см, А1С1 = 10,5 см. Найдите АС и В1С1.
№ слайда 10

Описание слайда:
– Пройдите глазами по знаку подобия.– Закройте глаза. – Расслабьте мышцы лба.– Медленно переведите глазные яблоки в крайнее левое положение.– Почувствуйте напряжение глазных мышц.– Зафиксируйте положение– Теперь медленно с напряжением переведите глаза вправо.– Повторите четыре раза.– Откройте глаза.– Пройдите глазами по знаку подобия.
№ слайда 11
Описание слайда:
Первый признак подобия Теорема. (Первый признак подобия.) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
№ слайда 12

Описание слайда:
Теорема. (Первый признак подобия треугольников.) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
№ слайда 13
Описание слайда:
Значит, по определению, треугольники подобны. Аналогичным образом доказывается, что имеет место равенство .
№ слайда 14

Описание слайда:
Подобны ли прямоугольные треугольники, если у одного из них есть угол 40о, а у другого 50о?Два треугольника подобны. Два угла одного треугольника равны 55о и 80о. Найдите наименьший угол второго треугольника.
№ слайда 15
Описание слайда:
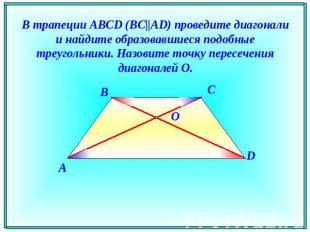
В трапеции ABCD (BC||AD) проведите диагонали и найдите образовавшиеся подобные треугольники. Назовите точку пересечения диагоналей O.
Знак подобия в геометрии — правило и примеры обозначения
На чтение 2 мин Просмотров 226
В учебниках по геометрии часто встречаются задачи на подобие фигур. Какой знак используется для обозначения подобия фигур? Какие фигуры называются подобными? Поговорим обо всем этом в нашей статье.
Определение и знак подобия в геометрии
Подобными называются фигуры, если одна из них представляет уменьшенную копию другой.
На нижеприведенном рисунке подобные фигуры: круги, параллелограммы, пятиугольники и ромбы.
Для обозначения термина «подобие» в геометрии используют знак «тильда», который является типографским символом и обозначается волнистой чертой:
∆ABC ~ ∆A1B1C1
— треугольники ABC и A1B1C1
подобны.
Знак «двойная тильда» ставится около чисел для демонстрации примерности или приблизительности чего-либо:
1,35 ≈ 1,4 — числа 1,35 и 1,4 приблизительно равны.
Коэффициент подобия треугольников и знак подобия
Часто сверху знака подобия выставляют коэффициент подобия треугольников:
В математических задачах и уравнениях «тильду» используют для маркирования разных типов подобия. Часто применяется для обозначения подобия, эквивалентности.
В алгебре высказываний знаком ~ обозначают логическую операцию «эквиваленция».
При сочетании тильды и знака равенства получают обозначение отношения конгруэнтности, определения в геометрии, применяемого в контексте обозначения равенства различных фигур и тел (углов, отрезков):
Признаки подобия прямоугольных треугольников
Острые углы: наличие равного острого угла в прямоугольных треугольниках делает их подобными.
Два катета: общая пропорциональность катетам одного прямоугольного треугольника к катетам второго делает их подобными.
Катет и гипотенуза: пропорциональность катета и гипотенузы одного прямоугольного треугольника к катету и гипотенузе второго прямоугольного треугольника делает их подобными.
Утверждения:
-
треугольник ∆ABC и треугольник ∆A1B1C1 считаются подобными при равнозначности углов и пропорциональности сторон;
-
отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство подобия треугольников через среднюю линию
Имеется треугольник ∆ABC, mn — средняя линия. M лежит на AB, N лежит на BC.
Требуется доказательство подобия треугольников ∆MBN и ∆ABC.
Посмотрев на ∆MBN и ∆ABC, видим, что угол В — общий, а отношение:
Отсюда делаем вывод, что ∆MBN ~ ∆ABC по II признаку подобия треугольников, что и требовалось доказать.
Примеры решения задач по геометрии на тему «Подобие треугольников»
_____________________________________________________________________
Беликова Ирина
Учитель физики, информатики и вычислительной техники. Победитель конкурса лучших учителей Российской Федерации в рамках Приоритетного Национального Проекта «Образование».
206. Мы знаем (п. 175), что если ∠A (чер. 203 или 204) пересечь двумя параллельными KL и BC, то отношение двух любых отрезков на одной стороне этого угла равно отношению двух соответствующих отрезков на другой (напр., AK/KB = AL/LC; AB/AK = AC/AL и т. д.). Но мы видим, что у нас получились еще отрезки на самих параллельных, а именно KL и BC. Возникает вопрос, нельзя ли из отрезков AL, LC и AC, лежащих на одной стороне нашего угла A, выбрать такие два, чтобы их отношение равнялось отношению отрезков KL и BC.
Для этой цели мы прежде всего отрезок KL перенесем на прямую BC, для чего надо построить LD || AB; тогда BD = KL. Тогда вместо отрезков KL и BC мы можем рассматривать отрезки BD и BC, которые расположены на стороне CB угла C. Так как ∠C оказался пересеченным двумя параллельными, а именно прямыми AB и LD, то, применяя п. 175 к углу C, мы найдем
BD/BC = AL/AC или KL/BC = AL/AC.
Вопрос решен: удалось найти два отрезка AL и AC на стороне AC так, что их отношение = KL/BC. Зная еще, что AK/AB = AL/AC, мы можем теперь написать равенства:
AK/AB = AL/AC = KL/BC.
Рассматривая эти равенства, мы приходим к заключению, что ими связаны стороны двух полученных треугольников, а именно ∆AKL и ∆ABC. Возникает новый вопрос: не связаны ли как-либо и углы этих треугольников?
На последний вопрос ответ легко найти: ∠A у наших треугольников общий, ∠K = ∠B, как соответственные при параллельных KL и BC и секущей AB, и ∠L = ∠C, как соответственные при тех же параллельных, но при секущей AC.
Мы можем перенести ∆AKL (чер. 203) в другое место, или, что тоже самое, построить новый ∆A’K’L’, равный ∆AKL; его стороны и углы будут соответственно равны сторонам и углам ∆AKL: AK = A’K’, AL = A’L’, KL = K’L’, ∠A = ∠A’, ∠K = ∠K’, ∠L = ∠L’.
Тогда мы получим ∆A’K’L’, находящийся в такой же зависимости с ∆ABC, как и ∆AKL:
1) у этих треугольников углы попарно равны: ∠A’ = ∠A, ∠K’ = ∠B, ∠L’ = ∠C;
2) для сторон имеем пропорции:
A’K’/AB = A’L’/AC = K’L’/BC (1)
Надо обратить внимание, что две стороны каждого отношения не случайно соединены в одно отношение, – нельзя, например, написать A’L’/AB = A’K’/BC = K’L’/AC. Надо уметь находить те стороны, которые должны быть членами одного отношения. Проще всего это сделать по углам треугольников: можно подметить, что стороны каждого отношения в равенствах (1) лежат в треугольниках против равных углов (A’K’ против ∠L и AB против равного этому угла C и т. д.). Принято называть те стороны, которые служат членами одного отношения, сходственными (сторона A’K’ сходна со стороною AB, A’L’ — с AC и K’L’ — с BC), причем сходственные стороны расположены в наших треугольниках против равных углов.
Равенство (1) можно прочесть сокращенно словами:
Стороны треугольника ∆A’K’L’ пропорциональны сходственным сторонам ∆ABC.
Слово «пропорциональны» означает: отношение одной пары сходственных сторон треугольников A’K’L’ и ABC равно отношению другой пары и равно отношению третьей пары.
Треугольники, обладающие двумя найденными выше признаками, называются подобными. Для обозначения подобия треугольников употребляют знак ~. Мы получили: ∆AKL ~ ∆ABC и также ∆A’K’L’ ~ ∆ABC.
Можно теперь установить:
Два треугольника называются подобными, если углы одного равны попарно углам другого и сходственные стороны их пропорциональны.
Замечание. Возьмем из равенства (1) лишь одно, например, A’K’/AB = A’L’/AC. Применяя сюда свойство п. 178, получим: A’K’/A’L’ = AB/AC, т. е. отношение двух сторон одного треугольника равно отношению двух сходственных сторон другого треугольника, подобного первому.
207. Основной признак подобия треугольников. Согласно предыдущему п., мы можем построить бесчисленное множество треугольников, подобных данному: для этого надо данный треугольник пересекать различными прямыми, параллельными одной из его сторон, и затем, если угодно, переносить каждый получаемый треугольник в другое место плоскости. Во всех получаемых треугольниках углы остаются неизменными, а отношение какой-либо стороны одного к сходственной стороне данного (масштаб подобия) меняется. Поэтому возникает мысль, недостаточно ли для подобия двух треугольников только равенства их углов.
Построим 2 треугольника: ∆ABC и ∆DEF (чер. 205) так, чтобы ∠A = ∠E и ∠B = ∠D. Тогда прежде всего находим, что ∠C = ∠F (ибо сумма углов каждого треугольника = 2d).
Наложим ∆DEF на ∆ABC так, чтобы, напр., точка E попала в точку A. Тогда вращением около этой точки можно достигнуть в силу равенства ∠E = ∠A того, чтобы ED и EF пошли соответственно по AB и AC; сторона DF должна занять такое положение KL, чтобы ∠AKL = ∠D = ∠B и ∠ALK = ∠F = ∠C, т. е., чтобы KL || BC, так как получаются равные соответственные углы.
Отсюда заключаем, что ∆DEF можно получить построением предыдущего п. и, следов., что ∆DEF ~ ∆ABC. Итак, если два угла одного треугольника равны соответственно двум углам другого, то эти треугольники подобны.
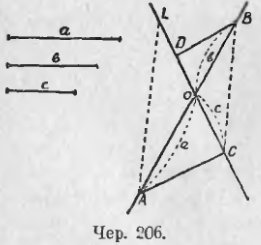
208. Задача. Построить четвертый пропорциональный к трем данным отрезкам.
Пусть даны отрезки a, b и c (чер. 206); требуется построить такой 4-й отрезок x, чтобы имела место пропорция a/b = c/x.
Строим две произвольных, пересекающихся в точке O, прямых AB и CD и откладываем от точки O на одной из них отрезки первого отношения: OA = a, OB = b (можно в одном, или в разных направлениях от точки O) и на другой прямой известный отрезок второго отношения OC = c. Затем соединим прямою концы тех отрезков, которые служат предыдущими членами нашей пропорции (если бы один из них не был известен, то надо соединить концы отрезков, служащих последующими членами данной пропорции); получим прямую AC, соединяющую концы отрезков a и c. Затем чрез точку B строим прямую BD || AC. Тогда поучим ∆OBD ~ ∆OAC (∠O = ∠O, как вертикальные и ∠C = ∠D, как внутренние накрест-лежащие, что достаточно по предыдущему п. для подобия наших треугольников). Отсюда имеем (п. 206) пропорциональность сходственных сторон:
OA/OB = OC/OD или a/b = c/OD,
отсюда вытекает, что искомый отрезок x = OD.
Если бы требовалось удовлетворить пропорции x/c = a/b, то надо было бы соединить точки B и C и через точку A построить AL || BD; тогда отрезок OL был бы искомым.
Замечание. Если мы построим отрезок x так, чтобы, напр., удовлетворилась пропорция x/c = a/b, то всякий другой отрезок x’ не удовлетворит этой пропорции; если x’ > x, то x’/c > x>c и, следовательно, x’/c > a/b, если x’ < x, то x’/c < x/c и x’/c < a/b.
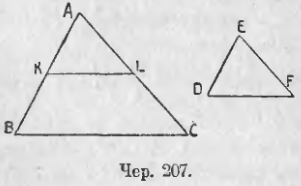
209. Другие признаки подобия треугольников. 1) Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между ними равны, то эти два треугольника подобны.
Пусть имеем ∆ABC (чер. 207); возьмем произвольный отрезок ED и построим, согласно п. 208, отрезок x так, чтобы имела место пропорция x/AC = ED/AB. Наконец, построим ∆EDF так чтобы у него одною стороною служил отрезок ED, другою стороною отрезок EF = x и, наконец, чтобы ∠E = ∠A. Тогда ∆EDF и ∆ABC связаны между собою соотношениями:
1) ∠E = ∠A и 2) EF/AC = ED/AB.
Подобны ли эти треугольники?
Для получения ответа на этот вопрос надо лишь заметить, что мы можем построить треугольник, равный ∆EDF, иным, более простым способом. Для этого отложим на стороне AB отрезок AK = ED и построим KL || BC; тогда ∆AKL ~ ∆ABC (п. 197) и, след., AL/AC = AK/AB.
Так как AK = ED и так как можно лишь одним способом (замечание п. 208) удовлетворить пропорции x/AC = ED/AB, то отсюда заключаем, что EF = AL и что ∆AKL = ∆EDF. Поэтому ∆EDF наложением можно совместить с ∆AKL и, следовательно, ∆EDF ~ ∆ABC. Этим оправдывается признак пропорциональности, изложенный в начале этого п.
2) Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны.
Пусть имеем ∆ABC (чер. 207); возьмем отрезок ED и построим согласно п. 208 два других отрезка x и y так, чтобы имели место пропорции: x/AC = ED/AB и y/BC = ED/AB. Построим затем по трем сторонам ED, x и y треугольник EDF (EF = x, DF = y).
Тогда ∆EDF и ∆ABC связаны между собою соотношениями:
1) EF/AC = ED/AB и 2) DF/BC = ED/AB
или, короче:
EF/AC = DF/BC = ED/AB.
Подобны ли эти треугольники?
Для решения этого вопроса заметим, что можно иным, более простым, способом построить треугольник, равный ∆EDF.
Для этого отложим на стороне AB отрезок AK = ED и построим KL || BC; тогда (п. 206) получим ∆AKL ~ ∆ABC и, след.,
AL/AC = KL/BC = AK/AB.
Так как отрезок AK = ED и так как, согласно замечанию п. 208, можно построить лишь один отрезок, удовлетворяющий пропорции x/AC = ED/AB, то заключаем, что AL = EF; также найдем, что KL = DF, откуда следует, что ∆EDF = ∆AKL, и наложением можно ∆EDF совместить с ∆AKL (иногда, может быть, придется для этого повернуть ∆EDF другою стороною). Поэтому ∆EDF ~ ∆ABC.
Этим оправдывается изложенный признак.
Подобным образом можно найти еще несколько признаков подобия, как вообще треугольников, так и каких-либо особых треугольников. Наприм., если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого, то эти треугольники подобны. Выяснение его справедливости основывается: 1) на замечании п. 208 и 2) на признаке равенства прямоугольных треугольников (п. 74, признак 4).
Замечание. В некоторых из следующих задач придется находить отношения отрезков, измеренных какою-либо единицею. Если, например, отрезок x = 7½ лин. един. и отрезок y = 3/10 лин. един. (линейная единица одна и та же), то, чтобы найти отношение отрезка x к отрезку y, надо выразить отрезок x числом, принимая за единицу отрезок y. Если y = 3/10 лин. единиц, то лин. един. = 10/3 * y и, следовательно,
x = (7½ * 10/3)y, откуда x/y = 7½ * 10/3 = 7½ : 3/10,
т. е. для наложения отношения отрезков, измеренных какою-либо одною единицею, надо найти отношение чисел, выражающих наши отрезки, а отношение чисел, как известно из арифметики, находится при помощи деления.
210. Упражнения.
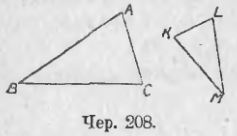
1. Даны 2 прямоугольных треугольника; острый угол одного из них = 41°, а острый угол другого = 49°. Узнать, подобны ли эти треугольники.
2. Даны ∆ABC и ∆KLM (чер. 208) так, что ∠B = ∠M и AB = 15 дм., BC = 18 дм., ML = 12 дм. и MK = 10 дм. Подобны ли эти треугольники? Если они подобны, то вычислить сторону AC, зная, что сторона KL = 5½ дм.
3. Даны ∆ABC и ∆KLM (чер. 208) так, что AB = 18 дм., BC = 20 дм., AC = 8 дм., KL = 6 дм., KM = 13½ дм., ML = 15 дм. Подобны ли эти треугольники? Как здесь узнать сходственные стороны?
4. В треугольниках ABC и KLM дано: AB = 16 дм., AC = 8 дм., BC = 20 дм., KL = 5 дм., MK = 10 дм. и ML = 12 дм. Подобны ли эти треугольники? Если не подобны, то как надо изменить сторону ML, чтобы треугольники оказались подобны?
5. Даны 2 подобных треугольника, стороны одного из которых равны соотв. 10, 14 и 16 дм. и большая сторона другого = 20 дм. Найти остальные 2 стороны второго треугольника.
6. Дан треугольник. Пользуясь способом п. 206, построить другой треугольник, подобный данному так, чтобы каждое отношение стороны нового треугольника к сходственной стороне второго было = ¾.
Сделать такое же построение, если вышеуказанное отношение должно равняться 2½.
211. Отношения высот и площадей подобных треугольников. Пусть имеем ∆ABC ~ ∆DEF (чер. 209). Следовательно, мы имеем: ∠A = ∠D, ∠B (∠ABC) = ∠E (∠DEF) и ∠C = ∠F (1) и
AB/DE = AC/DF = BC/EF (2)
Построим высоты BM и EN в наших треугольниках, опуская перпендикуляры на сходственные стороны; станем называть эти высоты сходственными. Тогда ∆ABM ~ ∆DEN, так как у них ∠A = ∠D на основании равенств (1) и ∠AMB = ∠DNE, как прямые углы (BM ⊥ AC и EN ⊥ DF), а этого достаточно для подобия наших треугольников (п. 207) и из их подобия получаем:
BM/EN = AB/DE.
На основании равенств (2) можем последнее равенство продолжить:
BM/EN = AB/DE = AC/DF = BC/EF,
т. е. отношение сходственных высот подобных треугольников равно отношению сходственных сторон.
Из ряда последних равных отношений обратим внимание на пропорцию.
BM/EN = AC/DF.
(Отношение сходственных высот = отношению оснований).
212. В п. 209 было указано, как находить отношение двух отрезков, измеренных одною и тою же единицею. Тоже относится и к нахождению отношения двух площадей, измеренных одною и тою же квадратною единицею: это отношение находится делением чисел, выражающих наши площади.
Мы будем в этом п., а равно во многих случаях и дальше под обозначением, например, AB понимать число, выражающее отрезок AB в каких-либо линейных единицах, также под обозначением «площадь ∆ABC» будем понимать число, выражающее площадь ∆ABC в квадратных единицах. При разборе одного вопроса все отрезки будут считаться измеренными одною и тою же линейною единицею, а все площади – соответствующими квадратными единицами.
Мы знаем (п. 201), что для измерения площади треугольника в квадратных единицах надо измерить его основание и высоту соответствующей линейною единицею и взять половину произведения полученных чисел.
Теперь, употребляя обозначение согласно вышесделанному условию, имеем для ∆ABC и ∆DEF (чер. 209)
площ. ∆ABC = (AC * BM) / 2 и площ. ∆DEF = (DF * EN) / 2.
Найдем отношение площадей наших треугольников делением
т. е. отношение площадей двух треугольников равно произведению отношения их оснований на отношение их высот.
Примем теперь во внимание, что мы имеем дело с подобными треугольниками — мы считаем, что ∆ABC ~ ∆DEF.
Тогда из предыдущего п. имеем:
BM/EN = AC/DF.
Заменяя в формуле, выражающей отношение площадей треугольников, отношение высот равным ему отношением оснований, получаем:
Можем также сказать, что это отношение = (AB/DE)2. Итак,
отношение площадей подобных треугольников равно квадрату отношения их сходственных сторон.
Этот результат согласуется с найденным в п. 160 (упражнения 5, 6 и 7).
Упражнение. Найти отношение площадей подобных треугольников, данных в п. 210 (упражнения 2, 3, 5 и 6).
213. Отношение площадей треугольников, имеющих по равному углу. Пусть в ∆ABC и ∆DEF (чер. 210) имеем ∠A = ∠D, а другие углы не равны. Тогда наши треугольники не подобны. Мы так же, как и в предыдущем п., построим высоты BM и EN этих треугольников и найдем делением отношение их площадей
Далее находим ∆ABC ~ ∆DEF (∠A = ∠D по условию и ∠M и ∠N прямые); следовательно:
BM/EN = AB/DE (2)
Но теперь уже нельзя заменить отношение высот (BM/EN) отношением оснований (AC/DF), так как эти треугольники не подобны. Пользуясь (2) из (1) имеем:
т. е. отношение площадей двух треугольников, имеющих по равному углу, равно произведению отношений сторон, составляющих эти углы.
Упражнение. Дан треугольник; построить другой треугольник так, чтобы один угол остался неизменным, а стороны, составляющие этот угол, увеличились одна в 2 раза и другая в 3 раза. Как увеличится его площадь? Ответ, легко находимый вычислением, желательно вычислить геометрически.
In Euclidean geometry, two objects are similar if they have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (enlarging or reducing), possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other.
|
|
|
|
|
For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other.
Figures shown in the same color are similar
If two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar. Corresponding sides of similar polygons are in proportion, and corresponding angles of similar polygons have the same measure.
Two congruent shapes are similar, with a scale factor of 1. However, some school textbooks specifically exclude congruent triangles from their definition of similar triangles by insisting that the sizes must be different if the triangles are to qualify as similar.[citation needed]
Similar triangles[edit]
Two triangles, △ABC and △A′B′C′, are similar if and only if corresponding angles have the same measure: this implies that they are similar if and only if the lengths of corresponding sides are proportional.[1] It can be shown that two triangles having congruent angles (equiangular triangles) are similar, that is, the corresponding sides can be proved to be proportional. This is known as the AAA similarity theorem.[2] Note that the «AAA» is a mnemonic: each one of the three A’s refers to an «angle». Due to this theorem, several authors simplify the definition of similar triangles to only require that the corresponding three angles are congruent.[3]
There are several criteria each of which is necessary and sufficient for two triangles to be similar:
- Any two pairs of congruent angles,[4] which in Euclidean geometry implies that their all three angles are congruent:[5]
-
- If ∠BAC is equal in measure to ∠B′A′C′, and ∠ABC is equal in measure to ∠A′B′C′, then this implies that ∠ACB is equal in measure to ∠A′C′B′ and the triangles are similar.
- All the corresponding sides are proportional:[6]
-
- AB/A′B′ = BC/B′C′ = AC/A′C′. This is equivalent to saying that one triangle (or its mirror image) is an enlargement of the other.
- Any two pairs of sides are proportional, and the angles included between these sides are congruent:[7]
-
- AB/A′B′ = BC/B′C′ and ∠ABC is equal in measure to ∠A′B′C′.
This is known as the SAS similarity criterion.[8] The «SAS» is a mnemonic: each one of the two S’s refers to a «side»; the A refers to an «angle» between the two sides.
Symbolically, we write the similarity and dissimilarity of two triangles△ABC and △A′B′C′ as follows:[9]
There are several elementary results concerning similar triangles in Euclidean geometry:[10]
- Any two equilateral triangles are similar.
- Two triangles, both similar to a third triangle, are similar to each other (transitivity of similarity of triangles).
- Corresponding altitudes of similar triangles have the same ratio as the corresponding sides.
- Two right triangles are similar if the hypotenuse and one other side have lengths in the same ratio.[11] There are several equivalent conditions in this case, such as the right triangles having an acute angle of the same measure, or having the lengths of the legs (sides) being in the same proportion.
Given a triangle △ABC and a line segment DE one can, with ruler and compass, find a point F such that △ABC ∼ △DEF. The statement that the point F satisfying this condition exists is Wallis’s postulate[12] and is logically equivalent to Euclid’s parallel postulate.[13] In hyperbolic geometry (where Wallis’s postulate is false) similar triangles are congruent.
In the axiomatic treatment of Euclidean geometry given by George David Birkhoff (see Birkhoff’s axioms) the SAS similarity criterion given above was used to replace both Euclid’s parallel postulate and the SAS axiom which enabled the dramatic shortening of Hilbert’s axioms.[8]
Similar triangles provide the basis for many synthetic (without the use of coordinates) proofs in Euclidean geometry. Among the elementary results that can be proved this way are: the angle bisector theorem, the geometric mean theorem, Ceva’s theorem, Menelaus’s theorem and the Pythagorean theorem. Similar triangles also provide the foundations for right triangle trigonometry.[14]
Other similar polygons[edit]
The concept of similarity extends to polygons with more than three sides. Given any two similar polygons, corresponding sides taken in the same sequence (even if clockwise for one polygon and counterclockwise for the other) are proportional and corresponding angles taken in the same sequence are equal in measure. However, proportionality of corresponding sides is not by itself sufficient to prove similarity for polygons beyond triangles (otherwise, for example, all rhombi would be similar). Likewise, equality of all angles in sequence is not sufficient to guarantee similarity (otherwise all rectangles would be similar). A sufficient condition for similarity of polygons is that corresponding sides and diagonals are proportional.
For given n, all regular n-gons are similar.
Similar curves[edit]
Several types of curves have the property that all examples of that type are similar to each other. These include:
- Lines (any two lines are even congruent)
- Line segments
- Circles
- Parabolas[15]
- Hyperbolas of a specific eccentricity[16]
- Ellipses of a specific eccentricity[16]
- Catenaries
- Graphs of the logarithm function for different bases
- Graphs of the exponential function for different bases
- Logarithmic spirals are self-similar
In Euclidean space[edit]
A similarity (also called a similarity transformation or similitude) of a Euclidean space is a bijection f from the space onto itself that multiplies all distances by the same positive real number r, so that for any two points x and y we have
where «d(x,y)» is the Euclidean distance from x to y.[17] The scalar r has many names in the literature including; the ratio of similarity, the stretching factor and the similarity coefficient. When r = 1 a similarity is called an isometry (rigid transformation). Two sets are called similar if one is the image of the other under a similarity.
As a map f : ℝn → ℝn, a similarity of ratio r takes the form
where A ∈ On(ℝ) is an n × n orthogonal matrix and t ∈ ℝn is a translation vector.
Similarities preserve planes, lines, perpendicularity, parallelism, midpoints, inequalities between distances and line segments.[18] Similarities preserve angles but do not necessarily preserve orientation, direct similitudes preserve orientation and opposite similitudes change it.[19]
The similarities of Euclidean space form a group under the operation of composition called the similarities group S.[20] The direct similitudes form a normal subgroup of S and the Euclidean group E(n) of isometries also forms a normal subgroup.[21] The similarities group S is itself a subgroup of the affine group, so every similarity is an affine transformation.
One can view the Euclidean plane as the complex plane,[22] that is, as a 2-dimensional space over the reals. The 2D similarity transformations can then be expressed in terms of complex arithmetic and are given by f(z) = az + b (direct similitudes) and f(z) = az + b (opposite similitudes), where a and b are complex numbers, a ≠ 0. When |a| = 1, these similarities are isometries.
Area ratio and volume ratio[edit]
The tessellation of the large triangle shows that it is similar to the small triangle with an area ratio of 5. The similarity ratio is 5/h = h/1 = √5. This can be used to construct a non-periodic infinite tiling.
The ratio between the areas of similar figures is equal to the square of the ratio of corresponding lengths of those figures (for example, when the side of a square or the radius of a circle is multiplied by three, its area is multiplied by nine — i.e. by three squared). The altitudes of similar triangles are in the same ratio as corresponding sides. If a triangle has a side of length b and an altitude drawn to that side of length h then a similar triangle with corresponding side of length kb will have an altitude drawn to that side of length kh. The area of the first triangle is, A = 1/2bh, while the area of the similar triangle will be A′ = 1/2(kb)(kh) = k2A. Similar figures which can be decomposed into similar triangles will have areas related in the same way. The relationship holds for figures that are not rectifiable as well.
The ratio between the volumes of similar figures is equal to the cube of the ratio of corresponding lengths of those figures (for example, when the edge of a cube or the radius of a sphere is multiplied by three, its volume is multiplied by 27 — i.e. by three cubed).
Galileo’s square–cube law concerns similar solids. If the ratio of similitude (ratio of corresponding sides) between the solids is k, then the ratio of surface areas of the solids will be k2, while the ratio of volumes will be k3.
Similarity with a center[edit]
Example where each similarity
composed with itself several times successively
has a center at the center of a regular polygon that it shrinks.
Example of direct similarity of center S
decomposed into a rotation of 135° angle
and a homothety that halves areas.
Examples of direct similarities that have each a center.
If a similarity has exactly one invariant point: a point that the similarity keeps unchanged, then this only point is called «center» of the similarity.
On the first image below the title, on the left, one or another similarity shrinks a regular polygon into a concentric one, the vertices of which are each on a side of the previous polygon. This rotational reduction is repeated, so the initial polygon is extended into an abyss of regular polygons. The center of the similarity is the common center of the successive polygons. A red segment joins a vertex of the initial polygon to its image under the similarity, followed by a red segment going to the following image of vertex, and so on to form a spiral. Actually we can see more than three direct similarities on this first image, because every regular polygon is invariant under certain direct similarities, more precisely certain rotations the center of which is the center of the polygon, and a composition of direct similarities is also a direct similarity. For example we see the image of the initial regular pentagon under a homothety of negative 

Below the title on the right, the second image shows a similarity decomposed into a rotation and a homothety. Similarity and rotation have the same angle of +135 degrees modulo 360 degrees. Similarity and homothety have the same ratio 



This direct similarity that transforms triangle EFA into triangle ATB can be decomposed into a rotation and a homothety of same center S in several manners. For example, 



With 








How to construct the center S of direct similarity 




In general metric spaces[edit]
In a general metric space (X, d), an exact similitude is a function f from the metric space X into itself that multiplies all distances by the same positive scalar r, called f ‘s contraction factor, so that for any two points x and y we have
Weaker versions of similarity would for instance have f be a bi-Lipschitz function and the scalar r a limit
This weaker version applies when the metric is an effective resistance on a topologically self-similar set.
A self-similar subset of a metric space (X, d) is a set K for which there exists a finite set of similitudes { fs }s∈S with contraction factors 0 ≤ rs < 1 such that K is the unique compact subset of X for which
-
A self-similar set constructed with two similitudes z’=0.1[(4+i)z+4] and z’=0.1[(4+7i)z*+5-2i]
These self-similar sets have a self-similar measure μD with dimension D given by the formula
which is often (but not always) equal to the set’s Hausdorff dimension and packing dimension. If the overlaps between the fs(K) are «small», we have the following simple formula for the measure:
Topology[edit]
In topology, a metric space can be constructed by defining a similarity instead of a distance. The similarity is a function such that its value is greater when two points are closer (contrary to the distance, which is a measure of dissimilarity: the closer the points, the lesser the distance).
The definition of the similarity can vary among authors, depending on which properties are desired. The basic common properties are
- Positive defined:
- Majored by the similarity of one element on itself (auto-similarity):
More properties can be invoked, such as reflectivity (

Note that, in the topological sense used here, a similarity is a kind of measure. This usage is not the same as the similarity transformation of the § In Euclidean space and § In general metric spaces sections of this article.
Self-similarity[edit]
Self-similarity means that a pattern is non-trivially similar to itself, e.g., the set {…, 0.5, 0.75, 1, 1.5, 2, 3, 4, 6, 8, 12, …} of numbers of the form {2i, 3·2i} where i ranges over all integers. When this set is plotted on a logarithmic scale it has one-dimensional translational symmetry: adding or subtracting the logarithm of two to the logarithm of one of these numbers produces the logarithm of another of these numbers. In the given set of numbers themselves, this corresponds to a similarity transformation in which the numbers are multiplied or divided by two.
Psychology[edit]
|
This section needs expansion. You can help by adding to it. (July 2021) |
The intuition for the notion of geometric similarity already appears in human children, as can be seen in their drawings.[23]
See also[edit]
- Congruence (geometry)
- Hamming distance (string or sequence similarity)
- Helmert transformation
- Inversive geometry
- Jaccard index
- Proportionality
- Basic proportionality theorem
- Semantic similarity
- Similarity search
- Similarity (philosophy)
- Similarity space on numerical taxonomy
- Homoeoid (shell of concentric, similar ellipsoids)
- Solution of triangles
Notes[edit]
- ^ Sibley 1998, p. 35.
- ^ Stahl 2003, p. 127. This is also proved in Euclid’s Elements, Book VI, Proposition 4.
- ^ For instance, Venema 2006, p. 122 and Henderson & Taimiņa 2005, p. 123.
- ^ Euclid’s Elements, Book VI, Proposition 4.
- ^ This statement is not true in non-Euclidean geometry where the triangle angle sum is not 180 degrees.
- ^ Euclid’s Elements, Book VI, Proposition 5.
- ^ Euclid’s Elements, Book VI, Proposition 6.
- ^ a b Venema 2006, p. 143.
- ^ Posamentier, Alfred S.; Lehmann, Ingmar (2012). The Secrets of Triangles. Prometheus Books. p. 22.
- ^ Jacobs 1974, pp. 384–393.
- ^ Hadamard, Jacques (2008). Lessons in Geometry, Vol. I: Plane Geometry. American Mathematical Society. Theorem 120, p. 125. ISBN 978-0-8218-4367-3.
- ^ Named for John Wallis (1616–1703)
- ^ Venema 2006, p. 122.
- ^ Venema 2006, p. 145.
- ^ a proof from academia.edu
- ^ a b The shape of an ellipse or hyperbola depends only on the ratio b/a
- ^ Smart 1998, p. 92.
- ^ Yale 1968, p. 47 Theorem 2.1.
- ^ Pedoe 1988, pp. 179–181.
- ^ Yale 1968, p. 46.
- ^ Pedoe 1988, p. 182.
- ^ This traditional term, as explained in its article, is a misnomer. This is actually the 1-dimensional complex line.
- ^ Cox, Dana Christine (2008). Understanding Similarity: Bridging Geometric and Numeric Contexts for Proportional Reasoning (Ph.D.). Kalamazoo, Michigan: Western Michigan University. ISBN 978-0-549-75657-6. S2CID 61331653.
References[edit]
- Henderson, David W.; Taimiņa, Daina (2005). Experiencing Geometry/Euclidean and Non-Euclidean with History (3rd ed.). Pearson Prentice-Hall. ISBN 978-0-13-143748-7.
- Jacobs, Harold R. (1974). Geometry. W. H. Freeman and Co. ISBN 0-7167-0456-0.
- Pedoe, Dan (1988) [1970]. Geometry/A Comprehensive Course. Dover. ISBN 0-486-65812-0.
- Sibley, Thomas Q. (1998). The Geometric Viewpoint/A Survey of Geometries. Addison-Wesley. ISBN 978-0-201-87450-1.
- Smart, James R. (1998). Modern Geometries (5th ed.). Brooks/Cole. ISBN 0-534-35188-3.
- Stahl, Saul (2003). Geometry/From Euclid to Knots. Prentice-Hall. ISBN 978-0-13-032927-1.
- Venema, Gerard A. (2006). Foundations of Geometry. Pearson Prentice-Hall. ISBN 978-0-13-143700-5.
- Yale, Paul B. (1968). Geometry and Symmetry. Holden-Day.
Further reading[edit]
- Cederberg, Judith N. (2001) [1989]. «Chapter 3.12: Similarity Transformations». A Course in Modern Geometries. Springer. pp. 183–189. ISBN 0-387-98972-2.
- Coxeter, H. S. M. (1969) [1961]. «§5 Similarity in the Euclidean Plane». pp. 67–76. «§7 Isometry and Similarity in Euclidean Space». pp. 96–104. Introduction to Geometry. John Wiley & Sons.
- Ewald, Günter (1971). Geometry: An Introduction. Wadsworth Publishing. pp. 106, 181.
- Martin, George E. (1982). «Chapter 13: Similarities in the Plane». Transformation Geometry: An Introduction to Symmetry. Springer. pp. 136–146. ISBN 0-387-90636-3.
External links[edit]
- Animated demonstration of similar triangles
In Euclidean geometry, two objects are similar if they have the same shape, or one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (enlarging or reducing), possibly with additional translation, rotation and reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruent to the result of a particular uniform scaling of the other.
|
|
|
|
|
For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other.
Figures shown in the same color are similar
If two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar. Corresponding sides of similar polygons are in proportion, and corresponding angles of similar polygons have the same measure.
Two congruent shapes are similar, with a scale factor of 1. However, some school textbooks specifically exclude congruent triangles from their definition of similar triangles by insisting that the sizes must be different if the triangles are to qualify as similar.[citation needed]
Similar triangles[edit]
Two triangles, △ABC and △A′B′C′, are similar if and only if corresponding angles have the same measure: this implies that they are similar if and only if the lengths of corresponding sides are proportional.[1] It can be shown that two triangles having congruent angles (equiangular triangles) are similar, that is, the corresponding sides can be proved to be proportional. This is known as the AAA similarity theorem.[2] Note that the «AAA» is a mnemonic: each one of the three A’s refers to an «angle». Due to this theorem, several authors simplify the definition of similar triangles to only require that the corresponding three angles are congruent.[3]
There are several criteria each of which is necessary and sufficient for two triangles to be similar:
- Any two pairs of congruent angles,[4] which in Euclidean geometry implies that their all three angles are congruent:[5]
-
- If ∠BAC is equal in measure to ∠B′A′C′, and ∠ABC is equal in measure to ∠A′B′C′, then this implies that ∠ACB is equal in measure to ∠A′C′B′ and the triangles are similar.
- All the corresponding sides are proportional:[6]
-
- AB/A′B′ = BC/B′C′ = AC/A′C′. This is equivalent to saying that one triangle (or its mirror image) is an enlargement of the other.
- Any two pairs of sides are proportional, and the angles included between these sides are congruent:[7]
-
- AB/A′B′ = BC/B′C′ and ∠ABC is equal in measure to ∠A′B′C′.
This is known as the SAS similarity criterion.[8] The «SAS» is a mnemonic: each one of the two S’s refers to a «side»; the A refers to an «angle» between the two sides.
Symbolically, we write the similarity and dissimilarity of two triangles△ABC and △A′B′C′ as follows:[9]
There are several elementary results concerning similar triangles in Euclidean geometry:[10]
- Any two equilateral triangles are similar.
- Two triangles, both similar to a third triangle, are similar to each other (transitivity of similarity of triangles).
- Corresponding altitudes of similar triangles have the same ratio as the corresponding sides.
- Two right triangles are similar if the hypotenuse and one other side have lengths in the same ratio.[11] There are several equivalent conditions in this case, such as the right triangles having an acute angle of the same measure, or having the lengths of the legs (sides) being in the same proportion.
Given a triangle △ABC and a line segment DE one can, with ruler and compass, find a point F such that △ABC ∼ △DEF. The statement that the point F satisfying this condition exists is Wallis’s postulate[12] and is logically equivalent to Euclid’s parallel postulate.[13] In hyperbolic geometry (where Wallis’s postulate is false) similar triangles are congruent.
In the axiomatic treatment of Euclidean geometry given by George David Birkhoff (see Birkhoff’s axioms) the SAS similarity criterion given above was used to replace both Euclid’s parallel postulate and the SAS axiom which enabled the dramatic shortening of Hilbert’s axioms.[8]
Similar triangles provide the basis for many synthetic (without the use of coordinates) proofs in Euclidean geometry. Among the elementary results that can be proved this way are: the angle bisector theorem, the geometric mean theorem, Ceva’s theorem, Menelaus’s theorem and the Pythagorean theorem. Similar triangles also provide the foundations for right triangle trigonometry.[14]
Other similar polygons[edit]
The concept of similarity extends to polygons with more than three sides. Given any two similar polygons, corresponding sides taken in the same sequence (even if clockwise for one polygon and counterclockwise for the other) are proportional and corresponding angles taken in the same sequence are equal in measure. However, proportionality of corresponding sides is not by itself sufficient to prove similarity for polygons beyond triangles (otherwise, for example, all rhombi would be similar). Likewise, equality of all angles in sequence is not sufficient to guarantee similarity (otherwise all rectangles would be similar). A sufficient condition for similarity of polygons is that corresponding sides and diagonals are proportional.
For given n, all regular n-gons are similar.
Similar curves[edit]
Several types of curves have the property that all examples of that type are similar to each other. These include:
- Lines (any two lines are even congruent)
- Line segments
- Circles
- Parabolas[15]
- Hyperbolas of a specific eccentricity[16]
- Ellipses of a specific eccentricity[16]
- Catenaries
- Graphs of the logarithm function for different bases
- Graphs of the exponential function for different bases
- Logarithmic spirals are self-similar
In Euclidean space[edit]
A similarity (also called a similarity transformation or similitude) of a Euclidean space is a bijection f from the space onto itself that multiplies all distances by the same positive real number r, so that for any two points x and y we have
where «d(x,y)» is the Euclidean distance from x to y.[17] The scalar r has many names in the literature including; the ratio of similarity, the stretching factor and the similarity coefficient. When r = 1 a similarity is called an isometry (rigid transformation). Two sets are called similar if one is the image of the other under a similarity.
As a map f : ℝn → ℝn, a similarity of ratio r takes the form
where A ∈ On(ℝ) is an n × n orthogonal matrix and t ∈ ℝn is a translation vector.
Similarities preserve planes, lines, perpendicularity, parallelism, midpoints, inequalities between distances and line segments.[18] Similarities preserve angles but do not necessarily preserve orientation, direct similitudes preserve orientation and opposite similitudes change it.[19]
The similarities of Euclidean space form a group under the operation of composition called the similarities group S.[20] The direct similitudes form a normal subgroup of S and the Euclidean group E(n) of isometries also forms a normal subgroup.[21] The similarities group S is itself a subgroup of the affine group, so every similarity is an affine transformation.
One can view the Euclidean plane as the complex plane,[22] that is, as a 2-dimensional space over the reals. The 2D similarity transformations can then be expressed in terms of complex arithmetic and are given by f(z) = az + b (direct similitudes) and f(z) = az + b (opposite similitudes), where a and b are complex numbers, a ≠ 0. When |a| = 1, these similarities are isometries.
Area ratio and volume ratio[edit]
The tessellation of the large triangle shows that it is similar to the small triangle with an area ratio of 5. The similarity ratio is 5/h = h/1 = √5. This can be used to construct a non-periodic infinite tiling.
The ratio between the areas of similar figures is equal to the square of the ratio of corresponding lengths of those figures (for example, when the side of a square or the radius of a circle is multiplied by three, its area is multiplied by nine — i.e. by three squared). The altitudes of similar triangles are in the same ratio as corresponding sides. If a triangle has a side of length b and an altitude drawn to that side of length h then a similar triangle with corresponding side of length kb will have an altitude drawn to that side of length kh. The area of the first triangle is, A = 1/2bh, while the area of the similar triangle will be A′ = 1/2(kb)(kh) = k2A. Similar figures which can be decomposed into similar triangles will have areas related in the same way. The relationship holds for figures that are not rectifiable as well.
The ratio between the volumes of similar figures is equal to the cube of the ratio of corresponding lengths of those figures (for example, when the edge of a cube or the radius of a sphere is multiplied by three, its volume is multiplied by 27 — i.e. by three cubed).
Galileo’s square–cube law concerns similar solids. If the ratio of similitude (ratio of corresponding sides) between the solids is k, then the ratio of surface areas of the solids will be k2, while the ratio of volumes will be k3.
Similarity with a center[edit]
Example where each similarity
composed with itself several times successively
has a center at the center of a regular polygon that it shrinks.
Example of direct similarity of center S
decomposed into a rotation of 135° angle
and a homothety that halves areas.
Examples of direct similarities that have each a center.
If a similarity has exactly one invariant point: a point that the similarity keeps unchanged, then this only point is called «center» of the similarity.
On the first image below the title, on the left, one or another similarity shrinks a regular polygon into a concentric one, the vertices of which are each on a side of the previous polygon. This rotational reduction is repeated, so the initial polygon is extended into an abyss of regular polygons. The center of the similarity is the common center of the successive polygons. A red segment joins a vertex of the initial polygon to its image under the similarity, followed by a red segment going to the following image of vertex, and so on to form a spiral. Actually we can see more than three direct similarities on this first image, because every regular polygon is invariant under certain direct similarities, more precisely certain rotations the center of which is the center of the polygon, and a composition of direct similarities is also a direct similarity. For example we see the image of the initial regular pentagon under a homothety of negative 

Below the title on the right, the second image shows a similarity decomposed into a rotation and a homothety. Similarity and rotation have the same angle of +135 degrees modulo 360 degrees. Similarity and homothety have the same ratio 



This direct similarity that transforms triangle EFA into triangle ATB can be decomposed into a rotation and a homothety of same center S in several manners. For example, 



With 








How to construct the center S of direct similarity 




In general metric spaces[edit]
In a general metric space (X, d), an exact similitude is a function f from the metric space X into itself that multiplies all distances by the same positive scalar r, called f ‘s contraction factor, so that for any two points x and y we have
Weaker versions of similarity would for instance have f be a bi-Lipschitz function and the scalar r a limit
This weaker version applies when the metric is an effective resistance on a topologically self-similar set.
A self-similar subset of a metric space (X, d) is a set K for which there exists a finite set of similitudes { fs }s∈S with contraction factors 0 ≤ rs < 1 such that K is the unique compact subset of X for which
-
A self-similar set constructed with two similitudes z’=0.1[(4+i)z+4] and z’=0.1[(4+7i)z*+5-2i]
These self-similar sets have a self-similar measure μD with dimension D given by the formula
which is often (but not always) equal to the set’s Hausdorff dimension and packing dimension. If the overlaps between the fs(K) are «small», we have the following simple formula for the measure:
Topology[edit]
In topology, a metric space can be constructed by defining a similarity instead of a distance. The similarity is a function such that its value is greater when two points are closer (contrary to the distance, which is a measure of dissimilarity: the closer the points, the lesser the distance).
The definition of the similarity can vary among authors, depending on which properties are desired. The basic common properties are
- Positive defined:
- Majored by the similarity of one element on itself (auto-similarity):
More properties can be invoked, such as reflectivity (

Note that, in the topological sense used here, a similarity is a kind of measure. This usage is not the same as the similarity transformation of the § In Euclidean space and § In general metric spaces sections of this article.
Self-similarity[edit]
Self-similarity means that a pattern is non-trivially similar to itself, e.g., the set {…, 0.5, 0.75, 1, 1.5, 2, 3, 4, 6, 8, 12, …} of numbers of the form {2i, 3·2i} where i ranges over all integers. When this set is plotted on a logarithmic scale it has one-dimensional translational symmetry: adding or subtracting the logarithm of two to the logarithm of one of these numbers produces the logarithm of another of these numbers. In the given set of numbers themselves, this corresponds to a similarity transformation in which the numbers are multiplied or divided by two.
Psychology[edit]
|
This section needs expansion. You can help by adding to it. (July 2021) |
The intuition for the notion of geometric similarity already appears in human children, as can be seen in their drawings.[23]
See also[edit]
- Congruence (geometry)
- Hamming distance (string or sequence similarity)
- Helmert transformation
- Inversive geometry
- Jaccard index
- Proportionality
- Basic proportionality theorem
- Semantic similarity
- Similarity search
- Similarity (philosophy)
- Similarity space on numerical taxonomy
- Homoeoid (shell of concentric, similar ellipsoids)
- Solution of triangles
Notes[edit]
- ^ Sibley 1998, p. 35.
- ^ Stahl 2003, p. 127. This is also proved in Euclid’s Elements, Book VI, Proposition 4.
- ^ For instance, Venema 2006, p. 122 and Henderson & Taimiņa 2005, p. 123.
- ^ Euclid’s Elements, Book VI, Proposition 4.
- ^ This statement is not true in non-Euclidean geometry where the triangle angle sum is not 180 degrees.
- ^ Euclid’s Elements, Book VI, Proposition 5.
- ^ Euclid’s Elements, Book VI, Proposition 6.
- ^ a b Venema 2006, p. 143.
- ^ Posamentier, Alfred S.; Lehmann, Ingmar (2012). The Secrets of Triangles. Prometheus Books. p. 22.
- ^ Jacobs 1974, pp. 384–393.
- ^ Hadamard, Jacques (2008). Lessons in Geometry, Vol. I: Plane Geometry. American Mathematical Society. Theorem 120, p. 125. ISBN 978-0-8218-4367-3.
- ^ Named for John Wallis (1616–1703)
- ^ Venema 2006, p. 122.
- ^ Venema 2006, p. 145.
- ^ a proof from academia.edu
- ^ a b The shape of an ellipse or hyperbola depends only on the ratio b/a
- ^ Smart 1998, p. 92.
- ^ Yale 1968, p. 47 Theorem 2.1.
- ^ Pedoe 1988, pp. 179–181.
- ^ Yale 1968, p. 46.
- ^ Pedoe 1988, p. 182.
- ^ This traditional term, as explained in its article, is a misnomer. This is actually the 1-dimensional complex line.
- ^ Cox, Dana Christine (2008). Understanding Similarity: Bridging Geometric and Numeric Contexts for Proportional Reasoning (Ph.D.). Kalamazoo, Michigan: Western Michigan University. ISBN 978-0-549-75657-6. S2CID 61331653.
References[edit]
- Henderson, David W.; Taimiņa, Daina (2005). Experiencing Geometry/Euclidean and Non-Euclidean with History (3rd ed.). Pearson Prentice-Hall. ISBN 978-0-13-143748-7.
- Jacobs, Harold R. (1974). Geometry. W. H. Freeman and Co. ISBN 0-7167-0456-0.
- Pedoe, Dan (1988) [1970]. Geometry/A Comprehensive Course. Dover. ISBN 0-486-65812-0.
- Sibley, Thomas Q. (1998). The Geometric Viewpoint/A Survey of Geometries. Addison-Wesley. ISBN 978-0-201-87450-1.
- Smart, James R. (1998). Modern Geometries (5th ed.). Brooks/Cole. ISBN 0-534-35188-3.
- Stahl, Saul (2003). Geometry/From Euclid to Knots. Prentice-Hall. ISBN 978-0-13-032927-1.
- Venema, Gerard A. (2006). Foundations of Geometry. Pearson Prentice-Hall. ISBN 978-0-13-143700-5.
- Yale, Paul B. (1968). Geometry and Symmetry. Holden-Day.
Further reading[edit]
- Cederberg, Judith N. (2001) [1989]. «Chapter 3.12: Similarity Transformations». A Course in Modern Geometries. Springer. pp. 183–189. ISBN 0-387-98972-2.
- Coxeter, H. S. M. (1969) [1961]. «§5 Similarity in the Euclidean Plane». pp. 67–76. «§7 Isometry and Similarity in Euclidean Space». pp. 96–104. Introduction to Geometry. John Wiley & Sons.
- Ewald, Günter (1971). Geometry: An Introduction. Wadsworth Publishing. pp. 106, 181.
- Martin, George E. (1982). «Chapter 13: Similarities in the Plane». Transformation Geometry: An Introduction to Symmetry. Springer. pp. 136–146. ISBN 0-387-90636-3.
External links[edit]
- Animated demonstration of similar triangles